Descrição
Estudo das vigas biapoiadas sob carregamento, descrição da geometria das vigas e dos carregamentos possíveis, conceitos dos efeitos internos, esforço cortante V e momento fletor M, modelagem computacional das vigas biapoiadas.
PROPÓSITO
Compreender, por meio das equações de equilíbrio da estática, as reações nos dois apoios da viga isostática, bem como os efeitos da flexão e do cisalhamento.
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta, uma calculadora científica ou a de seu smartphone/computador, além de um software para auxiliar a traçar os diagramas de esforço cortante e de momento fletor.
OBJETIVOS
Módulo 1
Identificar a geometria e os carregamentos de uma viga biapoiada isostática
Módulo 2
Calcular os efeitos internos de flexão e cisalhamento numa viga biapoiada isostática
Módulo 3
Esquematizar os diagramas de estado de vigas biapoiadas isostáticas
Módulo 4
Compreender a modelagem computacional das vigas biapoiadas isostáticas
BEM-VINDO AO ESTUDO SOBRE A IMPORTÂNCIA DAS VIGAS NAS ESTRUTURAS
MÓDULO 1
Identificar a geometria e os carregamentos de uma viga biapoiada isostática
Introdução
Uma viga é um elemento estrutural prismático de uma grande estrutura que suporta carregamentos externos.
Em função do tipo de carregamento sobre a viga, vários são os efeitos internos possíveis:
- O esforço cortante ou cisalhante.
- A flexão.
- A torção.
- O esforço normal.
As vigas podem estar vinculadas de diversas maneiras. Algumas dessas possibilidades estão mostradas na figura.
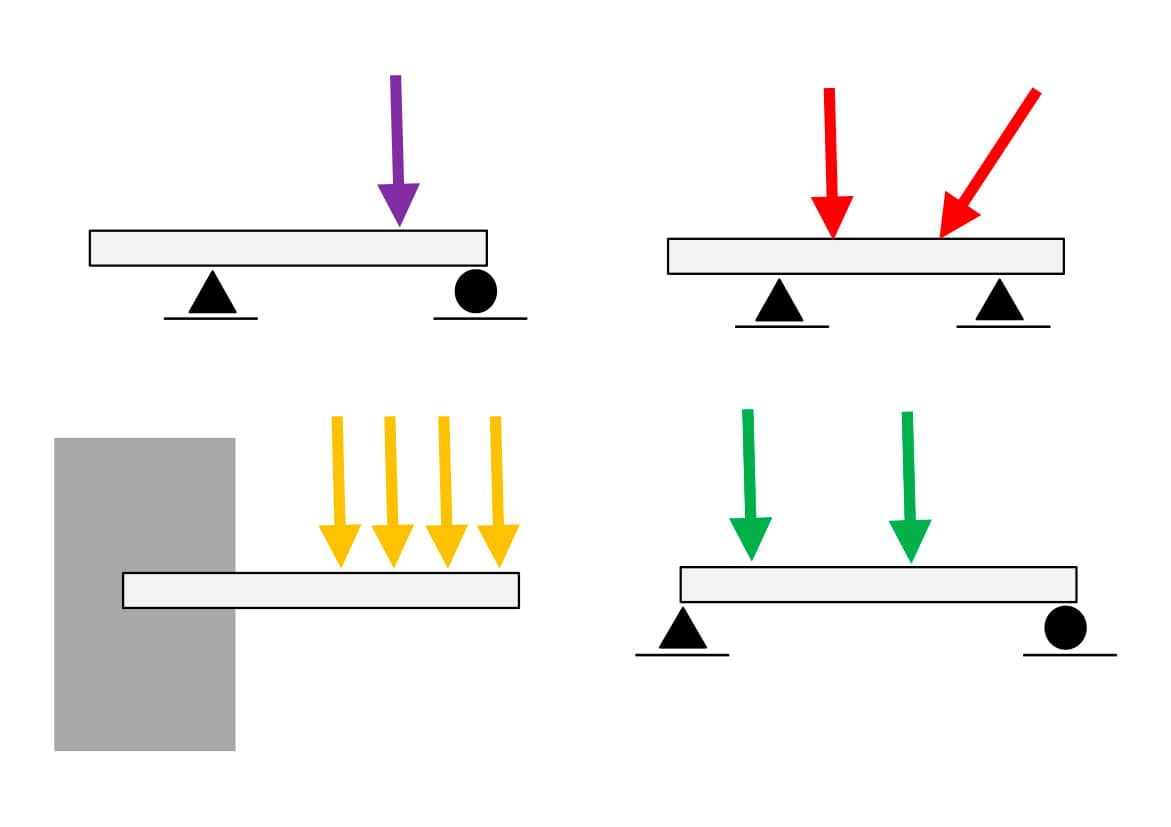
Vigas vinculadas de formas distintas. Fonte: o autor.
Neste tema, serão estudadas particularmente as vigas biapoiadas isostáticas.
São vigas que se encontram vinculadas a dois apoios sendo um do primeiro gênero e o outro de segundo gênero. Elas podem estar ou não em balanço, conforme ilustra a figura a seguir.
Vigas biapoiadas isostáticas. Fonte: O autor.
Nesta fase introdutória do tema, será feita uma abordagem bastante simples a respeito da estaticidade das vigas biapoiadas. Elas podem ser:
As vigas hipostáticas (apoiadas sobre dois roletes, por exemplo), sob determinada condição de carregamento, podem não manter o equilíbrio.
As isostáticas estão vinculadas de tal forma que três são as reações de apoio que podem ser determinadas utilizando apenas as três equações do equilíbrio estático
As hiperestáticas apresentam mais que três reações de apoio, necessitando, portanto, de equações auxiliares (de deformação, por exemplo).
Na figura, a seguir, são apresentadas algumas dessas vigas.

Vigas hipostáticas, isostáticas e hiperestáticas. Fonte: O autor.
Geometria e os carregamentos de uma viga biapoiada
No item anterior, a viga foi descrita como um elemento estrutural prismático.
De maneira bem coloquial, as vigas são elementos de grande comprimento, vinculadas a apoios, que resistem a carregamentos externos.
Há uma gama de possibilidades para as seções retas das vigas. Podem ser constantes ou variáveis ao longo do comprimento L da barra (viga).
Seções comuns na Engenharia são as retangulares (quadradas), em forma de I, em forma de T, em forma de C, circulares etc.
Ademais, o tipo de material também apresenta um grande espectro. Podem ser de metais, de madeira, de concreto etc.
Comentário
A escolha da forma geométrica e do material da viga será estudada em disciplinas posteriores.
A figura seguinte apresenta algumas possibilidades citadas, em que a_a’ e b_b’ são os cortes.
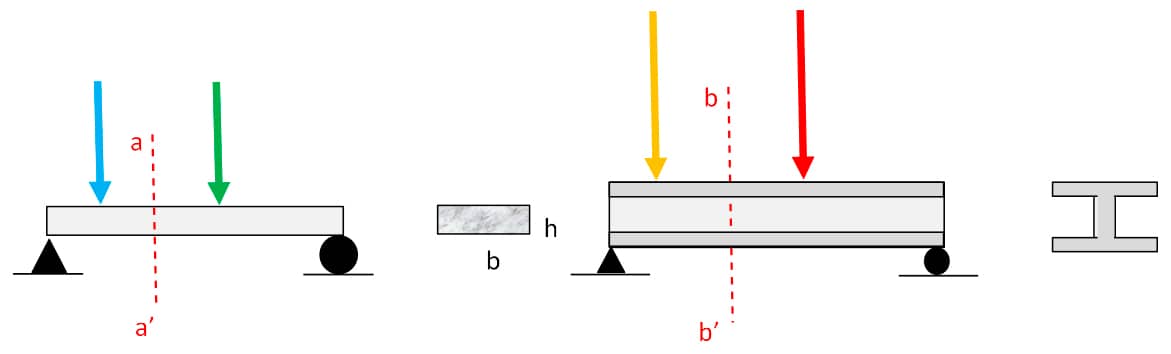
Seções retas de vigas: retangular e “em I”. Fonte: O autor.
Em relação ao carregamento que as vigas biapoiadas podem estar submetidas, existem dois grandes grupos: concentrado e distribuído. Cada um deles pode ser associado à força (carga) ou carga momento.
Devemos ter em mente que as várias partes de uma grande estrutura se vinculam de alguma forma.
Exemplo
Uma viga de um prédio pode estar sendo o apoio transversal de outras duas ou três vigas.
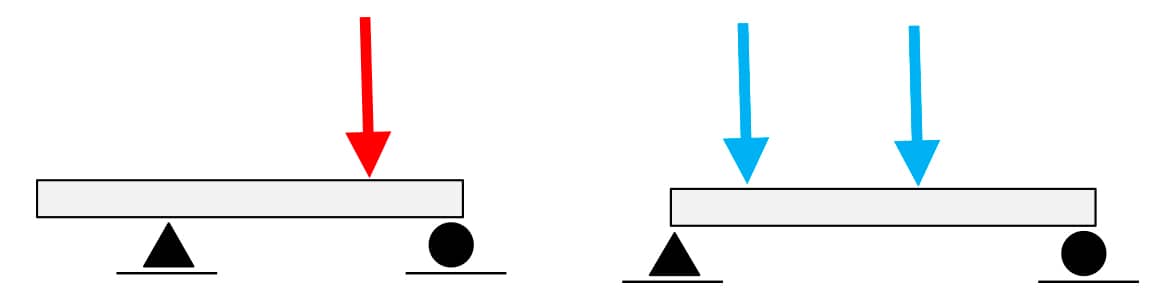
Anteriormente, já foi feita uma abordagem em que se mostrou a diferença entre os conceitos de força concentrada e de força distribuída.
concentrada
No caso da força concentrada, o ponto de sua aplicação é único, mas a linha de ação pode ser qualquer uma. Linha de ação vertical à viga é bastante comum. Perceba, porém, que na primeira figura do módulo, existe uma situação em que a força concentrada tem linha de ação oblíqua em relação à viga.
Além de alguns exemplos já mostrados em figuras anteriores, é possível supor algumas pessoas em pé num apartamento, numa reunião familiar. A força que cada pessoa faz sobre a laje é considerada uma força concentrada.
Observe no croqui da figura, a seguir, a situação descrita para uma dessas pessoas.
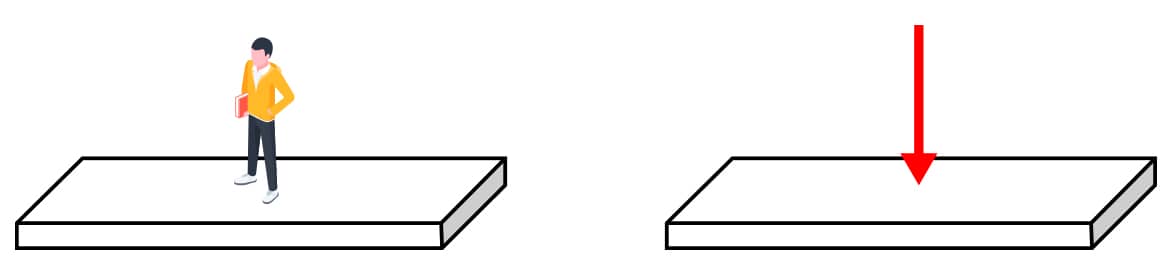
Representação de uma força (carga) concentrada. Fonte: O autor.
Ainda dentro da ideia de carga concentrada, é possível pensar em uma carga momento aplicada sobre uma viga.
Observe o esquema da figura a seguir, em que uma carga momento no sentido horário é aplicada à viga no ponto destacado. Lembrando que o momento é um vetor; em nosso estudo das vigas biapoiadas, perpendicular ao plano da viga, podendo estar “entrando” ou “saindo” deste (regra da mão direita).
No exemplo da figura, o momento é um vetor com direção perpendicular ao plano e “entrando” neste.
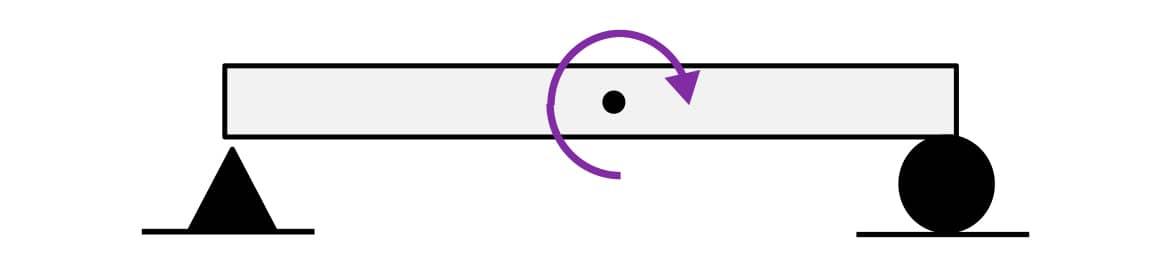
Representação de uma carga momento sobre uma viga.
distribuída
No grupo das cargas distribuídas, é importante ressaltar que elas podem ser apresentadas em termos de distribuição ao longo de uma área, contudo, o estudo deste tema limita-se a vigas biapoiadas e, portanto, a carga será distribuída ao longo de um comprimento.
Suponha uma viga homogênea de comprimento 4m e peso 2.000N. A ideia é distribuir esse peso ao longo do comprimento da viga.
Pelo fato de a viga ser homogênea, há 2.000 N divididos por 4 m equivalendo a q = 500 N/m.
Outro exemplo comum na engenharia civil, a respeito de cargas distribuídas ao longo de um comprimento, é a parede de um apartamento onde os tijolos estão assentados sobre uma base.
A figura seguinte representa a situação real da parede e sua representação gráfica, ou seja, a de uma carga distribuída.
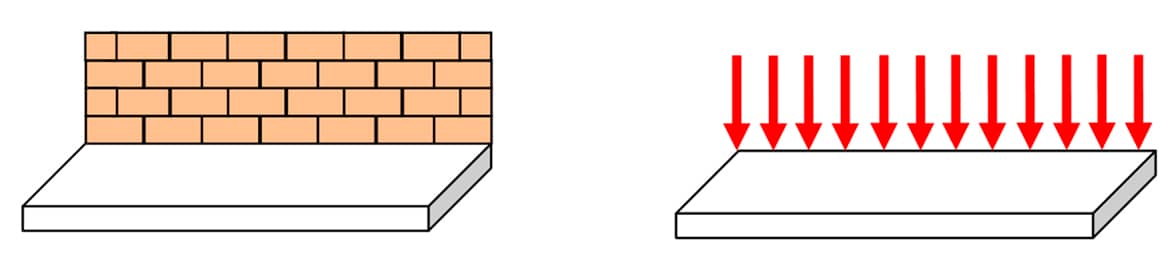
Esquema de força distribuída ao longo de um comprimento. Fonte: O autor.
Substituição de uma carga distribuída por uma concentrada
Em muitas situações, para o cálculo de reações em vigas biapoiadas, será importante fazer a substituição da carga distribuída pela concentrada equivalente.
Essa troca significa conhecer que vetor único (intensidade, direção, sentido e ponto de aplicação) representando uma carga concentrada é capaz de substituir a carga distribuída provocando os mesmos efeitos físicos no sistema.
A figura, a seguir, apresenta uma situação genérica de substituição de uma carga distribuída q(x) pela sua carga equivalente concentrada F.
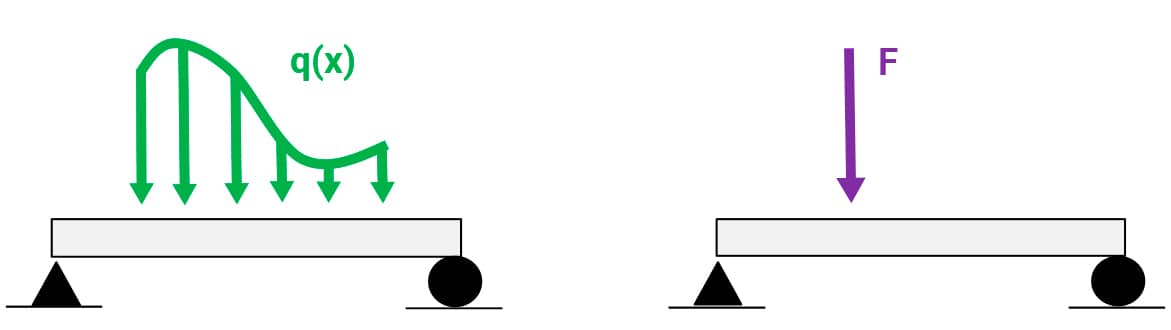
Figura 8 – Substituição de uma carga distribuída por uma concentrada. Fonte: O autor.
Para se determinar a intensidade da força concentrada F, é necessária a determinação da área sob a curva da carga distribuída, ou seja, e do ponto de aplicação (centroide da área sob a curva da carga distribuída).
Dois casos de carregamentos distribuídos são apresentados na figura a seguir (uniformemente e linearmente distribuídos).
A determinação da intensidade e localização (centroide) são bem simples.
Nos dois casos, a intensidade da carga concentrada equivalente será numericamente igual à área do retângulo (base x altura) ou à área do triângulo retângulo (base x altura/2).
• Em relação ao centroide, o do retângulo localiza-se no encontro das diagonais, ou seja, a vertical passa pelo ponto médio da base.
• Quando a carga distribuída for de acordo com um triângulo retângulo, o centroide localiza-se, em relação ao ângulo reto, a 1/3 da base e a 1/3 da altura.
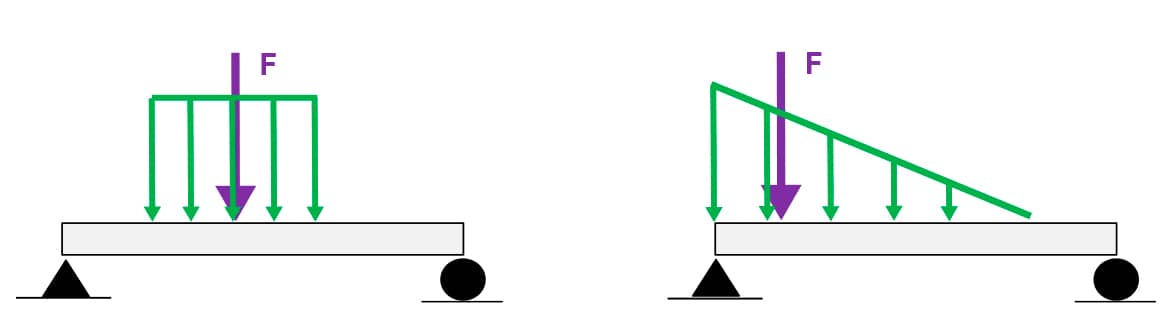
Cargas distribuídas particulares. Fonte: O autor.
Exemplo
Suponha que uma viga biapoiada isostática esteja sob um carregamento distribuído linear, conforme a figura. Considere a viga com comprimento 6 m e peso desprezível. Faça a substituição do carregamento por um equivalente concentrado.
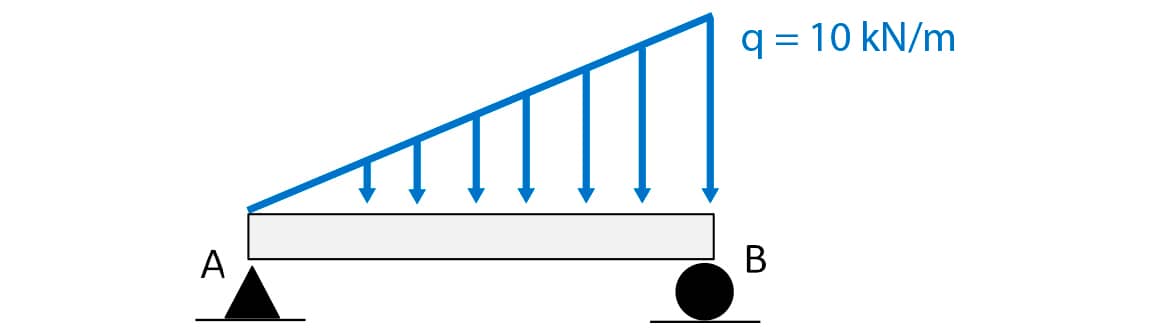
Solução:
Inicialmente, será determinada a intensidade da carga
equivalente ao carregamento
distribuído. O módulo (intensidade) é determinado pela área do triângulo
(b .
h/2 = 10 . 6/2 = 30 kN).
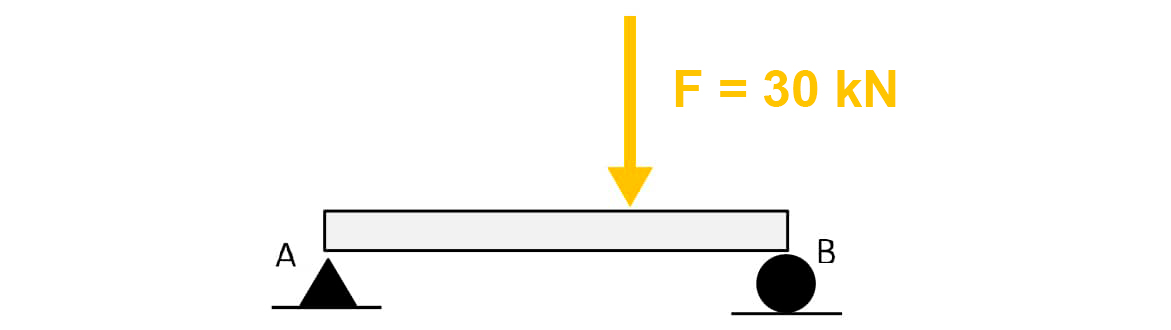
No caso da carga triangular, a linha de ação da carga concentrada equivalente localiza-se a 1/3 do vértice do ângulo reto. Nesse caso, a (1/3) . 6 = 2 m do apoio B.
Assim, a substituição fica de acordo com a figura a seguir.
Mão na Massa
Teoria na prática
Vários ramos da Engenharia apresentam muitos exemplos em que são aplicadas as vigas, um dos principais elementos estruturais para muitos autores.
Na Engenharia Civil, por exemplo, é fácil perceber a presença desses elementos na fase intermediária da construção de um prédio, pois antes do fechamento das paredes, ficam evidentes as vigas, dentre outros elementos estruturais.
Na Engenharia Mecânica também existem exemplos em grandes estruturas metálicas. O modelo prático, que será apresentado, possui algumas simplificações em sua modelagem, mas é didático para a percepção das vigas biapoiadas sob determinado carregamento.
Suponha um carro estacionado (equilíbrio estático) de massa aproximadamente 1.800 kg.
Devido à presença do motor na parte dianteira, o peso não é igualmente distribuído entre os eixos dianteiro e traseiro. Suponha que 40% do peso seja suportado pelo eixo traseiro.
Para simplificar a modelagem, será suposto um eixo contínuo de seção circular constante e comprimento 2,0 m. Além disso, será feito um estudo que envolve o modelo físico, sua representação esquemática por meio do diagrama do corpo livre (DCL) e cálculos das reações nos apoios.
Inicialmente, será determinado o peso do carro e a fração desse suportada pelo eixo traseiro.
Considerando a aceleração da gravidade local igual a 10m/s2, o peso (P = m.g) será igual a 1800.10, ou seja, 18.000 N (18 kN). Apenas 40% desse valor é suportado pelas rodas traseiras. Dessa forma, 40% x 18 kN é igual a 7,2 kN.
A seguir, há um esquema do eixo e as rodas traseiras vistos sob a óptica de um observador localizado na parte posterior do carro.

O eixo é uma viga biapoiada em que as rodas são os vínculos.
Considerando que o valor de 7,2 kN seja distribuído uniformemente ao longo do comprimento do eixo, é possível imaginar um modelo de uma carga distribuída sobre ele.
Dessa forma, a carga distribuída q será dada por 7,2 kN divididos por 2 m, ou seja:
q = 7,2 / 2 = 3,6 kN/m.
Na figura, a seguir, veja o DCL para a situação descrita.
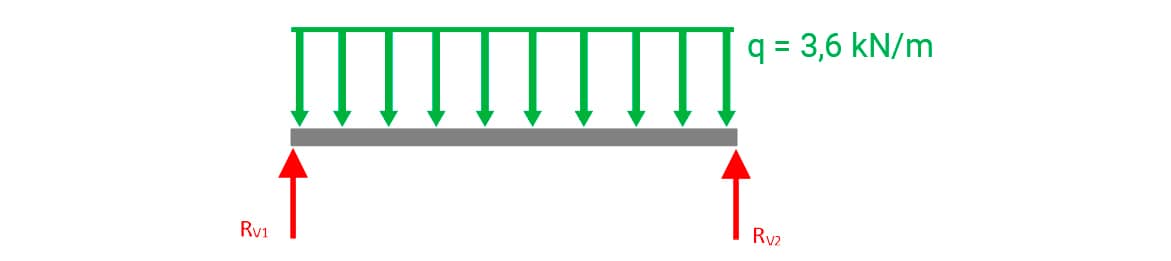
A partir das equações do equilíbrio estático (equilíbrio translacional) e (equilíbrio rotacional) é possível determinar os valores de RV1 e RV2.
No caso apresentado, pela simetria da configuração geométrica e do carregamento, é imediata a determinação das reações, uma vez que elas serão iguais.
A carga distribuída equivale a uma força concentrada de intensidade igual à área do retângulo, b . h = 3,6 . 2 = 7,2 kN que atua no ponto médio do eixo.
Na equação do equilíbrio em y, tem-se:
Como as reações (RV1 e RV2) são iguais, RV1 + RV1 = 7,2 → 2.RV1 = 7,2 → RV1 = 7,2/2 = 3,6 kN.
Assista agora à análise de um caso real
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Calcular os efeitos internos de flexão e cisalhamento numa viga biapoiada isostática
Introdução
Considere uma viga sob um carregamento externo genérico.
Ao se estudar internamente as seções desse elemento estrutural, é possível perceber os efeitos decorrentes das ações externas. Cada seção interna pode estar submetida aos seguintes efeitos: flexão, torção e os esforços cortante e normal.
A abordagem desse tema particulariza a viga e o carregamento aplicado. A suposição é que a viga se encontra biapoiada com um carregamento (força) no seu plano e momentos fletores perpendiculares a esse plano. Serão avaliados apenas os efeitos interno de cisalhamento (esforço cortante) e de flexão (momento fletor).
A figura a seguir mostra essa situação de maneira esquemática.
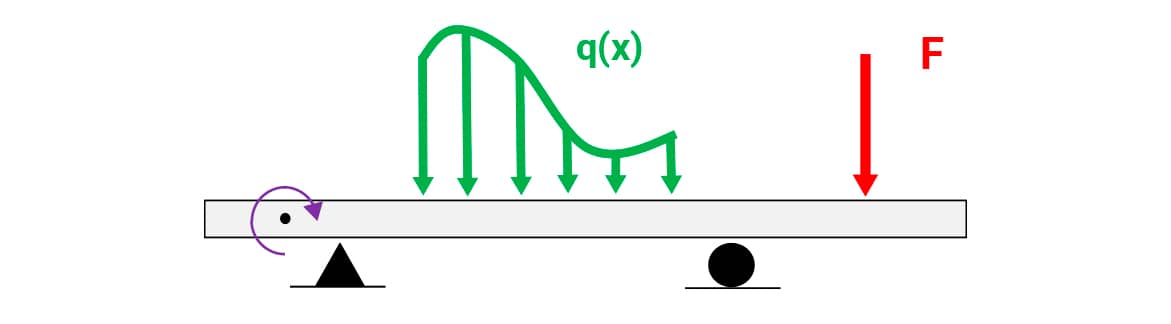
Viga biapoiada sob carregamento no plano.
Efeitos internos de flexão e de cisalhamento
Ao se estudar os efeitos internos numa seção de uma viga sob um carregamento, é fundamental que o aluno perceba que o corte feito para “expor” a seção interna de estudo é tão somente uma abstração. Não ocorre, de fato, um rompimento físico da viga.
Ao se efetuar o corte (a_a’) na viga, duas “partes” dessa surgirão (à esquerda e à direita do plano de corte).
Será possível, portanto, o estudo da seção interna a partir de uma dessas duas partes em que a viga se dividiu (abstratamente).
Observe o corte da viga na figura:
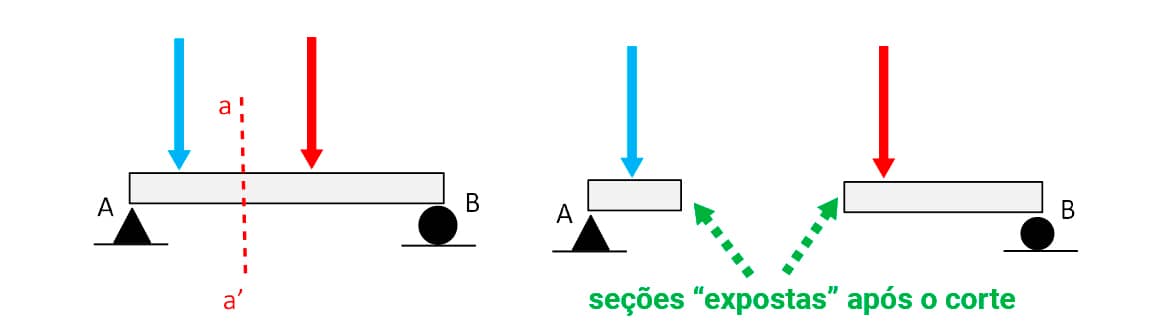
Corte de uma viga e as seções “expostas”.
Com o corte da viga e a exposição da seção interna, os efeitos internos são indicados por M (momento fletor) e V (esforço cortante). A figura, a seguir, apresenta estes dois vetores (M e V) na seção interna em ambas as partes da viga.
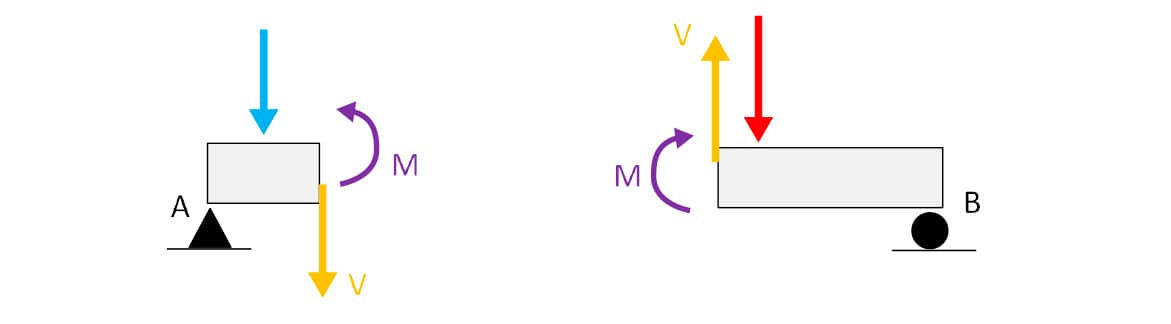
Esforços internos – momento fletor e esforço cortante.
A figura anterior mostra o esforço cortante V (tangente à seção interna) e o momento fletor M convencionados como positivos. Perceba a Terceira Lei de Newton (ação-reação) sendo aplicada.
O momento fletor na parte esquerda da viga tem sua reação na parte da direita, assim como o esforço cortante.
Atenção
Atente que os pares de M e V têm sentidos opostos, como prevê a Terceira Lei de Newton.
Determinação dos efeitos internos de flexão e cisalhamento em uma viga
Para a determinação dos efeitos internos (esforço cortante V e momento fletor M), em uma dada seção da viga, serão utilizadas as equações do equilíbrio estático do corpo rígido bidimensional, ou seja:
- (equilíbrio translacional)
- (equilíbrio rotacional)
Em linhas gerais, inicialmente são determinadas as reações nos apoios da viga, considerando-a como um corpo único. Conhecendo-se os valores das reações nos vínculos da viga, faz-se o corte na região da viga que se deseja estudar e separa-se uma das duas partes.
Uma vez que a viga se encontra em equilíbrio, qualquer uma das partes escolhidas também estará em equilíbrio. Assim, novamente as equações do equilíbrio são utilizadas e os valores de V e M são determinados.
O exemplo a seguir mostra os passos descritos.
Exemplo
(FCC ‒ 2014 ‒ TRF - 3ª REGIÃO ‒ Analista Judiciário ‒ Engenharia Civil). Considere a figura:
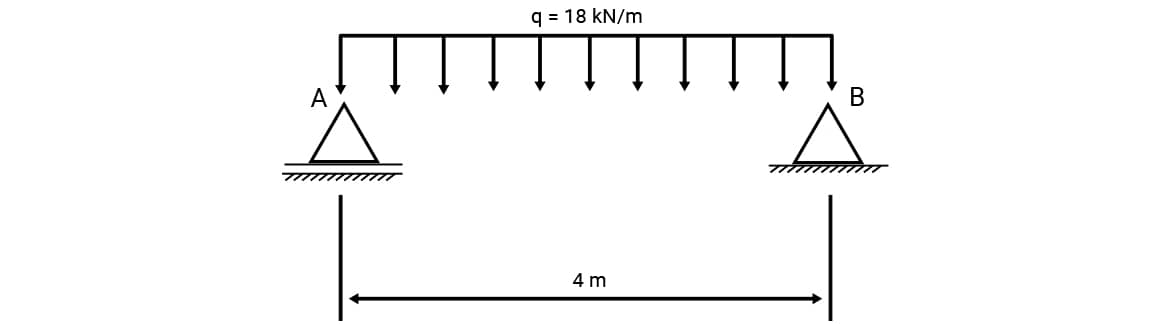
O momento fletor, distante 1m do apoio A, em kN.m, será igual a:
A) 36
B) 18
C) 27
D) 72
E)
9
Solução:
1º passo: Determinação das reações nos apoios
Inicialmente, será feita a “troca” da carga distribuída pela carga concentrada equivalente e desenhado o DCL da barra.
A intensidade da carga concentrada é dada pela área do
retângulo, ou seja,
b . h = 18 . 4 = 72 kN e seu ponto de aplicação no ponto
médio da viga (4/2 = 2 m).
Os apoios A e B são, respectivamente, do primeiro e segundo gêneros. Em A existe uma reação vertical (VA) e em B duas reações, uma vertical (VB) e outra horizontal (HB).
Segue o diagrama do corpo livre da viga.
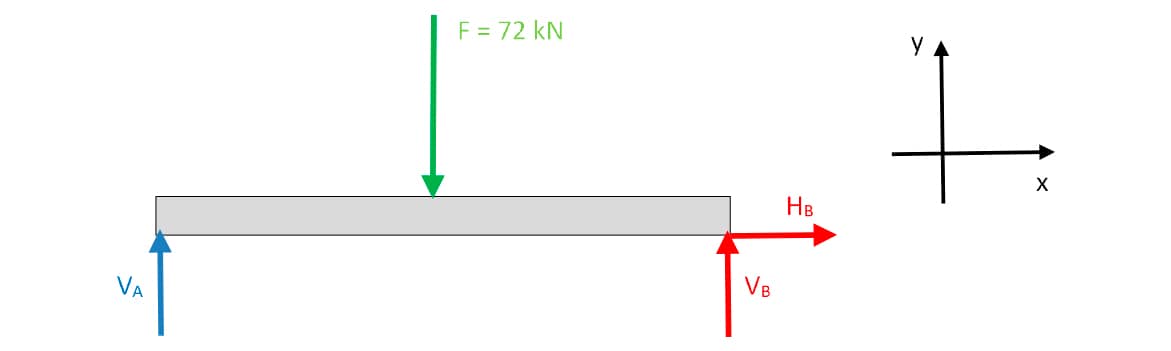
Aplicando-se as equações de equilíbrio do corpo rígido:
- (sentido anti-horário do momento positivo). Aplicando-se o momento das forças em relação ao ponto B, tem-se 72 . 2 – VA . 4 = 0. Logo, 144 - 4.VA = 0, ou ainda 4.VA = 144 → VA = 144/4 = 36 kN. Da equação (*), VA + VB = 72.
Substituindo VA = 36 kN, tem-se 36 + VB = 72 → VB = 72 – 36 = 36 kN.
Comentário
Nesse exemplo, em particular, o carregamento e a simetria do problema facilitam a determinação das reações. Como não há carregamento horizontal, HB = 0 e, pela simetria do carregamento, VA = VB = 36 kN.
2º passo:
Determinação dos esforços internos na seção de estudo
Observe na figura do exemplo o plano de seccionamento distante 1 m do apoio A.
Fazendo o corte na viga e escolhendo-se a parte esquerda, tem-se:
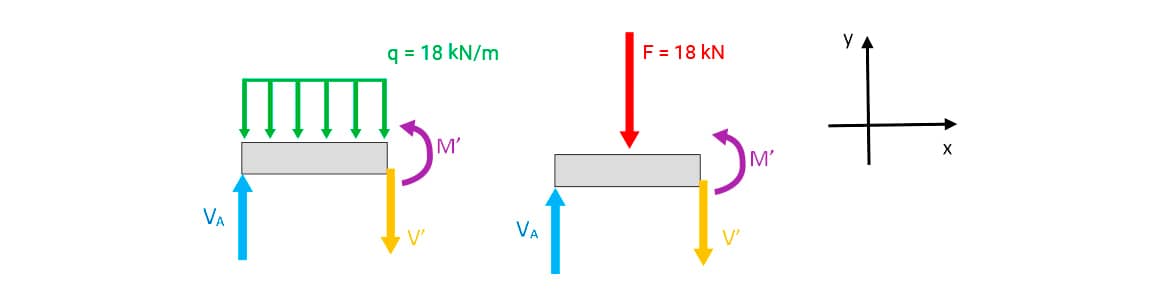
Perceba que na parte esquerda da viga, o carregamento distribuído atua apenas sobre o comprimento de um metro (corte).
Na figura à direita, há o DCL com a representação da força concentrada equivalente (área do retângulo b . h = 18 . 1) de 18 kN atuando a 0,5 m de A.
Aplicando-se as equações de equilíbrio do corpo rígido:
• (satisfeita)
•
• (sentido anti-horário do momento positivo).
Aplicando-se o momento das forças em relação ao ponto C (seção do corte), tem-se:
• M’ + F' . 0,5 – VA . 1 = 0.
• Logo, M’ + 18 . 0,5 – 36 . 1 = 0.
• Assim, M’ + 9 – 36 = 0 → M’ = 36 – 9 = 27 kN.m
Mão na Massa
Teoria na prática
Um projeto tem várias etapas que culminam na concepção do produto. Neste momento do tema, iniciamos o estudo para o dimensionamento de um elemento estrutural muito presente em vários ramos da Engenharia: a viga.
Em passos futuros, outros conceitos serão apresentados, mas que necessariamente carecerão dos conceitos aprendidos na disciplina.
Suponha que um aluno esteja estagiando e auxiliando em um projeto cujo engenheiro responsável pediu que o estagiário determinasse os esforços internos (cortante e momento fletor) em uma viga a 1 m da sua extremidade esquerda.
O aluno lembrou de suas aulas de Mecânica dos Sólidos e, percebendo que precisava de mais informações, falou com o engenheiro, que disse que a viga em questão tem comprimento 3 m e um carregamento linear crescente, a partir da extremidade esquerda (0) até a extremidade direita (12 kN/m). Ainda pensando sobre a questão, o aluno perguntou ao engenheiro como essa viga estava vinculada.
A resposta foi que era biapoiada, sendo os apoios de segundo e primeiro gêneros, à esquerda e à direita da viga, respectivamente.
Com todas essas informações, o aluno criou o modelo mostrado na figura a seguir.
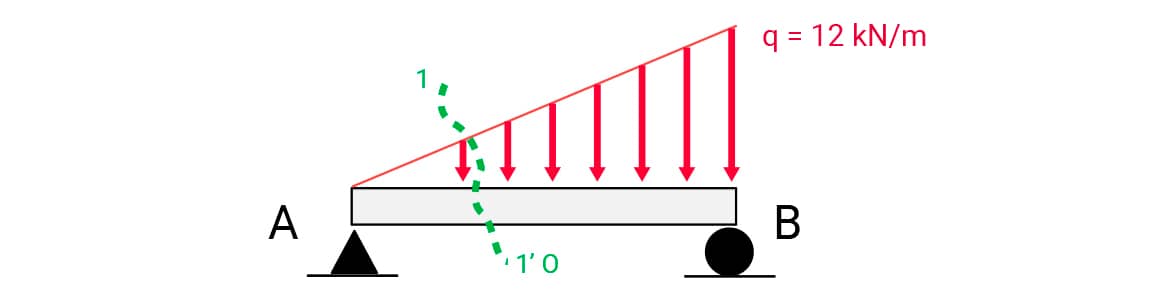
Inicialmente, o aluno determinou as reações nos apoios A e B. O primeiro passo foi fazer a substituição do carregamento distribuído linearmente pela carga concentrada equivalente.
A intensidade da carga concentrada equivale à área do triângulo, ou seja,
F
= (b . h)/2 = (12 . 3)/2 = 18 kN.
O ponto de aplicação fica a 1/3 do ângulo reto, no caso descrito, o apoio B. Assim, F terá ponto de aplicação a 1 m de B.
Na figura, seguinte, está o DCL da viga determinado pelo aluno.
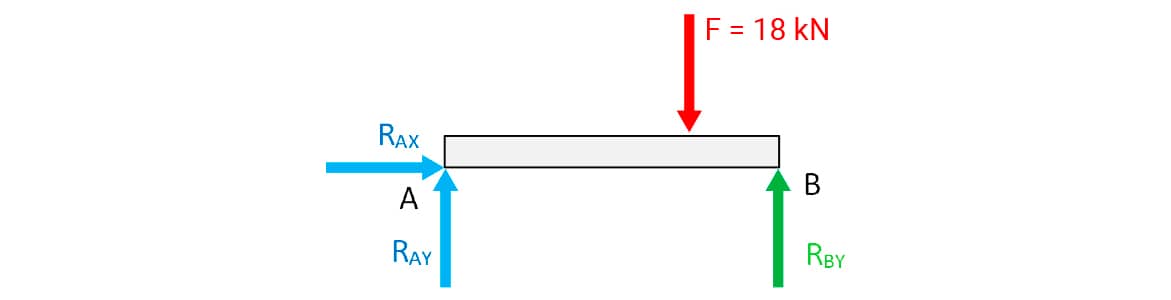
O aluno aplicou as equações de equilíbrio do corpo rígido:
•
•
• (sentido anti-horário do momento positivo).
Momento das forças em relação a A, tem-se .
Da equação
Determinadas as reações, o aluno fez o corte (1_1’) mostrado na figura de seu modelo inicial e desenhou o DCL da parte esquerda da viga. O modelo para esse corte é mostrado na figura a seguir.
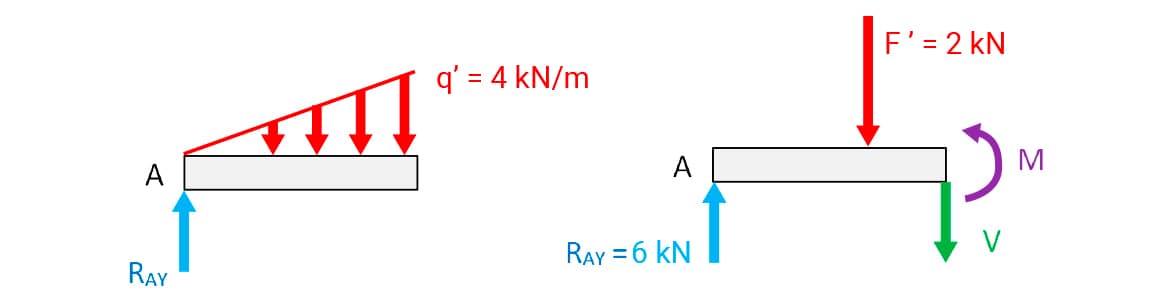
O valor da carga concentrada equivalente foi determinado pelo aluno calculando a área do triângulo (4.1)/2 = 2 kN. O ponto de aplicação encontra-se a 1/3 m da seção de corte. O valor de q’ é proporcional à distância ao ponto A. Para 3 m, o valor é de 12 kN/m, para 1 m (3 vezes menor), q’ será dado por 12/3 = 4 kN/m.
Novamente, o aluno aplicou as equações de equilíbrio do corpo rígido:
• (satisfeita)
•
• (sentido anti-horário do momento positivo). Momento das forças em
relação à seção de corte, tem-se
2 . (1/3) – 6 . 1 + M = 0 → 2/3 – 6 + M = 0 → M
= 6 – 2/3 → M = 16/3 kN.m.
Caso real de determinação dos esforços internos em uma viga.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Esquematizar os diagramas de estado de vigas biapoiadas isostáticas
Introdução
A apresentação deste tema baseia-se apenas no estudo e compreensão dos esforços internos cortante e de flexão em uma viga.
• No módulo anterior, fizemos exemplos e exercícios para mostrar a metodologia de como determinar esses esforços para uma seção particular da viga.
• Neste momento, apresentaremos uma análise geral.
Considerando o eixo da viga como o eixo x, por exemplo, e as extremidades com valores zero e L (comprimento da viga), será possível determinar expressões para o esforço cortante e o momento fletor como função de x, ou seja, V(x) e M(x).
A partir das expressões V(x) e M(x), vários aspectos podem ser abordados. É possível plotar os gráficos do diagrama de esforço cortante (DEC) e do diagrama do momento fletor (DMF). Ademais, é possível a determinação do valor do esforço cortante/ momento fletor em quaisquer pontos da viga diretamente a partir das expressões V(x) e M(x).
Comentário
Outro aspecto é a determinação de valores específicos e a posição em que eles ocorrem, como o momento fletor máximo em uma viga sob dado carregamento e a sua localização na viga.
Complementando o estudo do DEC e do DMF, serão apresentadas equações diferenciais que relacionam o carregamento q(x), V(x) e M(x) e algumas propriedades geométricas dos diagramas que auxiliam na elaboração deles.
Elaboração dos diagramas de esforço cortante (DEC) e momento fletor (DMF) de vigas biapoiada
Antes de efetivamente determinarmos o DEC e o DMF de uma viga, será adotada a convenção de que os valores positivos de V e M estarão acima do eixo longitudinal da viga e os valores negativos, abaixo.
Na figura, a seguir, há um exemplo de uma viga biapoiada com carregamento uniformemente distribuído e o DEC e o DMF correspondentes com a convenção de sinais adotada.
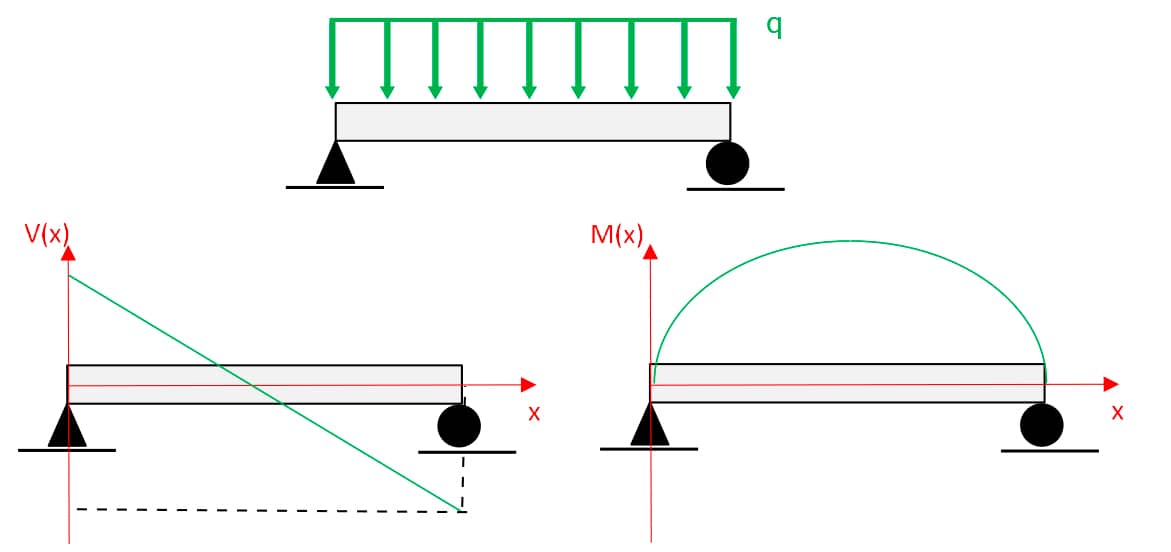
DEC e DMF de uma viga biapoiada.
Em linhas gerais, a determinação das expressões V(x) e M(x) é feita iniciando-se pelo cálculo das reações de apoios da viga.
Após, é feito um corte genérico a uma distância x da origem (extremidade esquerda da viga) e estuda-se a parte esquerda da viga em termos de equilíbrio, ou seja, são aplicadas as equações:
(equilíbrio translacional) e (equilíbrio rotacional).
Dessa forma, serão determinadas expressões para o esforço cortante e para o momento fletor em função da variável x. Generalizando, por vezes são necessários cortes distintos em função do carregamento.
A fim de que essas ideias qualitativas da metodologia sejam entendidas de forma quantitativa, segue um exemplo para a construção do DEC e do DMF de uma viga biapoiada.
Exemplo:
Suponha uma viga biapoiada de comprimento L e com uma carga concentrada F distante a unidades de comprimento do apoio A e b unidades de comprimento do apoio B. Dessa forma, a + b = L.
Observe a figura a seguir.
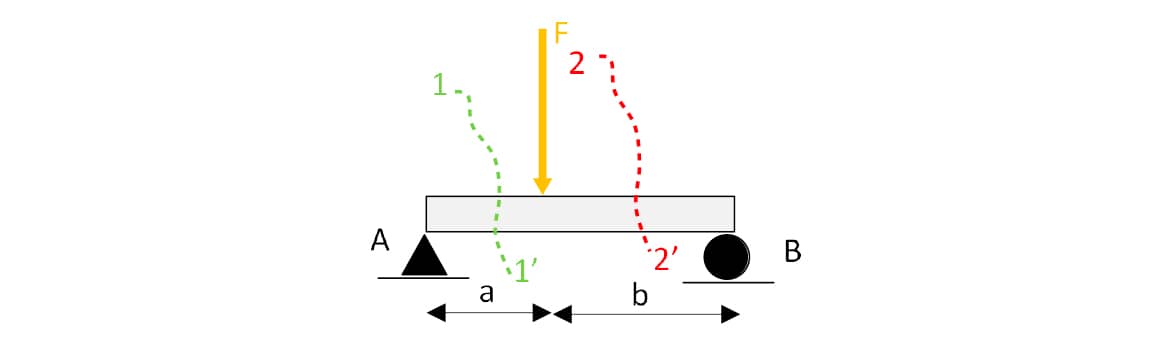
Determinação das reações nos apoios. Observe o diagrama do corpo livre da barra.
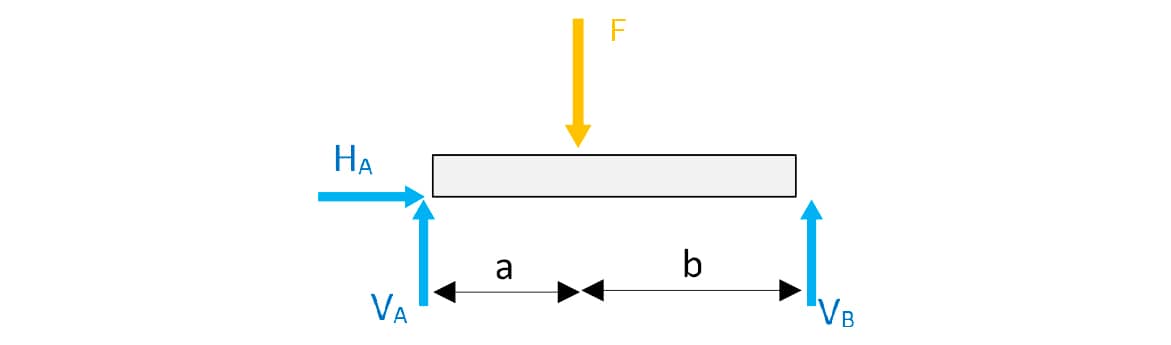
Aplicando-se as equações de equilíbrio do corpo rígido à viga, tem-se:
- (satisfeita)
- (sentido anti-horário do momento positivo).
Aplicando-se o momento das forças em relação ao ponto de apoio A, tem-se:
- - F . a + VB . (a + b) = 0. A soma dos valores de a e b vale o comprimento da barra (a + b = L).
- Substituindo na equação
- Substituindo VB em (*), tem-se:
Dois cortes serão feitos (mostrados na figura inicial do exemplo).
O primeiro corte (1_1’) levará a uma expressão válida no intervalo 0 até a, ou seja, à esquerda do ponto de aplicação de F.
O outro corte levará a uma expressão que valerá no intervalo de a até L, ou seja, à direita do ponto de aplicação de F. Observe o DCL na figura após o primeiro corte da viga.
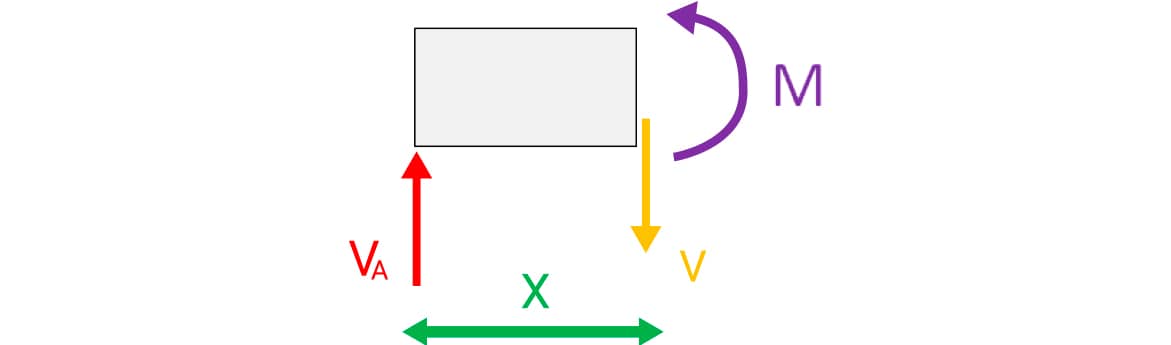
Aplicando-se as equações de equilíbrio translacional e rotacional do corpo rígido:
- (sentido anti-horário do momento positivo). Aplicando-se o momento das forças em relação ao ponto da seção do corte, tem-se M – VA.x = 0.
- Substituindo
Observe a figura, após o segundo corte (2_2’) da viga, após o ponto de aplicação da força concentrada F.
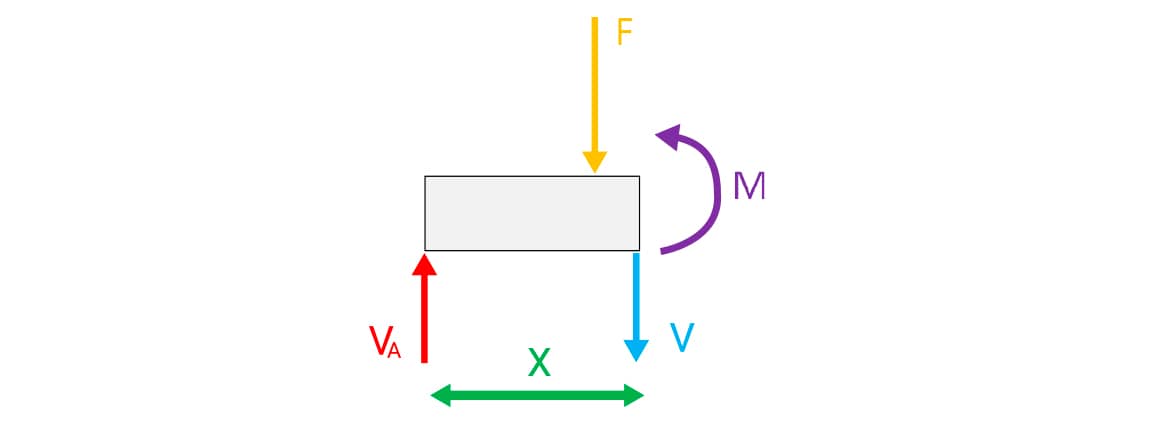
Aplicando-se as equações de equilíbrio translacional e rotacional do corpo rígido:
- (sentido anti-horário do momento positivo).
Aplicando-se o momento das forças em relação ao ponto da seção do corte, tem-se:
- M + F.(x-a) – VA.x = 0.
- Substituindo VA tem-se,
A partir de agora, com as expressões encontradas para V e M, serão traçados os gráficos que representam o esforço cortante e o momento fletor nas seções da viga ao longo de seu comprimento.
Diagrama do esforço cortante (DEC):
- Parte à esquerda do ponto de aplicação da força F tem V(x) dada pela função constante . Assim, uma reta paralela ao eixo x, acima do zero.
- Parte à direita do ponto de aplicação da força F tem V(x) dada pela função constante . Assim, uma reta paralela ao eixo x, abaixo do zero.
Dessa forma, a seguir, há o esboço do DEC.
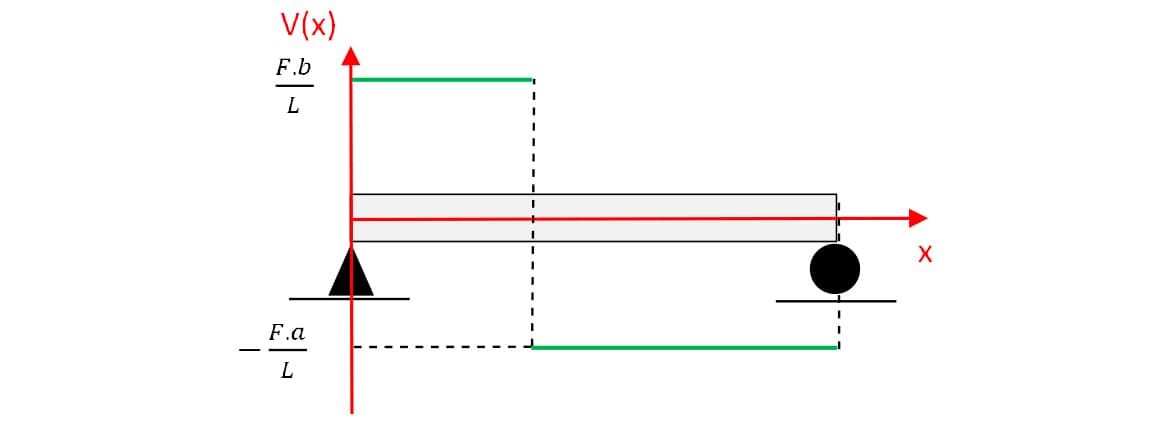
Atenção
Note que no DEC há uma descontinuidade no gráfico no ponto de aplicação da força concentrada F. Perceba que esse “degrau” tem valor igual a F.
Diagrama do momento fletor (DMF):
- Parte à esquerda do ponto de aplicação da força F tem M(x) dada pela função do 10 grau . Então, uma reta crescente de x = 0 (M =0) até .
- Parte à direita do ponto de aplicação da força F tem M(x) dada pela função do 10 grau . Assim, uma reta decrescente de até x = L (M = 0).
Dessa forma, a seguir, há o esboço do DMF.
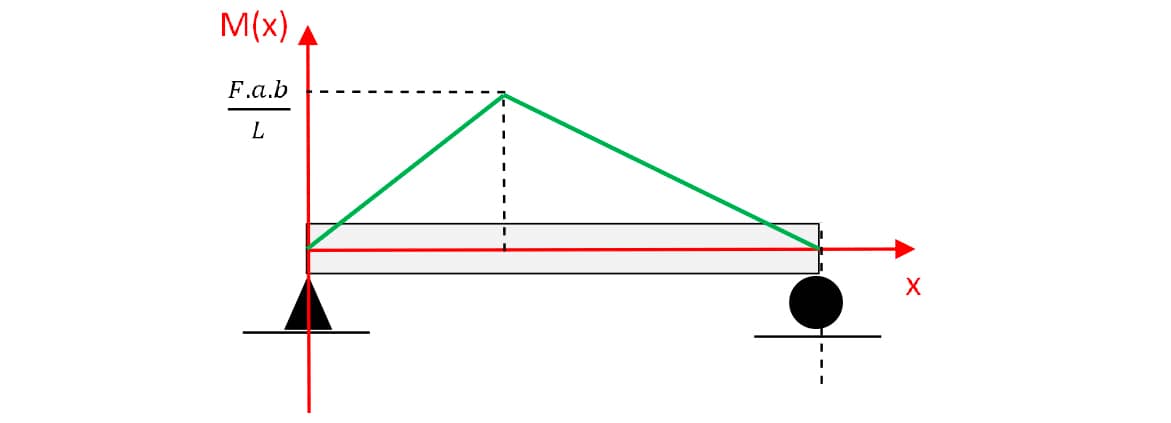
Atenção
Note que o momento fletor máximo ocorre no ponto de aplicação da força F (descontinuidade do DEC) e seu valor é dado por .
Relações matemáticas entre carregamento, esforço cortante e momento fletor e propriedades geométricas do DEC e DMF
O procedimento descrito, anteriormente, é uma forma de encontrar as expressões do esforço cortante e do momento fletor em função da posição x da seção interna da viga.
Contudo, para carregamento q(x) com expressões complexas não é o método mais adequado.
Por isso, é importante estudar uma metodologia que auxilie nessa situação. É possível demonstrar que as seguintes relações são válidas entre q(x), V(x) e M(x).
• (Equação 1)
• (Equação 2)
• (Equação 3)
A partir da equação 1, é possível concluir que, em cada ponto ao longo do comprimento da viga, o coeficiente angular da tangente ao DEC equivale a – q(x) aplicada no ponto.
Cuidados devem ser tomados para aplicação da equação 1 para cargas concentradas, pois levam a descontinuidades no DEC.
A partir da equação 2, integrando-a, tem-se
Assim, a variação do momento fletor em um dado trecho corresponde à área do DEC nesse trecho da viga.
Para funções polinomiais, é verdade que se q(x) é de grau “n”, V(x) será de grau “n + 1” e M(x) de grau “’n + 2”.
A partir das expressões anteriores, será utilizado um exemplo para mostrar a aplicação na montagem dos DEC e DMF.
Exemplo:
Barra biapoiada de comprimento L com carregamento uniformemente distribuído.
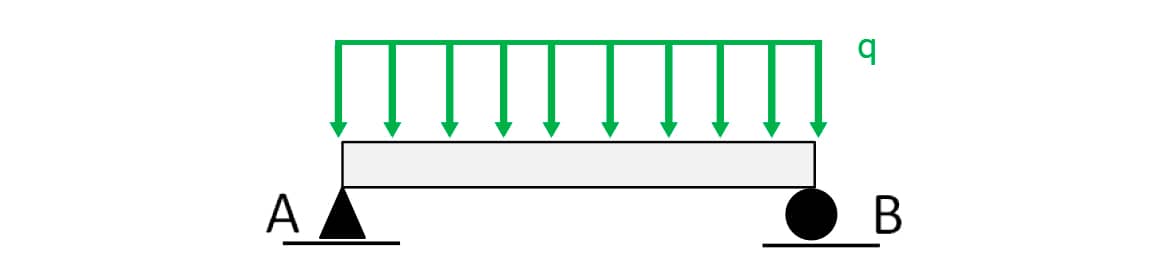
A carga concentrada equivalente é igual à área do retângulo, ou seja, q.L. Pela simetria, as reações em A e B serão iguais a qL/2.
O carregamento é uma função constante (polinômio de grau 0), logo V(x) será um polinômio de grau 1 e M(x) um polinômio de grau 2.
O carregamento é dado por q(x) = q (constante).
Note que em x = 0, ponto A, o esforço cortante é igual a V(0) = VA = q.L/2.
Assim, substituindo na última equação, tem-se:
Observe que é uma função do primeiro grau (reta) com coeficiente angular negativo (decrescente).
Assim, substituindo na última equação, tem-se:
Para e para .
Logo, o DEC terá o seguinte aspecto:
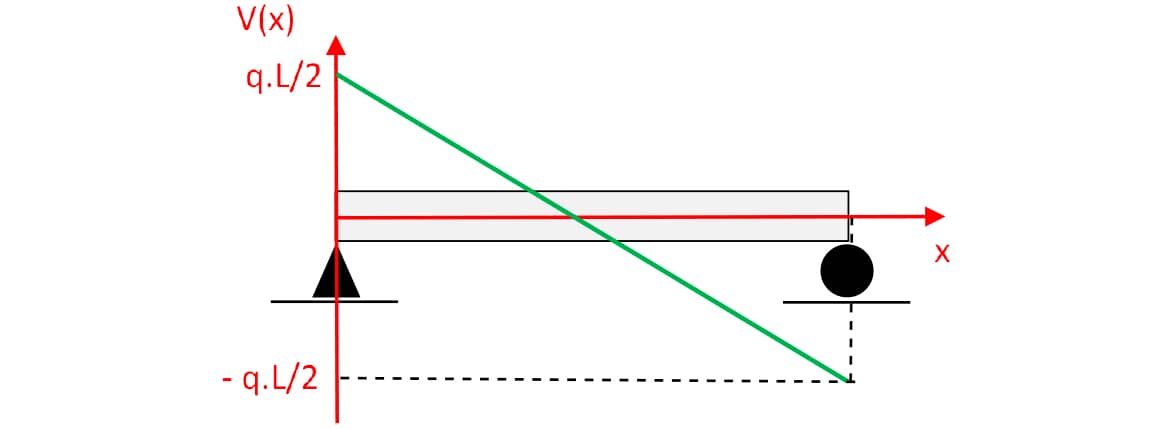
A partir da função encontrada é possível determinar em que ponto o esforço cortante é nulo, pois .
Logo, em x = L/2, o esforço cortante é nulo.
Para a confecção do DMF, será utilizada a equação 2.
Integrando, tem-se:
Como os apoios da viga são de primeiro e segundo gêneros, não restringem a rotação, logo M(0) = M(L) = 0.
Substituindo na expressão anterior, tem-se
Dessa forma, a expressão para o momento fletor M(x) será
O aspecto do DMF é mostrado na figura a seguir.
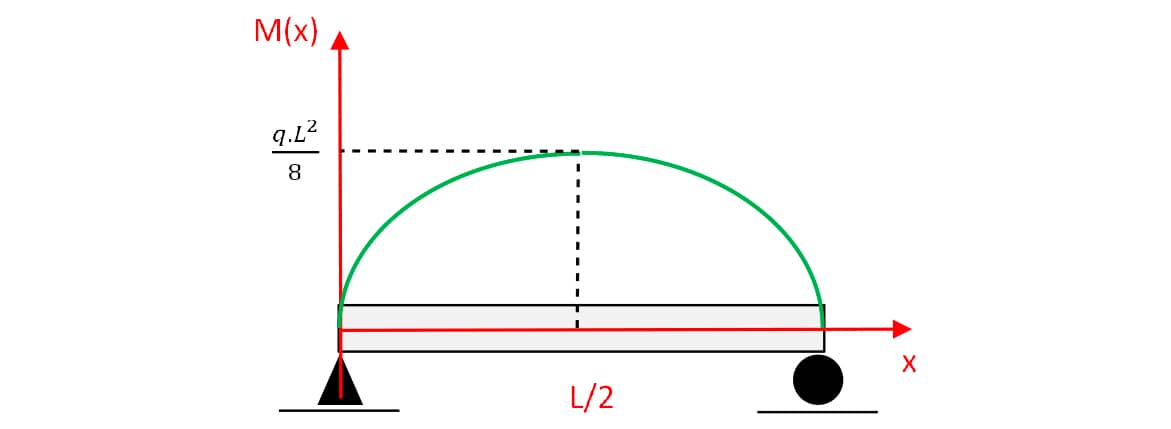
Note que o valor máximo do momento fletor é e ocorre em x = L/2.
É fácil mostrar esses valores, pois basta derivar a função de M(x) em relação a x e igualar a zero, ou seja,
Substituindo x = L/2 em
Outra maneira de desenhar o DMF é a partir da ideia que foi citada, anteriormente, de que a área sob o DEC corresponde ao acréscimo/decréscimo do momento fletor.
Atenção
Partindo do conceito de que os dois apoios não restringem rotação, os valores inicial e final do momento fletor são nulos. Como o DEC é uma reta (grau 1), o DMF será uma parábola (grau 2).
No DEC, o primeiro triângulo tem área igual a .
Dessa forma, somando-se esse valor ao zero, chega-se ao
valor do momento fletor em
x = L/2.
O segundo triângulo no DEC tem área “negativa” igual a .
Adicionando-se esse valor a , encontra-se zero, ou seja,
o valor do momento fletor em x = L.
Mão na Massa
Teoria na prática
No módulo anterior, o Teoria na prática apresentou um aluno estagiário de uma empresa auxiliando um engenheiro na determinação do cálculo dos esforços internos cortante e fletor, numa dada seção da viga.
O estagiário conseguiu resolver o que lhe fora pedido e recebeu uma nova incumbência: determinar os mesmos esforços internos em outra seção da mesma viga.
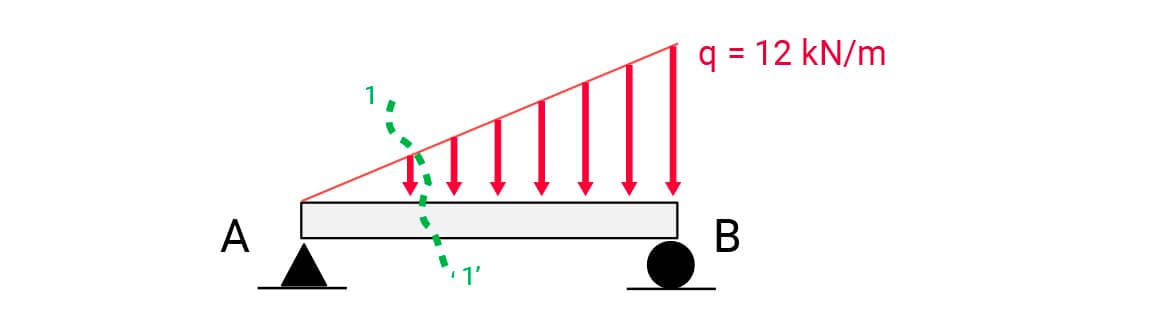
O aluno concluiu que uma adaptação na solução encontrada no primeiro caso levaria à solução desejada. Porém, ele optou por determinar o esforço cortante e o momento fletor em uma região genérica qualquer da viga.
Dessa forma, ao determinar as expressões para V(x) e M(x), poderia ter os valores em quaisquer seções e ainda ratificar o resultado encontrado inicialmente.
Como a viga a ser estudada era a mesma, o modelo criado inicialmente não mudou, como apresenta a figura.
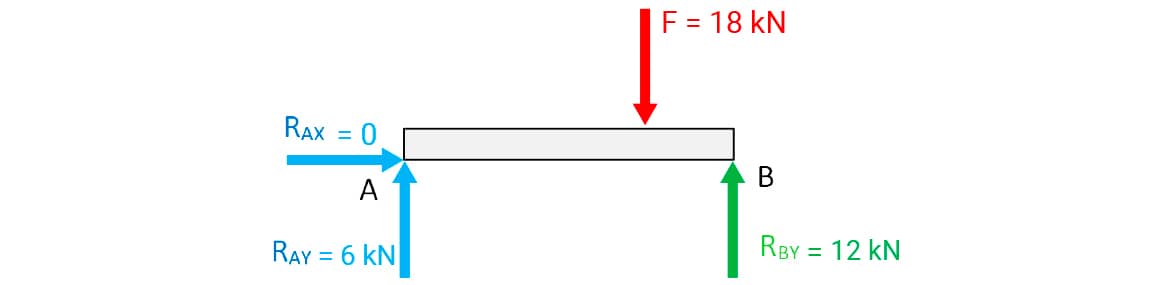
Os valores encontrados para as reações em A e B também poderiam ser reutilizados.
Na figura seguinte está o DCL da viga com os valores previamente determinados pelo aluno.
Determinadas as reações, o aluno fez o corte genérico (1_1’) mostrado na figura de seu modelo inicial, localizado a x m do apoio A, e desenhou o DCL da parte esquerda da viga. O modelo para esse corte é apresentado a seguir.
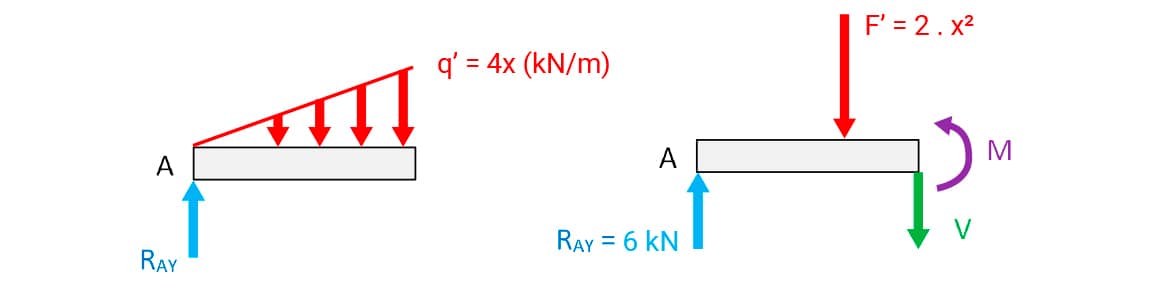
O valor da carga concentrada equivalente foi determinado pelo aluno calculando a área do triângulo (4x .x /2 = 2.x2). O ponto de aplicação encontra-se a x/3 m da seção de corte.
O valor de q’ é proporcional à distância ao ponto A. Assim, q’ = 4.x.
Novamente, o aluno aplicou as equações de equilíbrio do corpo rígido:
- (satisfeita)
- (x em m e V em kN)
- (sentido anti-horário do momento positivo). Momento das forças em relação à seção de corte, tem-se 2.x2 (x/3) – 6 . x + M = 0. Logo, (x em metros e M em kN.m).
Aproveitando as expressões de V(x) e M(x), o aluno fez um teste para os valores pedidos pelo engenheiro no caso descrito no módulo 2, ou seja, para x = 1 m. Substituindo esse valor em V(x) e M(x), encontrou:
- (confirmado)
- (confirmado)
Assista ao vídeo Determinação de expressões para o cálculo dos esforços internos em uma viga – caso concreto.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 4
Compreender a modelagem computacional das vigas biapoiadas isostáticas
Introdução
De forma similar ao estudo feito para as treliças simples isostáticas, neste módulo faremos uma abordagem inicial da modelagem computacional das vigas biapoiadas isostáticas.
Existem muitas ferramentas computacionais acadêmicas/profissionais que auxiliam na determinação de, por exemplo, esforços internos de uma viga.
Contudo, muitos aspectos são considerados nos modelos e que ainda não foram abordados nessa fase do curso de Engenharia. Portanto, a abordagem apresentará um viés qualitativo, mas com possibilidade de alcançar resultados para modelos ainda bem simplificados.
Na Engenharia, as situações reais devem ser entendidas fisicamente para que sejam modeladas matematicamente e, por fim, determinar a solução (de maneira analítica ou computacional). Essas fases são, de maneira genérica, executadas pelos seguintes passos:
1º passo:
Compreensão de todos os aspectos físicos teóricos associados à situação real para a elaboração de um modelo físico que reproduza com a maior realidade a situação a ser estudada.
2º passo:
Tendo um modelo físico que reproduza a situação real e dependendo das condições impostas para o projeto, algumas simplificações podem ser introduzidas no modelo inicial, porém de maneira criteriosa para não comprometerem os resultados. Essas simplificações no modelo propiciam uma diminuição do grau de complexidade matemática do passo seguinte.
3º passo:
A partir das simplificações adotadas no modelo físico inicial, decorre a modelagem matemática, isto é, equacionar matematicamente os fenômenos físicos.
4º passo:
Uma vez que já estão definidas as equações matemáticas e as condições conhecidas (condições iniciais, condições de contorno etc.) é o momento de resolver o problema. A escolha de uma solução analítica é possível. Porém, por vezes, demandará tempo excessivo ou, até mesmo, a impossibilidade da solução. Nesses casos, a escolha de uma ferramenta computacional adequada já existente é conveniente. Por vezes, uma solução computacional própria também pode ser utilizada, por exemplo, para situações novas que ainda não foram amplamente estudadas a ponto de se desenvolver um software.
Análise física de uma viga e sua modelagem matemática
Em nosso estudo, a modelagem física de uma viga já será precedida de algumas simplificações:
- A viga é isostática, ou seja, o número de equações do equilíbrio do corpo rígido é igual ao número de incógnitas (reações nos apoios).
- A viga encontra-se biapoiada.
- A viga é rígida, ou seja, indeformável.
- O carregamento ocorre no plano da viga.
- A princípio, os pesos das vigas são desprezíveis quando comparados às forças externas.
Atenção
Na eventualidade de se considerar os pesos das vigas, adotar-se-á que essa é homogênea e, portanto, o seu peso é uniformemente distribuído ao longo de seu comprimento.
Em linhas gerais, para a determinação das reações nos apoios, serão feitas substituições de cargas distribuídas q(x) por cargas concentradas equivalentes F (intensidade e ponto de aplicação) e o diagrama do corpo livre da viga.
Para determinar a intensidade de F é necessária a determinação da área sob a curva de carregamento, ou seja, encontrar a integral definida dada por e, para determinar o ponto de aplicação é necessário conhecer o centroide da área sob a curva da carga distribuída.
O ponto de aplicação tem linha de ação passando por esse centroide, atuando na viga. O centroide é determinado pela integral .
O DCL é esquematizado a partir dos cálculos anteriores, as eventuais cargas concentradas e as reações nos apoios (que dependem do gênero do apoio).
Primeira fase
Já nessa primeira fase da resolução, é possível perceber uma eventual dificuldade matemática: a resolução das integrais. A resolução por métodos numéricos (ferramenta computacional) é uma opção. Dependendo da necessidade de maior ou menor precisão, adota-se um método numérico ou outro.
Segunda fase
Na segunda fase, surgem as 3 equações do equilíbrio. Como no caso das treliças, um sistema de equações lineares deve ser resolvido. A utilização de um método numérico também pode ser útil, como, por exemplo, o método de Gauss Jordan. Mais uma vez o auxílio de ferramentas computacionais já desenvolvidas pode diminuir o tempo de resolução.
Feita essa fase inicial de determinação das reações, um modelo será apresentado para que uma função possa descrever os esforços internos com dependência da posição x da seção. Tendo essas funções, é possível utilizar uma ferramenta computacional para desenhar os diagramas de esforço cortante e momento fletor (DEC e DMF).
A Pontifícia Universidade Católica do Rio de Janeiro (PUC-RJ), por meio de um de seus professores, Luiz Fernando Martha, desenvolveu um software (FTOOL) que determina, dentre outros valores, as reações nos apoios de vigas, pórticos, quadros bidimensionais, os diagramas de esforço normal, de esforço cortante e de momento fletor. Uma ferramenta acadêmica muito difundida e um ótimo software de estruturas para modelos bidimensionais (na seção Explore + está o site que leva à versão mais nova do FTOOL (4,0), que tem a versão acadêmica, gratuita, e a profissional, com licença.).
Será realizado um exemplo já resolvido (viga biapoiada de 3 m de comprimento com carga triangular). Determinação dos esforços cortante e fletor em x = 1 m, para fins de comparação, a partir do FTOOL versão 3.1.
- Inicialmente, desenha-se a viga com o comprimento desejado.
- Depois, os apoios são vinculados à estrutura. No input, deverão ser informadas as restrições do apoio para que o software consiga identificá-los.
Por exemplo, um apoio de 2º gênero deverá apresentar as informações de restrições em x e y e rotação livre.
Observe parte da tela do FTOOL na figura a seguir, em que informações para o apoio são apresentadas.
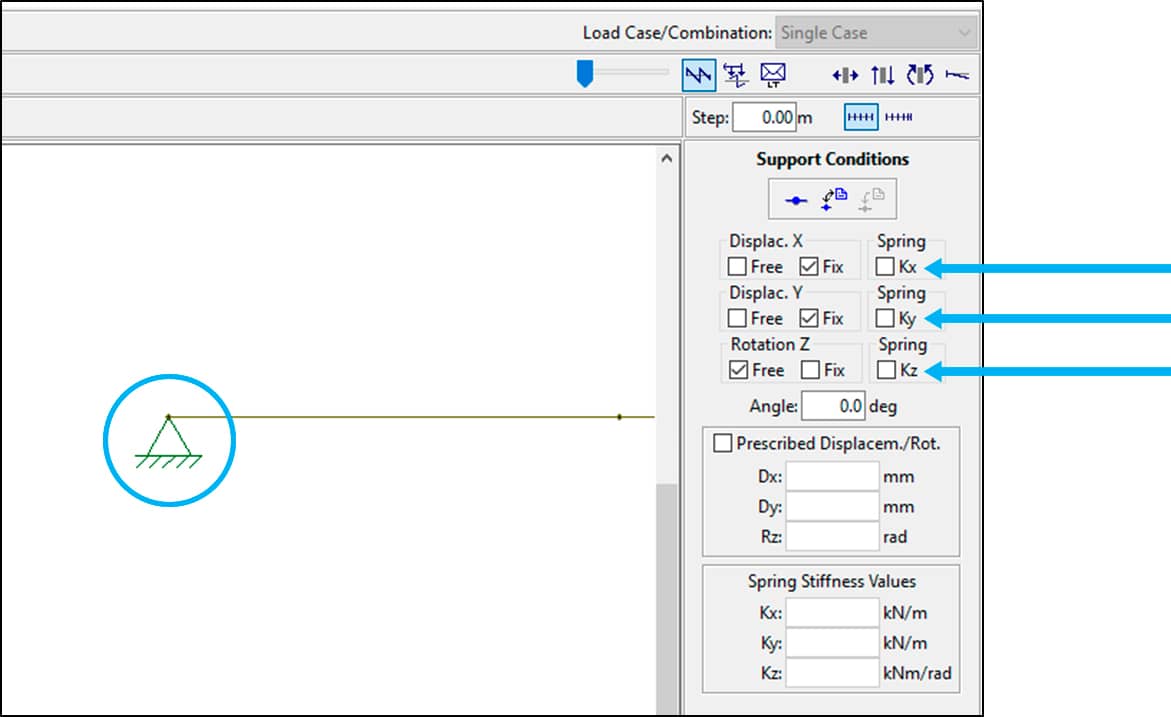
Apoios. Imagem gerada pelo FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Perceba a importância de se conhecer bem as restrições impostas pelos apoios. Nesse caso, as translações em x e y são nulas e a rotação permitida, ou ainda, trata-se de um apoio de segundo gênero.
Após a montagem da barra e o carregamento desejado, a tela para o modelo proposto no problema terá o aspecto mostrado na figura seguinte.
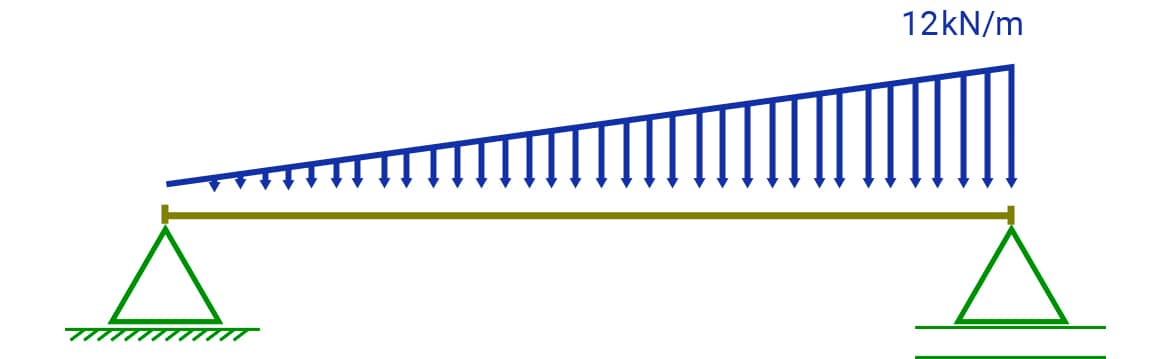
Carregamento viga biapoiada. Imagem baseada no FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Numa terceira etapa de “alimentação” do software, são necessários parâmetros geométricos da seção reta da viga (forma, dimensões etc.) e parâmetros do material que constitui a viga.
Cumprida essa etapa, os diagramas de esforço cortante e momento fletor podem ser apresentados, assim como as reações nos apoios.
Observe na figura, a seguir, o DEC, as reações nos apoios e o esforço cortante para x = 1 m afastado do apoio à esquerda.
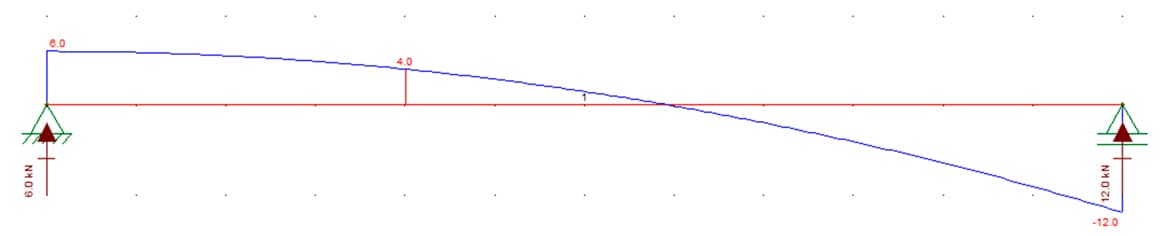
DEC e esforço cortante em x = 1 m. Imagem gerada pelo FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Na figura, a seguir, há o DMF para o exemplo proposto.
Observe o valor do momento fletor em x = 1 m. Cabe ressaltar que a convenção utilizada pelo FTOOL para o DMF é oposta a que foi adotada nesse tema, ou seja, valores positivos do momento encontram-se abaixo da viga e vice-versa.
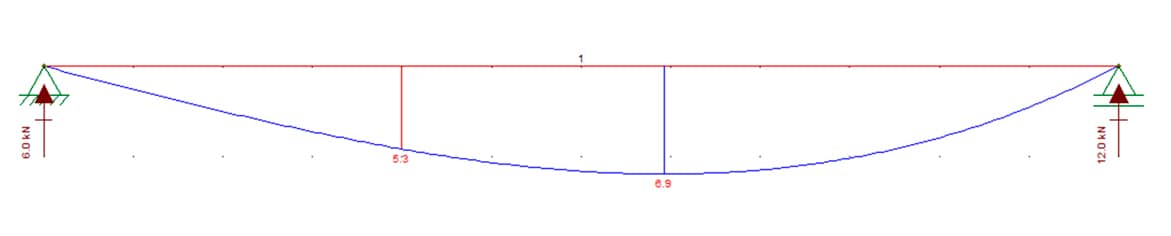
DMF e momento fletor em x = 1m. Imagem gerada pelo FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Mão na Massa
Teoria na prática
Considere uma estrutura em que parte dela apresenta uma viga biapoiada com peso próprio de 300 kN e comprimento 6 m. A 1/3 de cada apoio existe uma viga apoiada, tal que cada uma equivale a uma carga concentrada de 100 kN. Inicialmente, será feito um estudo para a criação de uma modelo físico simplificado. Duas premissas serão adotadas para a simplificação do modelo físico: a viga é isostática e homogênea. Sendo assim, os apoios são de primeiro e segundo gêneros. Uma vez que a viga é homogênea, o peso total será distribuído ao longo do comprimento, ou seja, um carregamento uniformemente distribuído de 300/6 = 50 kN/m. Dessa forma, a figura a seguir representa a modelagem física da situação apresentada.
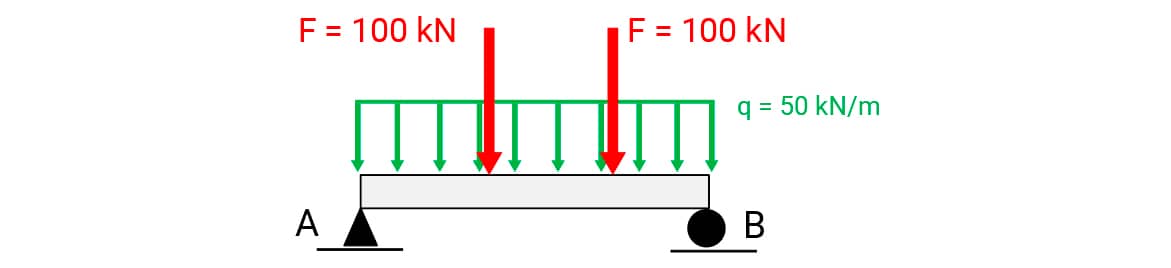
Como segunda etapa, será realizada a modelagem matemática do problema. As equações decorrem do equilíbrio estático (translacional e rotacional) do corpo rígido. Para tanto, será desenhado o DCL da viga. Substituição do carregamento distribuído por uma força concentrada.
- Intensidade: área do retângulo = 50 . 6 = 300 kN;
- Ponto de aplicação: linha de ação passando pelo centroide, ou seja, pelo ponto médio da base do retângulo (3 m).
A seguir, está o DCL da viga.
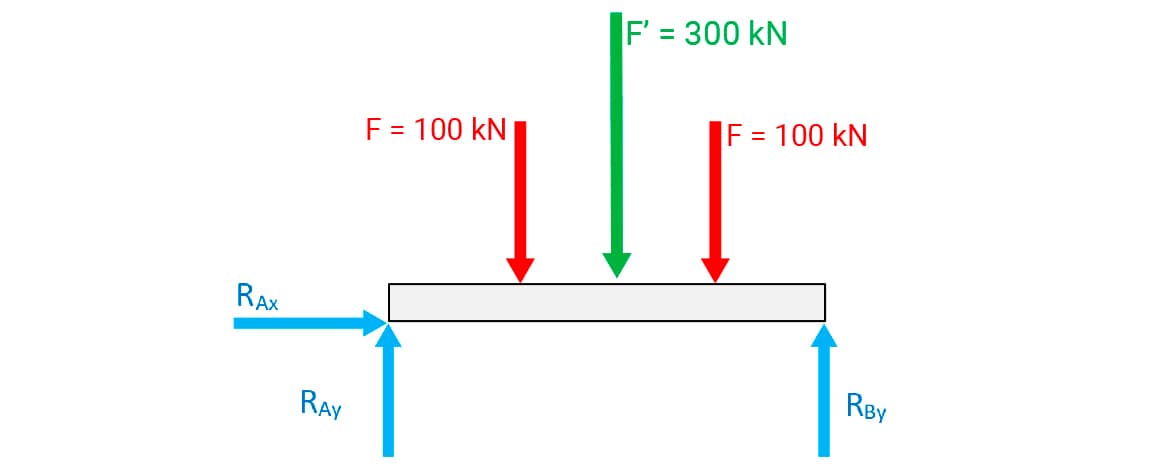
Aplicando-se as equações de equilíbrio do corpo rígido:
•
•
• (sentido anti-horário do momento positivo). Momento das forças em relação a A, tem-se
-100 . 2 – 300 . 3 – 100 . 4 + RBY . 6 = 0 (***).
Na terceira etapa, utilização da ferramenta computacional. A partir das equações (*), (**) e (***) é possível escrever o sistema de equações lineares 3 . 3.
O sistema é de fácil resolução, mas também é possível utilizar uma ferramenta computacional para este objetivo. Vários programas estão disponíveis para a resolução de sistemas lineares.
Geralmente, utilizam-se regras conhecidas como a de Cramer, a de Gauss-Jordan, a da decomposição LU etc. O aluno também pode desenvolver um programa numa linguagem de programação (C++, Python etc.) que conheça e utilizá-lo.
Aplicando uma ferramenta computacional, determinam-se RBY = 250 kN, RAY = 250 kN e RAX = 0. Para a determinação dos diagramas de esforço cortante e momento fletor (DEC e DMF) será utilizado o FTOOL.
Perceba que esse software também determina as reações, o que eliminaria a etapa anterior. Seguem os diagramas da viga.

DEC da viga. Imagem gerada pelo FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Para utilização do FTOOL, foram feitos alguns inputs (tipo de apoios, carregamentos, seção reta, propriedades do material etc.). Observe alguns detalhes no diagrama de esforço cortante (DEC). O coeficiente angular de cada reta terá valor igual a -50, que equivale a - q(x). Por exemplo, na primeira reta, o coeficiente angular será determinado por .
Similarmente, pode-se fazer para as demais retas do DEC. Nos dois pontos de aplicação das cargas concentradas, existem dois degraus cujos valores equivalem aos das intensidades das forças concentradas (150 – 50 = 100 kN). Além disso, as reações nos apoios estão mostradas no DEC.
Também utilizando a ferramenta FTOOL, é possível gerar o diagrama de momento fletor (DMF) para a viga em estudo.

DEC da viga. Imagem gerada pelo FTOOL, de autoria do prof. Luiz Fernando Martha, da PUC-RJ.
Observe que o DMF, em situações mais simplórias, pode ser rapidamente determinado a partir do DEC. Primeiramente, o DEC é representado por funções do primeiro grau (retas), assim o DMF será composto por funções do segundo grau (parábolas). A partir das áreas sob o DEC, descobre-se a variação do momento fletor no comprimento da viga analisado. Note que, no DMF, para se chegar ao valor de 400 kN.m, bastaria ter feito a área correspondente ao intervalo no DEC (área do trapézio) e a partir do zero (apoio de segundo gênero não impede rotação) traçar uma parábola. De maneira sucessiva, completa-se o DMF. Cabe ratificar que o FTOOL utiliza como convenção, no desenho do DMF, valores positivos abaixo da viga.
Assista ao vídeo Determinação do DEC e do DMF utilizando a ferramenta FTOOL
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Neste tema, apresentamos um dos elementos estruturais mais importantes utilizados na Engenharia, as vigas biapoiadas sob carregamento.
Inicialmente, fez-se uma descrição da geometria das vigas e dos carregamentos possíveis. Uma vez definida a viga e o carregamento, apresentamos os conceitos dos efeitos internos, esforço cortante V e momento fletor M.
A partir das equações do equilíbrio do corpo rígido, mostramos a técnica para determinação dos esforços internos V e M para uma seção particular da viga em estudo. Em seguida, foi possível realizar a generalização para qualquer seção da viga, isto é, determinar funções para o esforço cortante V(x) e para o momento fletor M(x).
A partir dessas equações, e com a convenção de sinais adotada, foi possível traçar os diagramas do esforço cortante e do momento fletor (DEC e DMF).
Relações matemáticas entre carregamento, esforço cortante e momento fletor foram estudadas e utilizadas.
Por fim, apresentamos a modelagem computacional das vigas biapoiadas com utilização da ferramenta FTOOL.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Identificou a geometria e os carregamentos de uma viga biapoiada isostática
Calculou os efeitos internos de flexão e cisalhamento numa viga biapoiada isostática
Esquematizou os diagramas de estado de vigas biapoiadas isostáticas
Compreendeu a modelagem computacional das vigas biapoiadas isostáticas


