Descrição

Princípios de funcionamento das máquinas síncronas. Descrição do funcionamento e da operação do gerador e do motor síncronos.

PROPÓSITO

Compreender o princípio de funcionamento das máquinas síncronas, o comportamento dos geradores sob diferentes condições de operação e o comportamento dos motores síncronos sob diferentes condições de carga.

Preparação

Antes de iniciar o conteúdo, tenha em mãos uma calculadora científica, a calculadora de seu smartphone ou computador, ou um software matemático do qual você tenha mais conhecimento.

OBJETIVOS

Módulo 1

Descrever o funcionamento do gerador síncrono sob diferentes condições de operação

Módulo 2

Descrever o funcionamento do motor síncrono sob diferentes condições de operação

MÓDULO 1

Descrever o funcionamento do gerador síncrono sob diferentes condições de operação

Introdução

As máquinas de corrente alternadas (máquinas AC) que serão estudadas neste tema são caracterizadas por possuir, em seu interior, um campo magnético que gira à mesma frequência de sua rede de alimentação. Devido a essa característica, são denominadas máquinas síncronas. As máquinas síncronas são divididas em:

  • Geradores síncronos.
  • Motores síncronos.

O funcionamento das máquinas síncronas é baseado na interação dos campos existentes no interior da máquina, cujo estudo será iniciado na próxima seção.

Campos magnéticos girantes

No interior das máquinas AC, existem dois campos: o campo do rotor e o campo do estator.

Campo do rotor (BR)

É alimentado por uma fonte de tensão DC e, ao ser posto em movimento, induzirá tensões trifásicas nos enrolamentos do estator.

Campo do estator (BS)

É formado a partir de um conjunto de correntes alternadas trifásica, de mesma amplitude e defasadas entre si de 120o, aplicadas nos enrolamentos do estator. O campo BS possui módulo constante e gira no interior da máquina com a mesma frequência da corrente que o produziu.

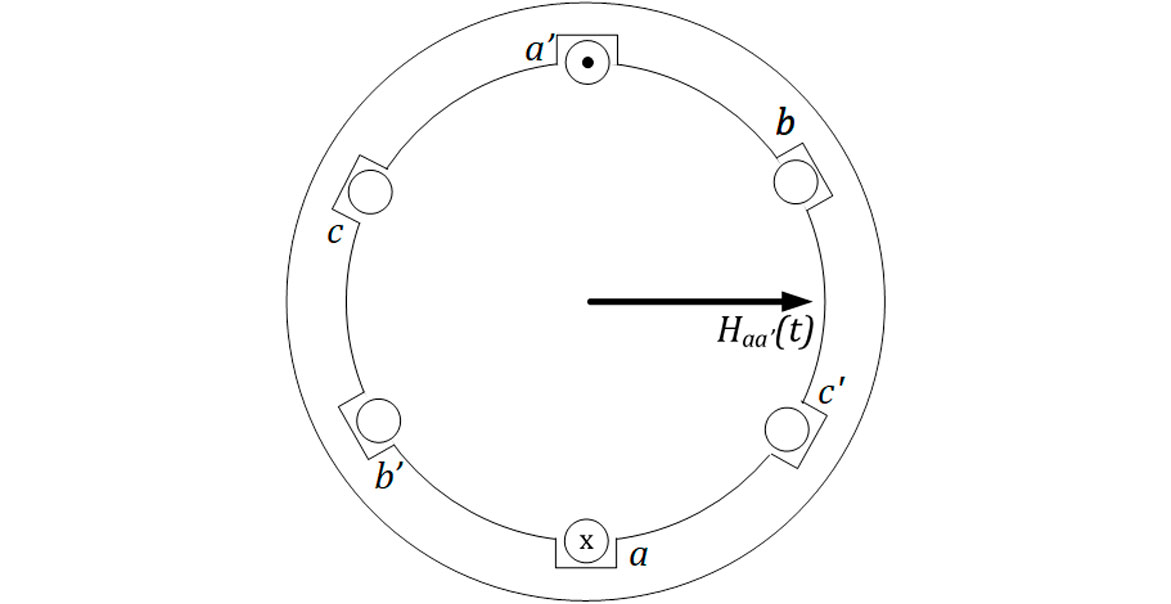
O enrolamento trifásico é formado por três enrolamentos espaçados de 120°. A partir de agora, denominaremos cada um dos enrolamentos por aa’, bb’ e cc’, que são percorridos pelas correntes da fase a, da fase b e da fase c, respectivamente. O estator da máquina e seus enrolamentos são mostrados na Figura 1.

Figura 1 – Estator da máquina e seus enrolamentos.

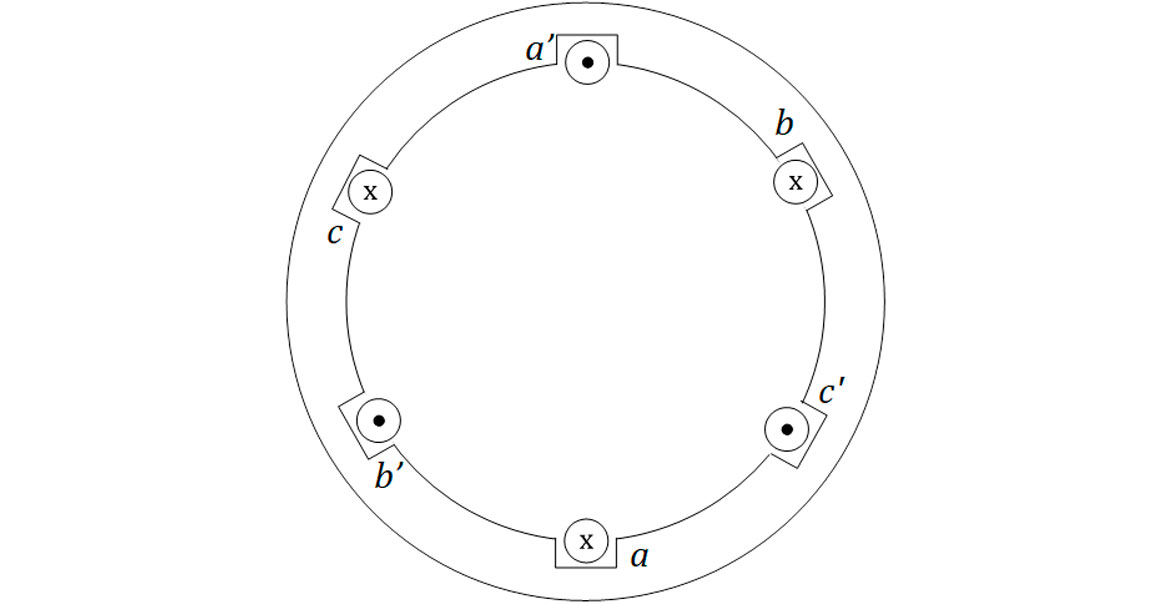
Agora, suponha que comece a circular, no enrolamento da fase a, uma corrente dada por:

i aa ' ( t )   =   I max sen ( ωt )   [ A ]                     ( 2 - 1 )

Pelo sentido indicado na Figura 2, o campo magnético Haa’ será pulsante e apontará na direção do eixo x.

Figura 2 – Campo magnético Haa’ no interior da máquina.

Agora, considere que, nos enrolamentos bb’ e cc’, sejam aplicadas as seguintes correntes:

i bb ' ( t )   =   I max sen ( ωt - 120 o )   [ A ]                   ( 2 - 2 )

i cc ' ( t )   =   I max sen ( ωt - 240 o )   [ A ]                   ( 2 - 3 )

As correntes ibb e icc produzirão os campos Hbb’ e Hcc’ no interior do estator, conforme mostra a Figura 3.

Figura 3 – Campos magnéticos no interior da máquina.

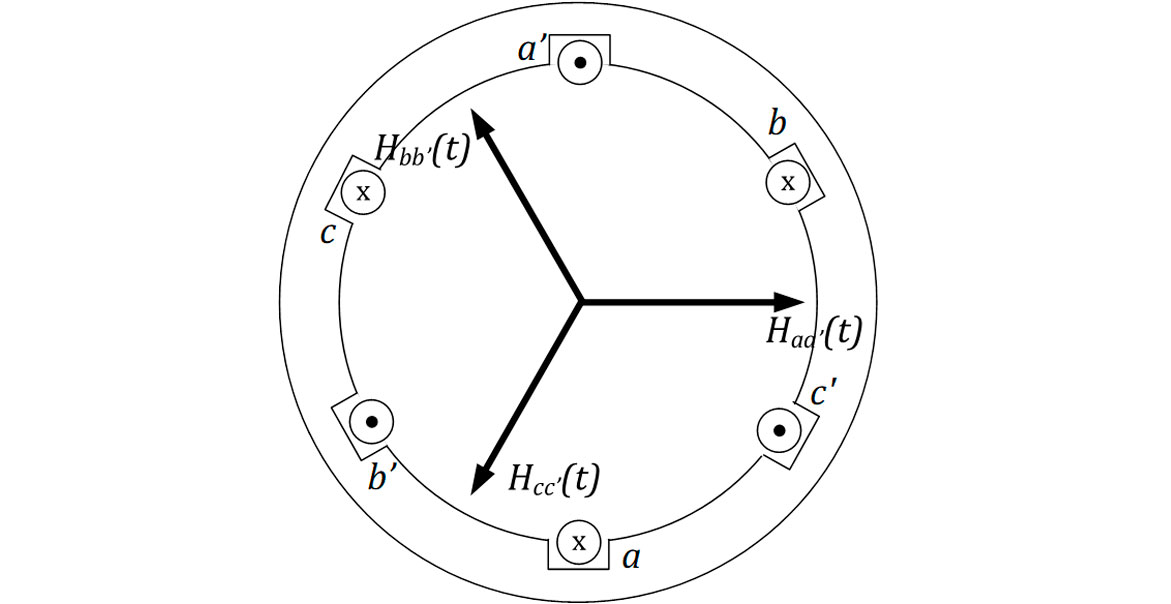
Cada um dos campos produzidos pelas correntes será pulsante e com a direção indicada por:

H aa ' ( t )   =   H max sen ( ωt ) ∠ 0 o [ A . esp / m ]                     ( 2 - 4 )

H bb ' ( t )   =   H max sen ( ωt   - 120 o ) ∠ 120 o [ A . esp / m ]                     ( 2 - 5 )

H cc ' ( t )   =   H max sen ( ωt   - 240 o ) ∠ 240 o [ A . esp / m ]                     ( 2 - 6 )

Sabendo-se que B = μH, podemos multiplicar ambos os lados das equações: 2-4, 2-5 e 2-6 por μ,e obter:

B aa ' ( t )   =   B max sen ( ωt ) ∠ 0 o   [ T ]                     ( 2 - 7 )

B aa ' ( t )   =   B max sen ( ωt - 120 ) ∠ 120 o   [ T ]                     ( 2 - 8 )

B cc ' ( t )   =   B max sen ( ωt - 240 ) ∠ 240 o   [ T ]                     ( 2 - 9 )

Podemos comprovar que o campo resultante no interior do estator, denominado Bs, é a soma dos campos produzidos por cada uma das correntes, e seu módulo será constante e igual a uma vez e meia a densidade de campo máxima, e girará com a frequência da rede, conforme mostrado na Equação 2-10.

B s ( t ) = B aa ' ( t ) + B bb ' ( t ) + B cc ' ( t ) = 1 , 5 max sen ( ωt ) i → - 1 , 5 B max cos ( ωt ) j →                     ( 2 - 10 )

O efeito desse campo magnético girante no interior do estator é equivalente à existência dos polos norte e sul de um imã girando no interior do estator com a frequência igual à da rede, conforme mostra a Figura 4.

Figura 4 – Campos magnético resultante (Bs) no interior do estator.

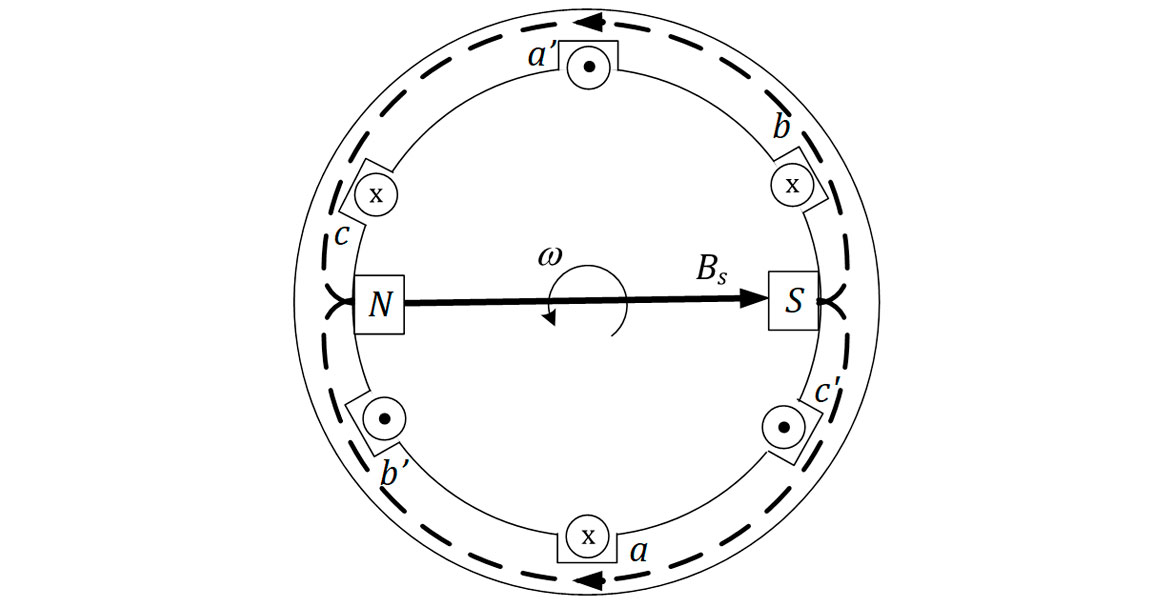
Os polos completarão uma volta ao redor do estator no intervalo de tempo correspondente a Δt = 1 /fe, em que fe é a frequência elétrica da rede. Nesse caso, dizemos que:

f e = f m                     ( 2 - 11 )

f m é a frequência mecânica de giro da máquina síncrona.

Ou, em termos de velocidade angular, podemos escrever:

ω e = ω m                     ( 2 - 12 )

ω m é a frequência angular mecânica de giro da máquina síncrona.

Agora, considere que o padrão do estator seja duplicado, conforme a Figura 5.

Figura 5 – Estator da máquina com dois enrolamentos por fase.

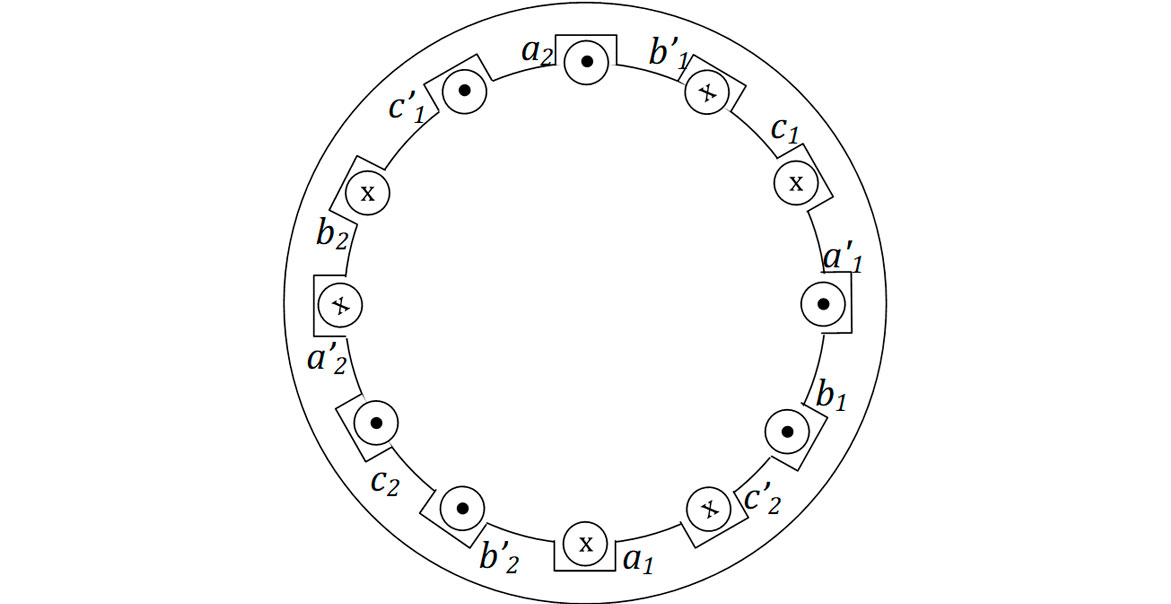
O efeito da inclusão do novo enrolamento é o equivalente à inclusão de mais dois polos no estator, de acordo com a Figura 6.

Figura 6 – Estator da máquina 4 polos girantes.

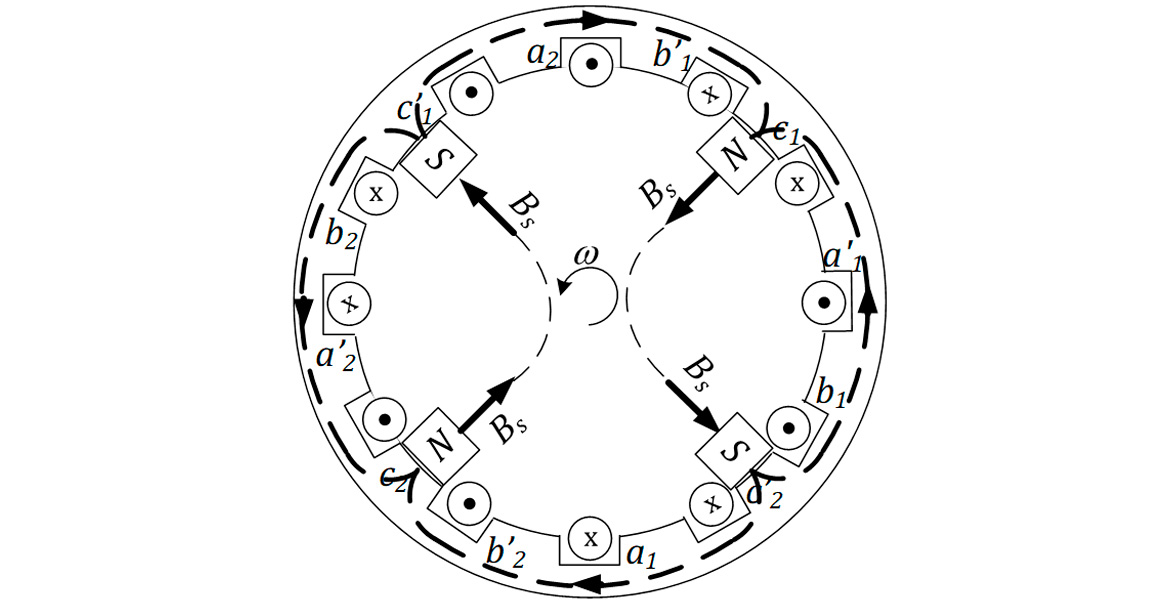
Nessa nova configuração, podemos perceber que são necessários 90° mecânicos para que sejam percorridos 180° elétricos (sair de um polo norte e chegar em um polo sul), ou seja:

θ e = 2 θ m                     ( 2 - 13 )

Essa relação também pode ser expandida para a velocidade angular, que será:

ω e = P 2 ω m                     ( 2 - 14 )

P é o número de polos girantes no entreferro.

Entreferro

Espaço reduzido de ar, ou o seu equivalente em material não magnético, através do núcleo de uma bobina, transformador ou outro dispositivo magnético.

Usualmente, a velocidade a rotação da máquina é dada em rotação por minuto (rpm), então, a frequência mecânica poderá ser dada por:

f m = n m 60                     ( 2 - 15 )

  • f m é dada em hertz.
  • n m é a frequência mecânica em rotações por minuto e é dada em rpm.

Diante do exposto, a velocidade de rotação do campo do estator, em rpm, poderá ser dada por:

n m = 120 f e P                     ( 2 - 16 )

Tensão induzida na máquina

Na seção anterior, vimos que um conjunto de correntes alternadas no estator produz um campo magnético girante no interior da máquina. Agora, veremos como um campo magnético girante produzirá tensão induzidas nos enrolamentos do estator.

Considere a espira abcd, apresentada na Figura 7. A espira possui raio r, comprimento L e está posicionada no estator da máquina.

Figura 7 – Espira no estator da máquina.

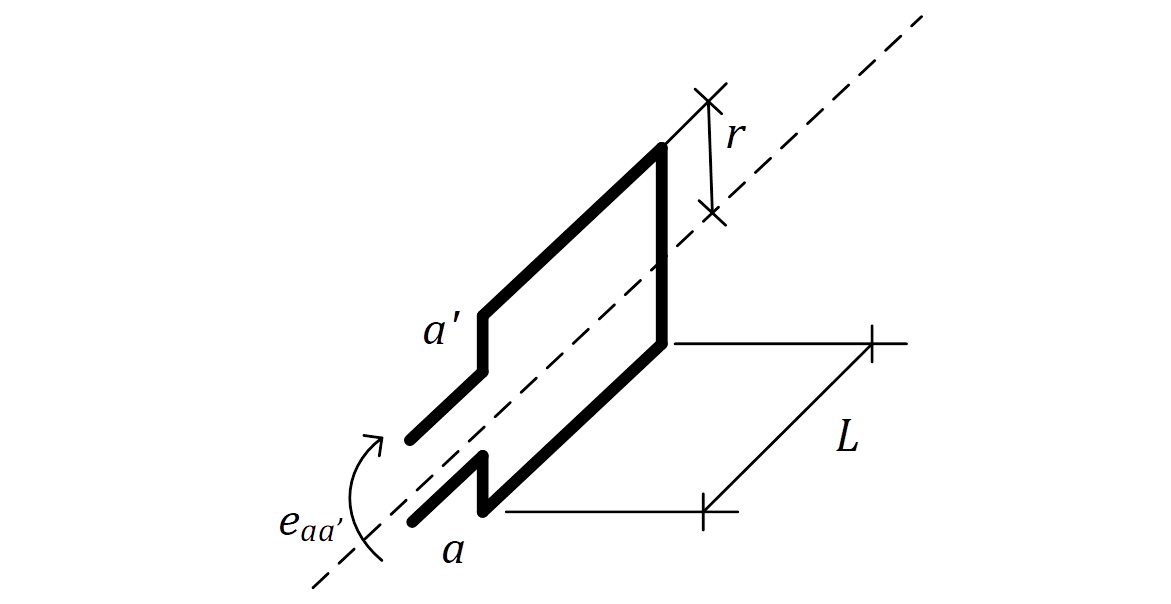
No rotor da máquina, encontra-se instalado o circuito de campo, que produzirá o campo do rotor BR, que girará em uma velocidade ω . Decompondo-se BR nas direções dos eixos x e y, teremos:

B R = B Rx i → + B Ry j → = B R cos ( ωt ) i →   +   B R sen ( ωt ) j →                     ( 3 - 1 )

Figura 8 – Campo no interior da máquina.

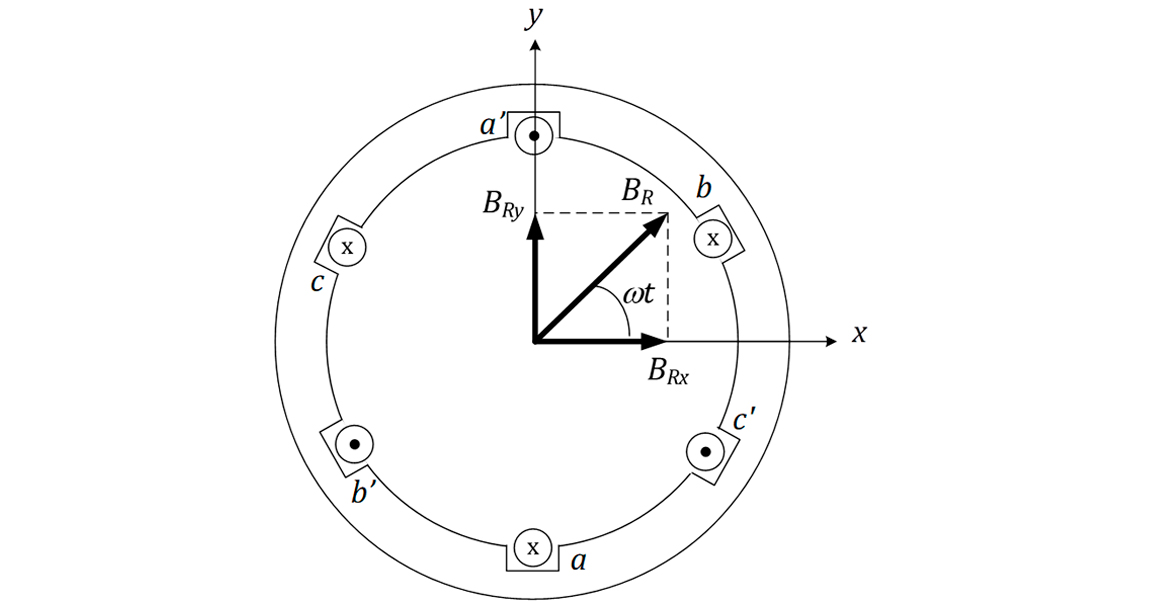
No entanto, como BRy está no plano da máquina, sua variação ao longo do tempo não induzirá tensão na espira. Somente a variação do campo BRx será responsável por induzir tensão, cujo valor é:

e ind ( t ) = e aa ' ( t ) = - dϕ dt = - dB Rx A dt = - 2 rL dB Rx dt = - 2 rL d dt ( B R cos ( ωt ) ) e aa ' ( t ) =   2 rLB R ωsen ( ωt )
(3-2)

Sabendo-se que ϕ = 2 rLB R , a Equação 3-2 pode ser reescrita como:

e aa ' ( t ) = ϕωsen ( ωt )                     ( 3 - 3 )

Considerando-se que o enrolamento da fase a tenha N espiras, a Equação 3-3 pode ser escrita da seguinte forma:

e aa ' ( t ) = Nϕωsen ( ωt )   [ V ]                   ( 3 - 4 )

Analisando-se a Equação 3-4, verificamos que a tensão induzida na máquina AC depende das suas características construtivas, do fluxo e da velocidade da máquina.

Expandindo-se esse raciocínio para os demais enrolamentos, podemos concluir que as tensões induzidas nos enrolamentos terão a mesma amplitude, mas estarão defasadas de 120° entre si, conforme indicado a seguir:

e bb ' ( t ) = Nϕωsen ( ω m t - 120 o )   [ V ]                   ( 3 - 5 )

e cc ' ( t ) = Nϕωsen ( ω m t - 240 o )   [ V ]                   ( 3 - 6 )

A tensão máxima induzida no enrolamento, Ea, é dada por: E a = Nϕω .

E, como ω = 2πf, temos que:

E a = 2 πfNϕ                     ( 3 - 7 )

E o valor eficaz da tensão será:

E eficaz = 2 πfNϕ 2 = 2 πfNϕ                     ( 3 - 8 )

A tensão, cujo valor eficaz acabamos de calcular, é denominada tensão de fase. A tensão terminal do gerador dependerá da forma como ele está conectado:

delta (Δ)

Se a ligação dos enrolamentos for em delta (Δ):

V t = E eficaz

estrela (Y)

Se a ligação dos enrolamentos for em estrela (Y):

V t = 3 E eficaz

O torque em máquinas AC

Durante a sua operação, dois campos magnéticos estão presentes no interior da máquina:

  • Campo magnético do rotor.
  • Campo magnético do estator.

Durante o seu funcionamento, esses campos tentarão se alinhar e produzirão o torque no interior da máquina.

Agora, vamos determinar esse torque.

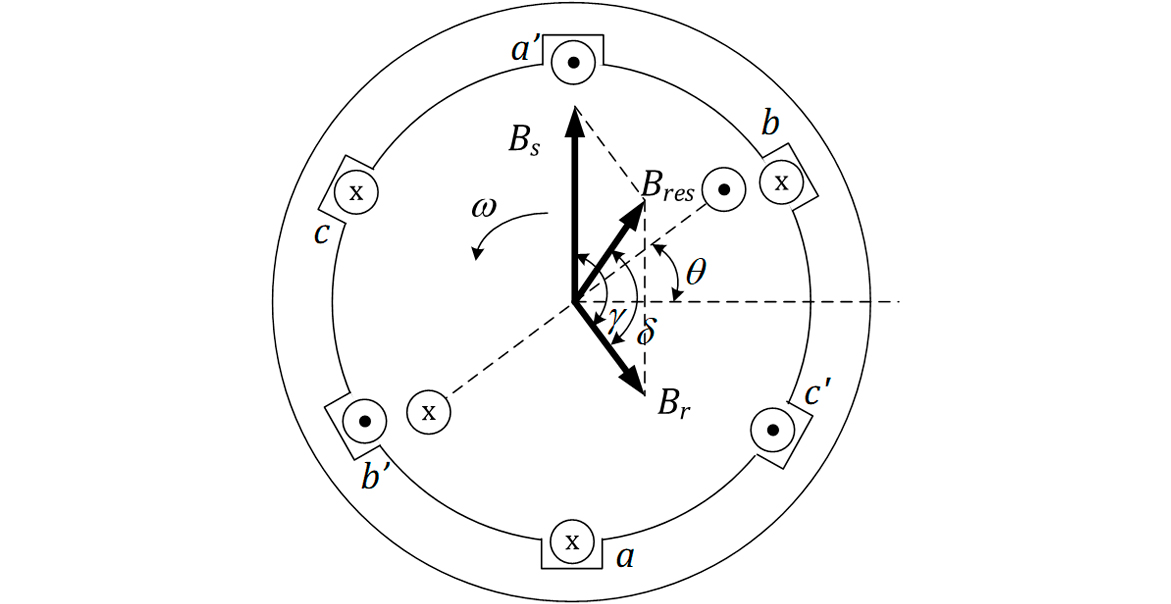
Considere que o rotor da máquina esteja girando na velocidade síncrona e que, em dado instante, a sua posição seja a mostrada na Figura 9. Primeiramente, considere que o campo magnético produzido pela corrente do rotor BR, seja proporcional à corrente do rotor, ou seja:

B R = αI R                     ( 4 - 1 )

E que o campo girante do estator seja proporcional à corrente do estator, de acordo com a expressão a seguir:

B S = βI S                     ( 4 - 2 )

Considere, ainda, que a defasagem entre BS e BR seja γ. Da análise da Figura 9, verificamos que:

γ = 180 ° - θ                     ( 4 - 3 )

Sabemos que o torque induzido pelos campos BS e BR será:

τ ind = kB R × B S                     ( 4 - 4 )

Mas:

B res = B R + B s                       ( 4 - 5 )

Logo:

τ ind = kB R × ( B res - B R ) = kB R × B res = kB R B res sen ( δ )                     ( 4 - 6 )

Observando a Figura 9, verificamos que o torque induzido está no sentido de rotação do rotor, portanto, nessa situação, a máquina funciona como um motor:

Figura 9 – Campos no interior da máquina AC.

Funcionamento do gerador síncrono

Considere que uma corrente contínua é aplicada aos enrolamentos do rotor. Essa corrente fará surgir o campo do rotor BR. Ao ser posto em rotação por uma fonte de energia mecânica externa, o campo BR girará no interior da máquina, induzindo tensões trifásicas nos enrolamentos de cada uma das fases, conforme apresentado no item: O torque em máquinas AC.

Nas máquinas AC, existem dois tipos de rotor:

Polos salientes

Comumente usados em turbinas hidráulicas, operam na vertical, a baixas rotações ( < 1800 rpm) e possuem número de polos maior de quatro.

Polos lisos

Comumente usados em geradores acionados por turbinas a vapor, operam na horizontal, a altas rotações ( > 1800 rpm) e possuem dois ou quatro polos.

Em função da forma de excitação do circuito de campo, os geradores podem ser:

Com escovas e anéis

A fonte DC para a alimentação do circuito de campo é fornecida por escovas.

Sem escovas (brushless)

Um pequeno gerador AC fornece tensão ao circuito de campo que se encontra instalado no rotor. Essa tensão alternada induzida no rotor será retificada para ser empregada no circuito de campo.

Atenção

Para o desenvolvimento dos modelos dos geradores e motores síncronos deste Tema, serão considerados os geradores com rotores de polos lisos e em regime permanente.

Rotores de polos lisos

Nestes rotores, o entreferro é constante e ininterrupto ao longo de toda a periferia do núcleo de ferro.

Já vimos que a velocidade de rotação da máquina é dada por:

n m = 120 f e P                     ( 5 - 1 )

E sabemos que a tensão induzida é proporcional às características construtivas da máquina, ao fluxo e à velocidade da máquina, de acordo com a expressão:

E a = kϕn                   ( 5 - 2 )

Então, da mesma forma em que foi feito nas máquinas DC, devemos levantar a curva de magnetização das máquinas AC, mostrada na Figura 10. Para que se obtenha a curva de magnetização, o gerador deverá ser acionado à velocidade constante e sem nenhuma carga conectada aos seus terminais (operação em vazio), em seguida, a sua corrente de campo deverá ser variada e, para cada um desses valores, a tensão nos terminais da máquina precisará ser medida.

Figura 10 – Curva de magnetização da máquina AC.

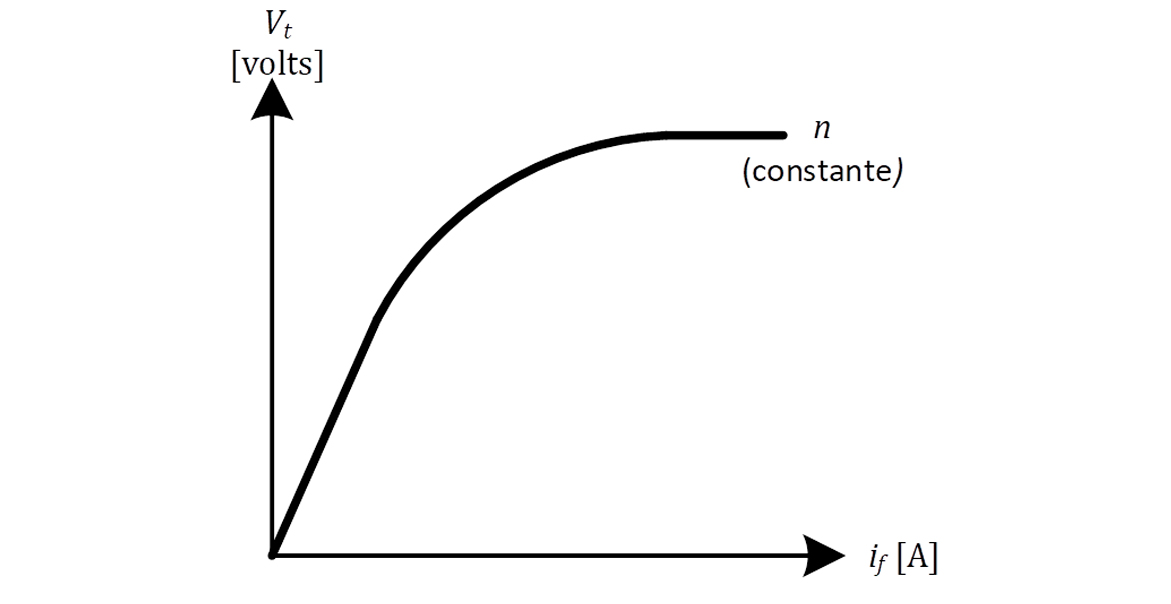
Atenção

Atente para o seguinte ponto!

Como não há corrente no gerador, não há queda de tensão em sua impedância interna e, portanto, o valor da tensão induzida dependerá da forma como ele está ligado.

Para ligação em delta:

V t = E a         ( 5 - 3 )

Para ligação em estrela, a tensão terminal será maior do que a tensão induzida:

V t = 3 E a             ( 5 - 4 )

Agora, quando há corrente no gerador, a sua tensão terminal será influenciada pelos seguintes fatores:

1 Alteração do campo magnético interno devido ao efeito de reação da armadura.
2 Autoindutância da bobina dos enrolamentos da armadura.
3 Resistência da bobina dos enrolamentos da armadura.

Para compreender o efeito de reação de armadura na máquina, considere um rotor de dois polos girando no interior da máquina. Esse rotor induzirá tensões nos enrolamentos de cada uma das fases. Ou seja, o campo do rotor Br induzirá tensões Ea nos enrolamentos das fases, tensões essas defasadas em 120° entre si. Como não há carga, não haverá queda de tensão na impedância interna da máquina e a sua tensão terminal dependerá da forma como ela foi ligada (Equações 5-3 e 5-4).

Figura 11 – Campo do rotor BR e tensão induzida EA na máquina AC.

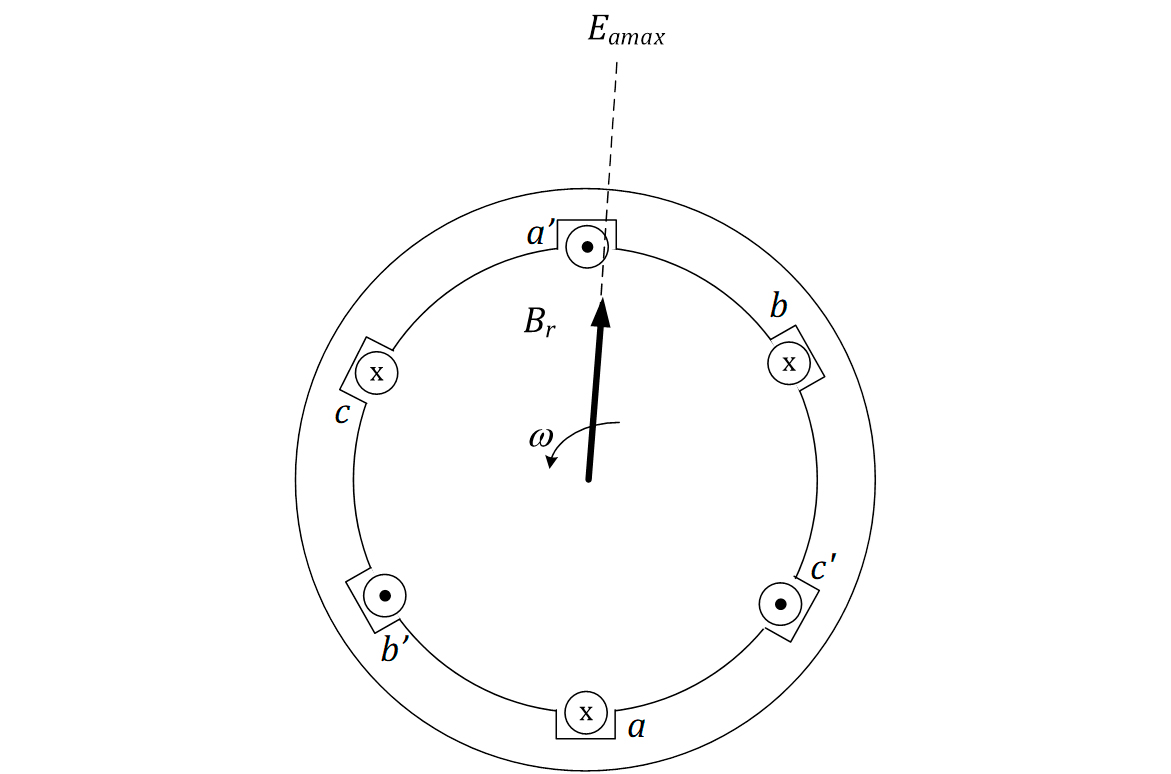
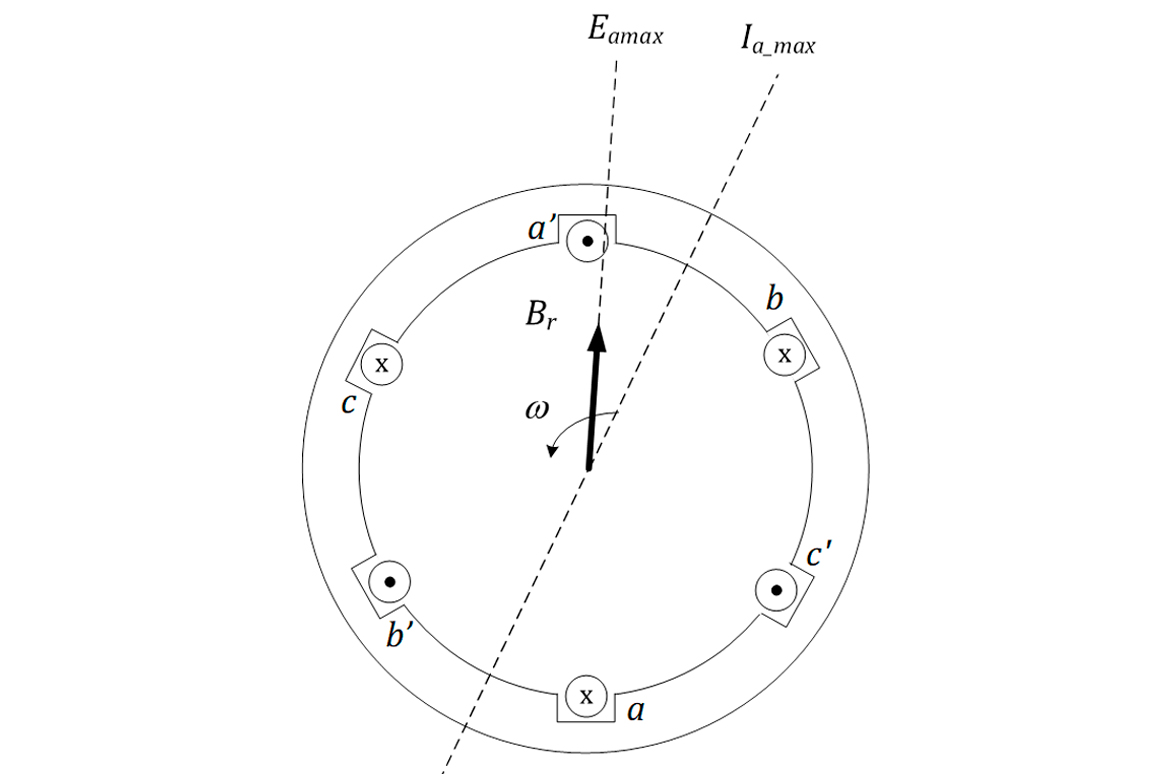
Considere, agora, que uma carga trifásica indutiva seja conectada aos terminais do gerador. A corrente ficará defasada da tensão, conforme a Figura 12. Essa corrente produzirá o campo do estator BS, segundo a Figura 13. Da mesma forma que o campo BR, o campo BS induzirá tensões nos enrolamentos da armadura, denominada Eestator. A tensão de fase, finalmente, será a soma da tensão induzida Ea e a Eestator, ou seja:

V ϕ = E a + E estator                   ( 5 - 5 )

E, no interior da máquina, conforme apresenta a Figura 14, o campo resultante, Bres será:

B res = B R + B s                     ( 5 - 6 )

Figura 12 – Correte de armadura IA máquina AC.
Figura 13 – Campo BS produzida pela corrente IA.
Figura 14 – Campos no interior da máquina.

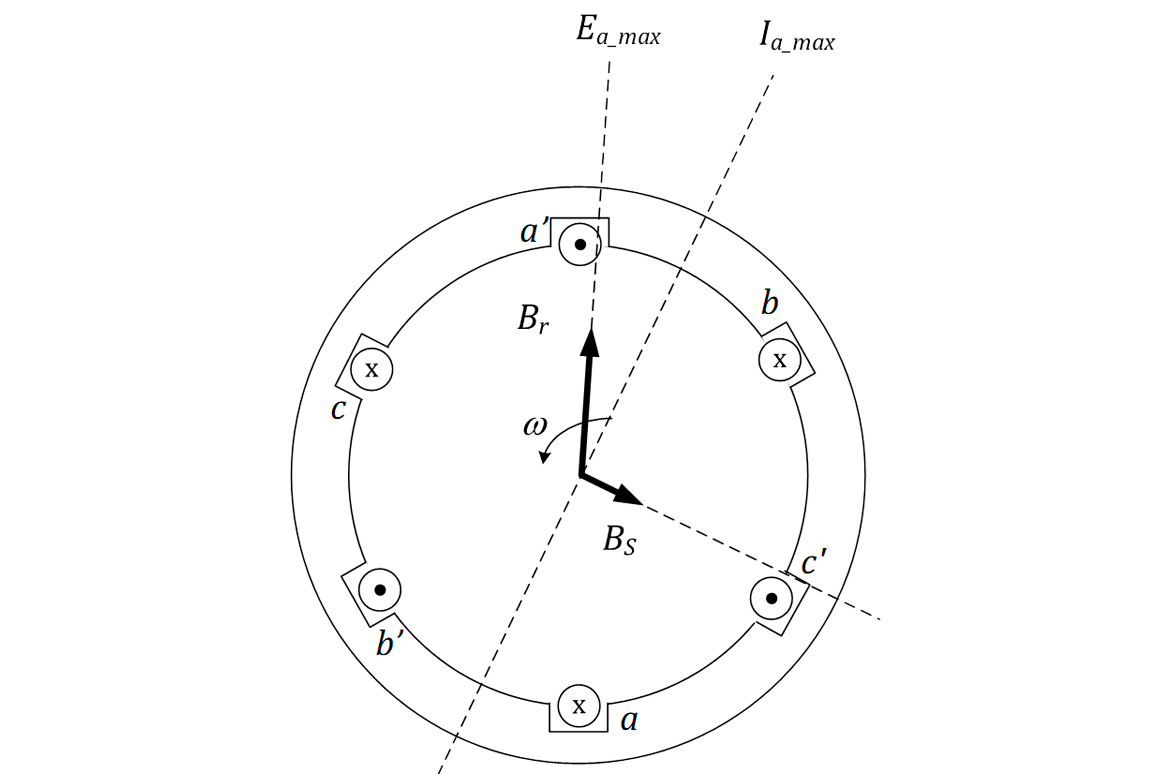
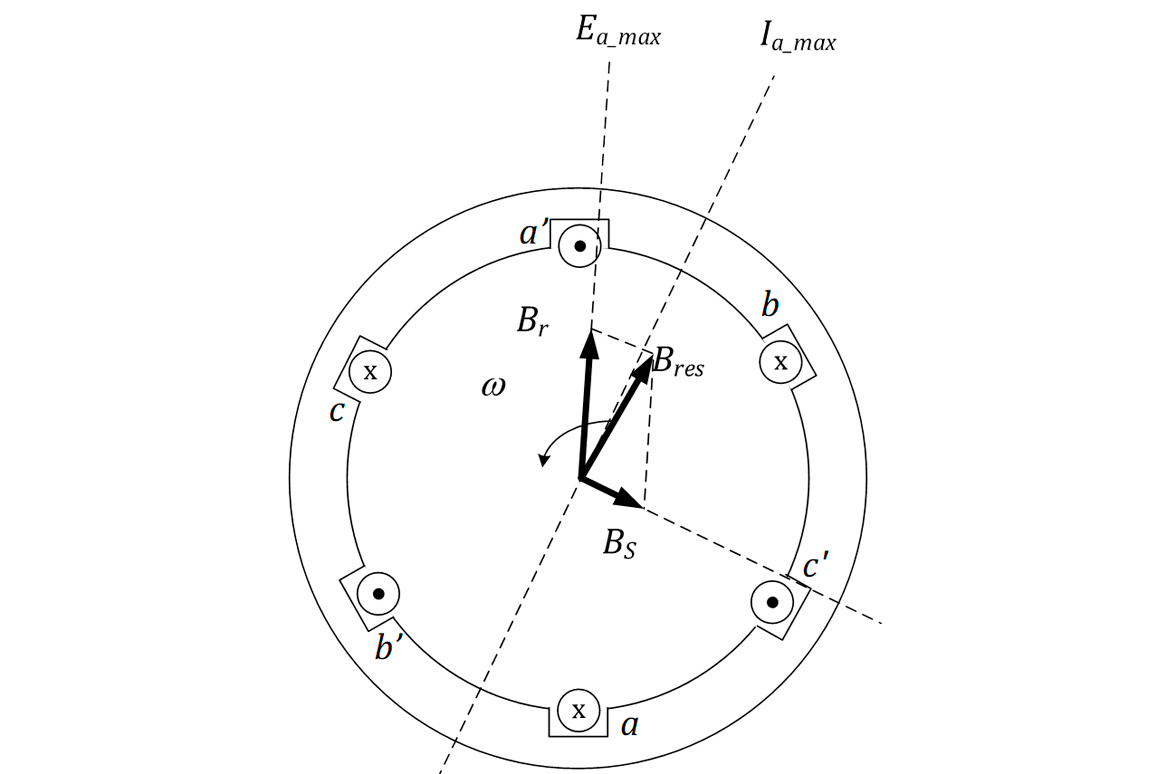
Repare que o campo do estator BS é proporcional à corrente de armadura IA e que ele está atrasado noventa graus em relação à corrente IA. Como Bs gera a Eestator, a tensão do estator pode ser representada por:

E estator = - j X I a                     ( 5 - 7 )

  • - j é a constante necessária para atrasar o campo do estator 90o em relação à corrente de armadura.
  • X é a constante de proporcionalidade que representa a reatância indutiva das bobinas de armadura.

Agora, aplicando 5-7 em 5-5, teremos:

V ϕ = E a - jXI a                     ( 5 - 8 )

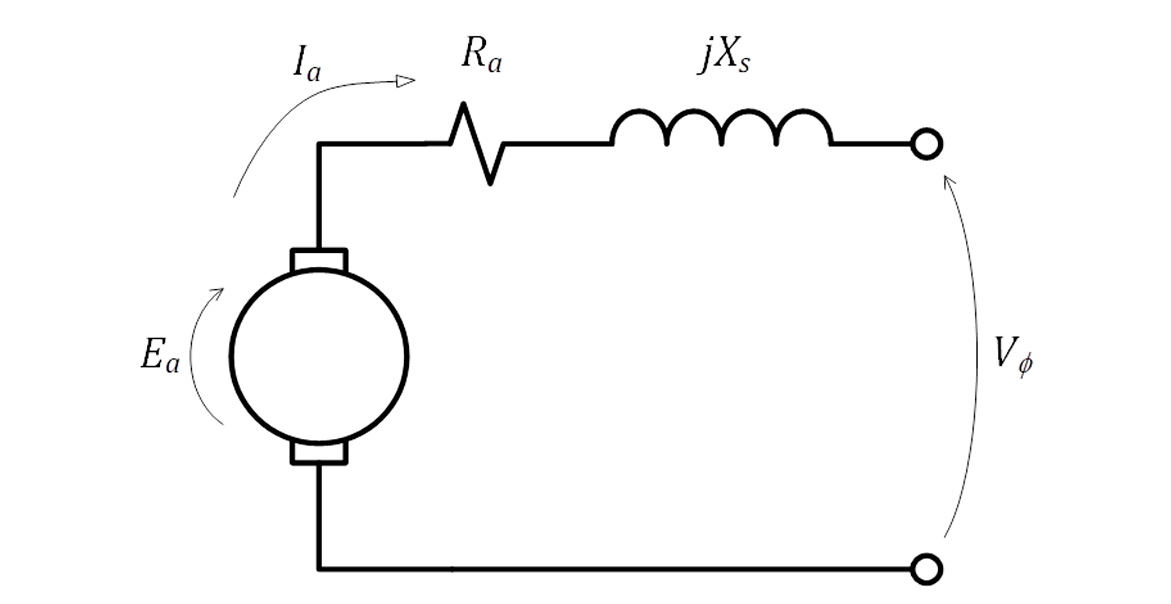
Entretanto, além do efeito da reação de armadura, as bobinas possuem indutância própria (La) e resistência (Ra) própria, e a nova equação de fase será:

V ϕ = E a - jXI a - jX a I a - R a I a                     ( 5 - 9 )

Chamaremos de reatância síncrona Xs a soma da reatância em função do efeito de reação de armadura e a reatância própria máquina, ou seja:

X s = X + X a                     ( 5 - 10 )

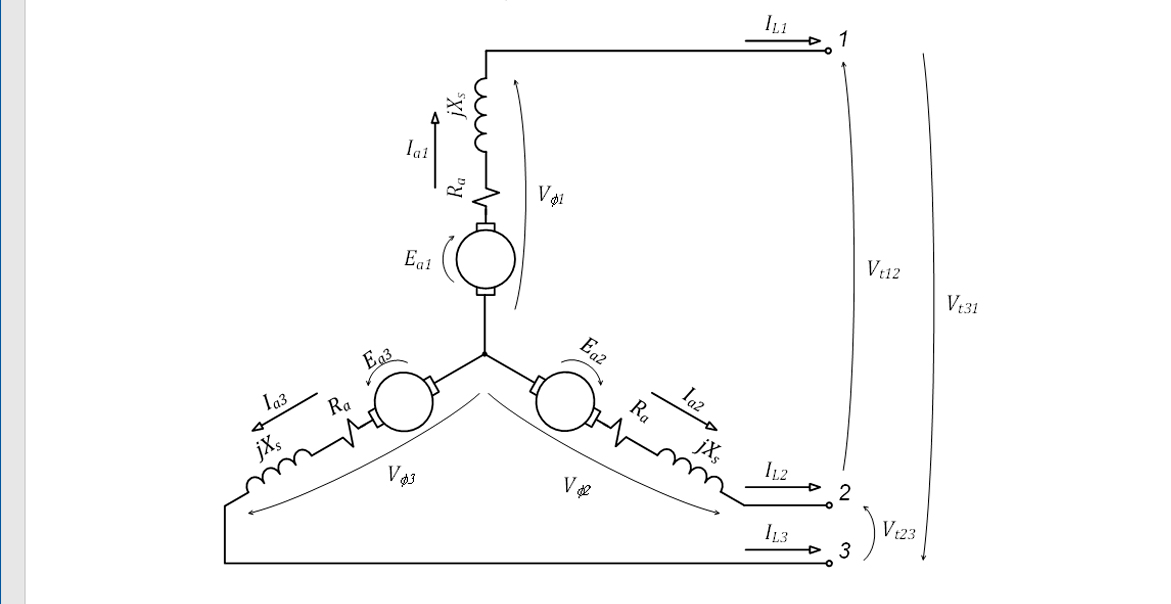
Finalmente, o circuito equivalente monofásico do gerador é mostrado na Figura 15.

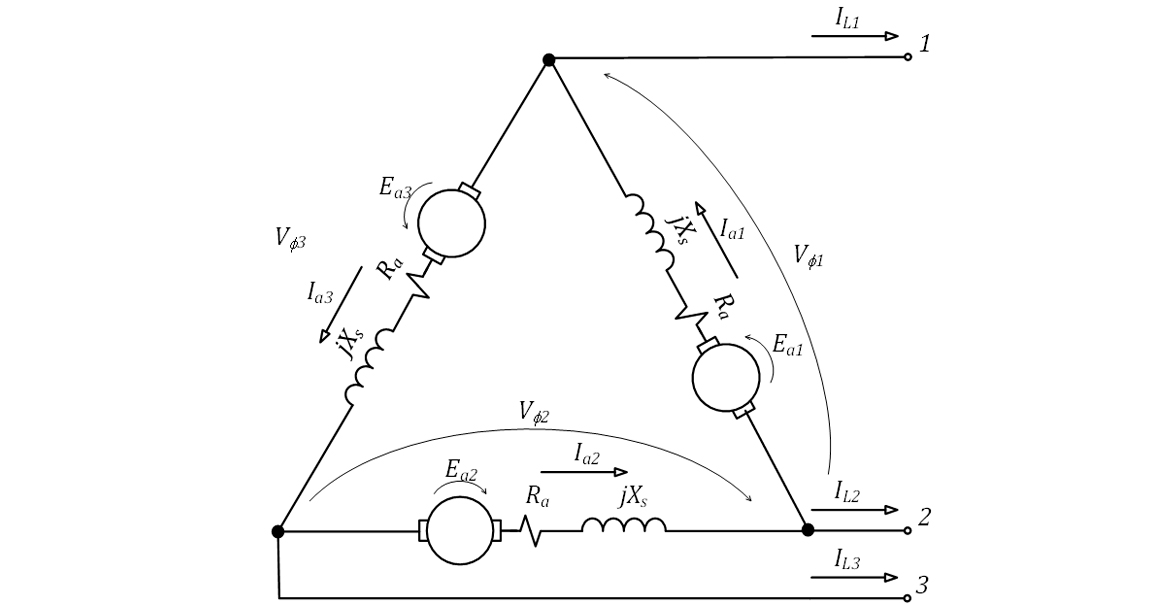
Figura 15 – Equivalente monofásico do gerador.

Agora, dependo da ligação dos enrolamentos das fases, teremos os seguintes arranjos para os circuitos:

Clique nas setas para ver o conteúdo. Objeto com interação.

Gerador ligado em estrela (Y)

Nesse tipo de ligação, tem-se:

  • Tensão induzidas de fase: E a 1 ,   E a 2     e   E a 3 ;
  • Tensões de fase: V ϕ 1 ,   V ϕ 2   e   V ϕ 3 ;
  • Tensões terminais: V t 12 ,   V t 23     e   V t 31 ;
  • Correntes de armadura (ou de fase): I a 1 ,   I a 2   e   I a 3 ;
  • Correntes de linha: I L 1 ,   I L 2     e   I L 3 .

E as suas relações são:

| V t | = 3 | V ϕ |

I L = I a

Gerador ligado em delta (Δ)

Nesse tipo de gerador, temos as mesmas tensões e correntes do gerador, mas com as seguintes relações:

| V t | = | V ϕ |

I L = 3 I a

As tensões e correntes no gerador são grandezas alternadas e são expressas, usualmente, na forma fasorial. Para a representação do diagrama fasorial, a tensão de fase V ϕ é usada como referência. As figuras 18a, 18b e 28c mostram os diagramas fasoriais para o gerador atendendo cargas resistivas, indutivas e capacitivas, respectivamente. O ângulo δ , que é o ângulo de defasagem entre a tensão induzida e a tensão de fase, é chamado de ângulo de carga.

Figura 18 – Diagramas fasoriais do gerador.

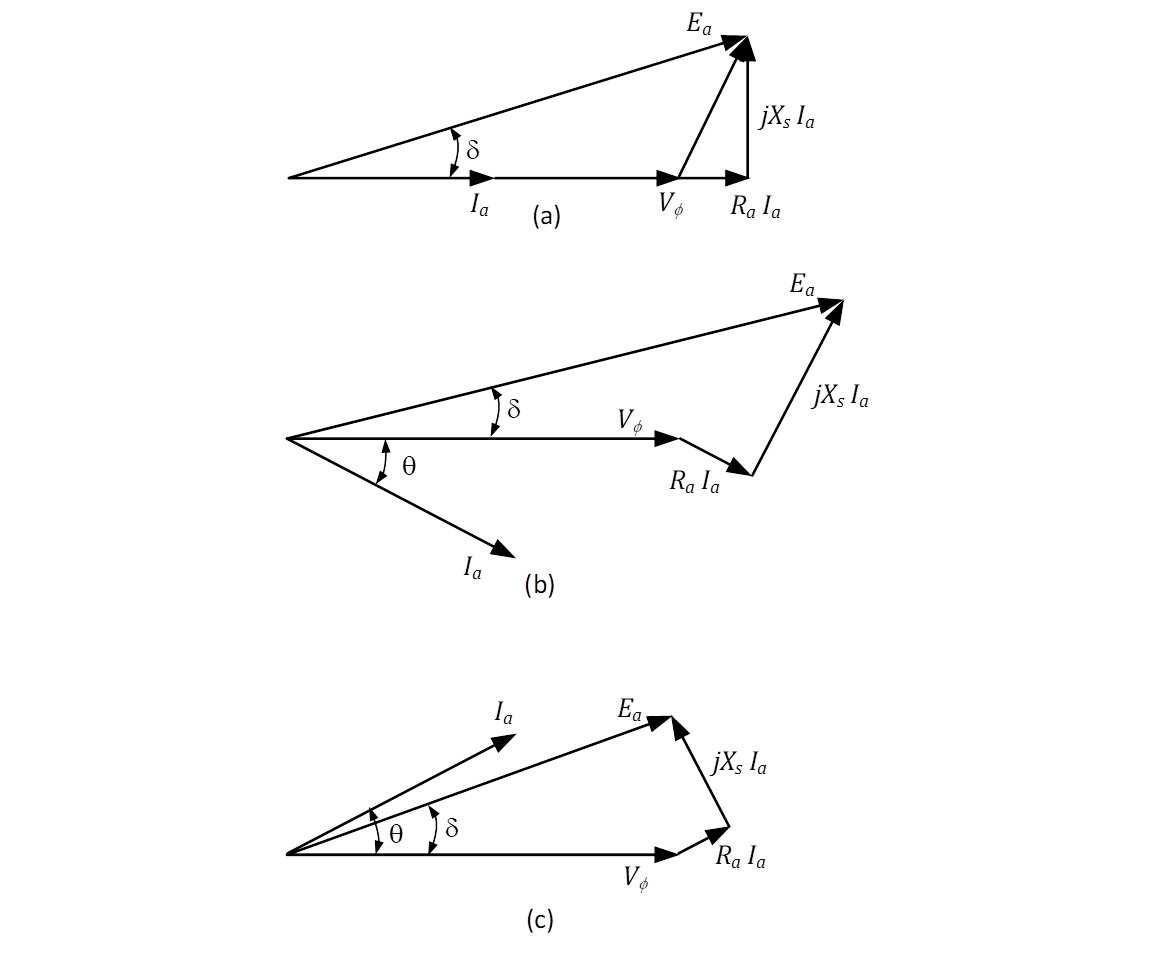
Considerando constante a velocidade de rotação do gerador, verificamos nos diagramas fasoriais que, para atender cargas resistivas e indutivas, é necessária uma corrente de campo maior para produzir uma maior tensão induzida.

Agora, o fluxo de potência do gerador é apresentado na figura abaixo.

Figura 19 – Fluxo de potência do gerador.

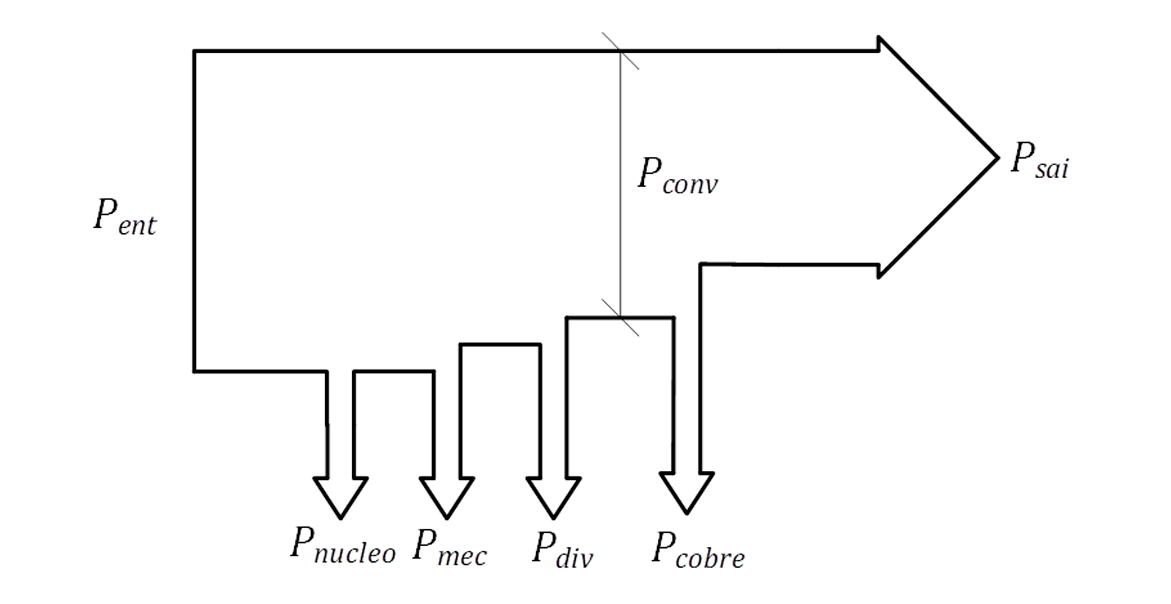
Em que a potência de entrada é dada por:

P e n t = τ a p l ω m                     ( 5 - 11 )

Em seguida, temos a perda de potência em função das perdas diversas, mecânicas e do núcleo. Abatidas essas perdas, teremos a potência convertida, que é dada por:

P c o n v = τ i n d ω m                     ( 5 - 12 )

A potência convertida é a potência elétrica disponibilizada pelo induzido, então, a potência convertida por ser reescrita da seguinte forma:

P conv = τ ind ω m = 3 E a I a cos ( γ )                         ( 5 - 13 )

γ é a defasagem entre a tensão induzida e a corrente de armadura.

As perdas no cobre do estator são dadas por:

Pcobre=3RaIA2          (5-14)

E, finalmente, teremos a potência elétrica de saída, que é dada por:

P saida = 3 V ϕ I a cos ( θ ) = 3 V L I L cos ( θ )                     ( 5 - 15 )

A potência reativa por ser expressa pelas seguintes formas:

Q saida = 3 V ϕ I a sen ( θ ) = 3 V L I L sen ( θ )                     ( 5 - 16 )

Em estudos qualitativos de máquinas AC, costuma-se desprezar a resistência de armadura. Desprezando-se a resistência de armadura, temos o diagrama fasorial mostrado na Figura 20.

Figura 20 – Diagrama fasorial com a resistência de armadura desprezada.

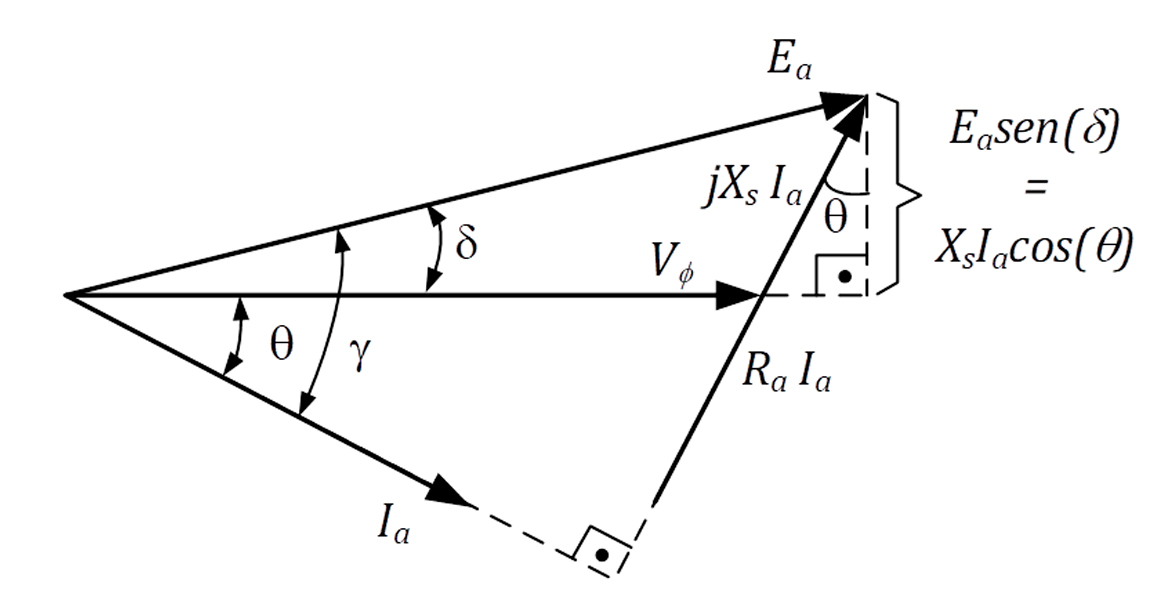
Do diagrama, verificamos que:

I a X s cos ( θ ) = E a sen ( δ )                         ( 5 - 17 )

Multiplicando-se os dois termos da 5-17 por 3 V ϕ , e divindo-os por Xs, temos a expressão que nos fornece a potência de saída do gerador:

P = 3 V ϕ I a cos ( θ ) = 3 E a V ϕ sen ( δ ) X s                     ( 5 - 18 )

δ é o ângulo de defasagem entre a tensão induzida e a tensão de fase.

E o torque induzido da máquina é dado por:

τ i n d = 3 V ϕ E a s e n ( δ ) ω m X s                     ( 5 - 19 )

Definição dos parâmetros do gerador

Para que seja possível realizar os estudos do gerador, é necessário levantar as seguintes características:

Curva de magnetização do gerador

Reatância síncrona.

Resistência de armadura.

Ensaio em vazio

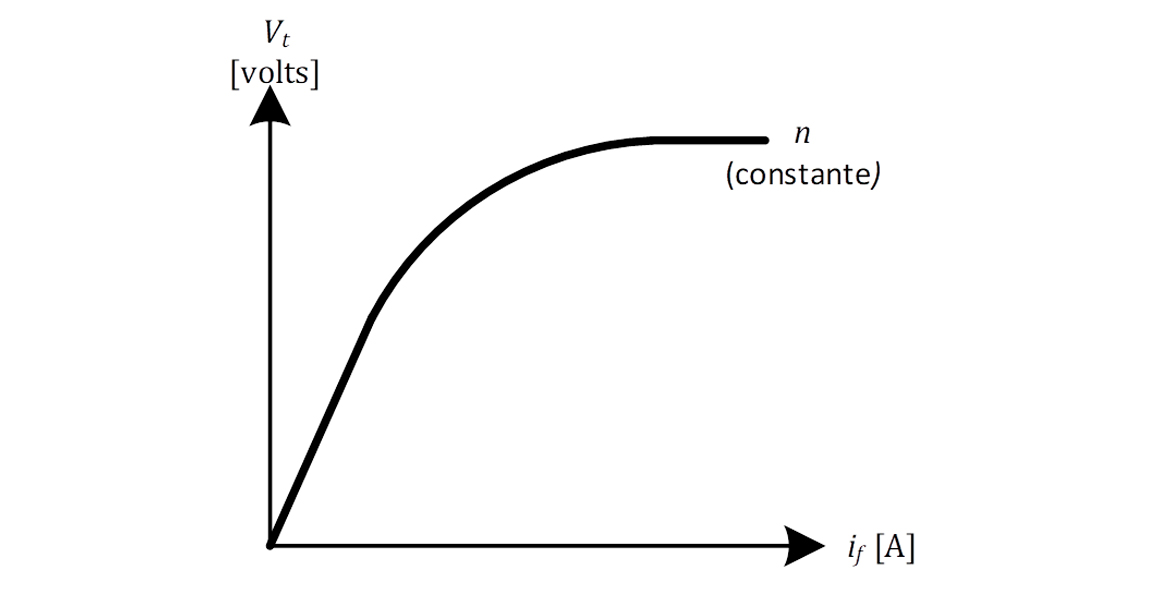
A curva de magnetização é levantada por meio do ensaio em vazio. O ensaio em vazio consiste em acionar a máquina com velocidade nominal, sem cargas conectadas aos seus terminais e com a corrente de campo igual a zero. Na sequência, aumenta-se a corrente de campo em degraus e, para cada um de seus valores, registra-se o valor da tensão terminal da máquina, levantando-se a curva de magnetização (ou característica em vazio) da máquina, de acordo com a Figura 21.

Outro ponto a se destacar desse ensaio é que, como o gerador não fornece potência elétrica de saída em seus terminais e não há perdas nas resistências de armadura, toda a potência mecânica aplicada ao gerador será usada para suprir as perdas rotacionais, por atrito, ventilação e do núcleo. .

Figura 21 – Curva de magnetização da máquina AC.

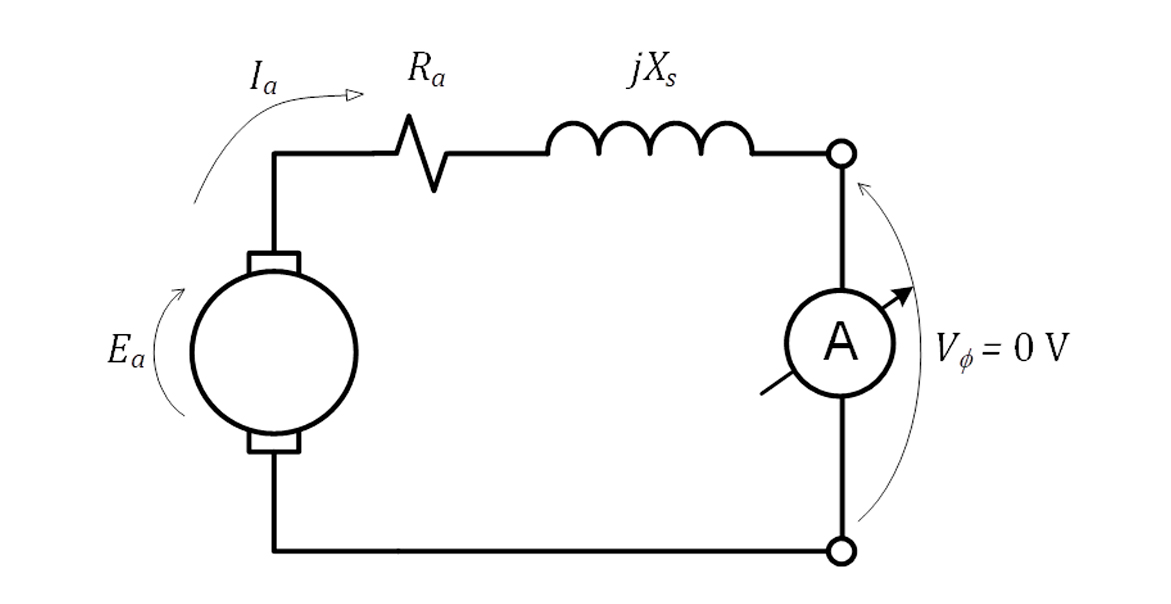
Ensaio em curto circuito

Para realizar o ensaio de curto-circuito, deve-se curto-circuitar os terminais do gerador com amperímetros, conforme mostrado no equivalente monofásico da Figura 22. Em seguida, deve-se aumentar, gradativamente, a corrente de campo até que circule corrente nominal nos terminais da máquina.

Figura 22 – Equivalente monofásico do ensaio de curto-circuito.

Como os terminais da máquina estão curtos-circuitados, temos V ϕ = 0 , e a corrente de armadura será dada por:

I a = E a R a + jX s                     ( 6 - 1 )

E seu módulo será:

Ia=EaRa2+Xs2          (6-2)

Como X s ≫ R a , temos:

X s ≈ E a I a                     ( 6 - 3 )

Como a curva de magnetização do gerador está na faixa linear, haja vista que uma pequena corrente de campo é necessária para produzir a tensão induzida, o gráfico I a × I f será linear, conforme a Figura 23.

Figura 23 – Curva característica de curto-circuito.

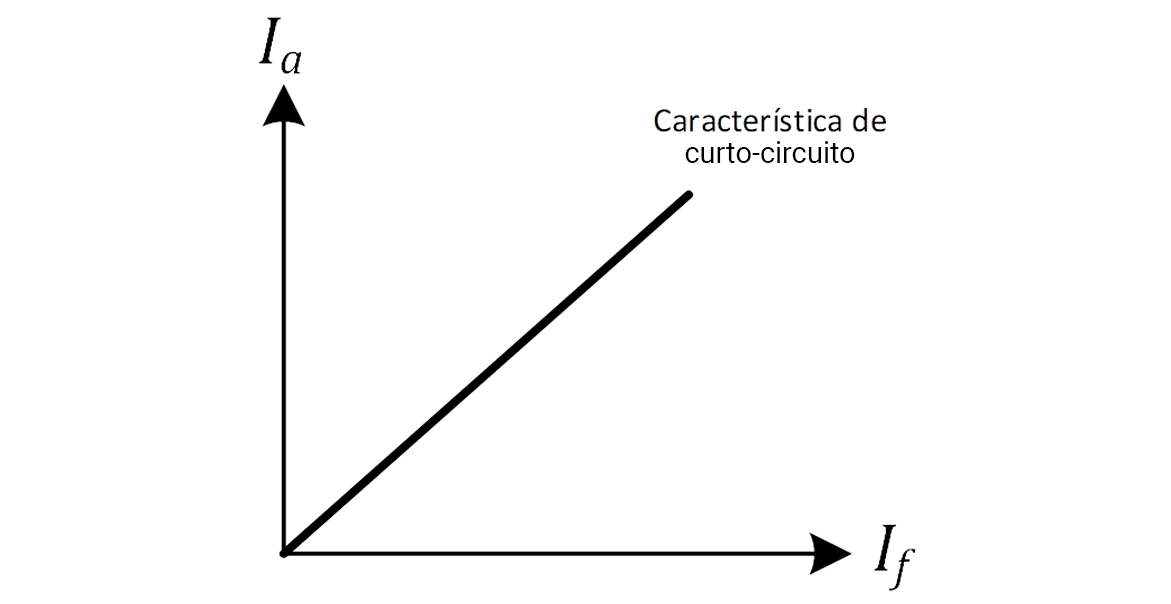
Assim, uma forma para se determinar a reatância síncrona é:

1) Do ensaio em vazio, determina-se a tensão induzida da máquina para dado valor de corrente de campo.

2) Do ensaio em curto-circuito, determina-se a corrente de armadura da máquina para o mesmo valor de corrente de campo do item 1.

3) Finalmente, o valor da reatância síncrona será obtido pela Equação 6-3.

Determinação da resistência de armadura

Para a determinação da resistência da armadura, é preciso deixar o gerador parado – dessa forma, a tensão induzida será zero – e aplicar uma tensão DC variável em dois terminais do gerador.

Atenção

A fonte de tensão deve ser ajustada até o momento em que começa a circular corrente nominal nos terminais do gerador.

Assim, com as leituras de tensão e corrente, determinamos o valor da resistência de armadura. O esquemático do circuito para a determinação da resistência de armadura é apresentado na Figura 24.

Figura 24 – Determinação da resistência de armadura para o gerador ligado em Δ.

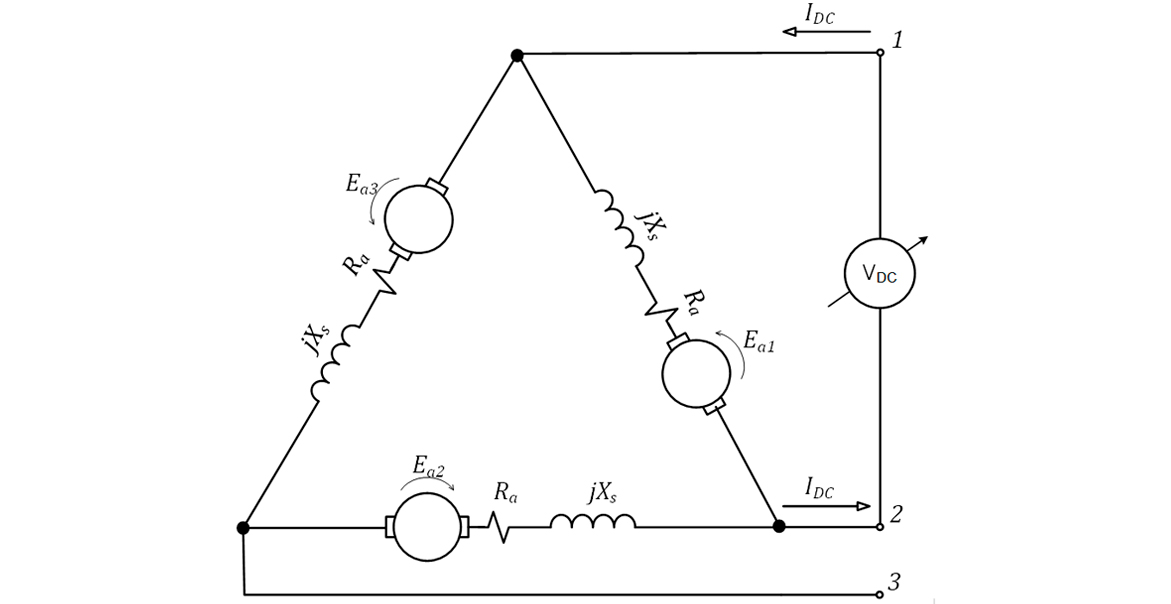
Nota-se que, para cada tipo de ligação do gerador, a expressão para o cálculo da resistência de armadura será diferente. Para o caso do gerador da figura anterior, o valor da resistência de armadura será:

R a = 3 V DC 2 I DC                     ( 6 - 4 )

Gerador sob condições de carga variável

Quando um gerador opera sozinho, ele é o responsável por atender a potência ativa e potência reativa demandada pela carga.

Comentário

Em todas as situações a serem apresentadas, a menos que se explicite o contrário, a velocidade do gerador e a corrente de campo serão constantes.

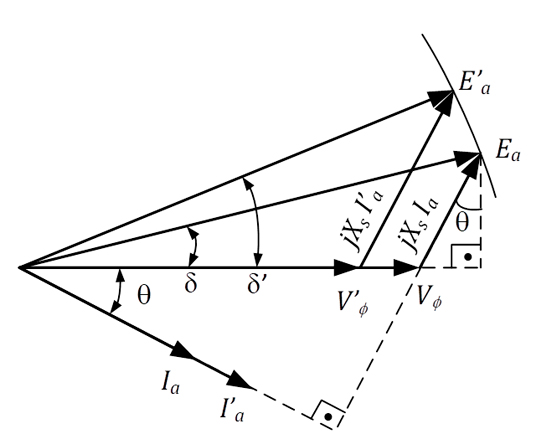
Agora, suponha que um gerador atenda uma carga que demanda uma corrente Ia com determinado fator de potência. Considere que, em dado instante, há um aumento da corrente demandada pela carga, que passa a ser I ’ a   (mantido o fator de potência), ou seja, há um aumento de potência ativa solicitada ao gerador. Com o aumento da corrente de carga, há um aumento da queda de tensão na reatância síncrona. Como não houve variação do módulo da tensão induzida (velocidade do gerador e corrente de campo mantidas constantes), o diagrama fasorial deverá fechar com o somatório da tensão de fase e da queda de tensão na reatância síncrona em um lugar geométrico onde o módulo da tensão induzida é o mesmo da situação original.

Tal lugar geométrico é obtido traçando-se uma circunferência de raio EA, segundo a Figura 25. No novo ponto de operação, pode-se perceber que a tensão terminal da máquina diminuiu e o ângulo de defasagem entre a tensão induzida e a tensão de fase aumentou, ficando de acordo com a Equação 5-18.

Agora, analise o comportamento do gerador para as variações de cargas resistivas e capacitivas.

Relação frequência X potência e tensão X reativos

Os principais mecanismos para acionar os geradores são:

Turbinas a vapor

Máquinas a diesel

Turbinas a gás

Turbinas hidráulicas

A despeito da fonte de energia, os geradores tendem a apresentar o mesmo comportamento, ou seja, quando há um aumento da potência solicitado ao gerador, a sua velocidade diminui.

Saiba mais

Essa característica do gerador é chamada estatismo ou speed drop (do inglês, queda de velocidade).

O estatismo é dado por:

SD = n em_carga - n em_carga n em_carga × 100 %                     ( 8 - 1 )

Em que n é a velocidade nominal de giro do gerador

Mecanismos de controle permitem que a velocidade em vazio da máquina seja controlada.

Agora, da relação entre a velocidade da máquina e a potência fornecida, temos a seguinte expressão:

P = s p ( f em_vazio - f sis )                     ( 8 - 2 )

  • P é a potência de saída do gerador
  • f em_vazio é a frequência em vazio do gerador
  • f sis é a frequência do sistema
  • s p é a declividade da reta, em kW/hz ou MW/hz

O gráfico da Equação 8-2 é mostrado a seguir.

Figura 26 – Curva frequência versus potência ativa.

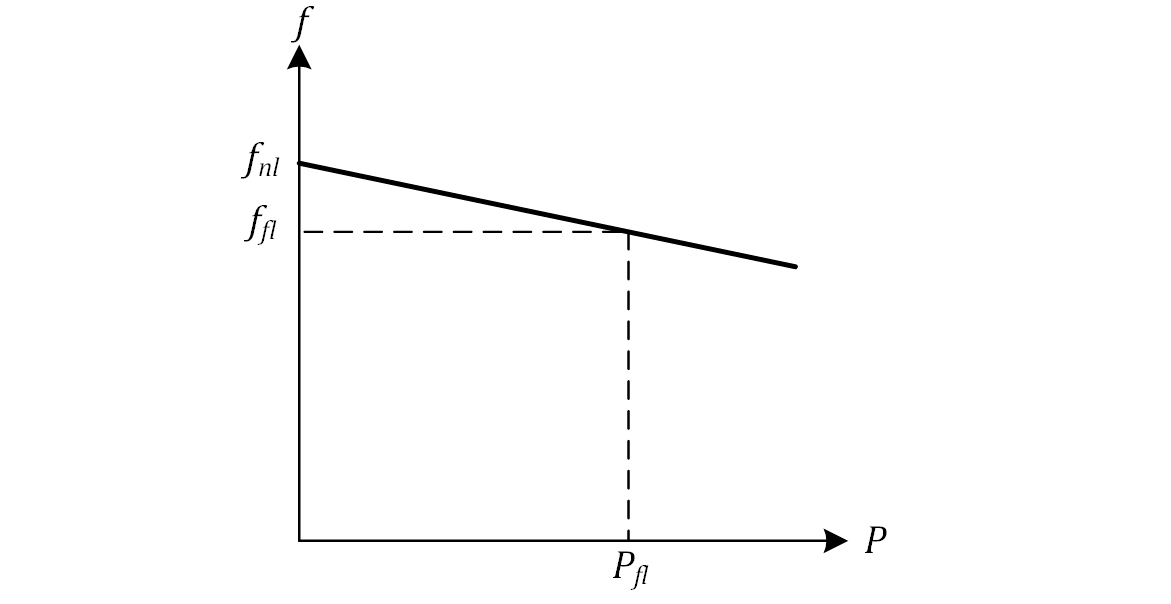
De forma semelhante ao que ocorre com a velocidade terminal, o aumento de potência reativa solicitada ao gerador faz com que sua tensão terminal caia, e o gráfico desse comportamento é indicado a seguir.

Figura 27 – Curva tensão terminal versus potência reativa.

Agora, considere que o gerador operará em paralelo com um sistema elétrico de potência (SEP).

A principal característica do SEP é que, independentemente da carga a ele solicitada, sua tensão terminal e frequência permanecem constantes.

Suponha que, inicialmente, o gerador forneça uma potência ativa ao SEP. Em dado momento, faz-se necessário aumentar a potência ativa fornecida por esse gerador. Como não houve aumento de velocidade de acionamento do gerador nem da corrente de campo, o módulo da tensão induzida é constante. Portanto, para suprir esse aumento da potência ativa, a corrente de carga vai se tornando mais capacitiva e o gerador começará a consumir reativos da rede. O diagrama fasorial da Figura 28 apresenta esse comportamento do gerador.

Figura 28 – Aumento de potência ativa do gerador.

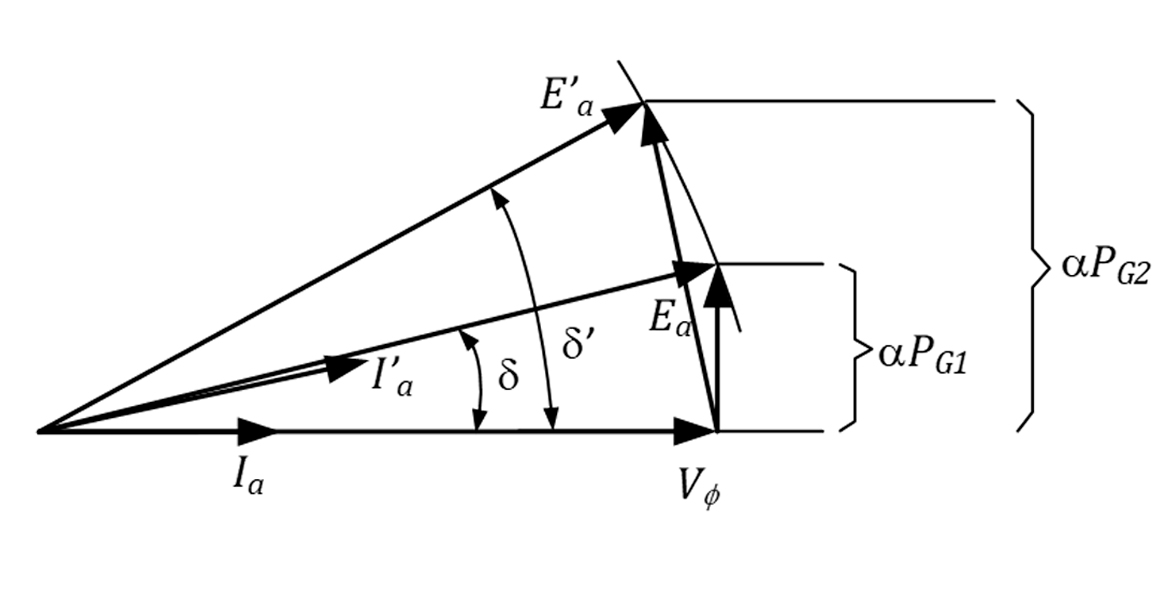
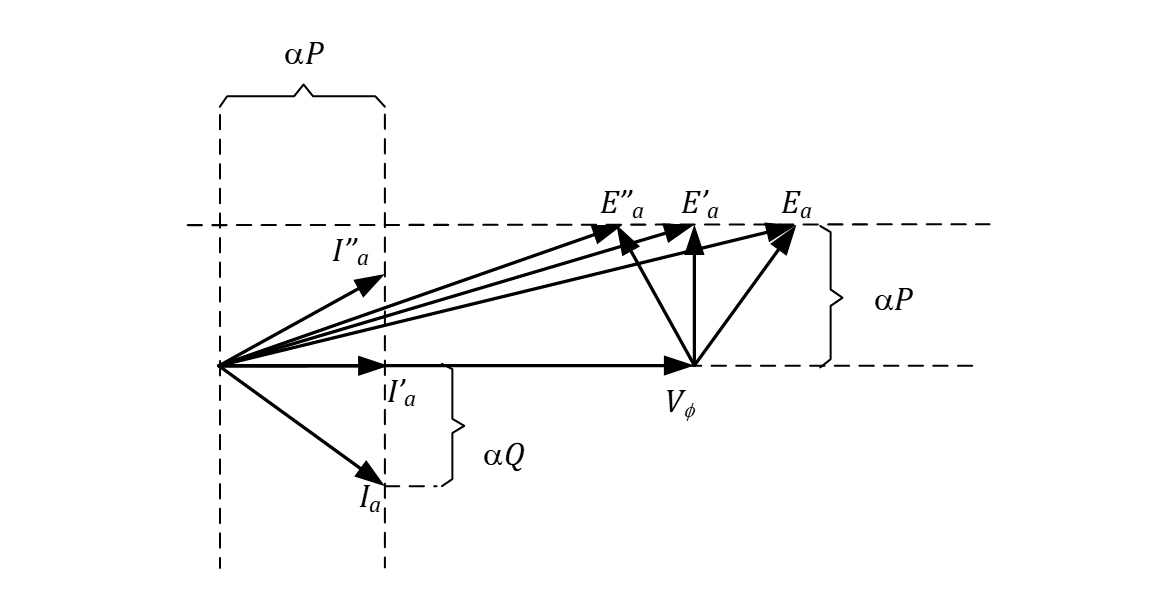
Para fazer com que o gerador forneça reativos para rede, mantendo-se a potência ativa constante, deve-se aumentar a corrente de campo do rotor. O aumento da corrente de campo provocará o aumento da tensão induzida, e a corrente de armadura começará a se atrasar em relação à tensão, conforme a figura abaixo.

Figura 29 – Efeito do aumento da corrente de campo à potência constante.

Valores nominais do gerador

O gerador não pode atender, indiscriminadamente, o aumento de potência ativa ou de potência reativa solicitada pela carga. Para tal, existem limites que devem ser respeitados de modo a não comprometer a vida útil do equipamento e a segurança de seus usuários.

Os valores nominais típicos definidos para o gerador são:

  • Tensão
  • Frequência
  • Velocidade
  • Potência aparente
  • Fator de potência
  • Corrente de campo
  • Fator de serviço

A velocidade nominal da máquina depende do SEP ao qual o gerador está conectado.

Basicamente, existem dois enrolamentos que devem ser protegidos contra superaquecimento, que são:

  • Enrolamento de armadura
  • Enrolamento de campo

A máxima corrente de armadura limita a máxima corrente aparente do gerador, pois:

S = 3 V ϕ I a                     ( 9 - 1 )

A máxima capacidade de condução dos enrolamentos de campo limita a máxima tensão induzida do gerador. Sabemos que a tensão terminal da máquina está associada à potência reativa que ela pode fornecer. No entanto, como determinar o máximo fator de potência com o qual o gerador pode trabalhar?

Considere o diagrama fasorial do gerador indicado abaixo.

Figura 30 – Diagrama fasorial do gerador.

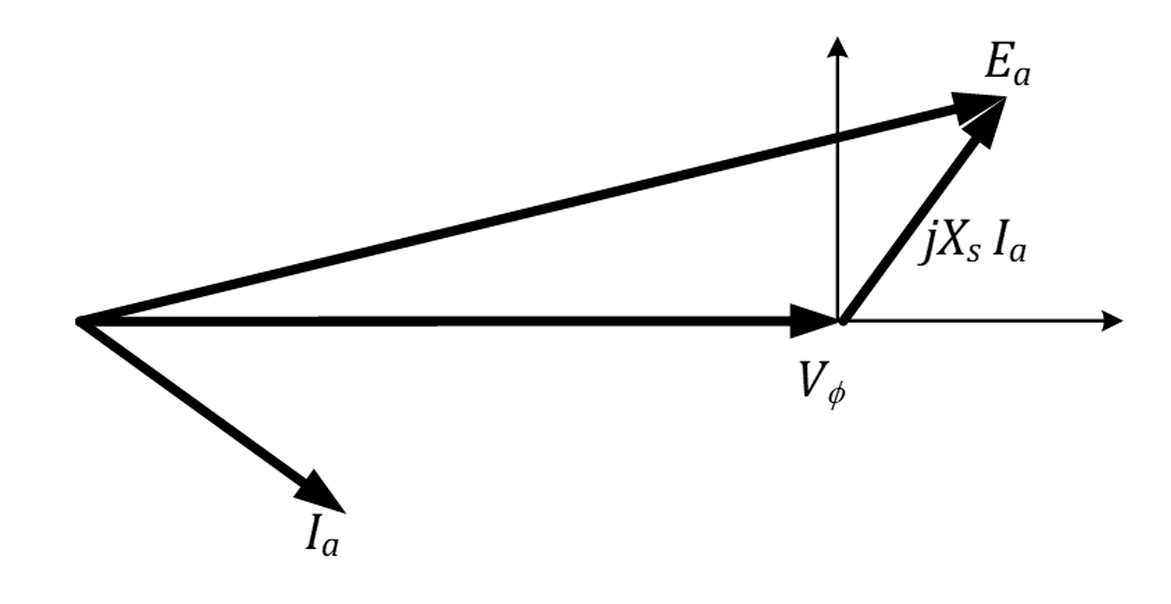
Agora, se cada um dos vetores for multiplicado por 3 V ϕ X s , teremos o diagrama fasorial mostrado na Figura 31

Figura 31 – Diagrama fasorial do gerador multiplicado por 3 V ϕ X s .

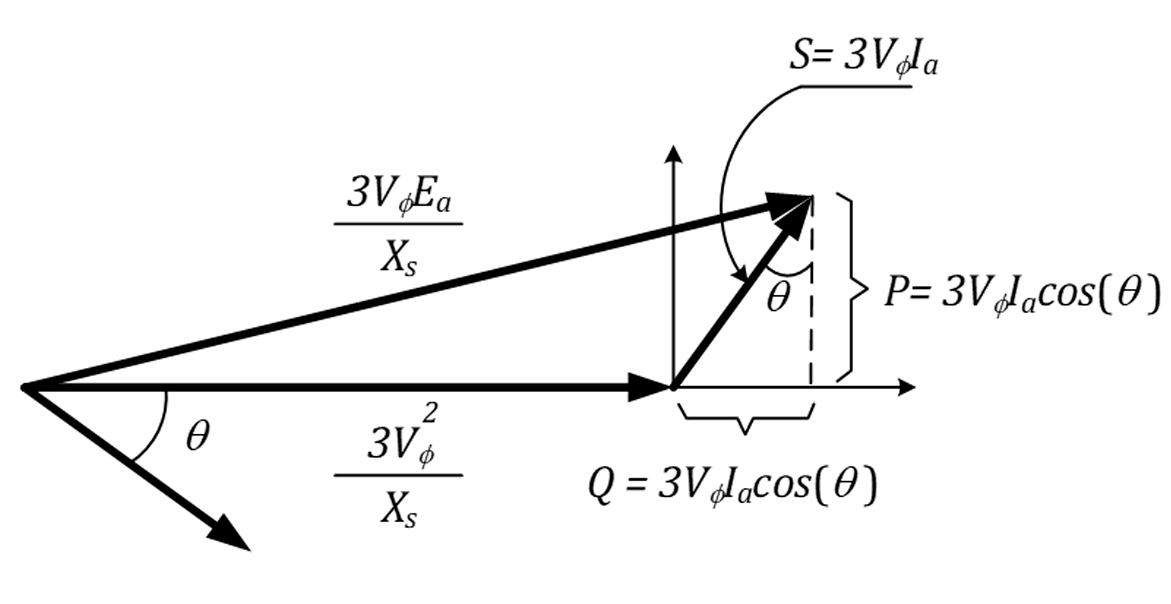
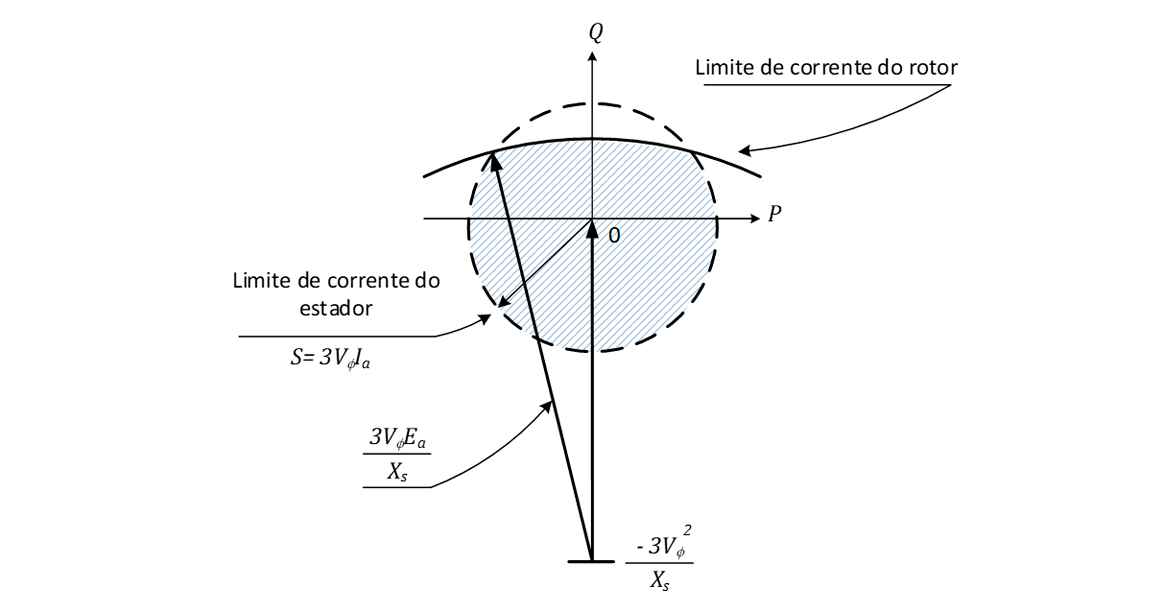
Com as informações do diagrama fasorial da figura anterior, montamos a curva apresentada na Figura 32, conhecida como curva de capacidade da máquina AC. A circunferência tracejada, com centro em 0, indica o limite máximo da corrente de armadura. O arco com centro em - 3 V ϕ 2 X s e com raio 3 E a V ϕ X s indica o limite de corrente do rotor. O ponto de operação da máquina, onde ela não ultrapassa os limites de corrente de campo do rotor e do estator, está identificado pela região hachurada da figura.

Figura 32 – Curva de capacidade da máquina AC.
icone mão na massa

Mão na Massa

icone teoria na prática

Teoria na prática

Um gerador síncrono de 380 V, 60 Hz, conectado em Y, 6 polos, tem seus valores nominais especificados em 60 kVA com um fator de potência de 0,75. Esse gerador possui uma reatância síncrona de 1 Ω por fase. Diante do exposto, desenhe a curva de capacidade do gerador.

Clique no botão para ver a resolução. Objeto com interação.

Curva de capacidade do gerador síncrono.

Assista ao vídeo para conferir a resolução da questão.

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 2

Descrever o funcionamento do motor síncrono sob diferentes condições de operação

Introdução

De acordo com o mencionado, os motores e geradores são a mesma máquina. A diferença entre elas reside no fluxo de potência da máquina. Nos motores, a energia elétrica fornecida aos terminais da máquina é convertida em energia mecânica, que será empregada para realizar trabalho.

Relembrando

Vimos, no módulo anterior, que o campo do rotor girando no interior do estator induzirá tensões alternadas nos enrolamentos de cada uma das fases e que, em função das características construtivas do rotor, essas tensões terão um desfasamento de 120° entre si.

Qual é o comportamento da máquina quando uma tensão alternada trifásica é aplicada em seus terminais?

Veremos isso a seguir.

Princípio de funcionamento

Consoante ao que foi visto no Item Campos magnéticos girantes do módulo anterior, se uma tensão alternada trifásica for aplicada aos terminais do motor, cada uma das correntes de fase criará um campo defasado de 90° das correntes. O campo resultante será um campo magnético girante, que girará na mesma frequência da tensão de alimentação, conforme mostrado na Figura 4.

Considere agora que o campo do rotor seja ligado e posto em movimento devido à aplicação de uma força externa.

força externa

O motor síncrono não consegue dar partida sem um mecanismo auxiliar. Os métodos de partida do motor serão apresentados nas próximas seções.

Um torque induzido, dado pela expressão abaixo, tentará alinhar o campo do rotor com o campo do estator.

τ ind = kB R   ×   B S                     ( 2 - 1 )

A configuração do sistema é apresentada na Figura 34.

Figura 34 – Campos no interior do motor.

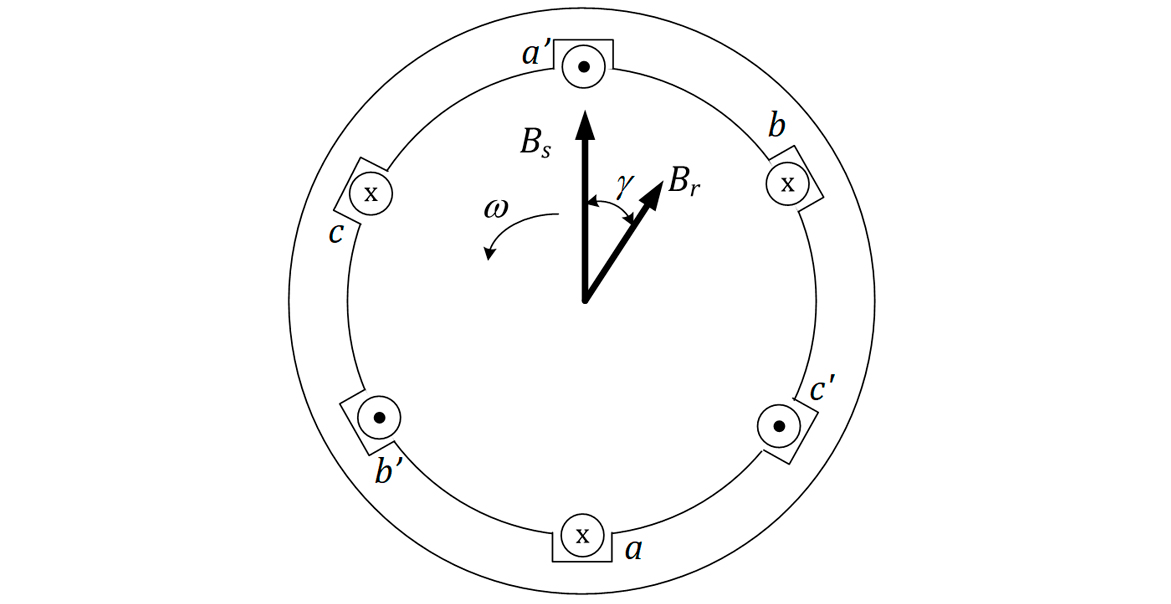
Resumindo

Verificamos que, pela expressão do torque induzido, quanto maior o ângulo, maior será o torque do motor.

Considere que um motor síncrono, girando na velocidade síncrona, acione uma carga.

Qualitativamente, o que acontecerá com o motor quando há um aumento da carga?

Resposta

Resposta

Na ocorrência do aumento de carga, o rotor diminuirá a velocidade e o ângulo de defasagem entre o campo do estator e do rotor (γ) aumentará, o que produzirá um aumento do torque induzido, pois:

τ ind = kB R B S sen ( γ )                     ( 2 - 2 )

Observe que, pela expressão, o torque induzido no motor está no mesmo sentido de giro do rotor.

Esse aumento do torque aumentará a velocidade do rotor até que ele volte à velocidade síncrona. No entanto, os campos estarão com uma defasagem maior do que o original, de acordo com a figura abaixo.

Figura 35 – Aumento da defasagem dos campos em função do aumento de carga.

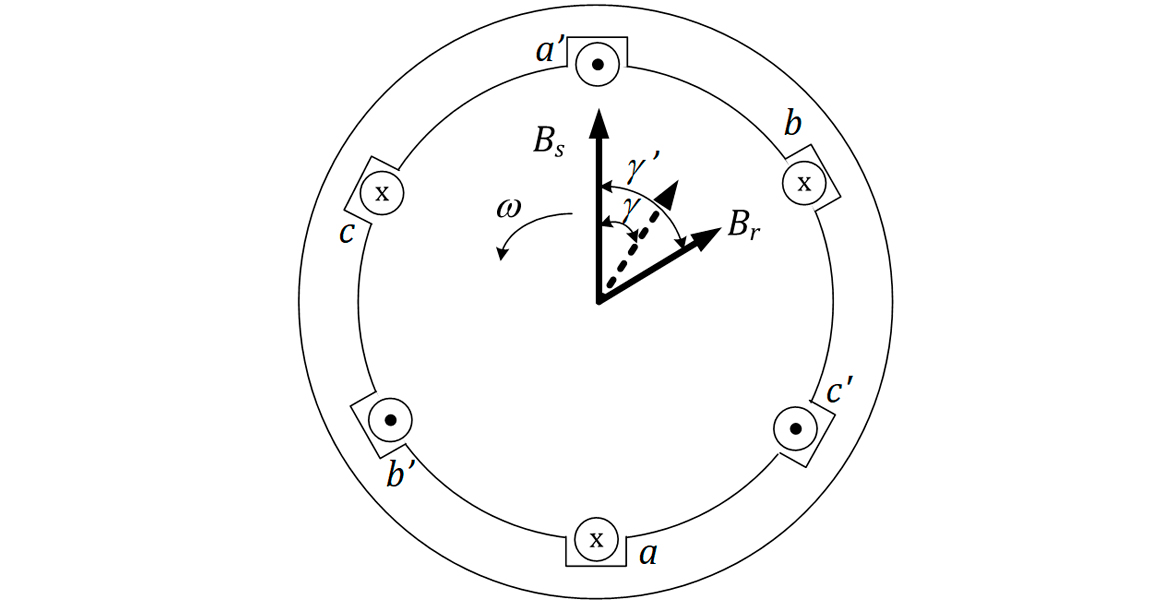
No entanto, essa capacidade de o motor atender o aumento de carga não é infinita. Suponha que o ângulo de defasagem entre os campos seja 90° e que haja um aumento de carga. Nesse instante, a velocidade do rotor diminuirá, aumentando o ângulo de defasagem para mais de 90° e, como sen(90° + Δ) < sen(90°), o torque induzido diminuirá ao invés de aumentar. Com um torque menor, a velocidade do rotor diminuirá ainda mais, fazendo com o que motor perca o sincronismo.

Comentário

Nessa situação, o motor deverá ser retirado de funcionamento.

Por serem a mesma máquina, o gerador síncrono e o motor síncrono apresentam os mesmos circuitos e as mesmas equações. Contudo, o fluxo da corrente é contrário àquele apresentado no gerador, conforme mostra o circuito equivalente monofásico da Figura 36.

Figura 36 – Circuito equivalente monofásico do motor síncrono. | Fonte: autor

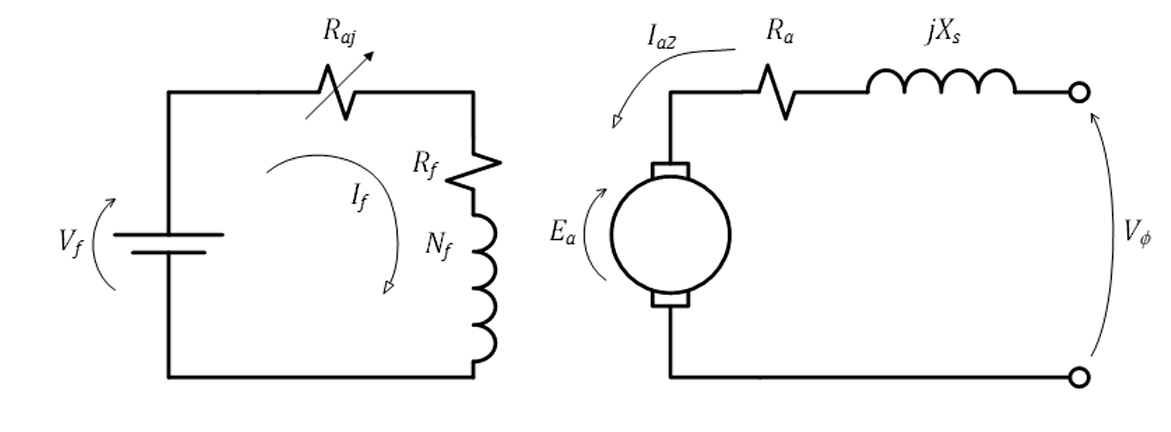
Por esse motivo, as equações do motor síncrono são:

V ϕ = E a + jX s I a + R a I a                     ( 2 - 3 )

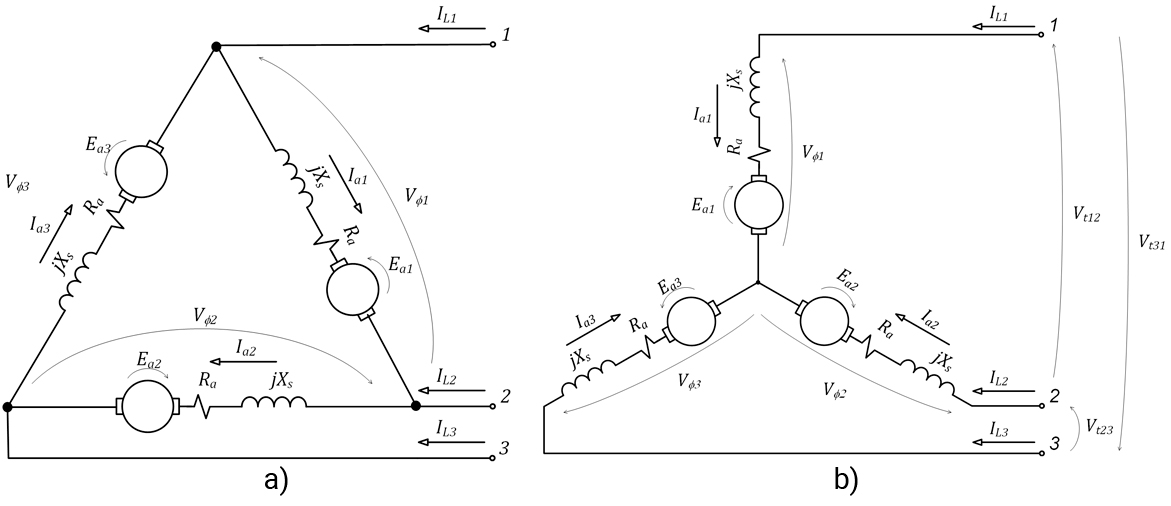
E, da mesma forma que os geradores síncronos, os motores síncronos podem ser ligados em Δ ou Y, conforme apresenta as Figuras 37a e 37b.

Figura 37 – Ligação Δ e Y do motor síncrono.

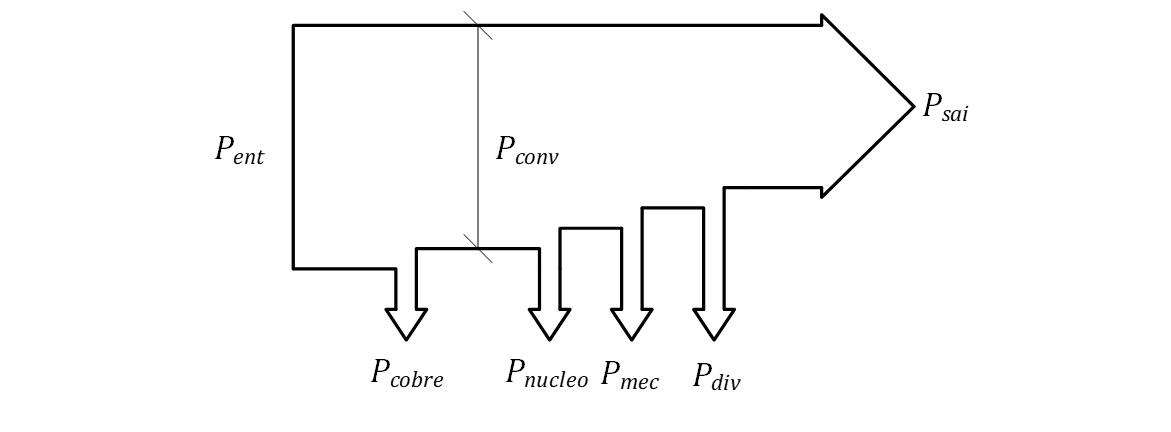
A ilustração, a seguir, mostra o fluxo de potência do motor. Nessa máquina, a potência elétrica de entrada é dada por:

P ent = 3 V ϕ I a cos ( θ ) = 3 V L I L cos ( θ )                     ( 2 - 4 )

Abatidas as perdas no cobre, que valem:

P cobre = 3 R s I A 2                     ( 2 - 5 )

Abatidas as perdas no cobre, temos a potência convertida, que é dada por:

P conv = τ ind ω m                     ( 2 - 6 )

E, abatidas as perdas do núcleo, mecânicas e diversas, chegamos à potência mecânica de saída, que é dada por:

P sai = τ carga ω m                     ( 2 - 7 )

Figura 38 – Fluxo de potência do motor.

Nas duas configurações, o rendimento da máquina será:

η=P_saiPent×100%          (2-8)

Algumas considerações sobre o fluxo de potência:

Não é possível separar as perdas mecânicas e do núcleo. Essas perdas são levantadas em conjunto por meio do ensaio em vazio das máquinas.

As perdas do núcleo são provenientes das perdas por histerese e por correntes parasitas.

Motor sob condições de carga variável

Para analisar o comportamento do motor sob variação de carga, vamos considerar que ele esteja ligado a um barramento infinito, ou seja, possui frequência e tensão terminal constantes, que sua corrente de campo permaneça constante durante a variação da carga e que a sua resistência de armadura seja desprezível em relação à reatância síncrona.

Partindo dessas considerações, suponha que o motor acione uma carga capacitiva e que ele tenha sido submetido a um aumento de carga.

Esse aumento de corrente de carga fará com que a corrente de armadura aumente, aumentando a queda de tensão na reatância de armadura.

No entanto, como a tensão induzida e a tensão de fase são constantes, a corrente deverá se tornar mais indutiva à medida que ela aumenta, conforme a Figura 39 apresenta.

Figura 39 – Aumento de carga do motor.

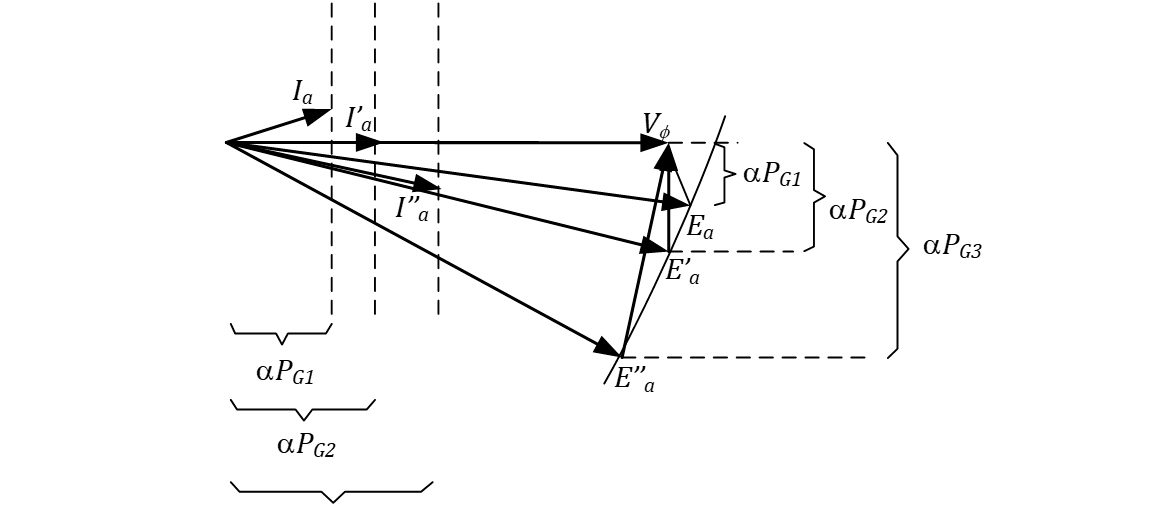
Agora, qual o efeito da variação da corrente de campo do rotor? Como a potência ativa solicitada pela carga é constante, a projeção da tensão induzida no eixo y e a projeção da corrente no eixo x deverão permanecer constantes. Diminuindo-se a corrente de campo, a tensão induzida diminuirá e a corrente ficará mais indutiva, segundo a figura a seguir.

Figura 40 – Aumento da corrente de campo do rotor.

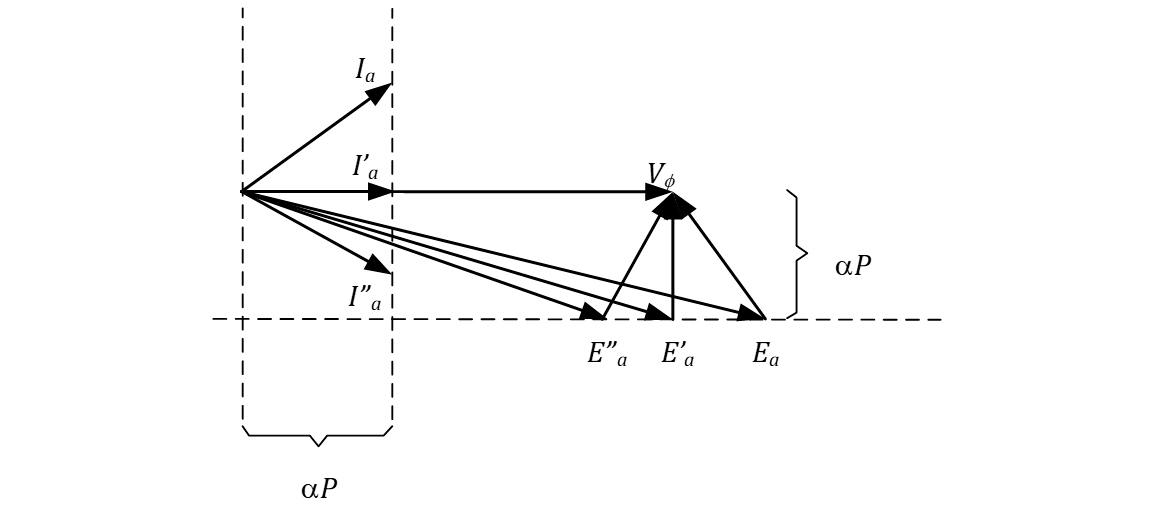
Grandes valores

Para grandes valores de corrente de campo, temos valores maiores de tensão induzida, e a corrente do motor é capacitiva. Nessa condição de operação, dizemos que o motor está superexcitado.

Pequenos valores

Para pequenos valores de corrente de campo, temos valores menores de tensão induzida, e a corrente do motor é indutiva. Nessa condição de operação, dizemos que o motor está subexcitado.

Resumindo

Para dada potência mecânica de saída e o devido ajuste da corrente de campo, o motor pode operar como uma carga indutiva, resistiva ou capacitiva.

Esse comportamento é exibido pela Curva V, da Figura 41.

Figura 41 – Curva V do motor.

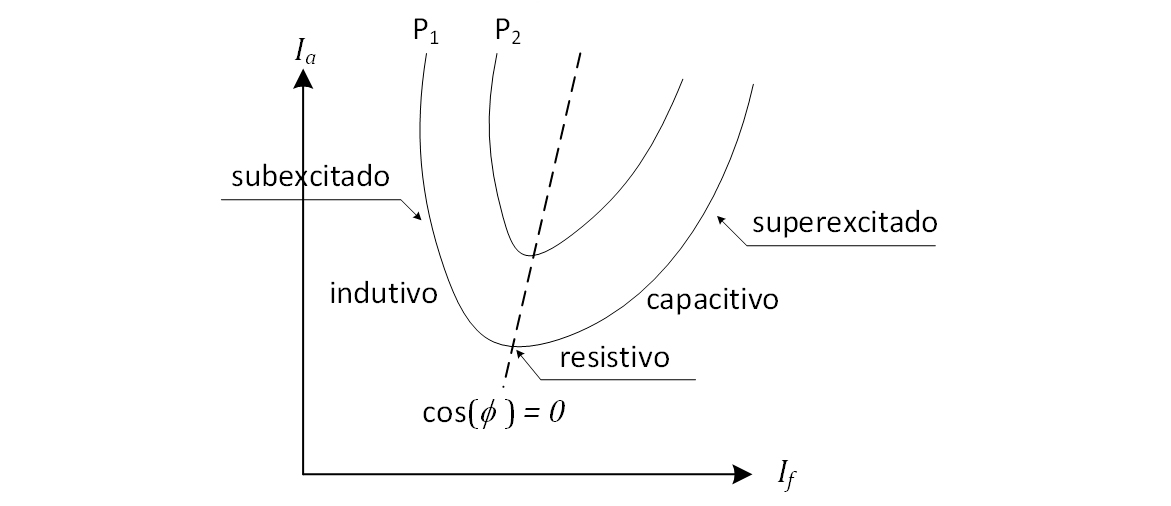
Essa capacidade de o motor operar como um indutor, resistor ou capacitor, mediante o devido ajuste de sua corrente de campo, é bastante importante porque, além de ser capaz de fornecer potência mecânica para suprir uma carga, o motor de indução, operando na região superexcitado, pode ser usado para a correção do fator de potência de uma instalação.

Partida do motor síncrono

Dissemos que o motor síncrono não é capaz de partir sem mecanismo auxiliar. Por que isso ocorre?

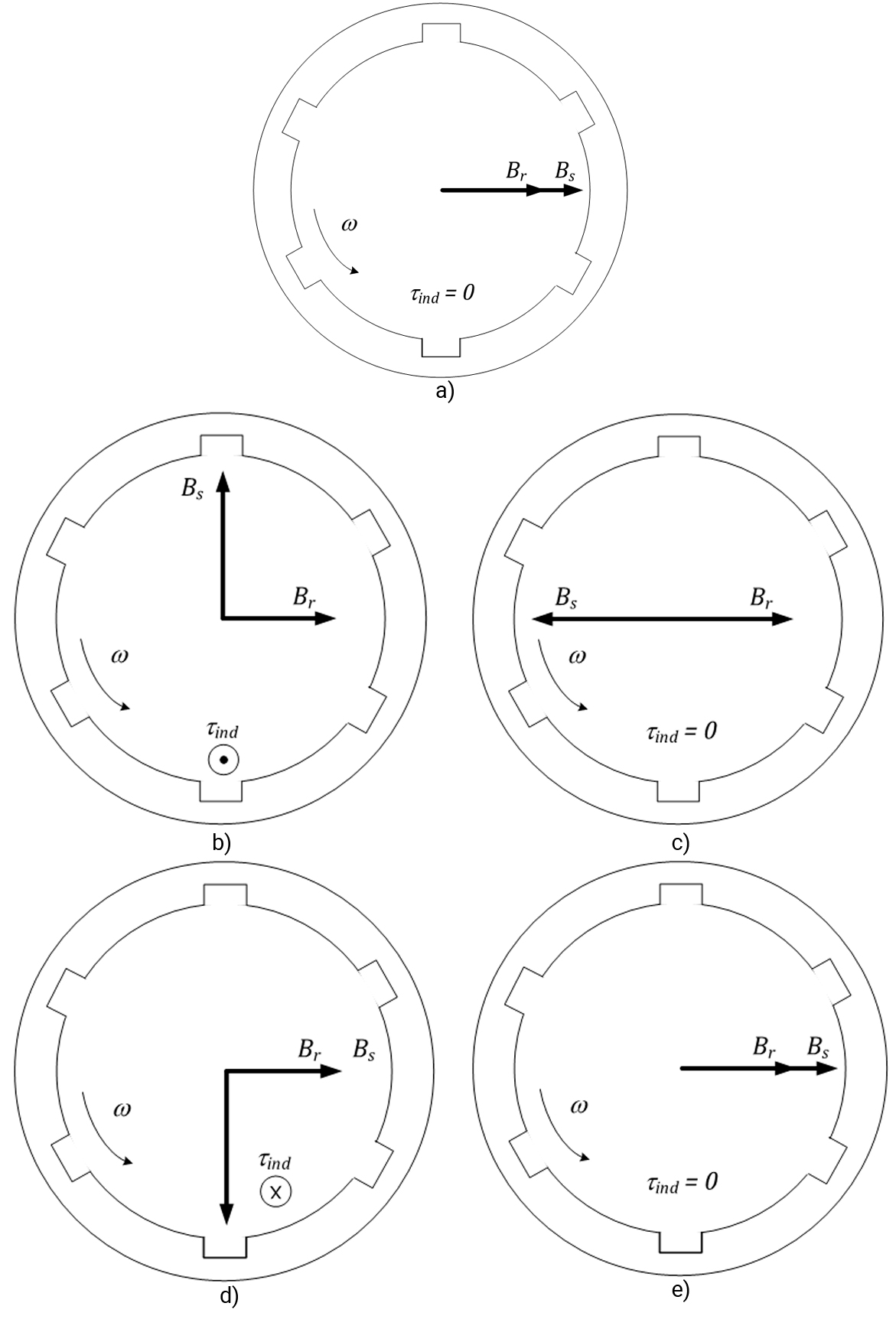
Considere que, no instante t = 0, o motor seja ligado, nesse mesmo instante, gera-se o campo do estator com a velocidade da rede, enquanto o campo do rotor, que estava em repouso, tentará se alinhar ao campo do estator. Suponha que, no instante em que o motor é ligado, os campos do estator e do rotor estejam alinhados, conforme a Figura 42a. Como os campos estão alinhados, o torque induzido será zero. Passado um intervalo de tempo suficiente, o campo do estator se encontrará na posição indicada na Figura 42b e o rotor não terá tido tempo para se rotacionar.

Atenção

Nessa nova posição, o torque induzido apontará para fora do plano da página, fazendo com que o motor gire no anti-horário.

Agora, na posição indicada na Figura 42c, o torque novamente será zero. Na posição indicada na Figura 42d, o torque induzido apontará para dentro do plano da página, fazendo com que o motor gire no sentido horário. E, finalmente, na posição indicada na Figura 42e, o torque induzido será zero.

Podemos concluir que, ao longo de um ciclo do campo do estator, o torque líquido foi zero, ou seja, o rotor não sairá da condição inicial e, consequentemente, a tensão induzida será zero. Isso fará com que a corrente no estator seja elevada, podendo danificar os seus enrolamentos.

As constantes inversões do sentido do torque provocarão a vibração do motor.

Figura 42 – Torque induzido no rotor ao longo de um ciclo do campo do estator.

Como fazer para contornar esse problema?

Para permitir a partida do motor, podemos adotar os seguintes procedimentos:

Clique nas barras para ver as informações. Objeto com interação.
Redução da velocidade do campo do estator

A redução da velocidade do campo é alcançada mediante a redução da frequência da tensão aplicada aos terminais do motor. Com o campo do estator rotacionando em baixa velocidade, o rotor terá condições de se alinhar com o campo do estator. A partir de determinado ponto, a frequência da tensão de alimentação passa a ser a frequência nominal e o motor entrará em sincronismo com a rede.

 Fonte de energia externa para dar partida no motor

Uma fonte mecânica externa dará a velocidade inicial ao rotor do motor. Em seguida, aplica-se tensão nos terminais do motor. Por ter um movimento inicial, o campo do rotor terá condições de se alinhar ao campo do estator.

Usar o enrolamento amortecedor

Os enrolamentos amortecedores são barras posicionadas nas ranhuras do rotor, curto-circuitadas por um anel.

Considere o corte do enrolamento amortecedor mostrado na Figura 43. Suponha que, no momento indicado na figura, o campo do estator Bs esteja na posição indicada. A projeção do campo do estator no eixo x, Bsx, diminuirá ao longo do tempo, e a projeção do campo do estator no eixo y, Bsy, aumentará ao longo do tempo. Por estar no plano da espira, Bsy não induz tensão no enrolamento amortecedor. Porém, Bsx será variável ao logo de todo o ciclo do campo do estator e induzirá tensão no enrolamento amortecedor.

Na posição indicada na figura, Bsx diminuirá e induzirá uma corrente no enrolamento amortecedor de modo a se contrapor a essa diminuição. Essa corrente produzirá o campo do enrolamento amortecedor, Ba. Então, o campo Ba tentará se alinhar com o campo Bsy, produzindo um torque no rotor no sentido anti-horário.


Figura 43 – Partida com enrolamento amortecedor (Bs no primeiro quadrante).

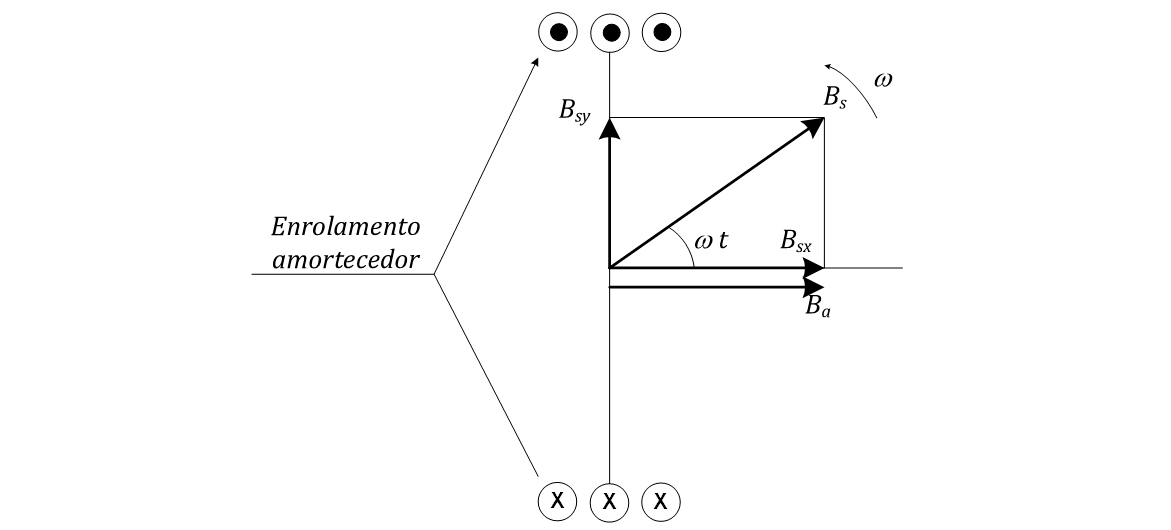
Quando o campo Bs, estiver totalmente contido no eixo y, a tensão induzida no enrolamento amortecedor será zero, não haverá campo Ba e o torque induzido será zero.

Suponha, agora, que Bs, esteja no segundo quadrante, conforme a Figura 44. A projeção de Bsx, aumentará e a corrente induzida no enrolamento amortecedor produzirá um campo Ba no sentido indicado na figura. O campo Ba tentará se alinhar com o campo Bsy, produzindo um torque no rotor, novamente, no sentido anti-horário.

Estendendo esse raciocínio para os demais quadrantes, você concluirá que o torque sempre apontará para o sentido horário ou será zero e, por isso, o motor ganhará velocidade, permitindo a sua partida.

Figura 44 – Partida com enrolamento amortecedor (Bs no segundo quadrante).

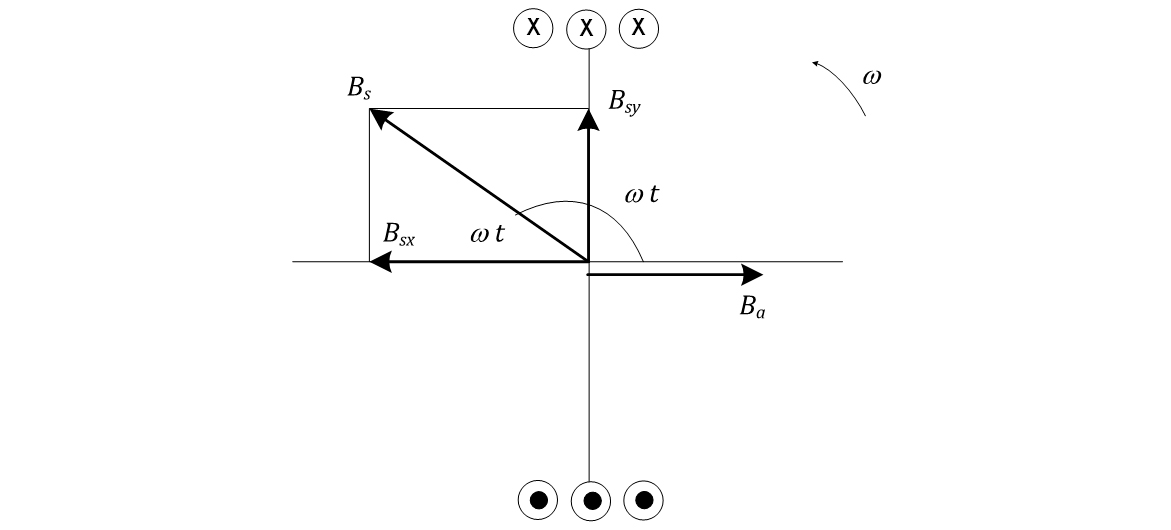
Próximo a atingir sua velocidade nominal, o enrolamento amortecedor deverá ser desconectado para que o motor atinja a velocidade nominal.

Por que devemos desconectar o enrolamento amortecedor para que o motor atinja a velocidade nominal?

Resposta

Resposta

Se o rotor rotacionar com a mesma velocidade do campo do estator, não haverá movimento relativo entre o rotor e o campo do estator. Sem movimento relativo, não haverá variação de fluxo e, consequentemente, a tensão induzida será zero. Dessa forma, a corrente induzida será zero e o campo Bw será zero, e o torque induzido será nulo.
icone mão na massa

Mão na Massa

icone teoria na prática

Teoria na prática

Uma instalação industrial hipotética possui dois motores de indução trifásicos, cujos dados são apresentados a seguir

Motor 1
Potência ativa: 200 kW
Fator de potência: 0,70 (indutivo)

Motor 2
Potência ativa: 300 kW
Fator de potência: 0,75 (indutivo)

Você decide corrigir o fator de potência da fábrica usando motor síncrono como capacitor síncrono. Diante do exposto, para que o fator de potência da instalação seja corrigido 0,92 (ind), qual deve ser a potência reativa do motor, em kVAr?

Clique no botão para ver a resolução. Objeto com interação.

Correção de fator de potência com motor síncrono

Assista ao vídeo para conferir a resolução da questão.

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

Conclusão

Considerações Finais

Ao longo dos módulos, estudamos as máquinas síncronas, partindo do seu princípio de funcionamento, suas características sob diferentes condições de operação até chegar a casos especiais de funcionamento.

Vimos que, fundamentalmente, o gerador síncrono AC e o motor síncrono AC são a mesma máquina. O que as diferencia é o fluxo de energia da máquina. Além disso, observamos as aplicações práticas dos motores síncronos, em especial a sua utilização para a correção de fator de potência.

Por fim, acreditamos que você tenha condições de determinar os parâmetros de funcionamento das máquinas AC, descrever seus princípios de funcionamento e calcular as suas condições de operação em regime permanente.

Podcast

Você atingiu os seguintes objetivos:

Descreveu o funcionamento do gerador síncrono sob diferentes condições de operação

Descreveu o funcionamento do motor síncrono sob diferentes condições de operação

Referências

CHAPMAN, Stephen J. Fundamentos de máquinas elétricas (Minha Biblioteca). 5. ed. Porto ALegre: Bookman, 2013.

UMANS, Stephen D. Máquinas elétricas (Minha Biblioteca). 7. ed. Porto Alegre: AMGH, 2014.

Explore+

Para saber mais sobre os assuntos tratados neste tema, resolva os exercícios constantes nos livros das referências.

Conteudista

Sandro Santos de Lima

Currículo Lattes