Descrição
Conceituação e emprego das estruturas de dados, listas, pilhas e filas empregando a linguagem C.
PROPÓSITO
Compreender as estruturas de dados como as listas e seus casos particulares, pilhas e filas, desenvolve a capacidade de abstração e melhora a compreensão da interligação entre os diversos elementos envolvidos na execução de um programa de computador, facilitando a abordagem de conceitos mais complexos, como árvores e grafos, dando ao profissional ferramentas que ampliam o portfólio de soluções, facilitando o entendimento e a resolução de problemas.
Preparação
Para melhor absorção do conhecimento, recomenda-se o uso de computador com compilador de linguagem C e uma IDE (Integrated Development Environment) instalados.
OBJETIVOS
Módulo 1
Reconhecer os principais conceitos envolvidos na manipulação de dados na memória
Módulo 2
Contrastar a forma de manipulação por encadeamento da manipulação com estruturas sequenciais
Módulo 3
Identificar os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de pilhas
Módulo 4
Reconhecer os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de filas
Introdução
Neste tema, abordaremos os conceitos básicos relacionados às estruturas de dados. Uma estrutura de dado é uma organização coerente de dados e respectivas operações, que permitem uma manipulação eficiente. São, dessa maneira, elementos fundamentais no aprendizado do profissional de TI.
Apresentaremos o assunto com o emprego da linguagem de programação C. Essa abordagem busca concretizar a aplicação dos conceitos aprendidos, evitando-se uma visão apenas teórica.
Mas você não deve entender que o tema seja inerente a uma linguagem específica. As estruturas de dados são, de fato, conceitos teóricos que podem ser implementados por quaisquer linguagens de programação. Observar a forma como esses conceitos são construídos numa linguagem ajudará a compreender nuances do seu funcionamento.
A sequência de apresentação inicia-se com a abordagem de conceitos genéricos de manipulação de memória. Em seguida, definiremos a estrutura de dados genérica chamada lista. As pilhas e as filas, apresentadas posteriormente, nada mais são do que casos particulares que, por sua relevância, são estudados em maior profundidade.
Todos esses conceitos são colocados juntos, criando uma visão abrangente e fundamentando conceitos mais avançados.
MÓDULO 1
Reconhecer os principais conceitos envolvidos na manipulação de dados na memória
Nesta seção, entenderemos o que são listas e como estas são implementadas através de um mecanismo chamado alocação sequencial. Veremos, então, o que é a alocação sequencial e, posteriormente, como esse mecanismo viabiliza o emprego das listas e como se dão as principais operações. Abordaremos, ainda, alguns casos particulares de listas, mas deixaremos outros, mais relevantes, para análise em outros módulos.
Entendendo a alocação sequencial
O primeiro conceito que você precisa ter bem claro é o de alocação sequencial. Esse tipo de alocação, como o próprio nome já revela, é o armazenamento de dados de forma sequencial na memória do computador. Isto quer dizer que as posições de memória ocupadas serão contíguas.
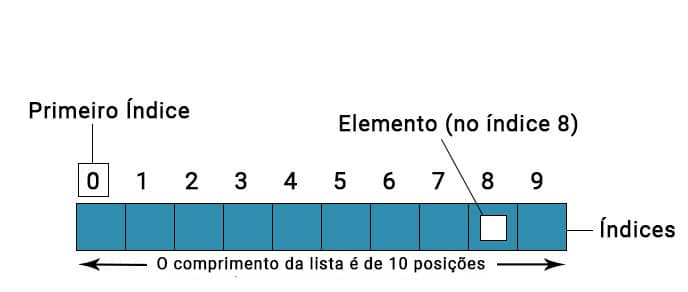
Numa situação real, a memória do computador é ocupada por diversos outros dados que são armazenados pela execução de outros programas, deixando espaços de tamanhos diversos desocupados.
Para que a alocação sequencial possa ser levada a termo, o programa precisa informar previamente todo o tamanho de memória que será necessário. Há duas estratégias, como veremos mais à frente, mas ambas envolvem a alocação de toda a memória necessária, diferindo apenas se esse valor é determinado em tempo de compilação ou de execução.
Saiba mais
Em linguagens de programação de alto nível, a alocação sequencial é representada pelos arrays ou vetores.
Um vetor indica ao compilador que este deve solicitar a reserva de um número de posições de memória suficientes para guardar todos os elementos do vetor. Para isso, faz-se necessário especificar o tipo de dado que será armazenado. Vamos observar o exemplo a seguir, que é um trecho de código em linguagem C no qual um vetor é declarado.
Código 1: Alocação sequencial na linguagem C.
[...]2:
int vetor [ 10 ];3:
int a = 50;4:
vetor [ 3 ] = a;5:
[...]A linha 2 desse código informa ao compilador que deverão ser reservadas posições de memória suficientes para armazenar 10 elementos do tipo inteiro. Você deve ter reparado que estamos falando em posição de memória, e não em tamanho. A razão disso é que o número de posições necessárias depende do tamanho do tipo de dado e da palavra da memória.
Exemplo
Por exemplo, considere que o tipo de dados “int” em C tenha o tamanho mínimo definido na especificação C99 (16 bits). Suponha, a título de exemplo, uma memória cuja palavra seja de 8 bits. Logo, cada posição de memória pode armazenar 1 byte (8 bits). Assim, para armazenar 10 elementos do tipo inteiro serão necessárias 10 * (16 / 8) = 20 posições de memória. Observe que cada elemento ocupará duas posições de memória.
(ISO, 2011)
Voltando ao Código 1, agora compreendemos como o compilador, de posse dos parâmetros necessários, gera o código que instrui o sistema operacional a alocar o espaço sequencial para armazenar o vetor.
Mas isso não é tudo. Sabemos também que os elementos de um vetor podem ser acessados diretamente através do seu índice. Isso é possível porque na verdade o índice corresponde ao offset ou deslocamento a ser feito a partir do endereço do primeiro elemento do vetor.
Nesse caso, a linha 4 do exemplo está acumulando o valor de “a” no quarto elemento do vetor (em C, o vetor inicia com índice zero). Isso quer dizer saltar 6 posições de memória (3 (índice do vetor) * 2 (número de posições de memória que cada elemento ocupa) = 6).
Uma maneira de se criar uma lista em memória é através da alocação sequencial. Como nesse caso todos os seus nós estarão em posições contíguas, isso tem vantagens para o acesso.
Em contrapartida, operações como a remoção são prejudicadas, pois não é possível desalocar o espaço de memória sem comprometer a sequencialidade das posições. Esse tipo de operação é mais bem suportada pela alocação dinâmica.
Portanto, a escolha da melhor forma de implementação da lista dependerá de uma análise das vantagens e desvantagens.
Compreender o que é alocação sequencial vai lhe ajudar não apenas no entendimento de como estruturas tais quais listas, filas e pilhas funcionam, mas também na compreensão do mecanismo da alocação dinâmica.
Conceitos e operações em listas lineares genéricas
Consideraremos, para fins didáticos, que as listas lineares estão implementadas através de alocação sequencial em vetores de tamanho ilimitado. Posteriormente, quando aprofundarmos o estudo, trataremos os casos reais de listas alocadas sequencialmente.
Listas lineares são estruturas de dados não primitivas, usadas para reunir um conjunto de elementos que guardam relação entre si.
Listas lineares
Formalmente, segundo Szwarcfiter e Markenzon (2010), uma lista linear é um conjunto de n ≥ 0 nós, tais que suas propriedades estruturais decorrem, unicamente, da posição relativa dos nós dentro da sequência linear. Ou seja, se n = 0, a lista é vazia; se n > 0, então qualquer que seja k, tal que 1 < k ≤ n, o nó L[k] é precedido pelo nó L[k-1], exceto para o nó L[1], que é o primeiro nó da lista.
Uma lista linear pode armazenar tipos de dados complexos, isto é, cada nó pode ter campos que armazenam elementos com características distintas. Pode-se designar um desses campos como sendo a chave de busca da lista, o qual é utilizado para indexar os nós e é chamado de “chave”.
Saiba mais
Quando a lista apresenta seus nós ordenados segundo a “chave”, essa lista é chamada de ordenada. Caso contrário, trata-se de uma lista não ordenada. Observe que, para que seja uma chave de busca, a “chave” deve ser única (todos os campos “chave” devem ser distintos entre si e correlacionados com o mesmo elemento).
As listas apresentam casos particulares, chamados de deque, pilha e fila. Tais casos se diferenciam pela forma como as operações de inserção e remoção podem ocorrer na lista. Mas antes de estudarmos esses casos, vamos compreender o funcionamento das operações de inserção, remoção e busca para o caso geral.
Observe os pseudocódigos a seguir, nos quais a lista é representada por “Lista” e possui “n” posições ocupadas.
Algoritmo 1: Busca
1: int buscar ( chave )
2: se n > 0
3: para i = 1 até i <= n
4: se Lista [ i ].chave == chave
6: retornar i
7: retornar n + 1
Repare que no caso da busca (Algoritmo 1) de um elemento da lista, esta é percorrida a partir do início até que o elemento seja encontrado ou o fim da lista seja atingido. O pior caso da busca se dá quando o elemento ocupa a última posição da lista ou não está na lista, o que obriga a se percorrer toda a lista.
Algoritmo 2: Inserção
1: int inserir ( novo_elemento )
2: se busca ( novo_elemento.chave ) == n + 1
3: Lista [ n + 1 ] == novo_elemento
4: n = n + 1
5: retornar 1
6: senão retornar -1
A inserção (Algoritmo 2) precisa, antes de mais nada, verificar se o elemento a ser inserido já se encontra na lista (lembre-se de que as chaves são únicas e distintas). Nesse caso, se o valor retornado da busca for maior que o número de elementos (n) da lista, isso quer dizer que o novo elemento pode ser inserido. Como não se trata de uma lista ordenada, o novo elemento será inserido após a última posição ocupada. Note que se trata de um caso simples, uma vez que a não ocorrência do elemento permite sempre o inserir após a última posição ocupada.
Algoritmo 3: Remoção
1: int remover ( chave )
2: se n > 0
3: int i = busca ( chave )
4: se i < n + 1
5: para a = i até a < n
6: Lista [ i ] = Lista [ i + 1 ]
7: n = n -1
8: senão retornar -1
9: senão retornar “Erro: lista vazia”
O algoritmo de remoção (Algoritmo 3) também precisa realizar a busca inicialmente, uma vez que remover um elemento inexistente irá gerar erro. Se esse elemento for encontrado, basta sobrescrever a sua posição com o elemento da posição seguinte e, assim, sucessivamente, até o fim da lista. Talvez lhe pareça um pouco mais difícil apontar a complexidade de pior caso, mas isso é apenas aparente. Na verdade, se você considerar que, seja qual for a posição do elemento a ser removido, todos os elementos posteriores serão manipulados, você perceberá que esse algoritmo sempre opera sobre todos os elementos da lista: Até encontrar, compara; depois de encontrado, copia.
Comentário
Convém lembrar que, na prática, há outros detalhes que devem ser considerados. Nos casos anteriores, consideramos que nosso vetor não tinha limite. Essa é uma suposição teórica. Na realidade, o espaço em memória é limitado.
Quando o espaço necessário para guardar os vetores é alocado antecipadamente (o cálculo prévio da quantidade de memória é trivial, como vimos), a alocação é chamada estática. Nesse caso, a quantidade de memória não pode ser alterada em tempo de execução. Isso explica, por exemplo, porque nosso Algoritmo 3 desloca uma posição para a esquerda todos os elementos à direita do que foi removido, ao invés de simplesmente desalocar o elemento a ser removido.
Além disso, na prática, a inserção precisaria verificar se o tamanho do vetor seria ultrapassado com a inserção de um elemento, o que geraria um erro de “overflow”.
Contudo, é possível realizar alocação sequencial de memória com o tamanho definido em tempo de execução. Esse tipo de alocação é chamado de dinâmica e faz uso, em linguagem C, de instruções de reserva de memória como a malloc e outras do tipo. Observe o trecho de código a seguir:
Código 2: Alocação dinâmica
[...]1:
int *vetor;2:
vetor = ( int * ) malloc ( tamanho_vetor * sizeof ( int ) );[...]A função malloc solicita ao sistema operacional que reserve, em tempo de execução, uma área contígua de memória igual à “tamanho_vetor” * o tamanho do tipo inteiro.
A variável “tamanho_vetor” pode ser determinada durante a execução do programa.
Como na linguagem C o nome do vetor é um ponteiro para o endereço base desse vetor e os índices são offsets (deslocamentos) a partir desse endereço base, a instrução “vetor [ n ]” tem o mesmo comportamento que no exemplo 1. Isto é, “n” significa o deslocamento a partir do endereço apontado por “vetor”.
Olhemos agora o caso de uma lista ordenada e vejamos qual proveito podemos tirar disso. Obviamente, todos esses algoritmos podem ser aplicados, pois foram pensados para casos gerais. Mas a lista ordenada nos oferece uma vantagem.
Mão na Massa
Considere, por exemplo, a seguinte lista: [1, 3, 6, 7, 9, 12, 15, 22, 90]. Suponha que você esteja buscando o elemento de valor 5. Pois bem, consultando o elemento central da lista (9), verificamos que ele é maior do que o elemento buscado.
Etapa 01
Dessa forma, podemos descartar todos os elementos do meio até o fim (pois como se trata de uma lista ordenada, sabemos que o 5, se existir, estará à esquerda de 9).
Etapa 02
Agora, repitamos o procedimento considerando apenas a primeira metade da lista ( [1, 3, 6, 7, 9] ). Nesse caso, o elemento de valor 6 (central) é maior do que o buscado.
Etapa 03
Portanto, repetimos o procedimento para o primeiro quarto da lista ( [1, 3] ). É fácil ver que após a última repetição ‒ segundo oitavo da lista ( [3] ), teremos como resposta que o elemento buscado não faz parte da mesma.
O procedimento realizado acima, se você observou atentamente, faz chamadas recursivas a si mesmo sempre dividindo ao meio o espaço de busca. Esse procedimento é chamado de busca binária. Ou seja, tiramos proveito do fato de se tratar de uma lista ordenada, para tornar a busca mais eficiente. A função exibida no Código 3 mostra a implementação da busca binária em C.
Código 3: Busca binária
1 int busca_binaria ( int lista [ ] , int elemento , int inicio , int fim ) {
2 int meio = floor ( ( fim + inicio ) / 2 );
3 if ( ( inicio == fim ) && ( lista [ meio ] != elemento ) )
4 return -1;
5 else if ( lista [ meio ] == elemento )
6 return meio;
7 else if ( elemento < lista [ meio ] )
8 busca_binaria ( lista , elemento , inicio , meio );
9 else busca_binaria ( lista , elemento , meio + 1 , fim );
10 }
Olhemos agora mais um caso particular de listas, as chamadas double ended queue ou “deque”. Nessas listas, as inserções e remoções somente são permitidas nas extremidades. Não há um início e um fim propriamente ditos, pois as inserções podem ocorrer antes da extremidade esquerda e/ou após a extremidade direita. Isso vale para a remoção.
Em outras palavras, a lista deque pode crescer pela esquerda, pela direita ou por ambas as extremidades (o encurtamento, é análogo). Isso tem algumas implicações para nossos algoritmos. A inserção e a remoção somente podem ser realizadas em pontos determinados (extremidades), e o acesso à memória é direto, pois trata-se de alocação sequencial.
Vimos anteriormente que na alocação sequencial não temos como desalocar o espaço de memória do elemento removido. A solução para isso seria mover todos os elementos à sua direita de forma a sobrescrevê-lo e registrar o encurtamento da lista. Mas isso é um caso geral que comporta remoções internas. Na verdade, se limitamos a remoção às extremidades, esse problema se torna consideravelmente mais simples.
Considere o vetor v = [ a, b, r, t, c, p]. Trata-se claramente de uma lista não ordenada com 6 elementos. Sendo “v” um deque, os únicos elementos que podem ser removidos são o “a” e o “p”.
Vamos usar duas variáveis auxiliares, “aux_esq” e “aux_dir” que registram as posições extremas ocupadas, respectivamente, à esquerda e à direita. No caso, aux_esq = 0 e aux_dir = 5. Para remover “a”, tudo que precisamos fazer é incrementar aux_esq, que passará a valer 1. Dessa forma, a posição 0 é considerada disponível.
Mas essa limitação não é o único problema. Voltemos ao nosso exemplo. Suponha que tenham sido removidos “a” e “b” e se deseje inserir “u” à direita. Essa inserção viola o limite do vetor, gerando overflow, mas na verdade há espaço disponível para tal inserção.
O problema é que como esse espaço está antes da extremidade esquerda, ele não pode ser utilizado, o que acaba desperdiçando memória. Uma forma elegante de se contornar essa limitação é utilizar-se uma lista circular.
Uma lista circular é uma lista na qual as extremidades direita e esquerda estão ligadas. Assim, ultrapassar o limite superior direito, leva à extremidade esquerda, enquanto ultrapassar o limite inferior esquerdo, leva à extremidade direita.
Colocando de outra forma, ao movermo-nos para a esquerda em nosso vetor exemplo “v”, antes da posição 0, estaria a posição 5. Ao movermo-nos para a direita, após a posição 5, está a posição 0. É óbvio que esse não é o comportamento de um vetor, mas tal comportamento pode ser codificado nos algoritmos de remoção e inserção, de forma que a lista se comporte como a lista circular teórica.
Comentário
Não podemos nos esquecer, contudo, que novos testes de controle precisam ser feitos, de forma que se evite, por exemplo, que uma inserção sobrescreva inadvertidamente um elemento não removido.
Você também não deve confundir esse artifício, que visa ao uso eficiente de memória, com o aumento da capacidade de um vetor. Usemos listas circulares ou não, o número máximo de elementos que um vetor comporta é igual ao número de posições contíguas de memória alocadas.
Como dissemos anteriormente, o uso de alocação sequencial é uma forma de se implementar listas. Conforme mostramos, há vantagens e desvantagens que devem ser pesadas antes da decisão de qual mecanismo utilizar. Na seção seguinte, compreenderemos outro mecanismo de alocação, chamado de alocação encadeada.
APLICANDO LISTAS SEQUENCIAIS
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Contrastar a forma de manipulação por encadeamento da manipulação com estruturas sequenciais
Listas lineares dinamicamente encadeadas
Para compreendermos as vantagens de se utilizar a alocação encadeada, convém primeiramente olharmos mais detidamente para a manipulação de memória em um computador.
Ao longo do tempo, devido à execução de múltiplos programas, alocações e desalocações de memória vão deixando espaços com tamanhos distintos disponíveis. Esse problema é chamado de fragmentação de memória e vai tornando cada vez mais difícil alocar posições contíguas de memória na heap.
Comentário
O impacto mais claro da fragmentação de memória é no desempenho.

Teoria na prática
Olhemos um caso exemplar simples. Um programa que começou a ser executado solicita um espaço de memória para alocar um vetor de inteiros. O problema a ser resolvido pelo sistema operacional não é apenas reservar um espaço. Ele primeiro precisará varrer a sua tabela de alocação buscando um espaço de memória suficientemente grande para caber o vetor.
A situação ideal, porém, é alocar o vetor num espaço disponível idêntico ao necessário, pois isso minimiza as chances de que o espaço excedente nunca seja utilizado, sendo desperdiçado.
Para isso, não é suficiente ele reservar o primeiro espaço disponível, ele precisará verificar se existe em toda a tabela um espaço de tamanho idêntico ao necessário. Essa situação ilustra bem uma das formas como a fragmentação impacta a performance.
A alocação encadeada é uma forma de se contornar esse problema, reduzindo a sobrecarga com o gerenciamento de memória. Dessa forma, como veremos na próxima subseção, os espaços de memória alocados não precisam ser do tamanho da lista, mas apenas do tamanho do elemento da lista, sendo suficiente que se guarde, de alguma forma, a relação entre eles. A última subseção explorará a implementação de lista e suas operações através desse mecanismo.
Entendendo a alocação encadeada
No caso da alocação sequencial, a relação entre os elementos da lista é trivialmente construída. Para que o “i-ésimo” elemento seja posterior ao “(i-1)-ésimo” elemento, basta que eles sejam inseridos, respectivamente, nas posições “i” e “i-1” do vetor. Entretanto, como veremos, o mesmo não se dá na alocação encadeada.
Comentário
A primeira coisa que precisamos ter em mente é que o conceito de lista visto na seção anterior continua válido. O que muda é apenas o mecanismo usado para implementar uma lista.
A ideia por trás da alocação encadeada é simplesmente alocar os espaços de memória suficientes para guardar os elementos individualmente e encadeá-los de forma a manter a relação entre eles.
Assim, cada elemento da lista ocupará uma posição de memória que pode ou não ser adjacente às demais.
É claro que isso traz um problema óbvio: Como acessar os elementos da lista?
Revendo a alocação sequencial, lembramos que todos os elementos eram acessíveis por ser o índice do vetor um deslocamento a partir do endereço base do mesmo, endereço esse que era conhecido. Logo, através de cálculos simples, todas as posições de memória podiam ser acessadas.
Esse, contudo, não, é o caso aqui. Os elementos na alocação encadeada estão armazenados em posições quaisquer da memória. Logo, não há uma forma de se calcular o endereço dessas posições. A solução para esse problema, todavia, é simples. Basta que em cada elemento, adicionemos um campo (ponteiro) responsável por guardar o endereço de memória do elemento seguinte.
Na alocação encadeada, cada elemento é chamado de nó.
Vamos criar um nó especial, chamado “nó cabeça”, cuja finalidade é apenas simplificar as operações sobre a lista. A criação desse nó não é obrigatória, mas usá-lo evitará uma série de testes lógicos que precisaríamos fazer.
O endereço para o nó cabeça precisa ser conhecido sempre.
Assim, precisaremos, de um ponteiro que guarde o seu endereço. Quando a lista for vazia, existirá apenas o nó cabeça e o seu campo “prox” terá valor nulo (null, em linguagem C), indicando que não há nenhum nó criado.
Perceba que a lista criada como descrito acima somente permite o movimento em um sentido, pois nenhum nó tem o endereço do nó anterior. Essa restrição, não existente na alocação sequencial, dá origem às listas do tipo “simplesmente encadeadas”.
Mas não há óbices a que se crie nos elementos mais um campo ponteiro responsável por guardar o endereço do elemento anterior, apesar do maior gasto de memória. Essas listas são do tipo “duplamente encadeadas” e nesse caso o duplo apontamento permite que o movimento ocorra nos dois sentidos.
A Figura 2 mostra uma representação simbólica de uma lista simplesmente encadeada, enquanto a Figura 3 mostra uma lista com duplo encadeamento.
Figura 2: Lista simplesmente encadeada.
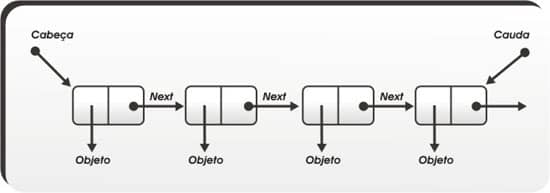
Figura 3: Lista duplamente encadeada.

Comentário
Outra coisa a ser notada é que o mecanismo de alocação dinâmico é mais apropriado para as listas encadeadas.
Portanto, essas listas são geralmente empregadas em situações cujo tamanho só é conhecido em tempo de execução.
Exemplo
Por exemplo, suponha que um programa deseje manter em memória, por uma questão de desempenho, todos os registros de uma agenda telefônica. Cada entrada da agenda corresponderá a um nó. Mas o tamanho da agenda, além de ser variável, só poderá ser determinado por ocasião da execução.
Aliás, o limite para o crescimento de listas encadeadas dinamicamente alocadas é a quantidade de memória disponível no sistema.
Listas simplesmente ou duplamente encadeadas têm vantagens e desvantagens distintas. Além disso, as operações precisam ser ajustadas segundo o tipo de lista. A criação e a desalocação dos nós também são diferentes do que ocorre na alocação sequencial. Veremos essas e outras situações em mais profundidade na próxima subseção.
Listas encadeadas
A primeira coisa que iremos ver é como inserimos um elemento numa lista vazia.
Como dissemos antes, precisamos ter uma referência para a lista. Essa referência é um ponteiro que guardará o endereço do nó cabeça. Logo, para saber se uma lista é vazia, é suficiente testar se o campo “prox” do nó cabeça é nulo.
Se for, a inserção do novo elemento é simples. Basta alocá-lo na memória e fazer o nó cabeça apontar para ele. Apontar significa fazer o campo “prox”, um ponteiro, guardar o endereço de memória do elemento que se quer apontar.
Atenção
Lembremos que a função calloc solicita uma área de memória e, caso haja sucesso em reservar esse espaço, ela retorna o endereço para o mesmo.
Mas, para reservar esse espaço, a função precisa saber o tipo de dado que será armazenado. Bom, os nós guardam os elementos da lista. Mesmo que esses elementos sejam tipos primitivos, nós precisamos que os nós também possuam um campo ponteiro (ou dois, se for uma lista duplamente ligada) para guardar o endereço do próximo elemento (e do anterior, nas listas com dupla ligação). Assim, um nó da lista é um tipo de dado não primitivo.
Para definir um nó em linguagem C, usaremos a função struct, como pode ser visto no Algoritmo 4. Um nó de uma lista duplamente encadeada teria mais um campo ‒ No *ant –, a fim de guardar o endereço do nó anterior.
Algoritmo 4: Definição genérica de um nó de uma lista simplesmente encadeada.
1 struct No {
2 < tipo > campo1;
3 < tipo > campo2;
4 [...]
5 < tipo > campoN;
6 No *prox; }
Repare que definimos uma estrutura chamada “No”, que contém N+1 campos. A instrução struct é usada em linguagem C para instruir o compilador de que os elementos que compõem a estrutura devem ser alocados sequencialmente. Ela define um tipo de dado não primário.
Para nossa discussão, vamos nos concentrar no ponteiro “prox” e por isso vamos usar uma estrutura de nó simples (Código 4), contendo um campo “prox”, do tipo ponteiro; um campo “chave”, do tipo inteiro; e outro campo que é na verdade outra estrutura chamada “Elemento” e cuja definição não faremos. Na prática, “Elemento” poderia estar definida dentro de “No” e a construção dessa forma tem apenas fins didáticos.
Código 4: Definição simples de um nó de lista simplesmente encadeada.
1 struct No {
2 int chave;
3 Elemento elemento;
4 No *prox; }
Agora que definimos um tipo de dado útil para construir nossa lista, podemos retomar nossa abordagem de construção da lista.
Inicialmente, vamos considerar uma lista simplesmente encadeada e não ordenada. Já vimos como proceder se a lista for vazia. Para o caso considerado, mesmo se a lista não for vazia, a inserção de um novo elemento é trivial, pois este pode ser inserido em qualquer ponto.
Então, basta alocar um espaço de memória para o novo elemento, fazer esse novo elemento apontar para o mesmo nó que o nó cabeça aponta e, depois, fazer o nó cabeça apontar para o novo elemento. Desse jeito, estamos inserindo os novos elementos entre o nó cabeça e os nós existentes. Isso é possível, pois não estamos tratando com nenhum tipo especial de lista.
Tratemos agora de como realizar uma busca numa lista encadeada. Como já mencionamos, temos referência apenas para o nó cabeça e, sendo uma lista simplesmente encadeada, só podemos percorrer a lista em um sentido.
Portanto, a busca consiste em, partindo-se do nó cabeça, percorrer toda a lista comparando-se as chaves dos nós. Numa lista não ordenada, essa comparação precisa prosseguir até o fim. O fim da lista é encontrado quando o ponteiro “prox” de um nó tem valor nulo, indicando que não há outros nós encadeados.
Já numa lista ordenada, essa busca pode cessar quando a chave do nó comparado for maior do que a buscada ou quando o fim da lista for atingido. Em ambos os casos, porém, o pior caso será quando toda a lista precisa ser verificada. O Código 5 mostra a implementação em linguagem C de uma função de busca em uma lista ordenada.
Código 5: Busca em lista encadeada ordenada
1 No *buscar ( No *no_cabeca , No **aux, int chave ) {
2 No *atual = no_cabeca -> prox;
3 *aux = no_cabeca;
4 while ( atual != NULL ) {
5 if ( atual -> chave < chave ) {
6 *aux = atual;
7 atual = atual -> prox; }
8 else if ( atual -> chave == chave ) {
9 return atual; } //elemento encontrado
10 else
11 return NULL; } //elemento não encontrado
12 return NULL; } //lista vazia
13 }
Atenção
Uma coisa interessante de se observar nessa função, é que aproveitamos a busca para retornar o endereço do elemento imediatamente anterior ao buscado, caso este não esteja na lista. Isso torna a função de busca útil para a inserção, pois o acesso não pode ser feito diretamente a partir de um simples cálculo de deslocamento, diferentemente da alocação sequencial.
O motivo de termos analisado a busca na lista encadeada ordenada é que este caso particular exibe um comportamento ligeiramente mais complexo. Em uma busca em uma lista não ordenada, a busca necessariamente precisa prosseguir até encontrar o elemento ou o fim da lista. Nesse caso, o procedimento é mais simples, não sendo necessário o teste mostrado na linha 5.
Essa diferença, todavia, não ocorre com os procedimentos de inserção ou remoção. Nesses procedimentos, as operações são as mesmas, embora as listas ordenada e não ordenada guardem diferenças.
Isso é possível uma vez que listas não ordenadas admitem, fora casos particulares de pilhas, filas e deques, a inserção de um elemento em qualquer posição.
Olhemos como a inserção ocorre no Código 6.
Código 6: Inserção em lista encadeada
1 int inserir ( No *no_ant , Elemento novo_elemento , int chave ) {
2 No *aux , *anterior = no_cabeca;
3 No *novo_no = ( No * ) calloc ( 1 , sizeof ( No ) );
4 aux = buscar ( no_cabeca , &anterior , chave );
5 if ( ( novo_no == NULL ) || ( aux != NULL ) )
6 return 0; //falha na inserção
7 else {
8 novo_no -> elemento = novo_elemento;
9 novo_no -> chave = chave;
10 novo_no -> prox = anterior -> prox;
11 anterior -> prox = novo_no;
12 return 1; //inserção bem sucedida }
13 }
Agora, observe as linhas 8 a 11 do código mostrado. É nelas que a inserção ocorre.
Nas linhas 8 e 9, o novo nó recebe os valores a serem inseridos. Esse nó, criado na linha 3, corresponde até esse ponto a um espaço de memória preenchido com os novos valores, mas sem qualquer ligação com a lista.
Na linha 10, fazemos o campo “prox” do novo nó (“novo_no”) apontar para a mesma região de memória que é apontada por “prox” em “anterior”.
O próximo passo, linha 11, consiste em fazer o campo “prox” de “anterior” apontar para “novo_no”. Em outras palavras, após a linha 11 teremos inserido “novo_no” entre o nó “anterior” e aquele apontado pelo seu campo prox. Esse procedimento funciona indistintamente para listas ordenadas ou não.
A remoção é igualmente simples. No caso das listas encadeadas, não precisamos sobrescrever o elemento removido com o posterior, pois esse pode ser efetivamente desalocado.
Assim, a remoção consiste em duas ações básicas: Fazer o nó anterior ao nó que será removido apontar para o nó posterior deste e desalocar o nó removido, o que na linguagem C é feito pela instrução free.
Vejamos o Código 7, que implementa a remoção de um nó em uma lista encadeada.
Código 7: Remoção em lista encadeada.
1 remover ( No *no_cabeca , int chave ) {
2 No *aux , *anterior = no_cabeca;
3 aux = buscar ( no_cabeca , &anterior , chave );
4 if ( aux != NULL ) {
5 anterior -> prox = aux -> prox;
6f ree ( aux );
7 return 1; //remoção bem sucedida
8 } else
9 return 0; //falha remoção
10 }
Essas operações se aplicam à lista simplesmente encadeada. Mas, como vimos antes, podemos construir listas com duplo encadeamento. Para isso, a estrutura do nó mostrado no Código 4 precisa ser modificada para incluir mais um campo do tipo ponteiro, que será usado para apontar para o nó predecessor, conforme observamos no Código 8 (campo “ant”).
Código 8: Definição de um nó para lista duplamente encadeada.
1 struct No {
2 int chave;
3 Elemento elemento;
4 No *prox;
5 No *ant; }
Obviamente os procedimentos de inserção e remoção precisam ser adequados. Uma lista duplamente encadeada torna desnecessário manter um ponteiro para o antecessor do nó buscado e exige mais operações na inserção e na remoção.
O procedimento de busca (Código 5) funciona mesmo em listas duplamente encadeadas, mas para estas, ele pode ser simplificado. Mas a existência de um duplo encadeamento não altera a complexidade das operações de inserção, busca e remoção.
Da mesma maneira que na alocação sequencial, podemos transformar uma lista encadeada em circular de forma simples. Basta que o último nó da lista passe a apontar para o nó cabeça. Isso significa fazer o campo “prox” do último nó apontar para o nó cabeça.
Todavia, isso não altera a unidirecionalidade do percurso na lista, que só pode se dar do nó cabeça em direção aos nós subsequentes.
Para permitir que o percurso numa lista circular se dê em dois sentidos, faz-se necessário usarmos uma lista duplamente encadeada. Com uma lista desse tipo, para que ela se torne circular, além de fazermos o último nó apontar para o nó cabeça, precisamos fazer o campo “ant” do nó cabeça apontar para o último nó da lista.
APLICANDO LISTAS ENCADEADAS
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Identificar os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de pilhas
Tipo de lista: Pilha
Veremos agora um tipo particular de lista chamada pilha. Uma pilha é um tipo de lista na qual as operações de inserção, remoção e acesso ocorrem sempre numa mesma extremidade, chamada de topo.
Comentário
Por essa razão, apenas a posição do topo precisa ser monitorada.
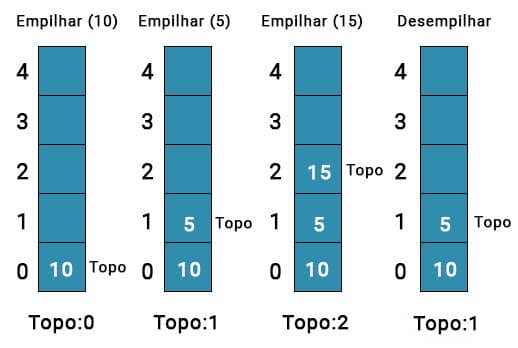
Uma pilha segue a regra “O último a chegar é o primeiro a sair”, também conhecida pela sigla LIFO, do inglês Last In, First Out. Colocando de outra maneira, a remoção ocorre na ordem inversa da inserção. Devido à essa característica, pilhas têm a propriedade de inverter sequências.

Teoria na prática
Vamos proceder a um exemplo para ilustrar a propriedade citada. Textualmente, representaremos uma pilha pelos símbolos de chaves. O símbolo “{“ representa a base da pilha. Já o símbolo “}” marca o topo da pilha, onde as operações ocorrem.
Considere que você tem os seguintes elementos que deseja inserir numa pilha: a, b, c, d, e. Os elementos são lidos da esquerda para a direita em sequência.
Vejamos a execução do empilhamento (Tabela 1) de todos os itens, seguida do desempilhamento (Tabela 2).
|
Tabela 1: Empilhamento |
||
|---|---|---|
|
Pilha |
Operação |
Sequência de Entrada |
|
{ } |
push (a) |
a, b, c, d, e |
|
{ a } |
push (b) |
b, c, d, e |
|
{ a , b } |
push (c) |
c, d, e |
|
{ a, b, c } |
push (d) |
d, e |
|
{ a, b, c, d } |
push (e) |
e |
|
{ a, b, c, d, e} |
||
|
Tabela 2: Desempilhamento |
||
|---|---|---|
|
Pilha |
Operação |
Sequência de Saída |
|
{ a, b, c, d, e} |
pop ( ) |
|
|
{ a, b, c, d } |
pop ( ) |
e |
|
{ a, b, c } |
pop ( ) |
e, d |
|
{ a, b } |
pop ( ) |
e, d, c |
|
{ a } |
pop ( ) |
e, d, c, b |
|
{ } |
e, d, c, b, a |
|
Tabelas 1 e 2. Fonte: O Autor.
Olhando o exemplo, algumas considerações merecem ser feitas
Pilhas possuem diversas aplicações em informática. A característica de inversão de cadeias tem grande utilidade, permitindo funcionalidades que facilitam o cotidiano, como a funcionalidade de desfazer ações existentes em diversos programas, por exemplo. Cada ação realizada no programa, é inserida na pilha. Quando acionamos a função de desfazer, as ações são desfeitas na ordem inversa em que ocorreram, isto é, da mais recente para a mais antiga. Isso é feito desempilhando as ações a serem revertidas.
Outro importante exemplo de uso de pilhas está relacionado diretamente com a execução de programas computacionais.
Pilhas são empregadas durante a execução de qualquer programa de computador, para controlar as trocas de contexto.
Exemplo
Quando uma função é chamada durante a execução do programa, o contador de programa é desviado para outra posição de memória, inserindo o endereço de retorno em uma pilha. Isso é necessário para permitir que a execução do programa seja retomada a partir do ponto no qual foi desviada. Quando a função termina sua execução, o contador de programa desvia para o último endereço de retorno empilhado e o retira da pilha de execução. Caso uma segunda função seja chamada antes do término da primeira, um novo desvio é feito pelo contador de programa e um novo endereço de retorno é empilhado. Conforme as funções forem terminando sua execução, o contador de programa vai retornando aos endereços empilhados e retirando-os da pilha de execução.
Outros casos, como a conversão para número binário, podem ser identificados, mas os exemplos dados devem ser suficientes para mostrar-lhe a importância dessa estrutura de dados.
Em nosso exemplo, utilizamos uma representação genérica de pilha. Mas não se esqueça de que se trata de um tipo particular de lista. Ou seja, da mesma maneira que as listas, podemos implementar a pilha através de alocação sequencial ou encadeada, com diferentes vantagens e desvantagens. Nas próximas subseções, nós veremos essas possibilidades mais detidamente.
Pilhas em alocação sequencial
Uma limitação que você já deve estar imaginando é que pilhas implementadas através de alocação sequencial estão sujeitas à restrição de memória correspondente ao tamanho do vetor definido.
Assim, é preciso realizar testes que impeçam o desempilhamento em uma pilha vazia (underflow) e o empilhamento em uma pilha cheia (overflow).
Apesar disso, operacionalizar uma pilha com alocação sequencial é simples. A operação de inserção (empilhamento) sempre ocorre na extremidade, assim como a remoção (desempilhamento). Mais ainda, ambas ocorrem na mesma extremidade. Com isso, não temos a sobrecarga de mover os demais elementos do vetor, como seria se fosse possível fazer tais operações no interior.
Semelhantemente à lista genérica alocada sequencialmente, o desempilhamento não desaloca de fato a memória. O que é feito, nesse caso, é um controle de qual posição do vetor representa o topo. As posições do início até o topo são consideradas ocupadas. As posições maiores que o topo até o limite do vetor, são posições disponíveis, que podem receber elementos.
Portanto, empilhar significa incrementar o topo, e desempilhar, decrementá-lo.
A Figura 5 ilustra essas operações para um vetor genérico.
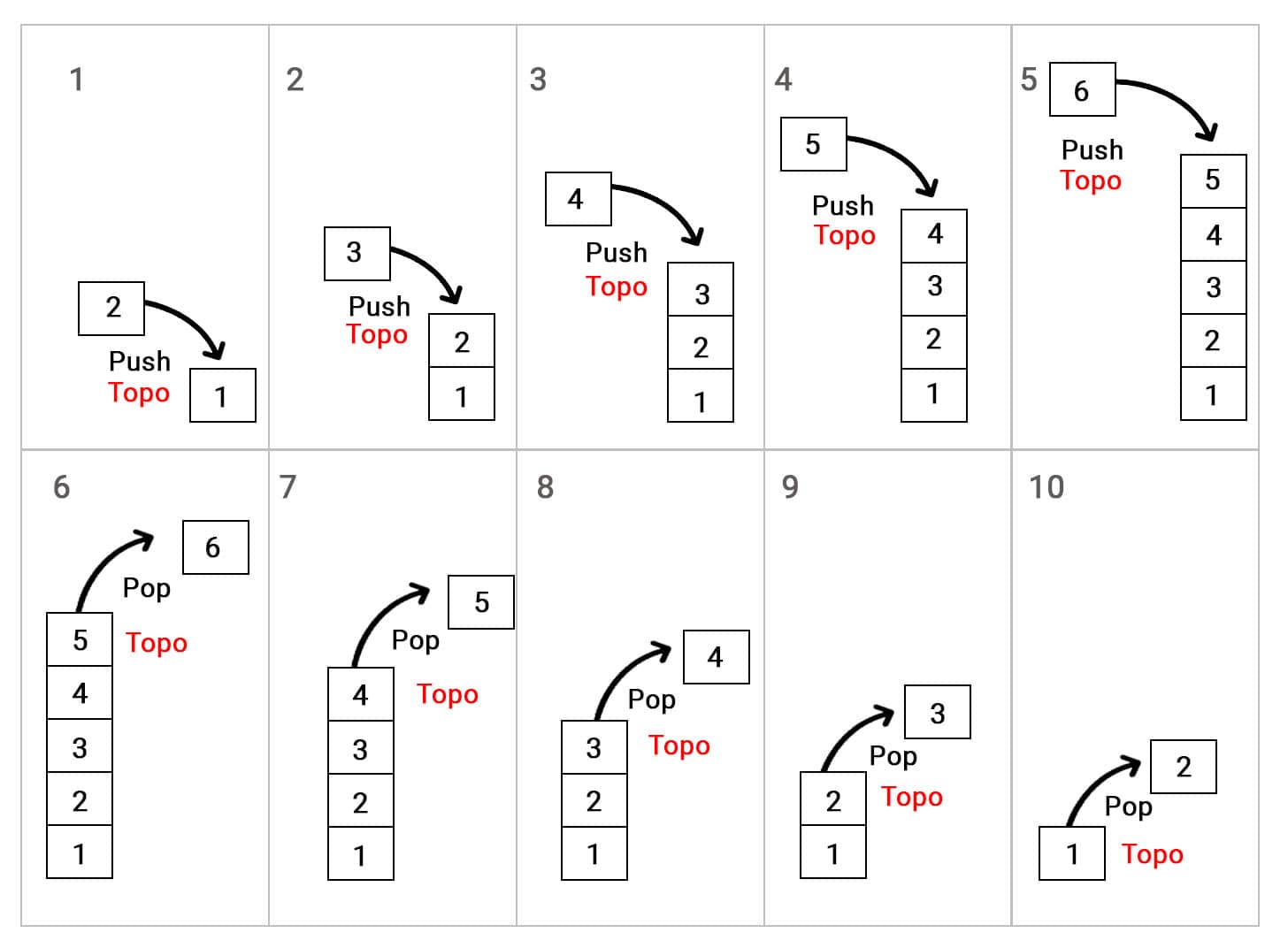
Vamos verificar, primeiramente, como se processa a operação de empilhamento em uma pilha vazia.
Para pilhas implementadas por meio de vetores, o topo será controlado por uma variável do tipo inteiro chamada de “topo”. A finalidade dessa variável é guardar o índice do vetor que corresponde ao topo da pilha.
Em linguagem C, o vetor inicia em 0 (zero), então convencionaremos que uma pilha vazia será indicada pelo valor da variável “topo” igual a -1.
Antes de inserirmos um elemento na pilha, precisamos verificar se há posições desocupadas no vetor. Isso é feito comparando-se o valor de “topo” com o tamanho do vetor, o qual é conhecido a priori.
Caso haja espaço, a variável “topo” deve ser incrementada e o novo elemento inserido no novo topo. Esse procedimento pode ser visto no Código 9. Nesse código, MAX_PILHA é o tamanho do vetor que implementa a pilha. A falha ocorrerá se for tentado o empilhamento de um elemento em uma pilha cheia.
Código 9: Função de empilhamento.
1 int push ( Elemento elemento ) {
2 if ( topo < ( MAX_PILHA – 1 ) ) {
3 topo++;
4 pilha [ topo ] = elemento;
5 return 1; //sucesso
6 } else
7 return 0; //falha
8 }
O desempilhamento é igualmente uma operação simples. Antes de se remover um elemento da pilha, é preciso verificar-se se ela está vazia. Dessa maneira, se o valor da variável “topo” for maior ou igual a zero, o desempilhamento pode ocorrer. Caso contrário, ele deve ser impedido para se evitar o underflow.
Antes de desempilhar o elemento do topo, esse é acumulado em uma variável temporária para que seu valor possa ser recuperado. Em seguida, basta decrementarmos a variável “topo”, indicando que a posição passou a estar disponível para escrita. Observe a implementação do Código 10.
Código 10: Função de desempilhamento.
1 Elemento pop ( void ) {
2 Elemento valor_recuperado;
3 if ( topo >= 0 ) {
4 valor_recuperado = pilha [ topo ];
5 topo--;
6 return valor_recuperado;
7 } else
8 return NULL; //falha
9 }
Voltando ao nosso exemplo do empilhamento dos elementos a, b, c, d, e.
Antes do primeiro empilhamento, “topo” teria valor -1. Vamos agora considerar que nosso vetor tem 3 posições, isto é, os índices variam de 0 a 2.
A primeira chamada push ( a ), incrementará o valor de “topo” e colocará o elemento “a” na posição 0 (zero) do vetor.
A execução subsequente de push ( b ) e push ( c ), fará com que “topo” tenha valor 2.
Logo, a execução em seguida de push ( d ), será desviada na linha 2 do Código 9, pois topo (2) é igual ao valor da expressão MAX_PILHA (3) – 1.
Entretanto, se executarmos a função pop ( ), “c” será removido da pilha, e o valor de “topo” será decrescido para 1.
Após isso, push ( d ) conseguiria empilhar “d”, tornando a pilha novamente cheia.
Vamos considerar agora o desempilhamento. A execução de pop ( ), irá desempilhar “d”, decrementando “topo”.
Atenção
Não se esqueça que, de fato, “d” permanece no vetor, mas agora a sua posição poderá ser sobrescrita.
A sequência pop ( ), pop ( ) esvaziará completamente a pilha, de forma que a tentativa de se executar uma quarta vez seguida a função pop ( ) não será possível. Na quarta execução, “topo” valerá -1, desviando a execução na linha 3 do Código 10.
Pilhas em alocação dinâmica
No caso de pilhas em alocação encadeada, a situação é diferente. O desempilhamento em uma pilha vazia ainda precisa ser prevenido, contudo, como o limite para empilhamento é a memória disponível, não há necessidade de se verificar a tentativa de empilhamento em uma pilha cheia.
Nesse caso, basta identificar-se quando não for possível uma nova alocação de memória para um novo elemento da pilha.
As operações são muito simples, por se tratar de um caso particular. Apesar de podermos usar listas duplamente encadeadas, a pilha é eficientemente implementada por listas simplesmente encadeadas, não se justificando o uso extra de memória. Também não utilizaremos o nó cabeça – nó especial, criado para facilitar as operações em lista – por ser desnecessário.
Para entendermos como uma pilha é implementada por uma lista de encadeamento simples, vamos começar considerando uma pilha vazia.
Como precisamos sempre saber quem é o topo, utilizaremos uma variável ponteiro chamada “topo”, cuja finalidade é apontar para o último elemento inserido na pilha.
Inicialmente, na pilha vazia, “topo” terá valor nulo.
Comentário
Como dissemos, tentativas de desempilhar da pilha nessa situação devem ser impedidas, o que é levado a termo pelo teste do valor de “topo”.
A execução de uma operação de empilhamento - push ( ) ‒ envolve o recebimento do elemento a ser empilhado, seguido da alocação de um nó para acumular esse valor.
Uma vez que esse nó tenha sido criado, o seu campo “prox” deverá apontar para o mesmo endereço apontado por “topo”.
Sendo a primeira operação em uma pilha vazia, logicamente o campo “prox” desse nó terá valor nulo. Em seguida, o ponteiro “topo” precisa ser atualizado, passando a apontar para o novo nó empilhado.
É fácil notar que a repetição de operações push ( ) vai inserindo os nós na lista, sempre com o novo nó apontando para o último nó inserido.
Assim, a operação de desempilhamento - pop ( ) - é trivial. Basta caminhar no sentido da lista. Ou seja, a cada operação pop ( ), o ponteiro “topo” passa a apontar para o campo “prox” do nó desempilhado e, após a recuperação do elemento armazenado no nó, este deve ser desalocado.
A operação pop ( ) no último elemento da pilha fará “topo” assumir valor nulo, indicando uma lista vazia. A Figura 6 ilustra a forma como essas operações se processam.
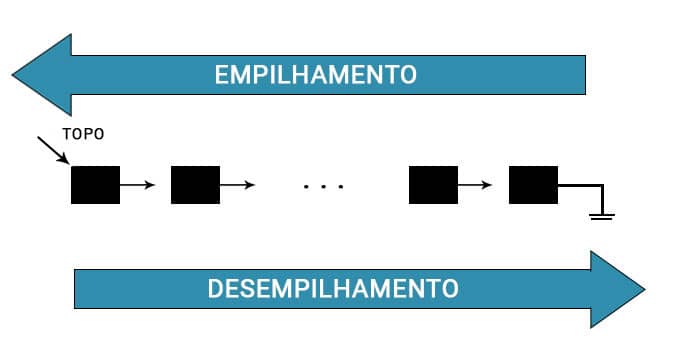
A função de empilhamento pode ser vista no Código 11.
Como estamos lidando com alocação encadeada, precisamos alocar a memória necessária sempre que vamos empilhar um elemento. Isso ocorre na linha 2.
A linha 3 verifica se a alocação foi bem sucedida, caso em que a execução segue para a linha 4. A não alocação pode indicar o esgotamento da memória, tornando inviável novos empilhamentos.
As linhas 4 a 6 são as que efetivamente executam o empilhamento. Na linha 4, o novo elemento é guardado na memória alocada. Em seguida, linha 5, o novo nó passa a apontar para o atual topo da pilha. A atualização do topo, passando a apontar para o nó inserido, se dá na linha 6.
Código 11: Função de empilhamento.
1 int push ( Elemento elemento ) {
2 No *novo_no = ( No * ) calloc ( 1 , sizeof ( No ) );
3 if ( novo_no != NULL ) {
4 novo_no->elemento = elemento;
5 novo_no -> prox = topo;
6 topo = novo_no;
7 return 1; //sucesso
8 } else
9 return 0; //falha
10 }
O Código 12 mostra a função de desempilhamento.
Veja que utilizamos um ponteiro auxiliar (aux). O objetivo deste é permitir a desalocação do nó desempilhado.
Na linha 4, testamos para ver se a pilha é vazia, situação em que o desempilhamento geraria um underflow.
Caso não seja, o desempilhamento é possível e é executado pelas linhas 7 e 8. Em 7, o ponteiro topo é atualizado, passando a apontar para o nó seguinte ao que será desempilhado. A linha 8 realiza a liberação de memória do espaço previamente ocupado pelo nó removido.
O elemento guardado no nó desempilhado é acumulado em “elemento_recuperado”, sendo retornado pela função.
Código 12: Função de desempilhamento.
1 int pop ( void ) {
2 No *aux;
3 Elemento elemento_recuperado;
4 if ( topo != NULL ) {
5 elemento_recuperado = topo->elemento;
6 aux = topo;
7 topo = topo->prox;
8 free ( aux );
9 return elemento_recuperado;
10 } else
11 return NULL;
12 }
Observe que, em ambos os casos, o número de passos executados é fixo.
Pilhas e expressões aritméticas binárias
A manipulação de expressões aritméticas é um tema importante, que requer uma forma adequada de se representar computacionalmente tais expressões.
Usualmente, expressões aritméticas possuem operadores, que representam as operações aritméticas, operandos, sobre os quais os operadores atuam, e delimitadores, utilizados para estabelecer a precedência das operações.

Teoria na prática
Você pode se surpreender, mas há mais de uma forma de se escrever uma expressão aritmética.
A forma tradicional, com os operadores posicionados entre seus operandos é chamada de forma infixa. Essa notação, porém, é ambígua, o que obriga o estabelecimento de regras e o uso dos delimitadores.
Veja a expressão 2 * 3 / 4 * 2.
Você consegue calcular o resultado?
Se considerarmos que o produto e a divisão possuem mesma precedência, passamos a ter dois resultados possíveis: 0,75 e 3, dependendo da ordem em que executemos as operações:
- 2 * ( 3 / 4 ) * 2 = 3
- ( 2 * 3 ) / ( 4 * 2 ) = 0,75
Assim, podemos ver que, para eliminar a ambiguidade, as regras de precedência dos operadores aritméticos não são suficientes. Precisamos lançar mão dos delimitadores, a fim de eliminar a ambiguidade.
A notação infixa, ou tradicional, ao ser modificada pelos delimitadores, é também chamada de notação parentizada. A dificuldade de se avaliar expressões tradicionais ou parentizadas advém, justamente, do fato de que a prioridade das operações não segue a ordem de ocorrência.
Outra forma de se escrever tais expressões é a chamada notação polonesa. Nesta forma, os operadores aparecem imediatamente antes dos operandos, o que evita ambiguidades.
A expressão ( 2 * 3 ) / ( 4 * 2 ) é escrita em notação polonesa como / * 2 3 * 4 2. Isso indica que a divisão será aplicada ao produto entre 2 e 3 e entre 4 e 2. Ou seja, as operações podem ser processadas na ordem em que aparecem, sem ambiguidade e sem necessidade de parentização.
Há também a notação polonesa reversa, ou pós-fixa, na qual o operador aparece imediatamente após os operandos.
Essa discussão serve para contextualizar a aplicação de pilhas que são utilizadas para permitir a conversão da notação parentizada para a polonesa reversa. Essa conversão não altera a ordem dos operandos, ou seja, estes podem ser copiados diretamente para a nova expressão. Segundo Pereira (2016), os operadores, todavia, devem refletir a prioridade estabelecida pela parentização. Como a ocorrência de um operador na notação pós-fixa implica a execução da operação, estes deverão ser copiados quando o parêntese de fechamento correspondente for encontrado.
A notação polonesa reversa permite calcular o valor de uma expressão percorrendo-a e empilhando os operandos.
Quando um operador é encontrado, desempilham-se dois operandos, e o resultado da operação realizada é empilhado.
Ao término, o valor da expressão estará registrado no topo da pilha.
Por exemplo, considere a expressão em notação pós-fixa 2 3 * 4 2 * /.
Mão na Massa
Passo 1
Ao percorrê-la, primeiro seria empilhado o 3, depois o 2. A seguir, seria encontrado o símbolo do produto, causando o desempilhamento de 2 e 3, a execução do produto 2 * 3 e o empilhamento do resultado (6).
Passo 2
Continuando, seriam empilhados 4 e 2. A pilha agora seria formada por 6, 4, 2, estando 2 no topo. Ao ser encontrado o segundo operador de produto (*), 4 e 2 seriam desempilhados, 4 * 2 seria executada e o resultado, 8, seria empilhado.
Passo 3
Nesse ponto, a pilha seria 6, 8. Continuando a varredura, encontraríamos o sinal de divisão ( / ), levando ao desempilhamento de 6 e 8 e à execução de 8 / 6.
A seguir, seria empilhado o resultado dessa divisão, 0,75, que é o resultado da expressão.
APLICANDO PILHAS
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 4
Reconhecer os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de filas
Tipo de lista: Fila
Uma fila é um tipo particular de lista mais elaborado do que a pilha. No caso de filas, as operações de inserção e remoção ocorrem em duas extremidades.
As inserções sempre ocorrem no final ou retaguarda da fila, enquanto as remoções são executadas na outra extremidade, denominada início.
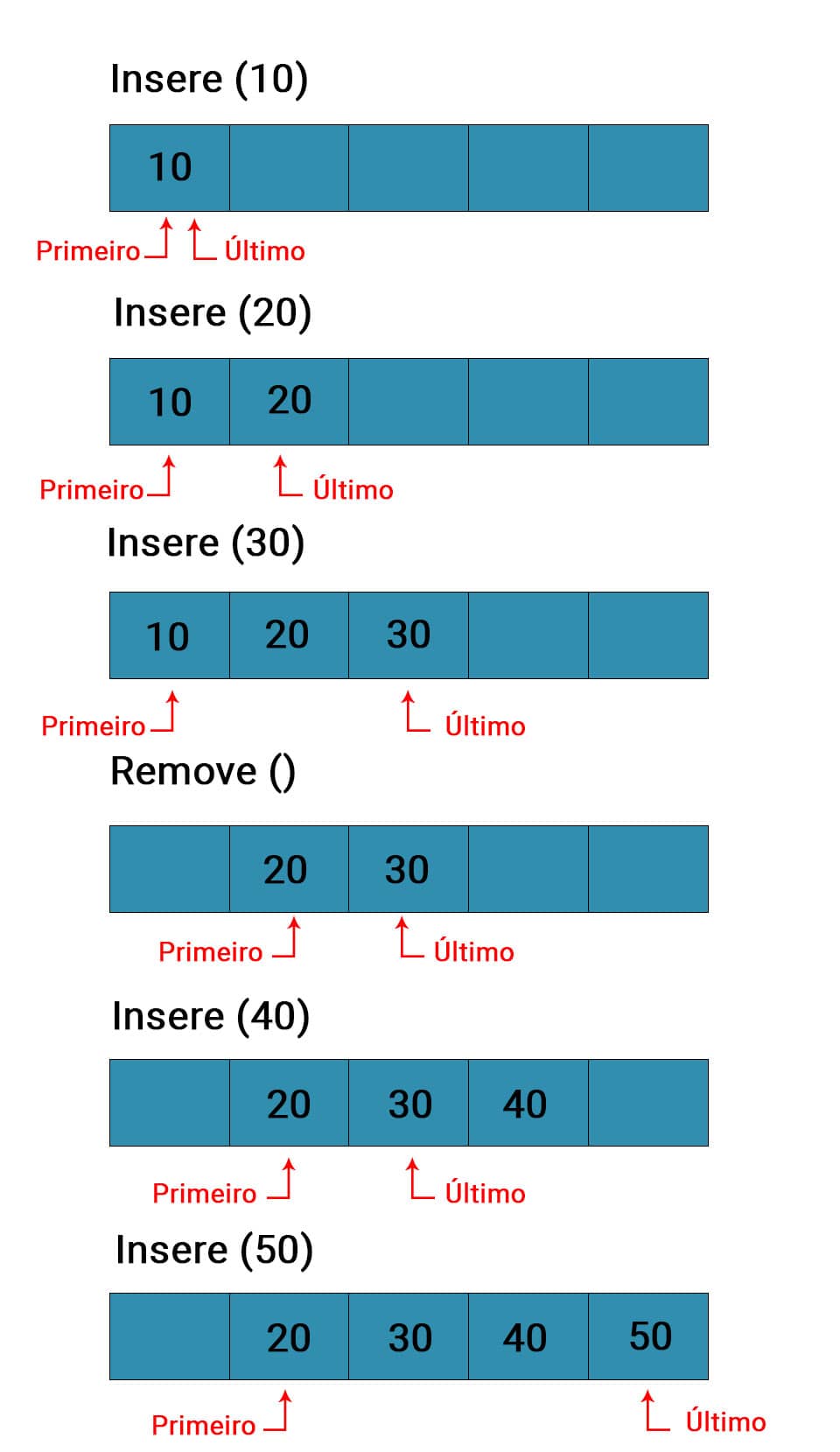
As filas obedecem à regra “O primeiro a chegar é o primeiro a sair”, também chamada de FIFO, do inglês first in, first out. Por essa razão, precisamos de dois controles para a fila:
- Um para identificar o início da fila.
- Outro para marcar o seu término.
Comentário
Se uma pilha tem a capacidade de inverter a ordem, a fila tem a propriedade de manter a ordem dos elementos.
Isso decorre do fato de que as remoções ocorrem na mesma ordem que as inserções. Ilustremos essa situação.
Suponha que vamos enfileirar o conjunto de entrada a, b, c, d, e. Usaremos a mesma simbologia de pilhas, mas, nesse caso, o símbolo de “{“ representa o início da fila e o símbolo de “}” o seu final.
Inicialmente, a fila está vazia e as entradas são lidas na ordem em que aparecem. A Tabela 3 mostra o processamento das entradas pela fila. De maneira similar à pilha, a operação de enfileirar (enqueue) recebe como parâmetro o elemento a ser inserido na fila, mas a operação de desenfileirar (dequeue) não possui parâmetro.
Tabela 3: Processamento de uma cadeia através de uma fila.
|
Entrada |
Enfileirar |
Fila |
Desenfileirar |
Saída |
|---|---|---|---|---|
|
a, b, c, d, e |
enqueue ( a ) |
{ } |
||
|
b, c, d, e |
enqueue ( b ) |
{ a } |
||
|
c, d, e |
enqueue ( c ) |
{ a, b } |
||
|
d, e |
enqueue ( d ) |
{ a, b, c } |
||
|
e |
enqueue ( e ) |
{ a, b, c, d } |
||
|
{ a, b, c, d, e } |
dequeue () |
|||
|
{ b, c, d, e } |
dequeue ( ) |
a |
||
|
{ c, d, e } |
dequeue ( ) |
a, b |
||
|
{ d, e } |
dequeue ( ) |
a, b, c |
||
|
{ e } |
dequeue ( ) |
a, b, c, d |
||
|
{ } |
a, b, c, d, e |
Tabela 3. Fonte: O Autor.
Se você observar atentamente a tabela, notará que em nossa fila de exemplo as inserções ocorreram pela direita, fazendo a fila crescer nesse sentido. Já as remoções se deram pela esquerda, provocando o seu encurtamento.
A esquerda é o início da fila e a direita é o fim. Isso pode gerar um problema para filas em alocação sequencial, o que torna sua implementação nesse caso ligeiramente mais complexa. Vamos explorar isso na subseção que trata de filas alocadas sequencialmente, mas procure refletir desde já e tente identificar o problema.
Assim como a pilha, a fila tem ampla aplicação.
Exemplo
Considere, por exemplo, a execução de programas nas CPU com múltiplos núcleos. Desconsideremos, por questão de simplicidade, a existência de prioridades de execução. Quando um programa é iniciado, cria-se um processo que é colocado numa fila de execução.
À medida que os núcleos finalizam suas tarefas, os processos são retirados da fila e postos em execução no núcleo vago, garantindo-se, assim, que todos sejam atendidos. Na prática, essa sistemática é bem mais elaborada, pois há prioridades de execução e preempção, por exemplo. A prioridade de execução pode levar um processo a ser atendido antes de outro que foi enfileirado primeiro.
Já a preempção pode tirar de execução um processo, antes deste terminar, permitindo ao núcleo atender a outro processo. Contudo, todas essas características são implementadas através de filas (por exemplo, uma fila de prioridades), não havendo violação do princípio FIFO. O agendamento de processos faz largo emprego de filas, com estruturas bem complexas, como filas multinível.
Outro exemplo do uso de filas, também se desconsiderando a existência de parâmetros que alterem a ordem de execução, é a implementação de uma fila de impressão. Nesse exemplo, múltiplos usuários podem enviar diversos arquivos para a impressão num mesmo equipamento. Esses arquivos, ao serem recebidos, são colocados numa fila e são impressos seguindo a ordem de chegada. Ou seja, o primeiro a ser recebido é o primeiro a ser impresso.
Há vários outros exemplos do uso de filas, mas estes devem ter mostrado sua relevância e utilidade. Vamos olhar, nas próximas subseções, os detalhes relativos à implementação de filas em alocação sequencial e em alocação encadeada.
Filas em alocação sequencial
Como vimos, a implementação de filas demanda o controle de duas posições, o início e o fim.
A posição final é aquela na qual ocorrem as inserções, e por isso, por onde a lista aumenta. A posição inicial é onde ocorrem as remoções, sendo por onde a fila é encurtada. Isso acarreta um problema para a alocação sequencial.
Imagine uma fila implementada através de um vetor com N posições. Inicialmente, a fila está vazia. Após a chegada do primeiro elemento, a primeira posição do vetor é ocupada. Com a chegada de um segundo elemento, ocupa-se a segunda posição. Suponha que, nesse momento, um elemento seja retirado da fila. Nesse caso, o início da fila, que era a primeira posição, torna-se a segunda posição (a primeira agora está desocupada).
Comentário
Perceba que, ao longo do tempo, conforme inserções e remoções sejam feitas na fila, esta realiza um deslocamento aparente no sentido da sua retaguarda. As posições inicial e final têm índices sucessivamente maiores.
Mesmo se as inserções forem superadas pelas remoções, é possível afirmar-se que, com certeza, a posição inicial se deslocará em direção à retaguarda. Assim, duas situações podem ocorrer:
- Novas inserções podem ser impedidas, devido ao fim da fila atingir o fim do vetor.
- O desperdício de memória relativo aos espaços desocupados antes do início.
Uma possível solução para essa questão seria deslocar todos os elementos da fila uma posição em direção ao início, sempre que houver uma remoção. Dessa forma, o início da fila seria sempre mantido na primeira posição do vetor e, de fato, quando uma inserção não fosse possível seria devido ao vetor estar preenchido.
Outra abordagem possível é implementar a fila através de uma lista circular. Nesse caso, o vetor comporta-se como se após a última posição, estivesse a primeira. Ou seja, uma vez que o fim da fila atinja o fim do vetor, uma nova inserção será possível se a primeira posição estiver livre.

Teoria na prática
Para ilustrar, retomemos o exemplo dado no primeiro parágrafo dessa subseção, considerando uma fila com implementação circular e um vetor cuja posição inicial tenha índice 1.
Utilizemos uma variável “I” para controlar a posição inicial da fila e “F” para a posição do fim. Vimos que as inserções e remoções causariam um deslocamento aparente na fila. Imagine agora que uma inserção foi feita, ocupando a N-ésima posição do vetor, e que houve pelo menos uma remoção da fila. Nessa situação, sabemos que F = N e I > 1.
Caso se tente fazer uma nova inserção, esta terá que ser feita na posição seguinte à N-ésima, que no caso da lista circular, é a primeira posição do vetor. Como já houve ao menos uma remoção, podemos afirmar que a primeira posição está disponível.
Nessa situação, o fim da fila passa a ser a primeira posição, nos levando a F = 1 e I > 1. Portanto, I > F, ou seja, temos uma situação na qual o índice da posição inicial da fila é maior do que o índice da posição final.
A situação anterior aborda a inserção, mas a remoção também se comportará de forma semelhante. Consideremos que após um certo número de operações, o início da fila continuou se deslocando até que I = N (o início da fila está na N-ésima posição). O comportamento no caso de uma nova remoção da fila é mover o início da fila para a primeira posição do vetor (pois esta é a posição subsequente à N-ésima numa lista circular), de forma que I ≤ F.
É preciso perceber que quando a fila só tem um elemento, I = F. O valor de I e F, nesse caso, dependerá das operações realizadas, pois o elemento pode estar em qualquer posição da lista.
Uma fila vazia, por sua vez, deverá ser identificada por algum valor de I e F convencionados e fora dos limites do vetor (por exemplo, I = F = -1 ). A remoção do único elemento existente em uma fila deverá, dessa forma, fazer com que I e F tenham o valor igual a -1, que é o valor convencionado para indicar lista vazia. Você não pode deixar de perceber que apenas se alguma das variáveis, I ou F, for diferente do valor convencionado para fila vazia, a outra também o será obrigatoriamente. Veja, quando um elemento é inserido numa fila vazia, I = F = 1.
Um caso que talvez esteja lhe fazendo pensar é como identificar que a fila está cheia. Para determinarmos isso, precisamos considerar duas situações distintas:
- A primeira é relativa ao caso em que a fila simplesmente recebe novos elementos, sem nenhuma remoção. Nesse caso, a fila estará cheia se I = 1 e F = N.
- A segunda situação é quando houve remoções na fila, o que fez com que I > 1. Nessa hipótese, não é suficiente testar se F = N, pois há espaço livre antes de I (afinal, é uma lista circular).
A fila se encontrará cheia numa situação como essa se, e somente se, I = F + 1. Ou seja, caso o início da fila esteja na posição imediatamente posterior ao seu fim.
Você pode imaginar que a fila cresceu até que seu fim tocou seu início, completando o círculo. No raciocínio desenvolvido até agora, utilizamos um vetor cujo índice da primeira posição é 1. No caso de linguagens, como a C, o vetor inicia-se em 0 (zero), o que deve ser considerado para ajustar a lógica. O Código 13 e o Código 14 exibem, respectivamente, a implementação das funções para enfileirar (enqueue) e desenfileirar (dequeue). MAX_FILA é o tamanho máximo do vetor.
Código 13: Função enfileirar.
1 int enfileirar ( Elemento elemento ) {
2 if ( !( ( inicio == 0 && fim == MAX_FILA - 1 ) || ( inicio == fim + 1 ) ) ) {
3 if ( ( fim == MAX_FILA - 1 ) || ( fim == -1 ) ) {
4 fila [ 0 ] = elemento;
5 fim = 0;
6 if ( inicio == -1 )
7 inicio = 0;
8 } else {
9 fila [ ++fim ] = elemento;
10 return 1; //sucesso
11 } else
12 return 0; //falha
13 }
No Código 13, a linha 2 verifica se a fila está cheia. Em seguida, a linha 3 verifica se o fim da fila está na última posição do vetor ou se a fila é vazia. Já a linha 9 é executada se o fim da fila não estiver na última posição do vetor e a fila não for vazia. E a linha 12 indica a falha caso seja tentada uma inserção em uma fila cheia.
Código 14: Função desenfileirar.
1 Elemento desenfileirar ( void ) {
2 Elemento elem_temp;
3 if ( inicio != -1 ) {
4 elem_temp = fila [ inicio ];
5 if ( inicio == fim )
6 fim = inicio = -1;
7 else if ( inicio == MAX_FILA - 1 )
8 inicio = 0;
9 else {
10 inicio++;
11 return elem_temp;
12 } else
13 return NULL; //falha
14 }
Na função de desenfileiramento mostrada no Código 14, a linha 3 evita a remoção em uma lista vazia e a linha 5 visa a identificar se após a retirada do elemento da fila, ela vai se tornar vazia. A linha 7 implementa a circularidade na remoção, enquanto a linha 10 corresponde às remoções nas demais situações.
Comentário
Observe que, em ambos os casos, o número de passos dos algoritmos não varia. Os elementos também não são desalocados de fato. Como em todos os casos que já vimos de alocação sequencial, apenas as posições dos elementos removidos se tornam livres para serem sobrescritas.
Filas em alocação dinâmica
Vejamos agora o caso de fila implementada em alocação encadeada.
Relembrando o comportamento das filas, notamos que não precisamos percorrer a lista para executar as operações de inserção ou remoção. Uma vez que estas sempre ocorrem nas extremidades, basta mantermos uma referência para essas posições, da mesma maneira que no caso de alocação sequencial.
Isso nos remete à mesma situação da pilha, cuja implementação através de lista simplesmente encadeada mostra-se suficiente e vantajosa. O mesmo ocorre no caso das filas. Embora possamos implementá-las através de uma lista duplamente encadeada, não há vantagem que justifique o gasto extra de memória. Logo, nossa fila será implementada através de uma lista simplesmente encadeada, sem nó cabeça.
Comentário
Para sermos capazes de realizar inserções e remoções, precisaremos manter referências para o início e o fim da fila. Já que estamos tratando de alocação encadeada, as variáveis responsáveis por esse controle serão do tipo ponteiro.
Usemos o ponteiro “inicio” para referenciar o início da fila e o ponteiro “fim” para o seu final. Incialmente, vamos definir que a lista vazia será caracterizada por inicio = fim = NULL. O comportamento de filas em alocação encadeada guarda alguma similaridade com o caso de alocação sequencial. As diferenças ficam por conta das duas situações apresentadas no primeiro parágrafo da subseção anterior.
- Novas inserções podem ser impedidas, devido ao fim da fila atingir o fim do vetor.
- O desperdício de memória relativo aos espaços desocupados antes do início.
Consideremos, por exemplo, a situação quando o primeiro elemento for inserido numa fila vazia. Após a inserção, teremos que ambas as variáveis (“inicio” e “fim”) apontarão para o mesmo endereço de memória. Esse endereço será o correspondente ao espaço de memória alocado para o elemento inserido.
Se novas inserções ocorrerem, a variável “inicio” manter-se-á apontando para o primeiro elemento inserido, e a variável “fim” passará a apontar para o novo nó criado.
A remoção, por sua vez, provocará a desalocação do nó apontado por “inicio”, forçando com que a variável passe a apontar para o nó seguinte. A remoção do único elemento na fila, situação em que inicio = fim, torna novamente inicio = fim = NULL.
Saiba mais
A implementação através de listas encadeadas contorna ambos os problemas que indicamos na alocação sequencial. O desperdício de memória é evitado, pois sempre que um elemento é retirado da fila, ele é efetivamente desalocado e a memória ocupada pelo mesmo pode ser reutilizada. Já o problema de fila cheia se modifica, pois como não há uma quantidade definida de memória alocada previamente, a fila pode crescer virtualmente sem limite.
Na prática, o crescimento é limitado pela memória disponível, mesmo assim, isso não se constitui em óbice significativo normalmente. Por essas razões, também não há necessidade de fazermos uma implementação circular e podemos manter o campo “prox” do último elemento sempre com o valor NULL.
Vamos verificar mais detalhadamente como ocorrem a inserção e a remoção. Quando a função “enfileirar” é chamada, ela recebe como parâmetro o novo elemento a ser inserido. Antes que ele possa ser colocado na fila, precisamos alocar o espaço de memória e guardar o endereço correspondente.
A fila será formada por uma lista de nós com apenas dois campos:
- Elemento – Que guarda o elemento a ser inserido na lista.
- Prox ‒ Que guarda o endereço do próximo nó.
Ao ser criado o nó, devemos fazer “prox” assumir valor nulo. Esse campo só se alterará quando um novo nó for inserido em seguida, caso em que “prox” guardará o valor do endereço desse nó. O nó criado será inserido quando o campo “prox” do nó anterior apontar para ele e o ponteiro “fim” for atualizado com o endereço do nó inserido.
A remoção é ainda mais simples. Basta fazer o ponteiro “inicio” avançar na fila, isto é, inicio = inicio -> prox. Em seguida, desalocamos o nó removido. O Código 15 mostra o enfileiramento e o Código 16 o desenfileiramento.
Código 15: Função enfileirar.
1 int enfileirar ( Elemento elemento ) {
2 No *novo_no = ( No * ) calloc ( 1 , sizeof ( No ) );
3 novo_no -> elemento = elemento;
4 novo_no -> prox = NULL;
5 if ( novo_no != NULL ) {
6 if ( fim != NULL )
7 fim->prox = novo_no;
8 else {
9 inicio = novo_no;
10 fim = novo_no;
11 return 1; //sucesso
12 } else
13 return 0; //falha
14 }
Olhando o Código 15, percebemos que a linha 5 verifica se houve sucesso na alocação de um novo nó. Se esse nó tiver sido alocado com sucesso, o programa segue para a linha 6, que verifica se a fila é vazia (pelo que explicamos antes, basta testar um dos ponteiros de controle). Se a fila não for vazia, a linha 7 faz o nó apontado pelo ponteiro “fim” apontar para o novo nó e a linha 10 avança o fim da fila para o nó inserido.
Observe que a linha 10 é executada mesmo se a fila for vazia, caso em que a linha 9 também o é. Isso corresponde à situação que vimos de uma fila com um único nó.
Código 16: Função desenfileirar.
1 Elemento desenfileirar ( void ) {
2 int elemento_recuperado;
3 No *aux = inicio;
4 if ( inicio != NULL ) {
5 inicio = inicio->prox;
6 if ( inicio == NULL )
7 fim = NULL;
8 elemento_recuperado = aux->elemento;
9 free ( aux );
10 return elemento_recuperado; //sucesso
11 } else
12 return NULL; //falha
13 }
A função desenfileirar, mostrada no Código 16, é igualmente simples. A linha 4 verifica se a fila é vazia, o que inviabiliza a remoção. Se houver algum elemento na fila, basta avançar-se o ponteiro de “inicio”, o que é feito na linha 5. A linha 6 verifica se a fila se tornou vazia. Se tiver se tornado, o ponteiro “fim” precisa ser ajustado como na linha 7. Finalmente, em 9, o espaço de memória é liberado. Para isso, um ponteiro auxiliar é utilizado.
Da mesma maneira que na alocação sequencial, as operações de inserção e remoção são executadas em um número constante de passos.
A essa altura, você deve ter compreendido que a limitação da execução de inserções e remoções em posições específicas é a responsável pela redução da complexidade, pois torna dispensável a busca nas listas.
Para encerrar, apresentaremos um algoritmo que se vale de filas para realizar a ordenação.
A ordenação é um problema frequentemente enfrentado em computação e o Algoritmo 5 mostrado em pseudocódigo realiza a ordenação de “n” chaves utilizando-se “m” filas, sendo as chaves números inteiros numa base “m” > 1. Ou seja, o número de filas usadas é igual à base usada na representação numérica das chaves. Isso significa que para ordenar chaves decimais, serão utilizadas 10 filas. Esse tipo de ordenação é chamado ordenação por distribuição. O processo todo é relativamente simples.
Para realizar a ordenação, a lista de entrada com as “n” chaves é percorrida. Nessa primeira passagem, é avaliado o dígito menos significativo. As filas auxiliares são Fi, com “i” variando de 0 até “m” – 1. Logo, para o caso decimal, temos que “i” varia de 0 até 9. Os dígitos menos significativos são comparados ao índice “i”. Quando forem iguais, a chave é inserida nessa fila.
Ao fim da passagem, as chaves estarão distribuídas pelas filas, segundo seu dígito menos significativo. Uma nova fila de entrada é, então, construída a partir da concatenação das filas, mantendo-se a ordem de seu índice. Isto é, F0 – F1 - ... – F9.
Uma segunda passagem é feita, tendo como entrada essa nova fila, empregando-se o mesmo princípio, mas agora comparando-se o segundo dígito mais significativo. O algoritmo terminará após a concatenação da última fila, construída a partir da distribuição feita considerando-se o dígito mais significativo.
Algoritmo 5: Ordenação por distribuição.
1 ordenacaoPorDistribuicao ( int m , int n , int Entrada [ ] )
2 int nr_digito = m - 1 , aux
3 int Fila [ nr_digito ]
4 para i = 0 até i < m - 1
5 para j = 0 até n - 1
6 aux = o i-ésimo digito menos significativo de Entrada [ j ]
7 Fila [ aux ] = Entrada [ j ]
8 j = 1
9 para aux = 0 até m - 1
10 enquanto Fila [ aux ] tiver elemento não processado
11 Entrada [ j ] = Fila [ aux ]
12 j++
APLICANDO FILAS
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Como vimos, estruturas de dados são elementos úteis e fundamentais na área de TI. Nessa oportunidade, nos detivemos em uma estrutura específica, que nos ajudou a compreender a manipulação de dados na memória do computador. Para isso, começamos entendendo os mecanismos de alocação sequencial e encadeada. Com base neles, firmamos as bases para desenvolver a teoria sobre listas lineares.
Após os mecanismos de alocação, compreendemos os conceitos de lista linear e as operações de inserção, busca e remoção. Entendemos a forma como tais operações se processam e as consequências que trazem para o desempenho dos programas que as utilizam. Pudemos comparar, também, como os diferentes mecanismos de alocação impactam na implementação das listas.
Em seguida, abordamos o primeiro caso particular de lista linear, a pilha. Trata-se de um caso mais simples, porém de grande utilidade, como pudemos ver, habilitando diversas funcionalidades usadas no nosso dia a dia. A pilha foi apresentada usando algoritmos escritos em linguagem C, com uma visão real de sua aplicação e não apenas um conceito teórico.
Depois, apresentamos a fila, outro caso particular de pilha, mas que compreende maior complexidade do que a pilha. No estudo da fila, olhamos os diferentes impactos que os mecanismos de alocação têm sobre sua implementação e visualizamos as suas operações através de implementações em linguagem C.
Finalmente, de maneira a consolidar o conhecimento desenvolvido, propusemos questões que buscaram explorar os conceitos mostrados e levar à extrapolação dos mesmos. As questões envolveram a forma como os conceitos se interconectam e os desdobramentos. Com isso, concluímos o aprendizado deste importante tema.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Reconheceu os principais conceitos envolvidos na manipulação de dados na memória
Contrastou a forma de manipulação por encadeamento da manipulação com estruturas sequenciais
Identificou os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de pilhas
Reconhecer os algoritmos das principais operações, baseados na linguagem C, e as características peculiares de filas.
