Descrição

A construção dos principais conceitos e aplicações fundamentais da Eletrostática para distribuições contínuas de cargas elétricas, Lei de Gauss e suas aplicações na moderna teoria eletrodinâmica clássica.

PROPÓSITO

Generalizar os conceitos e aplicações de campo elétrico e potencial elétrico para distribuições contínuas de cargas, por meio da Lei de Coulomb e da Lei de Gauss, com aplicações diretas na obtenção de potenciais elétricos e capacitâncias de sistemas eletrostáticos.

Preparação

Antes de iniciar o conteúdo deste tema, revise seus estudos nos princípios da Álgebra Vetorial e do Cálculo Diferencial e Integral. Também será útil ter em mãos uma calculadora científica.

OBJETIVOS

Módulo 1

Identificar o campo elétrico de cargas contínuas

Módulo 2

Aplicar a Lei de Gauss do campo elétrico

Módulo 3

Calcular o potencial elétrico de cargas contínuas

Módulo 4

Calcular a capacitância

Introdução

A Eletrodinâmica Clássica é a interação fundamental com que experimentamos e observamos a natureza do universo. Nossa ciência e tecnologia necessitam desses conhecimentos para continuar progredindo. Vamos generalizar e aprofundar o tema da Eletrostática para distribuições contínuas de cargas elétricas, compreender uma das leis fundamentais da natureza, a Lei de Gauss, e aplicar esses conhecimentos a alguns de seus subprodutos, o cálculo de potenciais elétricos e capacitâncias: o início da tecnologia elétrica. Bons estudos!

MÓDULO 1

Identificar o campo elétrico de cargas contínuas

Lei de Gauss e suas aplicações

Introdução

A Eletrostática não se limita ao estudo dos princípios e fenômenos de cargas e campos elétricos de distribuições discretas de cargas. Na verdade, podemos generalizar esses conceitos para fenômenos nos quais as cargas elétricas estão continuamente distribuídas, formando um continuum de cargas elétricas e seus campos. Certamente, as cargas elétricas são discretizadas, individuais, como sabemos da Física Microscópica, mas vamos considerar que tenhamos tantas cargas elétricas e tão próximas, umas das outras, que possamos considerá-las distribuídas continuamente.

Você sabia

Pense na circunstância de um fluido. Sabemos que um corpo fluídico é composto por moléculas que podem ser individualizadas, mas no conjunto formam uma substância fluídica.

Então, vamos utilizar essa aproximação e tratar de conjuntos contínuos de cargas elétricas, nos quais não mais individualizaremos as cargas elétricas de partículas, mas de corpos elétricos carregados por cargas elétricas distribuídas formando um continuum de cargas, isto é, distribuições contínuas de cargas elétricas e suas densidades de cargas, que já vamos definir.

Para distribuições de cargas elétricas discretas, definimos o campo eletrostático, por meio da Lei de Coulomb e do princípio de superposição, em que o campo resultante, medido em certo ponto P, é o somatório dos campos de cada carga fonte individualizada.

$\vec{E} (r) \equiv \frac{1}{4 π \in_{0}} \sum_{i = 1}^{n} \frac{q_{i}}{r_{i}^{2}} {\hat{r}}_{i}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Mas se as cargas elétricas formarem um continuum de cargas, precisaremos alterar nossa definição de campo elétrico, na qual substituiremos o somatório, que indica a discretização das cargas e posições destas, por uma integral, que indica um continuum de elementos de carga e funções contínuas de posição.

$\vec{E} (r) = \frac{1}{4 π \in_{0}} \int \frac{1}{r^{2}} \hat{r} d q$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Os elementos de carga elétrica, dq, são usualmente definidos em termos de densidades de cargas elétricas. Na equação acima, r indica a distância de cada elemento de carga dq ao ponto de medida do campo, e $\hat{r}$ é o vetor unitário direcional de cada elemento de carga ao mesmo ponto de medida do campo, não sendo, portanto, um vetor unitário constante, e assim devem ser considerados na integração.

Demonstração

Para demonstrar como se processa o cálculo do campo eletrostático para distribuições contínuas de cargas elétricas, precisamos demonstrar como definir o que são densidades de cargas elétricas e seu campo elétrico associado.

Densidades de cargas elétricas

Os materiais elétricos, ou eletrizáveis, podem conter cargas elétricas distribuídas de três formas distintas: linearmente, superficialmente ou volumetricamente. Essencialmente, será a relação da carga do material, em uma região delimitada do espaço com simetria linear, superficial ou volumétrica, com sua geometria.

Clique nas barras para ver as informações. Objeto com interação.

I - Densidade linear de cargas λ :

$d q = λ d l \to λ = \frac{d q}{d l}$

II - Densidade superficial de cargas σ:

$d q = σ d A \to σ = \frac{d q}{d A}$

III - Densidade volumétrica de cargas
ρ:

$d q = ρ d V \to ρ = \frac{d q}{d V}$

Em que dl é o elemento de comprimento ao longo de uma linha, dA é o elemento de área de uma superfície e dV é o elemento de volume.

Assim, sempre que tivermos um material carregado num continuum de cargas, para cada simetria de um problema e sua densidade de cargas, teremos uma configuração do campo eletrostático. Devemos atentar para o fato de que as cargas são estáticas e conservadas, ou seja, dizemos que a totalidade das cargas elétricas com que lidamos na Eletrostática é estacionária.

Campo eletrostático para distribuições contínuas de cargas elétricas (Lei de Coulomb)

Clique nas barras para ver as informações. Objeto com interação.

\vec{E} (r)

para distribuições lineares de cargas:

\vec{E} (r)

para distribuições superficiais de cargas:

\vec{E} (r)

para distribuições volumétricas de cargas:

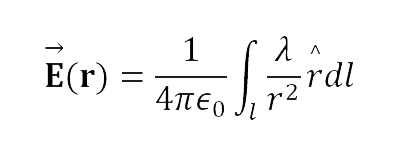
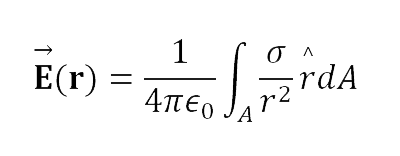
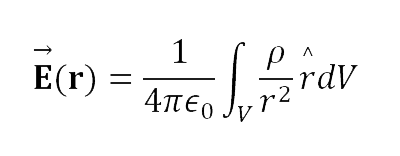
Ainda vamos definir os conceitos de materiais condutores.

Comentário

Os materiais carregados podem possuir diferentes densidades de cargas em suas geometrias, definidas por regiões de carga, mas para este tema, vamos aplicar a problemas com densidades de cargas constantes ou de funções simples.

Em quaisquer das situações de simetrias e geometrias, é usualmente conveniente trabalhar com elementos de campo elétrico e, ao final, integrá-los para o campo resultante:

$\vec{E} (r) = \int d \vec{E}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Mão na Massa

Teoria na prática

Aplicação: Uma das importantes aplicações práticas da Eletrostática diz respeito a esse problema. Considere uma casca esférica, oca, homogênea, de raio R, e superficialmente carregada com uma densidade superficial de cargas, σ, constante. Calcule, via Lei de Coulomb, o seu campo elétrico interno à casca, com $r < R .$

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Já fizemos um problema semelhante, porém para o cálculo do campo externo à casca esférica. Todos os passos são idênticos, até antes da integração final. Retomemos aquele resultado. Vamos, então, posicionar o ponto P dentro da casca e alterar os limites de integração em S para esses pontos internos à casca, de $(R - r) a (R + r) .$

Etapa 1

$d E_{r} (p) = \frac{k σ π R}{r^{2}} [1 + \frac{r^{2} - R^{2}}{S^{2}}] d S$

$E_{r} (p) = \int d E_{r}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Etapa 2

$E_{r} (p) = \frac{k σ π R}{r^{2}} {[S - \frac{(r^{2} - R^{2})}{S}]}_{(R - r)}^{(R + r)}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Etapa 3

$E_{r} (p) = \frac{k σ π R}{r^{2}} [(R + r) - (R - r) - \frac{(r^{2} - R^{2})}{(R + r)} + \frac{(r^{2} - R^{2})}{(R - r)}]$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Etapa 4

$E_{r} (p) = \frac{k σ π R}{r^{2}} [2 r - r + R - r - R] = 0$

$\vec{E} (p) = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O campo elétrico interno a uma superfície esférica, oca e homogeneamente carregada é nulo. Esse fenômeno de blindagem eletrostática, muito utilizado tecnologicamente, tem o nome de Gaiola de Faraday. Perturbações elétricas externas à casca fechada não afetam o campo elétrico interno à casca, que continua nulo.

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 2

Aplicar a Lei de Gauss do campo elétrico

Introdução

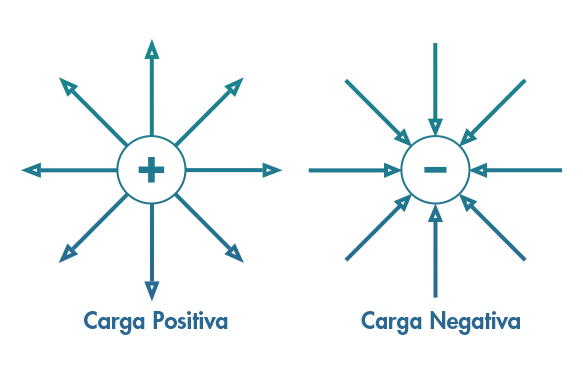
Sabemos que cargas elétricas, numa distribuição discreta ou contínua, são fonte de campo elétrico mediador da interação elétrica. Também sabemos que os campos elétricos podem ser representados por linhas de força que “nascem ou morrem” em cargas. Usamos uma convenção na qual cargas positivas originam linhas de campo repulsivo e cargas negativas recebem linhas de campo atrativo:

Para cada distribuição de cargas elétricas, teremos uma estrutura de campo elétrico diferente. Cargas puntuais geram uma estrutura de campo elétrico divergente, como nas figuras anteriores. Para outras distribuições de cargas, teremos outras estruturas de campo elétrico. Quanto maior a carga, mais linhas de campo teremos, (N ~ q).

O campo elétrico de cargas puntuais e sua força elétrica se comportam radialmente como ~ 1/r², descrito pela Lei de Coulomb. A magnitude do campo (seu módulo) é proporcional à densidade de linhas, que é o número de linhas de campo por área perpendicular atravessada pelas linhas, $(δ ~ \frac{N}{A} ~ \frac{q}{4 π r^{2}} ~ |\vec{E}|) .$ .

Quanto maior essa densidade, onde as linhas são mais próximas, mais intenso o campo. Quanto menor a densidade de linhas, menos intenso o campo. À medida que nos afastamos das cargas puntuais, as linhas de campo se distanciam, umas das outras, diminuindo sua densidade com o mesmo comportamento coulombiano do campo, e na proporção inversa do crescimento da área esferossimétrica ocupada por essas linhas.

Então, vamos enumerar o que sabemos sobre linhas de campo elétrico:

O número de linhas de campo elétrico é proporcional à carga elétrica, (N ~ q).
As linhas de campo elétrico de cargas puntuais isoladas são radialmente simétricas, a cada raio esférico ocupando áreas descritas por A=4πr ².
As linhas de campo são emitidas ou absorvidas por cargas elétricas.
A densidade de linhas é proporcional à magnitude do campo, $(δ ~ \frac{N}{A} ~ \frac{q}{4 π r^{2}} ~ |\vec{E}|)$ .
Duas ou mais linhas não se interceptam, o que indicaria que uma mesma linha teria mais de uma fonte.

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Assim, determinado número de linhas de campo elétrico, em uma distância radial esférica, atravessará certa calota de área na superfície esférica de mesmo raio, em um ângulo sólido. O mesmo número de linhas de campo, em outro raio esférico maior, atravessará uma calota da superfície esférica, com o mesmo ângulo sólido, de área proporcional ao quadrado do novo raio. Isso significa que, para termos o mesmo número de linhas, em raios diferentes, cuja magnitude do campo cai com o quadrado do raio, será preciso aumentar a área de ocupação dessas linhas com o quadrado do novo raio. O comportamento do campo $(~ \frac{1}{r^{2}})$ , será anulado pelo crescimento da área $(~ r^{2})$ , para termos o mesmo número de linhas de campo elétrico em raios diferentes, como na figura.

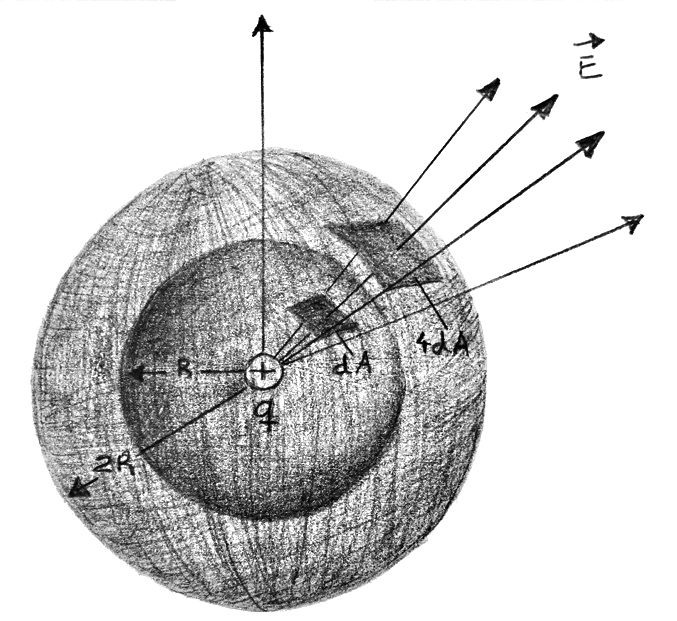
Fluxo de campo elétrico

Vamos qualificar e quantificar as linhas de campo elétrico em termos matemáticos com significação fenomenológica. Para isso, vamos definir a grandeza fluxo de campo elétrico, $Φ$ , como proporcional ao número de linhas de campo, que é proporcional à carga elétrica. Assim, o fluxo de campo será:

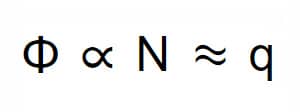
Mas,

N ~ |\vec{E}| A

Pois, como explicado anteriormente sobre as linhas de campo,
$δ ~ \frac{N}{A} ~ \frac{q}{4 {πr}^{2}} ~ |\vec{E}|$

Então, $Φ = | \vec{E} | A \approx q$

O fluxo de campo é entendido como o número de linhas de campo elétrico que atravessam a superfície de área A.

Essa definição de fluxo de campo elétrico funciona bem para o caso de campos elétricos, $\vec{E}$ , que atravessam perpendicularmente uma área, A, como na figura a), a seguir.

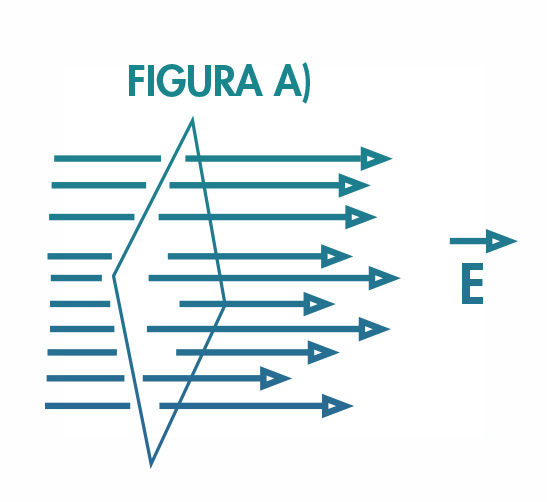
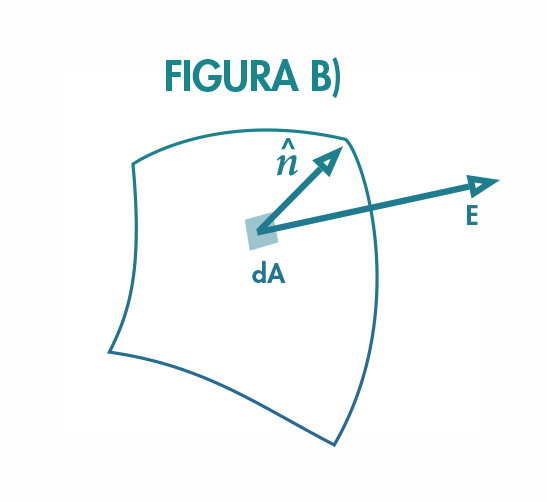
Repare que essa primeira definição de Fluxo de Campo, não satisfaz a situação da figura b), anterior, do fluxo através de uma superfície curva, em que para cada elemento de área, dA, descrito sobre a superfície em cada ponto, tem-se um vetor unitário normal diferente, $\hat{n}$ . Assim, devemos redefinir o fluxo de campo como a integral dos elementos de fluxo de campo, $dΦ$ , definidos sobre cada elemento de área, dA, com seu vetor unitário normal, $\hat{n}$ , por meio do produto escalar com o campo $\vec{E}$ . Contribuirá ao fluxo, a componente de área ( $\hat{n}$ dA) projetada na direção do campo $\vec{E}$ .

$d Φ = \vec{E} . \hat{n} d A$
$Φ = \int d Φ = \int \vec{E} . \hat{n} d A$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como o fluxo de campo elétrico através de qualquer superfície aberta é igual ao número de linhas de campo que atravessam essa superfície, podemos definir o fluxo total que será igual ao número líquido de linhas de campo elétrico que atravessam a superfície fechada, isto é, o número de linhas que saem subtraído do número de linhas que entram na superfície fechada.

O fluxo total será a soma “líquida” do fluxo positivo, com campo $\vec{E}$ orientado para fora da superfície fechada, subtraído do fluxo negativo, com campo $\vec{E}$ orientado para dentro da superfície fechada:

$Φ_{t o t a l} = \oint_{c}^{} d Φ = \oint_{c}^{} \vec{E} . \hat{n} d A$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que c, define a superfície matemática sobre a qual a integral deve ser calculada, chamada de superfície gaussiana e $\hat{n}$ é o vetor normal a cada ponto dessa gaussiana.

Mas para que serve essa construção do fluxo de campo elétrico total? A resposta é a Lei de Gauss e a sua aplicação imediata é o cálculo do campo elétrico.

Demonstração

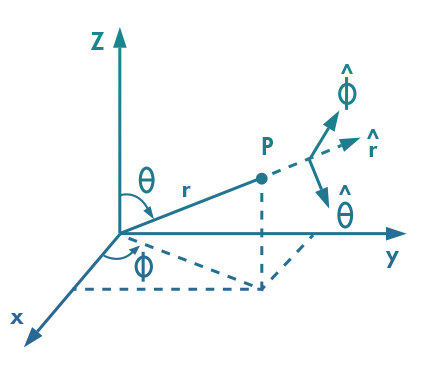
Aplicação: Uma carga elétrica puntual, q, fonte do campo elétrico descrito pela Lei de Coulomb, $\vec{E} = \frac{1}{4 {πϵ}_{0}} \frac{q}{r^{2}} \hat{r}$ , está na origem de um sistema coordenado. Calcule o fluxo de campo elétrico total sobre uma superfície matemática esférica fechada de raio R, centrada na mesma origem. Considere a medida de integração de superfície, dA, em coordenadas esféricas $(r, θ, ϕ) : d A = r^{2} s e n θ d θ d ϕ$ .

Resposta 1:

Escolha uma das Etapas a seguir.

ETAPA 1

ETAPA 2

ETAPA 3

Nesta primeira solução, mais simples, vamos considerar que, como o fluxo será calculado ao longo da superfície gaussiana esférica de raio R, seu campo elétrico terá módulo constante, com r=R, o vetor unitário normal à superfície esférica será $\hat{n} = \hat{r}$ , e o campo $\vec{E} = \frac{1}{4 π ϵ_{0}} \frac{q}{R^{2}} \hat{r}$ .

Então, como $(\hat{r} . \hat{n}) = 1$ , pois o vetor unitário $\hat{n}$ tem a mesma direção e sentido de $\hat{r}$ , e o raio da superfície esférica de cálculo (gaussiana), sobre a qual se está calculando o fluxo, é constante, $r = R$ , temos:

$Φ_{t o t a l} = \oint_{c}^{} \vec{E} . \hat{n} d A = \oint_{c}^{} \frac{1}{4 π ϵ_{0}} \frac{q}{R^{2}} (\hat{r} . \hat{n}) d A$

$Φ_{t o t a l} = \oint_{c}^{} \frac{1}{4 π ϵ_{0}} \frac{q}{R^{2}} d A = \frac{1}{4 π ϵ_{0}} \frac{q}{R^{2}} \oint_{c}^{} d A$

$Φ_{t o t a l} = \frac{1}{4 π ϵ_{0}} \frac{q}{R^{2}} 4 π R^{2} = \frac{q}{ϵ_{0}} = 4 π k q$

Este é o resultado da Lei de Gauss. O fluxo de campo elétrico total $Φ_{t o t a l} = \frac{q}{ϵ_{0}} = 4 π k q$ , independente do raio r. O número de linhas de campo elétrico será o mesmo para qualquer raio esférico. Na verdade, apesar de não ter sido demonstrado, o fluxo total é o mesmo qualquer que seja a superfície fechada que envolva a carga q, não se limitando à esfera.

Resposta 2:

Escolha uma das Etapas a seguir.

ETAPA 1

ETAPA 2

ETAPA 3

Nesta segunda solução, vamos calcular a integral do fluxo total com medida de integração de superfície, em coordenadas esféricas, $d A = r^{2} s e n θ d θ d ϕ$ , para qualquer raio da superfície esférica de integração.

$Φ_{t o t a l} = \oint_{c}^{} \vec{E} . \hat{n} d A = \oint_{c}^{} \frac{1}{4 π ϵ_{0}} \frac{q}{r^{2}} (\hat{r} . \hat{r}) d A$

$Φ_{t o t a l} = \oint_{c}^{} \frac{1}{4 π ϵ_{0}} \frac{q}{r^{2}} r^{2} s e n θ d θ d ϕ$

Φ_{t o t a l} = \frac{1}{4 π ϵ_{0}} q \int_{0}^{π} s e n θ d θ \int_{0}^{2 π} d ϕ

Em que

$(0 < θ < π); (0 < ϕ < 2 π); \int_{0}^{π} s e n θ d θ = [- \cos (π) + \cos (0)] = 2; \int_{0}^{2 π} d ϕ = 2 π$

Logo,

$Φ_{t o t a l} = \frac{1}{4 π ϵ_{0}} q 4 π = \frac{q}{ϵ_{0}} = 4 π k q$

Assim, definimos a Lei de Gauss:

$Φ_{t o t a l} = \oint_{c}^{} \vec{E} . \hat{n} d A = \frac{q_{i n t .}}{ϵ_{0}} = 4 π k q_{i n t .}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que q_int. é a carga elétrica total interna à superfície gaussiana c, de integração.

A Lei de Gauss é uma das leis fundamentais da Eletrodinâmica Clássica, será sempre válida quando houver campo elétrico, mas, para o propósito de cálculo do campo elétrico, somente será útil quando tivermos elevado grau de simetria no problema, para a escolha da superfície gaussiana, de forma que o módulo do campo seja constante ao longo dessa superfície de integração.

De outra forma, se um sistema físico não tiver as simetrias esférica, cilíndrica ou plana, será mais simples a utilização da Lei de Coulomb e seus métodos quando o propósito for o cálculo do campo. Esse resultado da Lei de Gauss, no qual o fluxo de campo total só depende da fonte do campo, só foi possível devido ao comportamento da Lei de Coulomb, com 1/r².

Assim, também por similaridade de comportamento 1/r², podemos escrever uma Lei de Gauss para a Gravitação Universal de Newton, em que:

$Φ_{t o t a l} = \oint_{c}^{} \vec{g} . \hat{n} d A = - 4 π G m_{i n t .} s e n d o m_{i n t .}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo m_int. a massa interna à superfície gaussiana c.

Mão na Massa

Teoria na prática

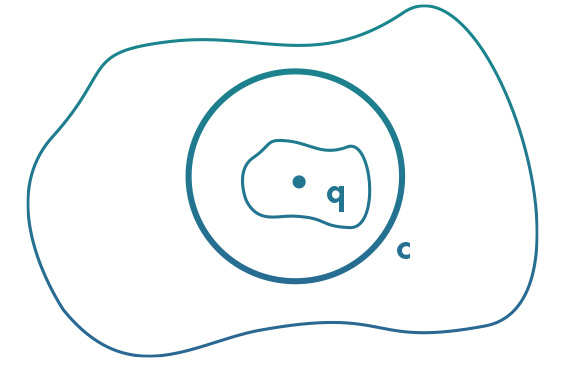
Aplicação: Um condutor ideal maciço tem uma cavidade oca em seu interior, como uma bolha. Uma pequena carga elétrica q foi suspensa, por um fio não condutor, no interior dessa cavidade oca, sem que a carga toque as paredes da cavidade. Pergunta-se: Qual a carga elétrica induzida na superfície interna das paredes da cavidade?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

CAMPO DE INDUÇÃO ELETROSTÁTICO

$ϕ_{t o t} = \oint_{c} \vec{E} \cdot \hat{n} d A = 4 π k {q_{i n t}}_{c}$

A superfície C que envolve a cavidade é a superfície gaussiana. Como no interior de um condutor ideal o campo elétrico deve ser nulo, o fluxo total de campo sobre C será zero e a carga total interna a C deve ser zero. Se há uma carga q, no interior da cavidade, necessariamente haverá uma densidade de cargas induzidas eletrostaticamente nas paredes internas da cavidade. Esse é o mecanismo da eletrização por indução eletrostática. Assim, a carga induzida será:

$Q = q + q^{'} = 0 \to q^{'} = - q$ .

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 3

Calcular o potencial elétrico de cargas contínuas

Introdução

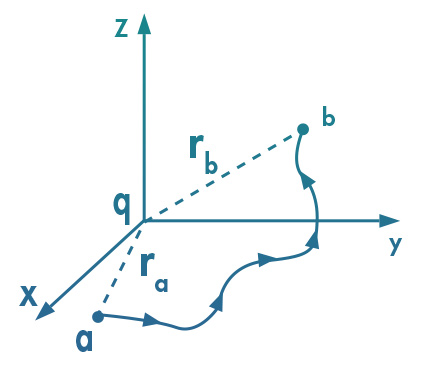
Sabemos, do tema anterior, que a diferença de potencial elétrico é definida como:

$∆ V = V_{b} - V_{a} = - \int_{a}^{b} \vec{E} . d \vec{l}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que, no caso eletrostático, o trabalho mecânico numa trajetória fechada será nulo, o que equivale à integral acima ser zero quando a = b.

$\oint \vec{E} . d \vec{l} = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Isso é válido para campos conservativos, como os campos eletrostáticos. Em termos do potencial elétrico, a diferença de potencial entre um ponto e ele mesmo, numa trajetória fechada, será zero.

Então, relembrando a definição conceitual do potencial elétrico, em sua forma integral, temos:

Potencial elétrico é o trabalho por unidade de carga, necessário para deslocar uma carga de prova positiva, à velocidade constante, de um ponto de referência inicial a ao ponto final r, definido por:

$V (r) = - \int_{a}^{r} \vec{E} . d \vec{l}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo a um ponto de referência espacial onde V(a)=0. O potencial será positivo ou negativo a depender da distribuição de cargas fonte do campo.

Também podemos relembrar a definição equivalente na forma diferencial do potencial elétrico, que é muito útil quando temos a função potencial e desejamos calcular o campo elétrico. O campo elétrico como o gradiente da função potencial.

$\vec{E} = - \vec{\nabla} V (r)$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como o que nos interessa na grandeza potencial elétrico é uma diferença a partir de uma referência de medida de zero potencial, V(a)=0, a cada problema deveremos identificar, ou convencionar, a referência de potencial zero, já que vamos lidar com distribuições contínuas de cargas elétricas. Nessas configurações contínuas de cargas, nem sempre a distância infinita será consistente com um potencial nulo de referência, como é suficiente para distribuições discretas de cargas.

Nossa tarefa, agora, será demonstrar como aplicar o conceito e as definições de potencial elétrico para distribuições contínuas de cargas elétricas.

Demonstração

Quando lidamos, no tema anterior, com configurações discretas de cargas elétricas, vimos que o cálculo do potencial elétrico poderia ser realizado por meio da definição do potencial, nas formas integral ou diferencial, revisitado nas duas equações anteriores, e demonstramos que poderíamos usar o princípio de superposição dos potenciais de cargas individuais para descrever o potencial de uma distribuição discreta de cargas elétricas, pela soma dos potenciais de cargas individualizadas:

$V (p) = V_{1} + V_{2} + V_{3} + \dots V_{N} = \sum_{i = 1}^{N} k \frac{q_{i}}{r_{i}}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Com N cargas q_i e distâncias r_i de cada carga fonte ao ponto de medida p. Assim, o potencial elétrico total de uma distribuição discreta de cargas elétricas será a superposição dos potenciais individuais de cada fonte q_i (princípio de superposição).

No entanto, para distribuições contínuas de cargas elétricas, devemos identificar se a configuração de cargas é finita ou infinita.

Se for uma distribuição contínua e finita de cargas elétricas, pois o número de cargas é finito, como nos problemas da esfera, do anel e do disco, visto do módulo anterior, o potencial elétrico poderá ser definido e calculado por uma generalização da superposição de potenciais individuais, da equação anterior.

Assim, o potencial elétrico para configurações contínuas e finitas de cargas elétricas é:

$V (p) = \int \frac{k d q}{r}$

Que é a integral de todas as contribuições de potenciais dos elementos dq, no intervalo a ser considerado.

Se a distribuição de cargas elétricas for contínua e infinita, como nos casos da reta infinita, do plano infinito e do cilindro infinito, o potencial elétrico para distribuições contínuas e infinitas de cargas elétricas segue a definição formal de cálculo dos potenciais elétricos, que, aliás, aplica-se em qualquer situação de configurações de cargas.

$V (r) = - \int_{a}^{r} \vec{E} . d \vec{l} o u \vec{E} = - \vec{\nabla} V (r)$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Ou seja, a depender da configuração das cargas fonte do campo $\vec{E}$ , se discretas ou contínuas, e se forem contínuas, se finitas ou infinitas, teremos os seguintes métodos de cálculo do potencial elétrico:

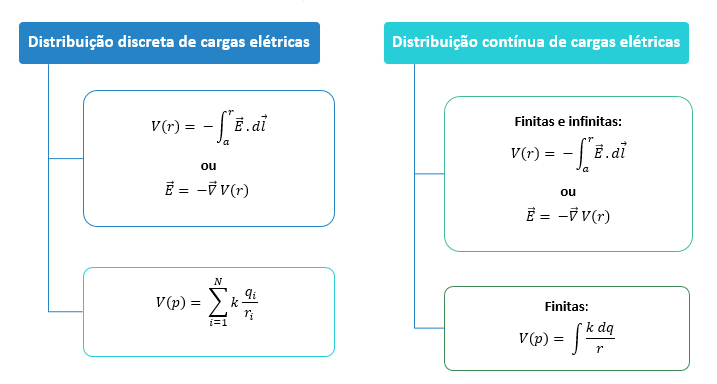
Agora, vamos à prática!

Mão na Massa

Teoria na prática

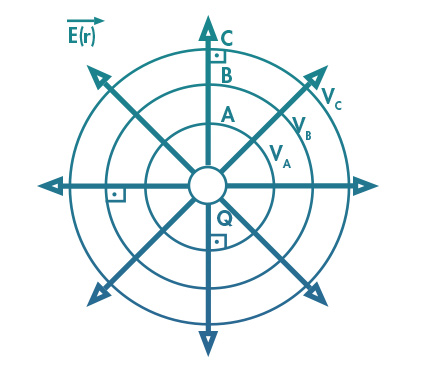
Considere uma esfera, de raio R e carga total Q, geradora de um potencial elétrico esfericamente simétrico. A cada distância radial esférica, podemos traçar uma superfície esférica, de raio r, onde o potencial elétrico será o mesmo ao longo de toda essa superfície. Para cada outra superfície equivalente, de outro raio, centrada na origem, teremos uma superfície de potencial constante. Pergunta-se: Como é possível ter superfícies de mesmo potencial elétrico e qual a sua utilidade?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Escolha uma das Etapas a seguir.

ETAPA 1

ETAPA 2

ETAPA 3

As superfícies de mesmo potencial elétrico, chamam-se superfícies equipotenciais. São aquelas nas quais uma carga de prova pode mover-se livremente sem alteração de seu potencial elétrico.

No caso esférico, o potencial será $V (r) = \frac{k Q}{r}$ , e para cada raio esférico, teremos uma superfície equipotencial naquele raio, $V_{A}, V_{B}, V_{C}, \dots .$ As linhas de campo elétrico $\vec{E}$ serão perpendiculares às superfícies equipotenciais.

Como cargas elétricas somente são aceleradas na presença de diferenças de potencial elétrico, em superfícies equipotenciais isso não ocorre. E assim, nenhum pássaro morre quando pousa em uma única linha de tensão elétrica, por exemplo.

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 4

Calcular a capacitância

Capacitância

Chamamos de capacitância a habilidade de acumulação de cargas elétricas e energia elétrica por componentes elétricos ou sistemas elétricos, diante de diferenças de potencial elétrico.

É um fenômeno natural, que pode ser identificado na natureza, entre as nuvens e o solo, em materiais que acumularam cargas estáticas e sua vizinhança física, em sistemas elétricos e eletrônicos, sendo macroscópicos ou microscópicos (em eletrônica em grande escala de integração). Em termos práticos, nosso interesse está na possibilidade de utilização tecnológica dessa energia armazenada.

Figura: Imagem Ilustrativa para Capacitância

Certamente, ao ler estas linhas, seu equipamento computador, ou mídia eletrônica, possui alguns bilhões de capacitores em seus circuitos integrados microscopicamente. Atualmente, convivemos com acumuladores elétricos de energia a todo instante: baterias, pilhas, capacitores etc. Essencialmente, todos têm a capacidade de acumular energia em forma elétrica.

Comentário

A simples habilidade dos materiais de acumular cargas elétricas pode transformar esse sistema em um rudimentar capacitor, e essa habilidade pode ser mensurada por sua capacitância.

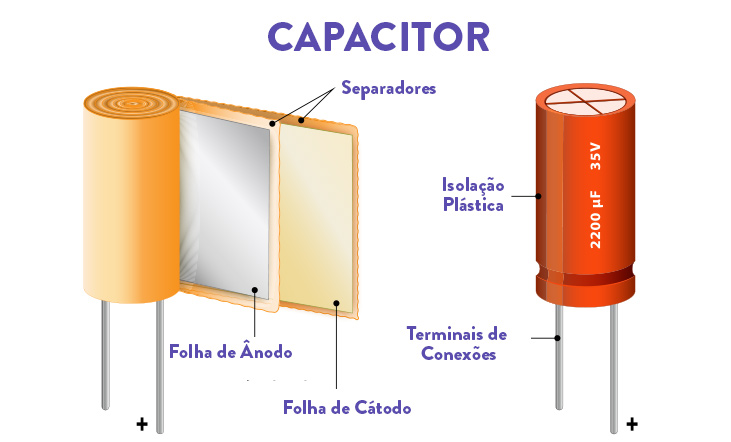
Vamos nos limitar aqui aos componentes acumuladores de energia que costumamos chamar de capacitores. A ideia essencial de um capacitor é de um componente elétrico, ou eletrônico, composto por duas paredes condutoras separadas mecanicamente por um material dielétrico, um não condutor ideal. Vamos deixar o aprofundamento sobre os dielétricos para o Explore+.

Por ora, vamos pensar no desenho básico de um capacitor: duas placas condutoras, dispostas paralelamente, bem próximas, mas separadas por uma distância d. Esses componentes são essenciais à eletrônica e à elétrica em geral. Certamente, você já ouviu falar da necessidade de correção de instalações elétricas, em indústrias, com o ajuste necessário de um banco de capacitores. Bem, isso também ficará para mais tarde. O importante é compreender que o fenômeno da capacitância é parte da nossa experiência natural e tecnológica.

Vamos definir capacitância como a constante de proporcionalidade, de unidade S.I. Faraday (F), entre as cargas elétricas acumuladas nas paredes de um capacitor e a diferença de potencial elétrico necessária para produzir esse acúmulo:

$C = \frac{Q}{|∆ V|}$

Se um capacitor, em um circuito elétrico, for alimentado com uma diferença de potencial elétrico ∆V, por uma fonte de tensão elétrica e, consequentemente, acumular cargas elétricas, Q, em suas paredes, de tal maneira a estabelecer a mesma diferença de potencial na região entre essas paredes, o acúmulo de cargas cessará e o capacitor estará carregado eletricamente.

Demonstração

Os capacitores podem ser conectados em arranjos de capacitores em série e em paralelo. Sempre que conectarmos capacitores, em combinações em série e em paralelo, o resultado será o de uma capacitância equivalente. Se precisarmos, como exemplo, de um capacitor de determinado valor de capacitância, podemos combinar outros capacitores de forma a obter a capacitância equivalente desejada.

Atenção

Não confunda capacitores (componentes) com capacitância (fenômeno)!

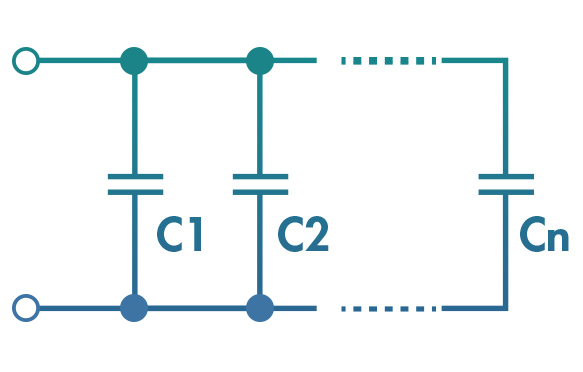
Arranjo em Paralelo

Vamos considerar a combinação de N capacitores em paralelo, como na figura. Perceba que a carga total acumulada no sistema de capacitores será a soma das cargas de cada capacitor C_i, em que $i = 1, 2, 3, \dots, N$ . Ou seja, $Q_{total} = \sum_{i = 1}^{N} Q_{i}$ .

Nesse arranjo, em paralelo, cada capacitor será alimentado com a mesma diferença de potencial ∆V. Então, a capacitância equivalente C_eqem paralelo será:

$\begin{matrix} Q_{total} = Q_{1} + Q_{2} + \dots + Q_{N} \\ ΔV \cdot C_{eq} = ΔV (C_{1} + C_{2} + \dots + C_{N}) \\ C_{eq} = \sum_{i = 1}^{N} C_{i} \end{matrix}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

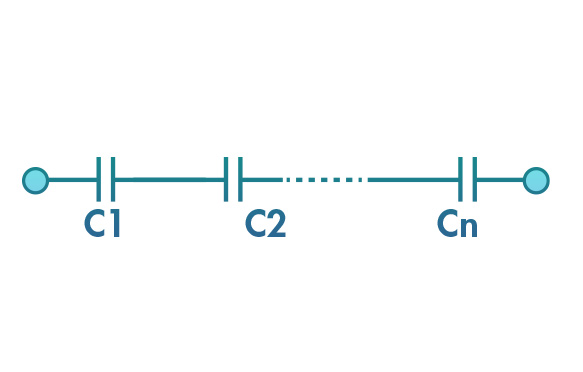
Arranjo em Série

Vamos considerar, agora, a combinação de N capacitores em série, como na figura. A diferença de potencial ∆V será a soma dos potenciais que alimentam cada capacitor $∆ V = \sum_{i = 1}^{N} V_{i} .$

Nesse caso, como cada capacitor acumulará a mesma carga elétrica, Q, em suas paredes, pois estão em série, a capacitância equivalente em série será:

$\begin{matrix} Δ V = V_{1} + V_{2} + \dots + V_{N} \\ \frac{Q}{C_{e q}} = \frac{Q}{C_{1}} + \frac{Q}{C_{2}} + \dots + \frac{Q}{C_{N}} \\ \frac{1}{C_{e q}} = \sum_{i = 1}^{N} \frac{1}{C_{i}} \end{matrix}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Vamos à prática!

Mão na Massa

Teoria na prática

Vamos pensar no processo de carga de um capacitor, cuja capacitância é definida linearmente pela definição padrão, $C = \frac{Q}{| ∆ V |}$ . Consideremos que esse capacitor seja alimentado com uma diferença de potencial $V_{0}$ entre suas paredes. Suponha, ainda, que possa acumular uma carga total Q, sendo (+ Q) numa parede e (–Q) na outra. Vamos definir o potencial zero na parede negativa e o potencial $V_{0}$ na parede positiva. Pergunta-se: Qual a é energia potencial elétrica, total, acumulada nesse capacitor?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Escolha uma das Etapas a seguir.

Etapa 01

A energia potencial elétrica é o potencial elétrico multiplicado pela carga de prova. Mas o capacitor em carga, não apresenta o potencial elétrico V₀ desde o início do processo de carga. O capacitor, na verdade, vai se carregando desde o potencial zero até o potencial V₀. As cargas elétricas vão se acumulando desde a carga zero, até a carga total Q. Assim, devemos integrar a energia potencial desde a carga zero até a carga máxima Q.

Etapa 02

$C = \frac{Q}{| Δ V |}$

$Δ V = V_{0}$

$V = \frac{q}{C}$

$d U = V d q$

Etapa 03

$Δ U = \int_{0}^{Q} V d q$

$Δ U = \int_{0}^{Q} \frac{q}{C} d q$

$Δ U = \frac{1}{2} \frac{Q^{2}}{C} = \frac{1}{2} C V_{0}^{2}$

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

Conclusão

Considerações Finais

A compreensão da teoria eletromagnética e seus fenômenos pressupõe a continuação dos estudos dos conceitos e fenômenos da Eletrostática, para distribuições contínuas de cargas elétricas e suas relações, como parte fundamental do que compreendemos hoje como a Teoria Eletrodinâmica Clássica.

Esses conceitos são a base de toda a nossa tecnologia e experiência contemporânea. Neste tema, você estudou os fenômenos, conceitos e definições de distribuições contínuas de cargas, seus campos, potenciais elétricos, o importantíssimo conceito de fluxo de campo, Lei de Gauss e aplicações à capacitância. Não deixe de experimentar as indicações complementares no Explore +.

Podcast

CONQUISTAS

Você atingiu os seguintes objetivos:

Identificou o campo elétrico de cargas contínuas

Aplicou a Lei de Gauss do campo elétrico

Calculou o potencial elétrico de cargas contínuas

Calculou a capacitância

Referências

BARROS, L. M. Física Teórica Experimental III. 1. ed. Rio de Janeiro: SESES, 2017.

GRIFFITHS, D. J. Eletrodinâmica. 3. ed. São Paulo: Pearson, 2019.

HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física: Eletromagnetismo. 10. ed. Rio de Janeiro: LTC, 2018. v. 3.

NUSSENZVEIG, H. M. Curso de Física Básica: Eletromagnetismo. 1. ed. digital. São Paulo: Blucher, 2018.

TIPLER, P. A. Física para Cientistas e Engenheiros. 6. ed. Rio de Janeiro: LTC, 2011.

YOUNG, H. D.; FREEDMAN, R. A. Física III – Sears & Zemansky. 14. ed. São Paulo: Addison Wesley, 2015. v. 3.

Explore+

Para saber mais sobre os assuntos tratados neste tema, leia:

Leia: Capacitância e Dielétricos

URL: http://fma.if.usp.br/~mlima/teaching/4320292_2012/Cap4.pdf

Experimente: Simulador de Hockey Elétrico

URL: https://phet.colorado.edu/en/simulation/legacy/electric-hockey

Experimente: Simulador John-travoltage

URL: https://phet.colorado.edu/en/simulation/john-travoltage

Experimente: Simulador de Capacitores

URL: https://phet.colorado.edu/en/simulation/legacy/capacitor-lab

Conteudista

Gentil Oliveira Pires

Currículo Lattes

Descrição

PROPÓSITO

Preparação

OBJETIVOS

Módulo 1

Módulo 2

Módulo 3

Módulo 4

Introdução

MÓDULO 1

Lei de Gauss e suas aplicações

Introdução

Você sabia

E→r≡14π∈0∑i=1nqiri2r^i

Discretização

E→r=14π∈0∫1r2r^dq

Demonstração

Densidades de cargas elétricas

Campo eletrostático para distribuições contínuas de cargas elétricas (Lei de Coulomb)

Comentário

E→r =∫dE→

Mão na Massa

Teoria na prática

dErp=kσπRr21+r2-R2S2dS

Er(p)=∫dEr

Erp=kσπRr2S-(r2-R2)S(R-r)(R+r)

Erp=kσπRr2R+r-R-r-r2-R2R+r+r2-R2R-r

Erp=kσπRr22r-r+R-r-R=0

E→p=0

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

Você chegou ao final do módulo 1!

MÓDULO 2

Introdução

Fluxo de campo elétrico

dΦ= E→.n^ dA Φ=∫dΦ=∫E→.n^ dA

Superfície fechada

Φtotal=∮c dΦ= ∮c E→.n^ dA

Demonstração

Φtotal= ∮c E→.n^ dA=qint.ϵ0=4π k qint.

Superfície gaussiana c

Φtotal= ∮c g→.n^ dA=-4π G mint. sendo mint.

Mão na Massa

Teoria na prática

CAMPO DE INDUÇÃO ELETROSTÁTICO

ϕtot=∮cE→⋅n^dA=4πk qintc

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

Você chegou ao final do módulo 2!

MÓDULO 3

Introdução

∆V= Vb-Va= -∫abE→. dl→

∮E→. dl→=0

Vr= -∫arE→. dl→

E→= -∇→ Vr

Demonstração

Vp=V1+ V2+V3+…VN= ∑i=1Nk qiri

Vr= -∫arE→. dl→ ou E→= -∇→ Vr

Mão na Massa

Teoria na prática

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

Você chegou ao final do módulo 3!

MÓDULO 4

Capacitância

Comentário

Demonstração

Atenção

Arranjo em Paralelo

Qtotal=Q1+Q2+⋯+QNΔV⋅Ceq=ΔV(C1+C2+⋯+CN)Ceq=∑i=1NCi

Arranjo em Série

ΔV=V1+V2+⋯+VNQCeq=QC1+QC2+⋯+QCN1Ceq=∑i=1N1Ci

Mão na Massa

Teoria na prática

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

$\vec{E} (r) \equiv \frac{1}{4 π \in_{0}} \sum_{i = 1}^{n} \frac{q_{i}}{r_{i}^{2}} {\hat{r}}_{i}$

$\vec{E} (r) = \frac{1}{4 π \in_{0}} \int \frac{1}{r^{2}} \hat{r} d q$

$\vec{E} (r) = \int d \vec{E}$

$d E_{r} (p) = \frac{k σ π R}{r^{2}} [1 + \frac{r^{2} - R^{2}}{S^{2}}] d S$

$E_{r} (p) = \int d E_{r}$

$E_{r} (p) = \frac{k σ π R}{r^{2}} {[S - \frac{(r^{2} - R^{2})}{S}]}_{(R - r)}^{(R + r)}$

$E_{r} (p) = \frac{k σ π R}{r^{2}} [(R + r) - (R - r) - \frac{(r^{2} - R^{2})}{(R + r)} + \frac{(r^{2} - R^{2})}{(R - r)}]$

$E_{r} (p) = \frac{k σ π R}{r^{2}} [2 r - r + R - r - R] = 0$

$\vec{E} (p) = 0$

$d Φ = \vec{E} . \hat{n} d A$
$Φ = \int d Φ = \int \vec{E} . \hat{n} d A$

$Φ_{t o t a l} = \oint_{c}^{} d Φ = \oint_{c}^{} \vec{E} . \hat{n} d A$

$Φ_{t o t a l} = \oint_{c}^{} \vec{E} . \hat{n} d A = \frac{q_{i n t .}}{ϵ_{0}} = 4 π k q_{i n t .}$

$Φ_{t o t a l} = \oint_{c}^{} \vec{g} . \hat{n} d A = - 4 π G m_{i n t .} s e n d o m_{i n t .}$

$ϕ_{t o t} = \oint_{c} \vec{E} \cdot \hat{n} d A = 4 π k {q_{i n t}}_{c}$

$∆ V = V_{b} - V_{a} = - \int_{a}^{b} \vec{E} . d \vec{l}$

$\oint \vec{E} . d \vec{l} = 0$

$V (r) = - \int_{a}^{r} \vec{E} . d \vec{l}$

$\vec{E} = - \vec{\nabla} V (r)$

$V (p) = V_{1} + V_{2} + V_{3} + \dots V_{N} = \sum_{i = 1}^{N} k \frac{q_{i}}{r_{i}}$

$V (r) = - \int_{a}^{r} \vec{E} . d \vec{l} o u \vec{E} = - \vec{\nabla} V (r)$

$\begin{matrix} Q_{total} = Q_{1} + Q_{2} + \dots + Q_{N} \\ ΔV \cdot C_{eq} = ΔV (C_{1} + C_{2} + \dots + C_{N}) \\ C_{eq} = \sum_{i = 1}^{N} C_{i} \end{matrix}$

$\begin{matrix} Δ V = V_{1} + V_{2} + \dots + V_{N} \\ \frac{Q}{C_{e q}} = \frac{Q}{C_{1}} + \frac{Q}{C_{2}} + \dots + \frac{Q}{C_{N}} \\ \frac{1}{C_{e q}} = \sum_{i = 1}^{N} \frac{1}{C_{i}} \end{matrix}$