Definição
Introdução aos conceitos termodinâmicos de temperatura e dilatação.
PROPÓSITO
Compreender os conceitos de calor e suas formas de propagação, assim como a primeira, a segunda e a terceira lei da termodinâmica, além das concepções envolvidas no funcionamento de máquinas térmicas e refrigeradores.
OBJETIVOS
Módulo 1
Definir os conceitos de calor, calor sensível e calor latente, além da capacidade térmica e das formas de transmissão de calor
Módulo 2
Reconhecer as três leis da termodinâmica
Módulo 3
Identificar a teoria termodinâmica por trás do funcionamento de máquinas térmicas e refrigeradores
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e uma calculadora científica, ou use a calculadora de seu celular ou computador.
Introdução
Bem-vindos ao estudo introdutório à Física de Calor
MÓDULO 1
Definir os conceitos de calor, calor sensível e calor latente,
além da capacidade térmica e das formas de transmissão de calor
Calor
A energia se manifesta ao nosso redor de muitas formas distintas. Ela, no entanto, precisa retornar ao meio ambiente — e, em geral, retorna de forma degradada.

O calor é a forma mais degradada da energia que conhecemos; por isso, ele merece uma atenção especial. Definiremos neste módulo o significado dele, destacando ainda como sua compreensão ajudou a humanidade a progredir tecnologicamente.
Definição de calor
Calor é o termo utilizado em física para definir a transferência de energia que ocorre devido à diferença de temperatura entre dois ou mais corpos. Apesar de ser energia, ele possui um sentido: o calor flui espontaneamente do corpo de maior temperatura, ou seja, o mais quente, para o de menor temperatura, ou seja, o mais frio.

A energia, portanto, se transfere espontaneamente sempre do corpo quente para o frio.
Essa transferência energética ocorre até que o equilíbrio térmico seja atingido. Há duas formas de transferi-la de um sistema físico para outro. A primeira é por meio da realização de trabalho; a segunda, por meio do calor.
Na Física, representamos o calor pela letra Q. Por se tratar de energia, sua unidade no Sistema Internacional de Unidades (SI) é o Joule (J). No entanto, é muito mais comum o calor ser expresso em calorias (cal). Uma caloria possui um valor aproximado de 4,18 Joules:
Essa relação é de suma importância para que saibamos realizar a conversão de uma unidade para outra.
Vamos demonstrar como é possível converter as unidades de energia?

Para aquecer certa quantidade de água, são necessários 2.300cal. Qual o valor dessa energia no SI?
Para conhecer esse valor, deve-se fazer uma conversão de calorias para Joules. Neste caso, basta utilizar uma simples regra de três:
Ou seja, 2.300cal é igual a 9.614J.
Podemos verificar, grosso modo, que, em uma conversão de calorias para Joules, ocorre o seguinte: pega-se o valor dado em calorias e o multiplica por 4,18.
Isso significa que, para converter de Joules para calorias, basta dividir o valor em Joules por 4,18. A figura a seguir indica um esquema que ajuda a visualizar essa conversão.
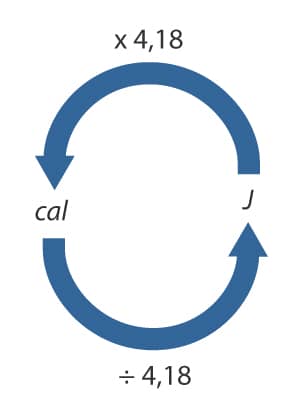
Façamos agora uma conversão inversa:
Exemplo
Como converter 8.500J para calorias?
Podemos observar na figura acima que basta dividir o valor 8.500J por 4,18:
Ou seja, 8.500J são iguais a 2.033,49 cal.
Calor e transferência de energia
A transferência de energia na forma de calor pode ocorrer de duas maneiras:
a) Calor sensívelTrata-se da troca de energia entre corpos na forma de calor de tal maneira que haja uma mudança de temperatura sem ocorrer uma modificação no estado físico da matéria. O corpo, portanto, não sofre fusão, evaporação, sublimação, etc.
Matematicamente, o calor sensível é calculado como:
Em (1), m é a massa do corpo. Quando a unidade de energia é o Joule, m é dado em quilogramas (kg); porém, quando essa unidade se refere a calorias, m é dado em gramas (g). Já c corresponde ao calor específico do corpo, que é uma constante e depende do material aquecido ou resfriado.
Saiba mais
O livro Handbook of physics contém uma tabela com o calor específico de todos os materiais conhecidos.
No SI, a unidade e medida do calor específico é o Joule por quilograma Kelvin . Contudo, se a energia for dada em calorias, esse calor terá unidades de calorias por grama graus Celsius .
Já significa a variação de temperatura. Se a energia estiver em Joules, as temperaturas deverão estar em Kelvin (K), mas, se elas estiverem em função das calorias, precisarão constar em Celsius (°C).
Dica
Recordemos que, matematicamente, a variação de temperatura é determinada pela diferença entre a temperatura final (T) e a inicial (T0):
Conseguiremos compreender melhor esse conceito acompanhando a solução de mais um exemplo:

Um litro de água está sendo aquecido pela chama de um fogão até o ponto de ferver. A densidade dela é de 1g/cm³; seu calor específico, de 1cal/g°C. Considerando que a água é levada à chama com uma temperatura de 20°C, determine a quantidade de energia que deve ser fornecida à água para que ela possa ferver.
Para reforçar seu aprendizado, abordaremos, neste vídeo, sobre a quantidade de energia necessária para ferver água.
Atenção
Um corpo resfriando, ou seja, que diminui sua temperatura cede energia para o meio ambiente. Dessa forma, o que se obtém como resultado é uma quantidade de energia negativa. O sinal negativo, neste caso, significa que o corpo está cedendo (perdendo) energia, e não que a está ganhando.
Calor latente
É a unidade de medida física relacionada à quantidade de energia que, em forma de calor, um corpo deve receber ou ceder para mudar de fase.
Exemplo
Nessas mudanças de fase, pode-se passar do estado sólido para o líquido, do líquido para o gasoso e vice-versa etc.
Matematicamente, o calor latente é dado por:
Em (3), a massa m é dada em gramas ou quilogramas nas mesmas circunstâncias discutidas acima em (1). Já o L é chamado de calor latente: trata-se da energia necessária para um grama do material mudar de fase. Sua unidade no SI é o Joule por quilograma . Contudo, em função da unidade de energia cal, ela é expressa por .

Um litro de água se encontra a 100°C. O calor latente de evaporação dela é igual a . Qual é a quantidade de energia necessária para evaporar toda essa massa de água?
Note que temos de determinar a massa da água, mas essa determinação já foi feita no exemplo acima. Desse modo, sabemos que um litro de água corresponde à massa de 1kg de água.
Aplicando a equação (3), temos:
Ou, em calorias:
Nosso resultado indica que é necessária uma energia de 2.256kJ ou 539,71kcal para evaporar 1kg de água. No entanto, se a reação física fosse inversa, ou seja, o vapor d’água condensado em líquido, consideraríamos o calor latente da água como – 2256 . Neste caso, veríamos que o vapor precisaria perder -2.256kJ (-539,71kcal) de energia para poder condensar.
Vejamos agora outro exemplo um pouco mais complexo:
Determinaremos a energia necessária a fim de que uma pedra de gelo de 0,5kg a -4°C se transforme em um vapor d’água a 100°C.
Primeiramente, vamos aos dados:
Agora precisamos raciocinar: como ocorre esse aquecimento de -4°C a 100°C? Tal resposta pode ser dividida em quatro etapas:
1. A temperatura de 0,5kg de gelo (500g) aumenta de -4°C a 0°C, ponto em que muda de fase (sólido para líquido).
Nesta primeira etapa, portanto, obtemos calor sensível:
2. Agora que o gelo está a 0°C, ele derreterá; logo, ele mudará da fase sólida para a líquida.
Assim, chegamos à segunda etapa, a do calor latente:
3. Nesta etapa, temos 500g de água, pois todo o gelo derreteu.
Com isso, essa água será aquecida de 0°C a 100°C, o que nos remete ao calor sensível:
4. O que resta é a água a 100°C evaporar. Para isso, é necessário mudar de fase, ou seja, passar do líquido para o vapor.
Desse modo, temos calor latente:
No entanto, todas as demais energias calculadas até agora estão em calorias; dessa forma, precisamos converter a energia Q4 para calorias:
Já podemos determinar a energia total que a massa de gelo de 0,5kg teve de absorver para se tornar um vapor d’água a 100°C. Basta, para isso, somar a energia das quatro etapas:
Ou, multiplicando por 4,18, temos:
As quatro etapas calculadas podem ser apresentadas na forma de um gráfico, o que facilita a visualização das fases de transformação do gelo em vapor. Ele está demonstrado na figura a seguir:

No gráfico, podemos observar que, em Q2 e Q4, onde calculamos calor latente, existe um patamar horizontal. Isso demonstra que a transformação de fase ocorre sem haver mudança na temperatura.
Capacidade térmica
Representada pela letra C (maiúscula), a capacidade térmica indica a quantidade de energia que deve ser absorvida ou cedida por um corpo para alterar a sua temperatura em 1°C.
Ela é determinada pela razão entre a energia e a variação da temperatura.
Matematicamente, representamos isso como:
Sua unidade de medida é o Joule por Kelvin (J/K) no SI ou calorias por graus Celsius (cal/°C).
Outra forma de determinar a capacidade térmica de um corpo é por meio do produto entre sua massa e seu calor específico:
Com a informação de (5), podemos reescrever (1), que foi visto acima, como:
Dica
Note que (6) é equivalente a (4).
A capacidade térmica também pode ser observada no gráfico exposto acima como o coeficiente angular da reta que representa o calor sensível.
Veja o caso a seguir:

Considere que quatro gramas de água estão em um calorímetro de capacidade térmica igual a 0,8cal/°C. Sabendo que o calor específico da água é igual a 1cal/g°C, encontre a quantidade de energia necessária para fazer o conjunto calorímetro-água sofrer um aumento de temperatura de 98°C.
Neste caso, tanto o calorímetro quanto a água aquecem; desse modo, precisamos determinar o aquecimento de ambos.
Primeiramente, utilizaremos a equação (6) para determinarmos a energia necessária a fim de gerar o aquecimento do calorímetro:
Em seguida, empregaremos a equação (1) para determinarmos a quantidade de energia necessária para aquecer a massa de 4g de água:
No total, a energia necessária para aquecer o sistema é:
Troca de calor em um calorímetro (conservação da energia térmica)

Utilizaremos agora tanto as teorias relativas ao calor sensível e ao latente quanto a de capacidade calorífica para compreendermos como ocorre a troca de calor entre os corpos no interior de um calorímetro, ou seja, em um recipiente que impede sua troca com o meio externo.
Nesta situação, vemos que:
Veja o caso a seguir:

Em um calorímetro de capacidade térmica de 0,3cal/°C com 200g de água a 20°C, é posto um objeto metálico de 1g a uma temperatura de 212°C. Esse objeto possui capacidade térmica de 0,15cal/°C.
Considerando o calor específico da água como 1cal/g°C, qual é a temperatura de equilíbrio do sistema?
Ao misturarmos algo quente com outro frio, obtemos o equilíbrio térmico em uma temperatura intermediária entre o quente e o frio. Neste caso, vamos encontrar uma que esteja entre 20°C e 212°C.
O calorímetro também participa da troca de calor, então, dessa maneira, temos:
3. Calorímetro:
2. Água aquecendo até a temperatura de equilíbrio:
3. Cubo de metal resfriando até a temperatura de equilíbrio:
Como não há troca de energia com o meio externo, esses materiais trocam de energia entre si; então, diante disso, a troca de energia total é nula, pois essa energia continua sendo a mesma.
Dessa forma, podemos matematicamente afirmar que:
A temperatura do equilíbrio se dá em 20,14°C.
Podemos apontar ainda que, a uma temperatura de 212°C, 1g desse metal aumenta em 0,14°C o conjunto “calorímetro + 200g de água”, que, inicialmente, se encontra a 20°C.
Propagação do calor
A propagação de calor do corpo quente para o frio pode ocorrer de três formas distintas:
A transferência ocorre por contato direto entre os dois corpos.

Colocamos uma pedra de gelo em um copo de água a uma temperatura ambiente. Como a água e o gelo estão em contato direto, a água transfere energia (na forma de calor) para o gelo até que o equilíbrio térmico seja estabelecido.
É a transferência de energia por meio de um fluido.

Exemplo
No cozimento de alimentos, o fogo aquece o fundo de uma panela. Ela transfere o calor para a água, agitando suas moléculas. Essa agitação, por sua vez, transfere energia na forma de calor para o alimento, cozendo-o.
Então, neste caso, temos a transferência de energia na forma de calor do fogo para o alimento, através do fluido que é a água. Isto é a convecção.
Transferência de energia na forma de calor que ocorre tanto no vácuo, como em meio material, porém, não precisa de meio material para se propagar. Essa propagação ocorre por meio de emissão de fótons.

Mão na Massa

Teoria na prática
Utilizaremos agora as informações sobre conservação da energia térmica para determinarmos a quantidade de gelo que se transforma na seguinte situação:
Em um calorímetro ideal de capacidade térmica desprezível com uma pedra de 200g de gelo a -4°C, são adicionados 150g de água a 10°C.
Considerando o calor específico do gelo 0,5cal/g°C e o da água, 1cal/g°C, assim como o calor latente de fusão igual a 540cal/g, determine a quantidade de gelo que derrete durante a troca de calor até que seja atingido o equilíbrio térmico em 0°C.
Primeiramente, determinaremos quanta energia é gasta para aquecer o gelo de -4°C para 0°C:
Em seguida, apontaremos quanta energia foi retirada da água a fim de que ela resfriasse de 10°C para 0°C:
Por fim, calcularemos a quantidade de energia necessária para fazer certa massa de gelo se transformar e virar água:
Basta agora somar as energias e igualar a zero:
Assim, nas condições descritas, verificamos que, ao se alcançar o equilíbrio térmico em 0°C, 2,04g de gelo se transformam em água em 0°C.
Com isso, ao final, temos 197,96g de gelo e 152,04g de água.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Reconhecer as três leis da termodinâmica
Introdução
A termodinâmica, assim como qualquer parte da Física, é regida por leis. Elas explicam, com exatidão e clareza, como ocorre, por exemplo, a variação de temperatura em um corpo e de que maneira o calor se comporta.

Por meio dessas leis, é possível construir máquinas térmicas que realizam trabalho mecânico, ou outras que produzem tal trabalho, com o objetivo de gerar calor. Neste módulo, as conheceremos e entenderemos como esse tipo de conhecimento iluminou o caminho evolutivo da humanidade.
Primeira lei da termodinâmica
Também conhecida como princípio de Joule, a primeira lei da termodinâmica é a versão termodinâmica da lei de conservação da energia mecânica, pois ela assume que diversas formas de trabalho podem ser convertidas em outras formas de energia.
De acordo com seus preceitos, a energia transferida na forma de calor (Q) é igual à soma da variação da energia interna (∆U) do sistema termodinâmico analisado com o trabalho (W) por ele sofrido ou realizado. Podemos observar isso nesta fórmula:
Saiba mais
A primeira lei da termodinâmica foi estabelecida por Rudolf Clausius (1822-1888). O físico e matemático alemão é considerado um dos fundadores deste ramo da ciência: a termodinâmica.
Quando o calor Q é medido em calorias, a energia interna e o trabalho também devem estar na unidade de calorias; no entanto, se Q estiver em Joules, a energia interna e o trabalho também deverão estar.
Entendemos que o calor de um corpo é obtido pela soma de duas parcelas de energia, mas o que significa essa energia interna?
Ela é a soma de toda a energia mecânica das partículas que compõem o sistema, ou seja, trata-se do somatório de todas as parcelas de energia cinética das partículas com a energia potencial delas.
A energia interna é considerada uma propriedade do sistema, pois depende somente dos estados inicial e final do processo termodinâmico. Tendo isso em vista, podemos fazer duas afirmações:
Quando Q é positivo, ou seja, Q > 0, o sistema está ganhando calor.
Quando Q é negativo, ou seja, Q < 0, ele o está cedendo.
Pela primeira lei da termodinâmica demonstrada na equação (8), ainda podemos fazer a seguinte afirmação: quanto maior for a energia interna de um sistema, maior será sua capacidade de realizar um trabalho. No entanto, trata-se de uma convenção a indicar que:
Quando o sistema expande e realiza trabalho, W > 0; porém, neste caso, ele está perdendo energia para o meio ambiente.
Quando se contrai e recebe trabalho, W < 0; no entanto, neste caso, o sistema está recebendo energia do meio ambiente.
Em geral, estuda-se o sistema termodinâmico voltado para os gases. O trabalho de um gás é dependente de sua pressão (P) e da variação de seu volume (∆V):
Nesta equação, a pressão é dada em Pascal (Pa) e a variação do volume, em metros cúbicos (m³).
A primeira lei da termodinâmica admite casos especiais que considerem o tipo de transformação termodinâmica que o sistema está sofrendo. Vamos analisá-los agora:
| Transformação | Condição | 1ª lei da termodinâmica |
|---|---|---|
| Isotérmica | ||
| Isocórica | ||
| Isobárica | ||
| Adiabática | ||
| Expansões livres |
Isotérmica
Condição termodinâmica em que a transformação ocorre a uma temperatura constante.
Isocórica
Condição termodinâmica em que a transformação ocorre a um volume constante.
Isobárica
Condição termodinâmica em que a transformação ocorre a uma pressão constante.
Adiabática
Condição termodinâmica em que a transformação ocorre sem troca de calor com o ambiente externo.
Expansões livres
Expansão de um gás sem que haja um recipiente. Exemplo: vapor d’água expandindo livremente para o ar e se dissipando na atmosfera.
Verificaremos agora uma exemplificação da aplicação da primeira lei da termodinâmica:
Exemplo
Um determinado gás está confinado em um recipiente de 1m³ a uma pressão de 1atm (105Pa), quando recebe uma quantidade de 2.654.789cal de energia na forma de calor e se expande para 3m³.
Qual é sua variação de energia interna?
Neste vídeo, abordaremos a determinação da variação de energia interna.
Segunda lei da termodinâmica: o conceito de entropia
A primeira lei da termodinâmica postula que há conservação de energia em qualquer transformação termodinâmica. A segunda lei, por sua vez, determina as condições necessárias para a ocorrência espontânea de transformações termodinâmicas. Ela foi inicialmente estabelecida como um conceito empírico.
Conceito Empírico
Conceito estabelecido por intermédio da coleta de dados por observação de diversos experimentos físicos.
A partir disso, foi estabelecido o seguinte: para que haja um trabalho líquido em um sistema termodinâmico, ele precisa operar entre duas fontes térmicas mantidas a temperaturas distintas.
A segunda lei da termodinâmica expressa, desse modo, que a quantidade de entropia de qualquer sistema termodinâmico isolado tende a aumentar com o passar do tempo até atingir um valor máximo.
Isso significa que, para um sistema isolado, a entropia nunca diminui.
Mas o que é a entropia?
Ela é uma grandeza termodinâmica que mede o grau de liberdade molecular do sistema físico observado. Esse grau está associado à quantia de possibilidades com a qual as partículas podem se distribuir em níveis energéticos quantizados.
Matematicamente, definimos a entropia (∆S) como a razão entre a variação da energia em forma de calor (∆Q) e a temperatura do (T):
A unidade de medida da entropia no SI é o Joule por Kelvin (J/K); todavia, também é comum ela ser expressa em calorias por graus Celsius (cal/°C).
Como dissemos, em um sistema isolado, a entropia aumenta com o passar do tempo. Desse modo, verificamos que:
A figura a seguir ilustra a entropia e o aumento da desordem molecular:
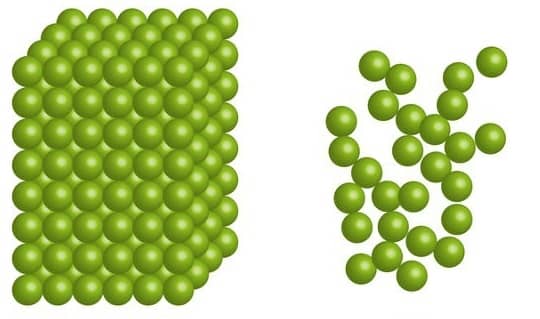
Com a equação (11), podemos afirmar que a entropia é um grau de desordem de um sistema físico termodinâmico. Vejamos de que forma ela se manifesta em dois tipos de sistema:
- Sistema isolado: essa desordem somente tende a aumentar com o passar do tempo;
- Sistema fechado: a entropia se mantém ou aumenta. Quando ela aumenta, essa transformação é irreversível.
No entanto, se o sistema não for isolado, havendo, portanto, troca de calor com o meio ambiente, pode haver nele uma redução de entropia.
1. Existe certa quantidade de água no interior de um calorímetro ideal, ou seja, um recipiente que impede a troca de calor com o meio externo. Inicialmente com uma temperatura de 20°C, ela recebe alguma quantidade de energia e fica com 70°C. Esse incremento na temperatura aumentou sua energia interna ∆U e, por sua vez, a entropia dela, pois as moléculas da água passaram a ficar mais agitadas. Como o calorímetro é ideal, essa energia dada para a água nunca será cedida ao meio ambiente. O fato de a temperatura dela não poder diminuir garante que a entropia do sistema não vai baixar.
2. Em vez de em um calorímetro, a água está agora contida em um copo de vidro sobre uma mesa. Ao aquecer de 20°C para 70°C, a entropia vai aumentar. No entanto, como existe uma troca de calor com o meio ambiente, a água começa, com o tempo, a diminuir sua temperatura gradativamente até retornar àquela registrada inicialmente (20ºC). Essa redução da temperatura diminui a energia interna do sistema, o que também diminui a entropia do sistema.
Observaremos agora outro exemplo com uma aplicação da teoria da segunda lei da termodinâmica:
Isolado do meio externo, determinado sistema físico sofre uma variação de energia interna de 5.000.000J, se equilibrando em uma temperatura de 795K.
Qual é a sua variação de entropia?
De acordo com a equação (10), notamos que:
Substituindo os valores, temos o seguinte:
Terceira lei da termodinâmica
Desenvolvida pelo químico Walther Nernst, a terceira lei da termodinâmica postula que a entropia de um sistema no zero absoluto (0K) é constante. Essa afirmação se justifica pelo fato de que qualquer sistema termodinâmico a 0K (-273°C) existe em seu estado fundamental.
A explicação para isso é que, a 0K, não existe vibração molecular. Dessa forma, não há energia interna. Sem ela, não se registra desordem — e, sem desordem, a entropia é nula.
Matematicamente, a terceira lei da termodinâmica é descrita como:
Todo corpo possui uma vibração molecular. Essa vibração é dependente da temperatura; com isso, quanto maior for a temperatura, maior será a vibração molecular e, por consequência, a desordem das moléculas. Contudo, o contrário também é valido: quanto menor for a temperatura, menores serão o desarranjo molecular e a entropia.
A terceira lei da termodinâmica prevê que a entropia só é nula quando a vibração molecular também é nula.
Isso só pode ser alcançado na temperatura de zero absoluto, que corresponde ao zero Kelvin (0K). Em 0K, as moléculas assumem um arranjo perfeito.
A figura a seguir ilustra o comportamento da entropia com a diminuição da temperatura:
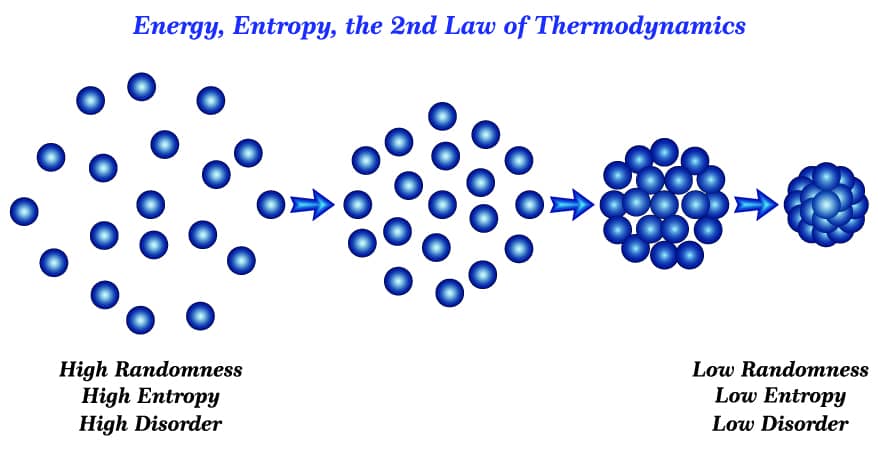
Mão na Massa

Teoria na prática

Vimos que o trabalho realizado por um gás é obtido pelo produto entre a pressão e a variação de seu volume (). No entanto, tal equação tem funcionalidade apenas para os casos em que a pressão é constante.
Há muitos sistemas termodinâmicos em que o gás realiza um trabalho em uma condição na qual a pressão não é constante. Neste caso, para determinar o trabalho, é necessário montar um gráfico denominado diagrama PV (pressão por volume). Seu trabalho é determinado pelo cálculo da área da forma geométrica gerada pelas curvas de transformações térmicas
Tendo isso em vista, consideraremos a seguinte situação:
Determinado gás possui 3m³ de volume e está a uma pressão de 12Pa. De repente, ele sofre uma transformação: o estado final dele passa a ser de um volume de 10m³ e pressão de 6Pa.
Indique o trabalho realizado por esse gás.
Primeiramente, precisamos montar o gráfico PV da seguinte maneira:
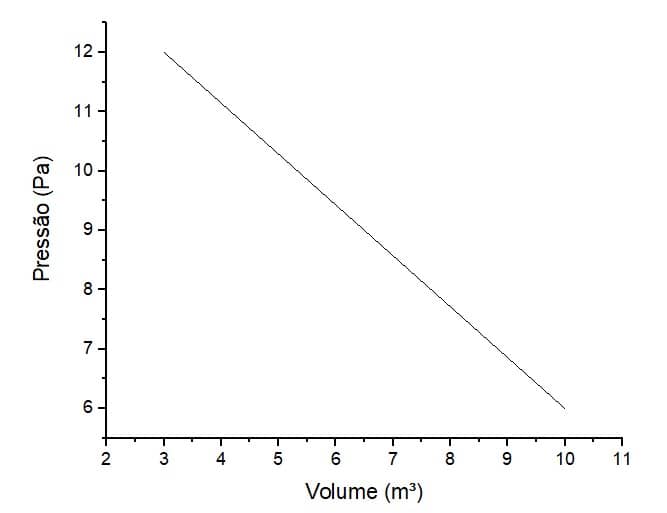
Em seguida, determinaremos a figura geométrica, a qual, ao se verificar a área sobre a curva, é montada da seguinte forma:
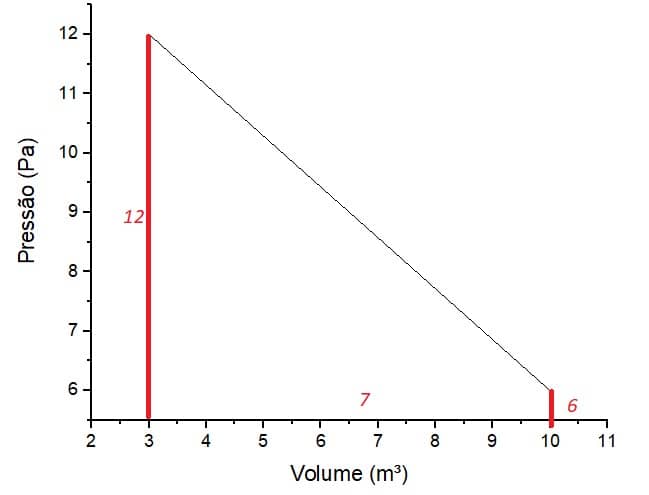
Podemos observar que a área sobre a curva montou um trapézio de base maior 12Pa, base menor 6Pa e altura 7m³. Então, para o cálculo do trabalho, calcularemos a área desse trapézio:
Neste caso, em que a transformação termodinâmica promove uma mudança de volume e pressão, o trabalho do gás foi determinado pela área sobre a curva do trabalho plotada em um gráfico PV.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Identificar a teoria termodinâmica por trás do funcionamento de
máquinas térmicas e refrigeradores
Máquinas térmicas

Uma máquina térmica trabalha absorvendo calor do meio ambiente à sua volta e convertendo-o em trabalho útil. Porém, para que tal conversão seja realizada, essa máquina depende de uma substância de trabalho (em geral, um fluido).
Um exemplo simplório disso é o funcionamento de uma máquina que funciona a vapor d’água.
Vapor d’água
O vapor d’água é a substância de trabalho que, ao se expandir, realiza um trabalho mecânico sobre uma roda e a faz girar.
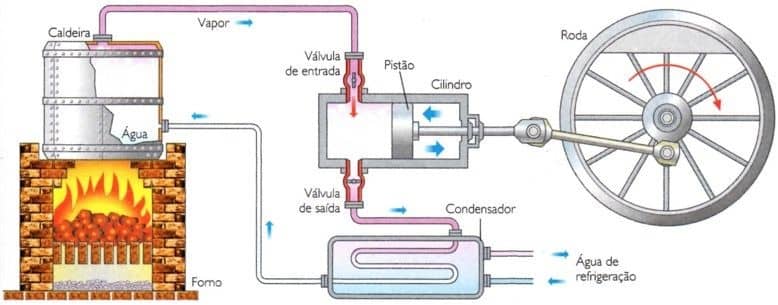

Outro exemplo cotidiano é a máquina térmica que faz um automóvel se mover, ou seja, o motor de um automóvel. Neste tipo de motor, o líquido de trabalho é a mistura entre aquele utilizado para a combustão, como gasolina, etanol, GNV e diesel, e o ar.
Uma máquina térmica precisa funcionar continuamente, sempre convertendo calor em trabalho mecânico (trabalho útil). Para que isso seja possível, tal máquina deve trabalhar em um ciclo fechado no qual ocorrem diversos processos termodinâmicos chamados de tempos.
Máquina de Carnot: Ciclo de Carnot, o ciclo ideal
Para aprofundar nosso conhecimento sobre as máquinas térmicas, é necessário recorrer à ciência da termodinâmica e verificar como suas leis podem nos ajudar a compreender mais sobre o funcionamento delas.
Funcionamento
Existem diversos tipos de motores; logo, há muitos tipos de máquinas térmicas. A máquina térmica de Carnot se baseia no ciclo de transformação termodinâmico de Carnot.
Máquina térmica de Carnot
O ciclo de Carnot foi desenvolvido antes do desenvolvimento das duas leis da Termodinâmica. É importante mencionar que a máquina de Carnot é uma máquina ideal, o que significa que nenhuma máquina térmica consegue alcançar a sua eficiência.
Esse ciclo mostra que a máquina térmica de Carnot é a mais eficiente para a conversão de calor em trabalho útil. Na figura a seguir, podemos observar um esquema representativo do funcionamento dessa máquina.
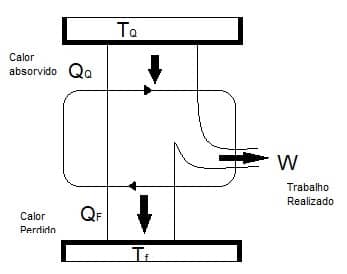
A máquina de Carnot funciona com duas fontes:
De temperatura quente (TQ): Fornece ao fluido de trabalho uma quantidade de calor (QQ).
De temperatura fria (TF): Retira calor (QF) desse fluido.
Dica
Chamar uma fonte de quente e outra de fria é uma convenção apenas para afirmar que TQ > TF e, por sua vez, que QQ > QF.
Contudo, a energia absorvida na fonte quente não é integralmente aproveitada para realizar o trabalho. Desse modo, em tal situação, a restante é retirada do fluido pela fonte fria. Ao despejá-la nessa fonte, o fluido de trabalho reinicia o ciclo para que o trabalho mecânico seja realizado constantemente.
Já a energia que transcorre pelo fluido na fonte quente, é a energia total que o fluido recebe. Assim, assumindo que não há perda de calor para o meio ambiente, podemos estabelecer que a retirada de energia nessa fonte é igual à soma entre o trabalho realizado pela máquina e a energia despejada na fonte fria:
Observemos agora outra figura. Ela apresenta um diagrama pressão por volume (PV) do ciclo de Carnot. O sentido das transformações termodinâmicas do ciclo está indicado pelas setas. Podemos perceber que esse ciclo é percorrido no sentido horário.
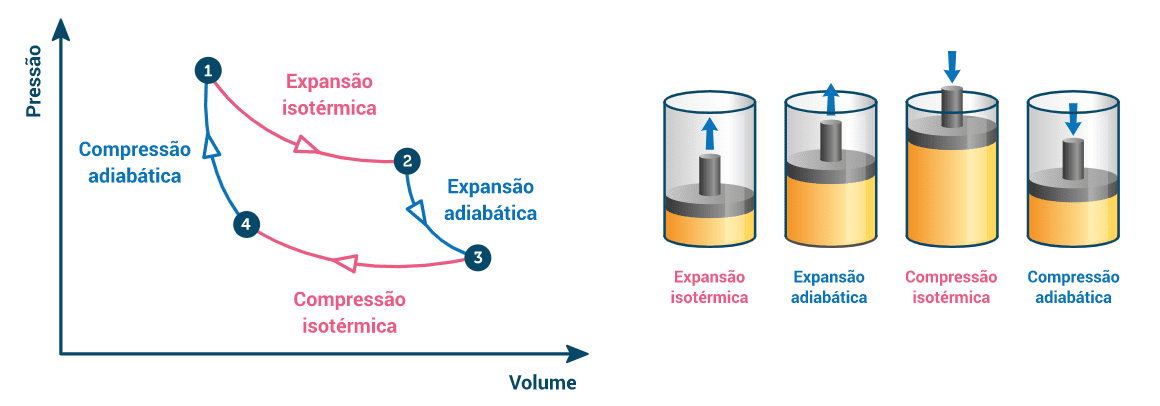
A figura acima também apresenta o funcionamento de um cilindro ideal, que, fabricado de material isolante, contém um fluido. Esse cilindro nos ajuda a compreender o funcionamento mecânico do ciclo de Carnot.
Para isso, consideraremos que:
- O fluido é um gás ideal;
- O cilindro se encontra entre uma fonte quente e uma fria.
No ponto 1 da figura, a fonte quente cede energia para o fluido de trabalho, havendo uma transformação isotérmica pelo fato de a temperatura da fonte quente ser constante.
Completada a transformação, o fluido atinge o ponto 2 do diagrama PV: neste ponto, ele sofre uma transformação de expansão adiabática e, em seguida, realiza o trabalho sobre o cilindro, empurrando o êmbolo até a altura máxima que ele pode assumir no local (realiza trabalho mecânico sobre o cilindro (W).
Em seguida, o fluido atinge o ponto 3 do diagrama. Ali, ele perde energia para a fonte fria: como a temperatura dessa fonte é constante, o fluido sofre uma compressão isotérmica e atinge o ponto 4 do diagrama.
No último ponto, o êmbolo realiza um trabalho adiabático sobre o fluido, comprimindo-o. Isso faz o ciclo retornar para o ponto 1 e, daí em diante, se repetir indefinidamente. No ciclo termodinâmico da figura acima, o trabalho pode ser medido pelo cálculo da área no interior da curva formada pelo ciclo.
Dica
O processo é equivalente ao que foi feito no tópico Teoria na prática do módulo 2.
Determinação da eficiência
Em qualquer tipo de máquina, o maior interesse é converter o máximo possível de energia em trabalho útil. Essa conversão é chamada de rendimento .
Matematicamente, esse rendimento é determinado pela razão entre o trabalho realizado pela máquina (W) e a quantidade de energia total cedida a ela, o que, no caso de uma máquina térmica, corresponde ao calor fornecido pela fonte quente QQ.
Diante disso, matematicamente temos:
Mensurar o trabalho realizado é uma tarefa difícil. Por isso, precisaremos reescrever a equação (13) para podermos deixar o rendimento em função de parâmetros conhecidos:
Temperatura quente (TQ)
Temperatura fria (TF)
Em seguida, tiraremos da equação (12) que . Substituindo W em (13), obtemos o seguinte:
Reescrevendo (14), temos:
Simplificando:
Neste tipo de transformação, não há mudança de fase. Desse modo, podemos escrever QF e QQ em função da teoria de calor sensível:
Note que as equações do calor sensível foram descritas em função de TF e TQ – e não de DTF e DTQ. Afinal, as transformações são isotérmicas.
Simplificando (16), verificamos que:
Da equação (17), deduzimos que, conhecendo as temperaturas das fontes fria e quente, é possível determinar o rendimento dessa máquina térmica.
Atenção
Para esse cálculo, a temperatura deve ser convertida para Kelvin. Caso contrário, o rendimento calculado será fictício.
Podemos escrever a equação (17) na forma porcentual da seguinte maneira:
Como TF < TQ, a eficiência da máquina térmica é menor que 100%.
A máquina térmica perfeita seria aquela cujo rendimento fosse de 100%. Contudo, sabemos que isso não é possível no mundo real. Na equação (17), observamos que o rendimento só seria assim se TF = 0 ou TQ = ∞.
Veja o caso a seguir:

Um motor a combustão possui fonte quente em 500°C e fria em 190°C.
Qual é o seu rendimento?
Para determinarmos o seu rendimento, primeiramente precisamos converter a temperatura de °C para K:
Utilizando a equação (18), temos:
Assim, a quantidade de energia perdida para a fonte fria é igual a:
Apesar de o resultado do trabalho convertido ser de 40,10%, esse valor ainda é muito alto ao se tratar de uma máquina térmica real.
Exemplo
Um motor de automóvel converte de 23% a 30% de toda a energia gerada em trabalho, sendo o restante perdido na forma de calor.
Refrigeradores

Naturalmente, o calor flui de uma fonte quente para uma fria. Porém, é possível fazê-lo fluir da fonte fria para quente utilizando uma máquina térmica chamada de refrigerador.
Exemplo
Geladeira e ar-condicionado.
Para transferir calor do ambiente frio para o quente, o refrigerador utiliza o trabalho mecânico, contando, em geral, com o auxílio de um motor que possui um líquido de trabalho com um fluido pressurizado. Esse fluido tem como principal propriedade a capacidade de alterar seu estado físico — de gasoso para líquido — durante o ciclo dele.
A figura a seguir apresenta um esquema do funcionamento de um refrigerador. Observe que ele funciona de maneira oposta à de uma máquina térmica. Isso demonstra que ele retira energia da fonte fria e a deposita na quente quando o ciclo recebe trabalho do motor (ou compressor).
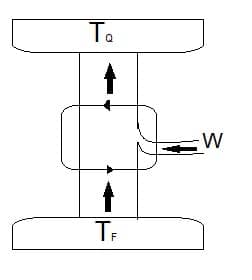
A eficiência do refrigerador é determinada pelo seu coeficiente de desempenho (K), o qual, por sua vez, é calculado pela razão entre a energia retirada da fonte fria (QF) e a consumida (W) no processo de refrigeração.
Matematicamente, temos isto:
No caso de um refrigerador ideal, ou seja, um refrigerador de Carnot, verificamos a seguinte representação:
Fazendo W=QQ-QF, observamos:
Fazendo Q = mcT, obtemos:
Simplificando:

Teoria na prática
Na indústria, o desempenho de um ar-condicionado doméstico é de e o desempenho de uma geladeira doméstica é de . Imaginemos que um refrigerador se encontra em um local onde a temperatura da fonte quente é de 42°C.
Para que sua eficiência seja de 2,5, qual deve ser a temperatura da fonte fria? Consideraremos um refrigerador de Carnot para essa solução.
Assista ao vídeo que aborda a determinação da temperatura ideal para rendimento e também apresenta a resolução desta questão.
Mão na Massa
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Neste tema, vimos que, na forma de calor, a energia pode ser transferida de um corpo para outro, dependendo apenas da diferença de temperatura entre eles. Verificamos ainda que há dois tipos de calor: o sensível, no qual o corpo muda a temperatura dele, embora preserve o estado físico da matéria, e o latente, em que essa variação cessa e a mudança de estado acontece.
Observamos também leis termodinâmicas que descrevem não só como a troca de calor ocorre, mas também como ela gera impactos nos corpos envolvidos. Por fim, explicamos como a humanidade utilizou esse conhecimento para produzir máquinas térmicas e refrigeradores com o objetivo de gerar uma melhoria da qualidade de vida na sociedade.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Compreendeu os conceitos de calor, calor sensível e calor latente, além da capacidade térmica e das formas de transmissão de calor.
Reconheceu a as três leis da termodinâmica.
Verificou a teoria termodinâmica por trás do funcionamento de máquinas térmicas e refrigeradores.


