Descrição
Princípios físicos de estática e dinâmica estabelecidos por Newton. Física Mecânica de corpos fluidizados.
PROPÓSITO
Aplicar os conceitos de densidade, volume e pressão, dos princípios de Arquimedes e Pascal e das equações da continuidade e Bernoulli nos problemas de estática e dinâmica dos fluidos.
PREPARAÇÃO
Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e uma calculadora científica ou use a calculadora de seu smartphone/computador.
OBJETIVOS
Módulo 1
Aplicar os conceitos de densidade, volume e pressão
Módulo 2
Aplicar os conceitos de Arquimedes e Pascal na estática dos fluidos
Módulo 3
Aplicar a equação da continuidade na dinâmica dos fluidos
Módulo 4
Aplicar a equação de Bernoulli na dinâmica dos fluidos
MÓDULO 1
Aplicar os conceitos de densidade, volume e pressão
Introdução
Ao estudar mecânica dos fluidos, devemos considerar duas grandezas físicas de suma importância: densidade e pressão.
Antes de nos aprofundarmos no conteúdo das leis que regem o comportamento dos fluidos, é necessário compreender tais grandezas.
Densidade ou massa específica
Chamamos a relação entre a massa de um corpo (m) pelo volume (V) que essa massa ocupa de densidade (d).
Matematicamente, a densidade é definida como:
A densidade possui unidade no Sistema Internacional de medidas (S.I.) de quilogramas por metros cúbicos , porém também é comum encontrarmos na literatura a densidade em gramas por centímetros cúbicos.
Como exemplo, podemos citar a densidade da água, que no Sistema Internacional de Medidas possui valor de
Porém, o mais comum de ser encontrado na literatura é a densidade da água como
Como, então, podemos fazer para converter as unidades da densidade?
Para compreender, vamos observar o exemplo abaixo:
Exemplo 1
Vamos verificar a conversão da densidade da água do S.I. primeiro para grama por centímetro cúbico e depois para quilograma por litro .
Esta última será realizada devido ao fato de a unidade litro ser a mais utilizada no mundo para expressar volume de líquidos.
1° Conversão de :
Devemos lembrar que em 1kg há 1000g, e que em 1m, há 100cm.
Então, partindo da informação de que a densidade da água no S.I. é de , a sua conversão para é:
2° Conversão de :
Devemos lembrar que 1l (um litro) é igual a 1dm (um decímetro cúbico)
Então, devemos fazer a conversão de m para dm.
Devemos lembrar também que 1m possui 0,1dm ou , ou ainda, .
Então, para converter a densidade da água de para , vamos seguir os seguintes passos:
A densidade de um corpo também é chamada de densidade absoluta.
Essa grandeza pode apresentar variação com aumento ou diminuição da temperatura do corpo, como, por exemplo:
A densidade do gelo a .
Enquanto a densidade da água à temperatura ambiente é de .
Densidade relativa
A densidade relativa é a densidade de um corpo expressa em função de outro corpo.
Vamos considerar que temos dois corpos, A e B, e que não conhecemos a densidade do corpo A, mas que podemos estimar a sua densidade em função da densidade do corpo B.
Isso é possível através da razão entre ambas as densidades, da seguinte maneira:
A densidade relativa é uma grandeza adimensional que, em geral, é expressa em função da densidade da água.
Exemplo 2
Considerando a densidade do gelo a 0°C como sendo 917kg/m³ e a densidade da água como 1000kg/m³, como podemos verificar se o gelo vai boiar ou afundar na água?
A resposta é simples: Verificando a densidade relativa do gelo em relação à água.
- Se essa densidade relativa for maior do que a unidade (maior que 1), o gelo afunda.
- Já se a densidade for menor ou igual, o gelo boia.
Vamos analisar então:
O corpo A é o gelo, assim: .
O corpo B é a água, assim: .
Definindo A e B, a densidade relativa do gelo em relação à água é igual a:
Note que o resultado foi menor do que 1, o que nos garante que o gelo flutuará, pois corpos de menor densidade ficam acima dos corpos de maior densidade.
Todavia, o valor encontrado nos informa também que a densidade do gelo a 0°C corresponde a 91,7% da densidade da água à temperatura ambiente, ou seja, que o gelo possui uma densidade 8,3% menor que a densidade da água.
Agora, vamos utilizar o conceito da densidade relativa para determinar a densidade de um corpo:
Exemplo 3
Em um experimento de densidade, foi determinado que um cubo de madeira possui uma densidade relativa em função da densidade da água à temperatura ambiente de 0,2.

Qual a densidade desse cubo de madeira?
Para determinar isso, temos do enunciado que , chamaremos a madeira do corpo e a água do corpo , assim:
Pressão
A pressão (P) é definida como sendo a razão entre a força aplicada (F) e a área (S) em que essa força é aplicada:
(3)
É importante ressaltar que para determinar a pressão, consideramos sempre a componente da força (F) que é normal à superfície da área especificada.
Da equação (3) podemos afirmar que quanto menor for a área em que a força é aplicada, maior é a pressão realizada pela força.
Para assimilar este conceito, vamos considerar o exemplo de um prego, como mostra a imagem a seguir.

Na imagem, temos um homem martelando um prego em uma tábua de madeira.
Para martelar, o homem apoia a ponta fina do prego na madeira e bate com o martelo na cabeça chata do prego, aplicando uma força sobre ele.
Nesse caso, a pressão que o prego aplica sobre a madeira é igual à força aplicada pelo martelo ao prego, dividida pela área da ponta fina do prego.
Todavia, por que o homem não faz o inverso?
Por que ele não apoia a parte chata na madeira, já que fica mais fácil de equilibrar o prego, e então bate na ponta mais fina?
Isso porque a cabeça chata do prego possui uma área muito maior do que a ponta do prego, então, ao aplicar a mesma força no prego com a martelada, o prego não conseguirá adentrar na madeira, devido à pressão, neste caso, ser muito menor.
Atenção
A pressão é uma grandeza escalar, ou seja, não possui direção nem sentido. Ela pode atuar tanto em sólidos, como também em líquidos e gases. Ela pode ser favorável ou desfavorável para uma aplicação na Física ou na Engenharia.
Beber com um canudo é uma aplicação simples da pressão utilizada por todos.

Você já se perguntou por que o líquido sobe o canudo?
Se a sua resposta diz que é devido à sucção, você está parcialmente correto, pois devemos complementar essa resposta.
O princípio mais importante sobre pressão é que: O fluido se move (flui) naturalmente do lugar de maior pressão para o de menor pressão.
Tudo bem, mas como isso se aplica ao caso de uma pessoa bebendo um líquido com auxílio de um canudo? Simples.
Para beber o líquido, instintivamente você suga todo o ar contido na sua boca para os seus pulmões, fazendo um ligeiro vácuo na sua boca, o que diminui a pressão nela.
Então, como a pressão na sua boca é menor do que a pressão do canudo dentro do líquido, este passa a fluir canudo acima até a sua boca.
A unidade de medida da pressão é o Pascal (Pa), e um pascal é igual a 1 Newton (N) por metro (m²):
(4)
Vamos solucionar dois exemplos para assimilar o conceito de pressão.
Exemplo 4
Considere que na retirada do petróleo é utilizada uma tubulação de 5 metros de raio, e que por ela passa uma massa de 2.000kg/s dessa substância.
Se a diferença de pressão entre o poço de petróleo e o reservatório para o qual ele é conduzido é de 127kPa (significa quilopascal, que é 103Pa), o petróleo sobe a tubulação com qual aceleração?
Solução
Para poder encontrar essa aceleração, teremos que utilizar primeiramente a equação (3):
O enunciado nos dá a diferença de pressão, então, como a equação (3) nos pode ser útil?
Podemos interpretar a diferença de pressão entre os dois ambientes como a pressão aplicada sobre o petróleo.
Assim, podemos dizer que:
Mas e a área?
A área a ser utilizada na equação (3) é aquela da seção reta da tubulação, que nesse caso, é a área de um círculo que é dada por:
Com essas informações, podemos determinar a força aplicando os devidos valores na equação (3):
Assumindo :
Agora que conhecemos a força, vamos utilizar a segunda Lei de Newton () para determinar a aceleração de movimentação desse fluido:
Definimos, assim, que a aceleração do fluido, tubulação acima, é de e que com essa aceleração, a tubulação consegue retirar 2000kg/s de petróleo do poço, ou seja, duas toneladas por segundo.
Exemplo 5
Considere um prego cuja cabeça possui raio de 1cm e comprimento de 5cm.
Na cabeça desse prego, é dada uma martelada com uma força de 500N.
Se a pressão na ponta do prego é 2,5 vezes maior do que na sua cabeça, qual é a área da seção transversal da ponta do prego?
Veja a solução desta questão, que aborda o assunto Pressão, no vídeo a seguir.
Diferença entre a cabeça e a ponta do prego

Teoria na prática
Considere que um projétil de 0,3kg de massa é disparado por um rifle a uma velocidade de 340m/s.
Esse projétil possui área da seção reta de sua ponta de
Ele atinge uma parede e para ao penetrá-la por 8cm.
Considerando que a força que desacelera o projétil até ele parar é constante, vamos determinar a pressão que ele exerce sobre a parede.
Primeiramente, para conhecer a força que desacelera o projétil, temos que encontrar a aceleração que desacelera o projétil. Para isso, nós vamos utilizar a equação de Torricelli:
A velocidade final (v) do projétil é zero. A velocidade inicial (v0) do projétil é 340m/s, e o espaço percorrido até parar é de 8cm, que é 0,08m. Assim:
Note que a aceleração é negativa, e esse resultado está correto, devido ao fato de a aceleração diminuir a velocidade do projétil até ele parar.
Então, conhecendo a massa do projétil e a sua aceleração, assim como a área da sua ponta, podemos determinar a pressão que o projétil exerce na parede, utilizando a equação (3), assim:
Mas se a pressão é uma grandeza escalar, como é possível que ela apresente um valor negativo?
A pressão apresentar um módulo negativo significa que o movimento do projétil está ocorrendo do ponto de menor pressão para o de maior pressão, ou seja, esse movimento é antinatural e só ocorre devido à energia cinética do projétil, que diminui pela ação da pressão até se extinguir e fazer com que o projétil pare.
Mão na Massa
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Aplicar os conceitos de Arquimedes e Pascal na estática dos fluidos
Introdução
Um fluido (líquido ou gás), quando incompressível, é capaz de transmitir a força aplicada a ele, molécula por molécula, sem apresentar perdas, o que permite muitas aplicações práticas no ramo da pressão.
Todo corpo que se encontra imerso em algum fluido e está em equilíbrio sofre pressão de todas as direções (pressão hidrostática), como também a ação de uma força vertical para cima chamada empuxo.
À vista disso, vamos verificar neste módulo os princípios que descrevem esses fenômenos.
Princípio de Pascal
O Princípio de Pascal recebeu esse nome por ter sido elaborado pelo físico e matemático francês Blaise Pascal, o qual estabeleceu que:
A pressão aplicada num ponto de um fluido em repouso transmite-se integralmente a todos os pontos do fluido.
Esse princípio permite, por exemplo, utilizar os macacos hidráulicos para levantar veículos, aplicando forças muito inferiores ao peso do automóvel, como mostra a figura.
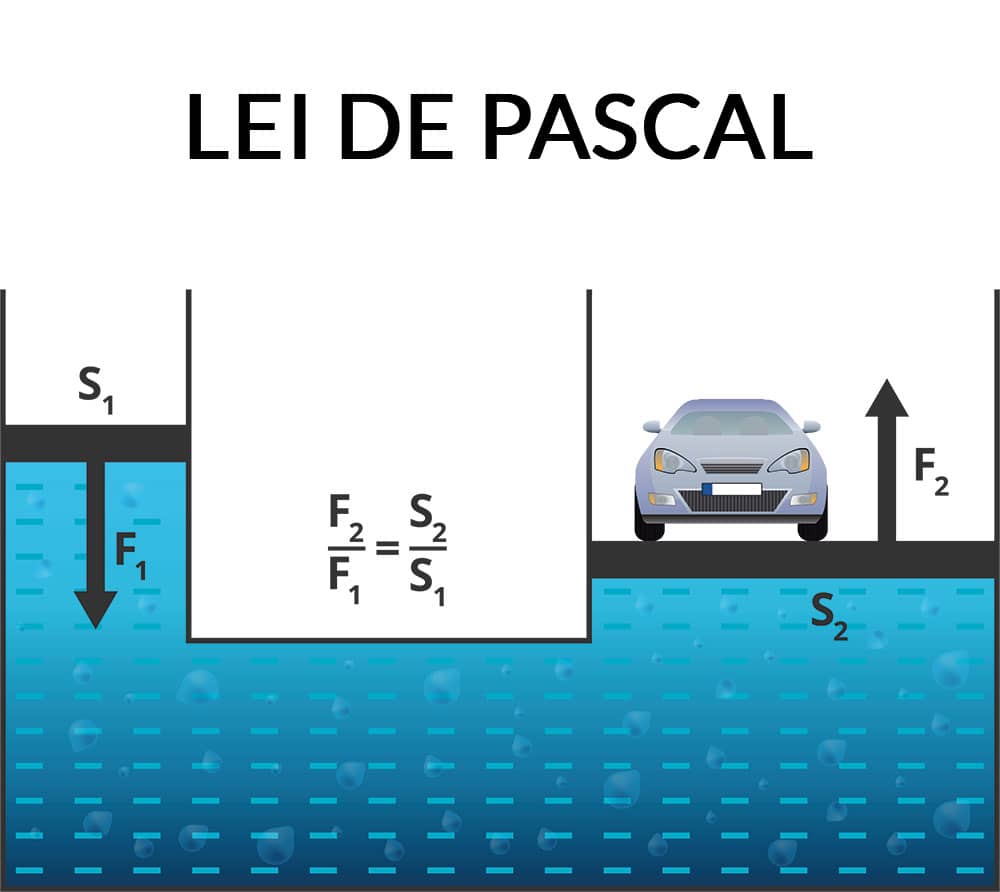
Vamos utilizar essa imagem para exemplificar a aplicação da Teoria da Pressão e explicar de maneira sucinta o Princípio de Pascal:
Exemplo 6
Considere que na figura, temos um elevador hidráulico, com um óleo de densidade de 0,8g/cm³, incompressível.
Do lado em que o carro se encontra, o raio da plataforma que o ergue é de 2m, e do lado onde a força é aplicada, o raio é de 0,5m.
Considerando que o carro tem um peso de 12.000N, qual deve ser a força realizada no lado da área S1, para erguer o carro com velocidade constante?
Solução
Para que a velocidade seja constante, a força resultante é nula, ou seja: FR = 0
Pelo Princípio de Pascal, a pressão aplicada se transmite integralmente a todos os pontos do fluido. Isso nos permite afirmar que:
A força F2 é a força peso do carro, e como estamos falando de um elevador hidráulico com plataforma cujo raio é 2m, podemos dizer que esse elevador é cilíndrico, e a área de sua seção reta é a de um círculo, assim:
Como queremos descobrir a força que devemos exercer para poder levantar o automóvel, temos que isolar F1:
Podemos simplificar a equação cortando o , devido a sua existência tanto no numerador quanto no denominador:
Substituindo os valores dados no enunciado, temos:
Se fizermos uma análise percentual, chegamos à conclusão de que a força necessária para erguer o automóvel é equivalente a 6,25% da força peso do automóvel, como está demonstrado a seguir:
A aplicação da equação (5) no exemplo nos mostra claramente que a redução da área aumenta consideravelmente a pressão aplicada, permitindo, assim, que o esforço humano seja minimizado.
Atenção
Apesar de o exemplo 6 ter sido solucionado utilizando a área de uma seção transversal circular, essa área pode assumir qualquer geometria plana, então, antes de solucionar qualquer tipo de problema envolvendo pressão, devemos nos atentar ao tipo de área de seção transversal ao qual a força é aplicada.
Lei de Stevin
A Lei de Stevin, ou Teorema de Stevin é um princípio físico que foi desenvolvido pelo físico, engenheiro e matemático Simon Stevin, o qual estabeleceu que a pressão absoluta existente em um líquido incompressível e de densidade homogênea, a certa profundidade h, é igual à soma da pressão atmosférica (exercida na superfície do líquido) com a pressão efetiva (pressão existente na profundidade h). Esse princípio descarta que a pressão existente em certo ponto do fluido dependa da geometria do recipiente do fluido.
Matematicamente, temos a Lei de Stevin como sendo:
Em que P é a pressão exercida sobre o corpo, P0 é a pressão atmosférica na superfície do líquido, que em geral é 1 atm (105Pa), e Pef é a pressão efetiva exercida pelo líquido no corpo.
Vamos demonstrar a seguir como a pressão existente em um corpo submerso em um líquido depende da densidade desse líquido e do seu deslocamento.
Demonstração
A pressão atmosférica na superfície do líquido é constante, P0 então não sofre alteração.
Todavia, a pressão efetiva sofre alteração conforme a profundidade do corpo se altera no líquido, assim, podemos escrever que:
Pela segunda Lei de Newton, temos que a força pode ser escrita pelo produto da massa pela aceleração, então:
A massa pode ser escrita em função da densidade como: m = d.V, assim:
O volume é definido como sendo o produto da área pela altura, e no caso do corpo submerso, ele está abandonado, ou seja, está sob a aceleração da gravidade, assim temos:
Simplificando, temos:
A equação (11) é a Lei de Stevin para qualquer fluido, seja ele líquido ou gasoso, desde que seja incompressível.
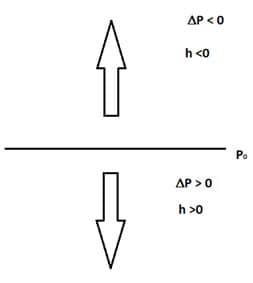
Nessa equação, consideramos a profundidade como medida positiva, ou seja, da superfície do líquido para baixo como deslocamento positivo, e a altura, ou seja, deslocamento para cima como negativo, isso porque a pressão diminui para quanto maior for a sua altura, e aumenta para quanto maior for a sua profundidade.
Ainda na equação (11), a densidade a ser considerada é a do fluido que envolve o corpo submerso, isso porque é o fluido que realiza a pressão sobre o corpo. Agora, vamos exemplificar:
Exemplo 7
A figura demonstra um corpo esférico submerso em água, cuja densidade é de 1000kg/m³.

O corpo esférico está a uma profundidade de 2 metros, e, na superfície, a pressão é de 1atm.
Neste caso, a pressão sobre o corpo esférico é de? (considere a aceleração da gravidade g = 10m/s²).
Solução:
Primeiramente, temos que estabelecer que 1atm = 105Pa, e em seguida aplicar a Lei de Stevin, assim:
Dividindo este resultando por 105Pa, podemos concluir que a pressão na água a 2 metros de profundidade é de:
Isso significa que a pressão a 2 metros de profundidade aumenta de 1atm para 1,2atm, ou seja, a um aumento de .
Mas e se considerarmos a profundidade de 3 metros?
Para a profundidade de 3 metros, houve um aumento de pressão de 0,3atm, ou seja, para cada 1 metro de profundidade, há um acréscimo de 0,1atm de pressão.
Isso mostra que a pressão determinada pela Lei de Stevin é uma função, a qual se comporta em função da profundidade, assim, a equação (11) é corretamente descrita por uma função, como demonstrado em (12):
Se observarmos, temos uma função afim, em que Po é o coeficiente linear, e o produto da densidade pela aceleração gravitacional (d.g) é o coeficiente angular da reta.
Então, para o caso de um corpo afundando no líquido, ou seja, para um corpo se deslocando cada vez mais para o fundo do líquido, a pressão aumenta linearmente, como mostra o gráfico.
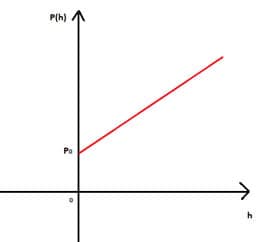
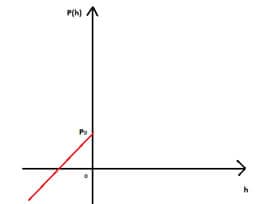
Porém, se ao invés de afundar, o corpo subir, como, por exemplo, um balão, a pressão diminui com o aumento da sua altitude, isso porque consideramos o posicionamento para cima como negativo.
Desta maneira, o gráfico da pressão por altura é representado no gráfico a seguir.
A figura seguinte demonstra a convenção de consideração da profundidade h com a variação de pressão
Princípio de Arquimedes
Você já deve ter se sentido mais leve ao entrar em uma piscina, ou ao mergulhar na água de um rio ou de alguma praia. Não se trata de uma simples impressão, isso ocorre graças à força de resistência aplicada pelo líquido a qualquer corpo que esteja totalmente ou parcialmente submerso. Essa força se chama empuxo, sendo representada pela letra E.

Essa força é descrita graças ao Princípio de Arquimedes.
Na íntegra, esse princípio diz que para todo corpo submerso ou parcialmente submerso existe uma força de direção vertical, cujo sentido é de baixo para cima, igual ao peso do volume do líquido deslocado pelo corpo.
Matematicamente, a força empuxo é dada como:
Na qual:
- d é a densidade do líquido
- g é a aceleração da gravidade local e
- V é o volume do líquido deslocado
O volume V do líquido deslocado é exatamente igual ao volume submerso do corpo sólido.
Exemplo 8
Considere que uma esfera de metal de 5cm de raio está completamente submersa e em repouso em um tanque com água salgada de 1,03g/cm³ de densidade. Considerando a aceleração gravitacional como 9,8m/s², qual o módulo, a direção e o sentido da força de empuxo atuante nesta esfera?
Veja a solução desta questão, que aborda o assunto Empuxo, no vídeo a seguir.
Módulo da força de empuxo
Exemplo 9
Considere uma esfera de 4kg de massa, que está afundando em um ambiente aquático cuja densidade é de 1001kg/m³.
Considerando a aceleração gravitacional como 10m/s², e o volume do corpo como 0,5x10-3m³, a aceleração com a qual esse corpo afunda é igual a:
Solução:
Primeiro, temos que analisar o corpo afundando.
Para baixo, temos a aceleração gravitacional; para cima, temos a força de empuxo, porém a resultante das forças não é nula.
Agora, existe um movimento acelerado para baixo:
Substituindo os valores do enunciado:
Ou seja, o corpo afunda neste líquido com uma aceleração de 8,75m/s².

Teoria na prática
Para estudo de densidade de líquidos imiscíveis, normalmente, utilizam-se vasos comunicantes.
Os vasos comunicantes são recipientes de líquidos em formato de U, que permitem que os líquidos fiquem em contato.
Para encontrar a densidade de um líquido desejado, utiliza-se um líquido cuja densidade é conhecida, e então aplica-se a Lei de Stevin.
Vejamos a situação do vaso comunicante que aparece na figura. A altura das duas colunas dos líquidos são proporcionais às suas densidades:
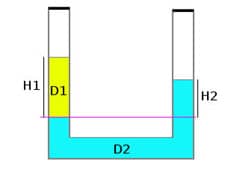
Vamos considerar que o líquido azul, de densidade d2, é a água do mar, com densidade de 1,03g/cm³, e que a altura H2 é de 10cm, e a altura H1 do líquido amarelo de densidade desconhecida é de 13cm.
Diante disso, vamos determinar a densidade do líquido 1:
Utilizando a Lei de Stevin, conseguimos determinar a densidade do líquido desconhecido, fazendo uma simples relação entre funções afins.
Mão na Massa
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Aplicar a equação da continuidade na dinâmica dos fluidos
Introdução
Você já parou para se perguntar por que quando queremos fazer uma mangueira jogar a água mais longe tapamos parte da saída com o dedo?
Fazemos isso instintivamente e sabemos que funciona, porém, o que explica esse fenômeno? A resposta é a equação da continuidade.
Princípio da continuidade
O que ocorre quando tapamos parte da saída da água na mangueira?

Nós diminuímos a área da seção transversal dela.
Isso aumenta a pressão interna na mangueira e, consequentemente, aumenta a velocidade de saída da água.
Como a velocidade da saída é maior, as moléculas de água são arremessadas para mais longe.
Com isso, conseguimos concluir que, quanto menor for a área de saída da água (sem bloqueá-la por completo), maior será a velocidade de saída da água e, por sua vez, maior será o alcance.
A esse fenômeno físico, damos o nome de continuidade, e matematicamente expressamos esse fenômeno pela equação da continuidade:
Demonstração
A equação da continuidade relaciona a velocidade de escoamento de um fluido com a área disponível para o escoamento.
Para compreender a matemática por trás desse fenômeno, vamos observar a figura:
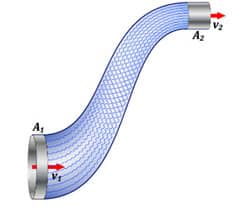
Nela podemos verificar que existem duas áreas de seção retas distintas, A1 e A2, em que A1 > A2.
Considere que em um intervalo de tempo (), certo volume () do fluido passa por A1.
Sendo esse fluido incompressível, podemos assumir que o mesmo volume (ΔV) sairá por A2, ou seja, o volume na área 1 (V1) é igual ao volume da área 2 (V2).
Durante o intervalo de tempo , o espaço percorrido pelo fluido é expresso pela equação da velocidade , sendo a velocidade de escoamento.
Assim, podemos escrever:
Os volumes V1 e V2 podem ser descritos em função das áreas e do deslocamento do fluido, tomando a área da seção reta da mangueira como a área da base e o deslocamento do fluido como a altura , assim, para os volumes V1 e V2:
Como vimos, da cinemática podemos escrever que , assim:
Esta é a equação (14) da continuidade e que relaciona a velocidade dos fluidos com a área de seção reta pela qual o volume do fluido atravessa.
Vamos verificar a sua utilidade:
Exemplo 10
Em uma mangueira de área de seção reta A, escoa certo volume V de água por segundo. Uma pessoa manipulando a mangueira tapa metade da área da saída com o dedo. Diante disso, qual é a nova velocidade da água ao abandonar a mangueira?
Veja a solução desta questão, que aborda o assunto Princípio da continuidade, no vídeo a seguir.
Velocidade de saída de um jato d´água de uma mangueira

Teoria na prática
Digamos que em uma mangueira de diâmetro de 2” (duas polegadas) atravessam 250mL de água por segundo.
Com essa área de seção reta e com a mangueira posicionada a uma angulação com a horizontal de 45°, a água possui um alcance horizontal de 4m (quatro metros).
Vamos então determinar o alcance do jato d’água para o caso da área da seção transversal da saída da mangueira ser reduzida, pela metade, por um terço e por um quarto da área da seção transversal inicial.

Sabemos da cinemática que, em x, a trajetória é retilínea e uniforme, ou seja, é um M.R.U. (Movimento Retilíneo Uniforme).
Assim, podemos escrever que o alcance em x é dado pela equação do M.R.U.:
Na qual:
- x(t) é a posição final
- x0 é a posição inicial
- v0x é a velocidade inicial na horizontal
- t é o tempo
O alcance (A) é determinado como sendo a variação da posição final do jato d’água, com a posição inicial:
Dessa maneira, podemos escrever que:
Porém, precisamos descobrir o que é esse .
Para isso, vamos olhar a figura e observar o triângulo retângulo formado entre os vetores v0, v0x e v0y
Como v0x é o cateto adjacente ao triângulo retângulo, podemos escrever que:
Assim, o alcance pode ser descrito como:
O alcance inicial é de 4 metros, e isso ocorre em 1 segundo, que é o tempo de vazão da mangueira:
Agora que conhecemos a velocidade inicial v0, vamos modelar uma equação de continuidade que nos permita possuir a velocidade do jato d’água, com a redução da área da seção reta:
A área da seção reta da mangueira é um círculo: . Assim:
Note que a velocidade final ficou em função da razão entre o raio inicial e final da saída de água ao quadrado.
Neste caso, como os raios operam matematicamente em uma razão, é necessário fazer a conversão de polegadas para metros, todavia temos que nos preocupar com o raio inicial r0, pois nos é dado o valor do diâmetro que é de 2”, assim, o raio é igual a 1”. Logo, continuando com nossa modelagem matemática, temos:
Montemos uma tabela para demonstrar os resultados das velocidades em m/s, das três situações pedidas no enunciado: (lembre-se de que r0 = 1” e que )
| Raio (“) | Velocidade (m/s) |
|---|---|
Vamos agora adaptar a equação do alcance deduzida acima(), para utilizar as velocidades determinadas na tabela anterior, assim:
Utilizando t = 1s, e as velocidades da tabela prévia, vamos montar uma nova tabela, com os novos alcances:
| Velocidade (m/s) | Alcance (m) |
|---|---|
Chegamos à conclusão de que o alcance aumenta com a diminuição da área da seção reta, porque a velocidade de lançamento também aumenta.
Mão na Massa
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 4
Aplicar a equação de Bernoulli na dinâmica dos fluidos
Introdução
A equação de Bernoulli descreve o comportamento de um fluido que se move ao longo de um tubo.
Para compreendê-la, vamos analisar a figura a seguir:
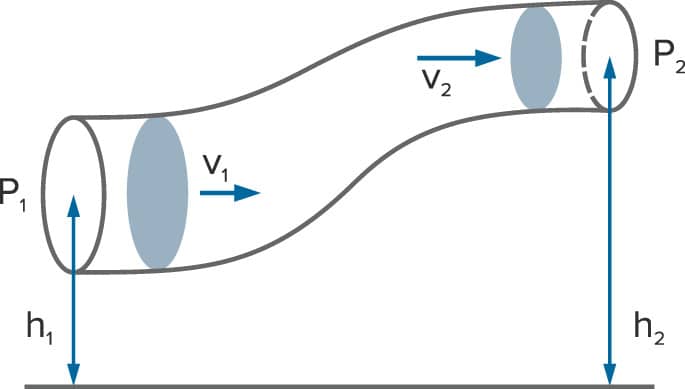
Equação de Bernoulli
O princípio de Bernoulli (princípio que origina a equação de Bernoulli) afirma que em um fluxo sem viscosidade há o aumento de velocidade do fluido, simultaneamente com uma diminuição de pressão, ou diminuição na energia potencial do fluido.
Para um fluido incompressível, a equação de Bernoulli possui a seguinte forma:
Na qual:
Três são as afirmações convencionadas que necessitam ser satisfeitas para que a equação se aplique:
Quando o líquido aumenta a sua velocidade, a pressão no tubo diminui, e isso é previsto pela equação de Bernoulli, por isso, esse fenômeno é chamado de Princípio de Bernoulli. Um fato curioso, é que esta equação foi deduzida e apresentada por Leonhard Euler.
Leonhard Euler (1707-1783) foi um matemático suíço criador da fórmula de Euler.
Vejamos como Euler deduziu tal equação:
Demonstração
Na figura, a seguir, observamos um tubo contínuo que apresenta um desnível de altura.
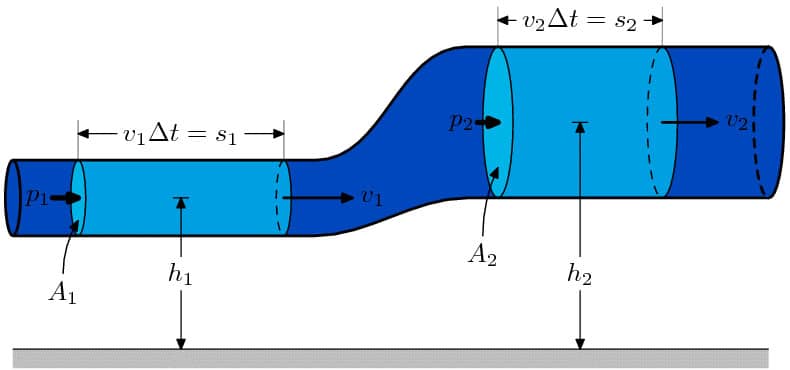
Euler utilizou o princípio da conservação da energia para afirmar que o trabalho (W) realizado pelo fluido é constante em todo o tubo, assim, pegando somente dois pontos do tubo:
Em que F1 e F2 são as forças aplicadas pelo fluido e s1 e s2 os deslocamentos sofridos pelo fluido.
Multiplicando e dividindo ambos os lados da equação pelas suas respectivas áreas e fazendo , temos:
Força dividida por área e pressão:
Assim, podemos dizer que:
Podemos afirmar também que a variação da energia potencial no tubo é igual a:
Fazendo V = A.s:
Podemos fazer , assim:
E, por fim, podemos afirmar que a variação da energia cinética do fluido escoando pelo cubo é:
Fazendo , temos:
Temos então que as equações (17), (18) e (19) correspondem à variação do trabalho, variação da energia potencial, e variação da energia cinética do fluido no interior do tubo, respectivamente.
Assumindo agora que a variação da energia cinética é igual à soma entre a variação do trabalho e a variação da energia potencial, temos:
Rearranjando, podemos escrever:
Podemos simplificar a equação, primeiramente, verificando que existem e d em todos os termos da equação. Todavia, vemos também que do lado esquerdo temos em todos os termos e do lado direito, .
O produto é a vazão do escoamento, sendo ela a mesma em todo o tubo, então podemos afirmar que , e também simplificar esses termos, assim temos:
Vamos verificar a aplicação da equação de Bernoulli:
Exemplo 11
Em um reservatório cilíndrico existe determinado fluido cuja altura no reservatório é h1. Um furo é realizado no reservatório a uma distância h2 da superfície do líquido, como mostra a figura seguinte.
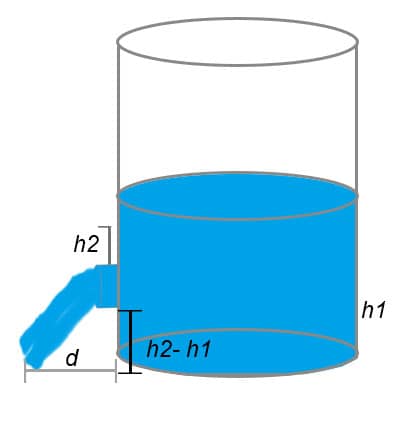
Determine a que distância d do reservatório o fluido tocará o solo:
Veja a solução desta questão, que aborda o assunto Equação de Bernoulli, no vídeo a seguir.
Distância de alcance de um jato d’água em função da pressão

Teoria na prática
Giovanni Battista Venturi criou um aparato, chamado de tubo de Venturi, para medir a velocidade de escoamento e vazão de um líquido incompressível através da variação da pressão sofrida pelo líquido durante a passagem deste por um tubo de diâmetro mais largo e depois por outro tubo de diâmetro mais estreito.
Giovanni Battista Venturi (1746-1822) foi um físico italiano descobridor do efeito Venturi e contemporâneo de Leonhard Euler.
Este aparato segue o Princípio de Bernoulli e o Princípio da continuidade.
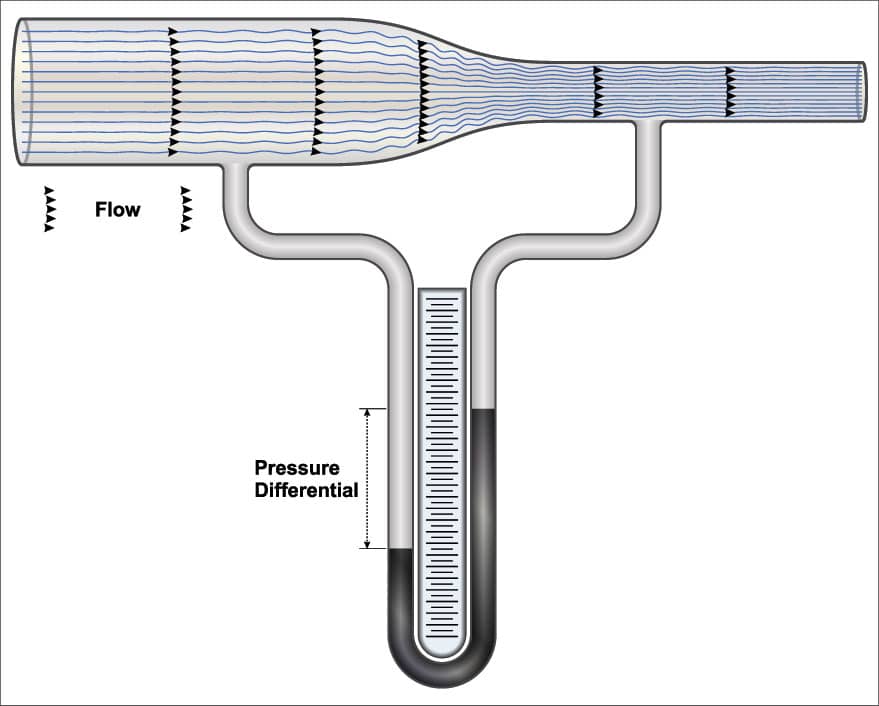
O tubo tem o seu funcionamento através da diferença existente entre as suas seções transversais.
É possível notar que, nesse equipamento, o diâmetro central do tubo é menor que o diâmetro das extremidades. Isso faz com que a velocidade do escoamento na região central do tubo seja muito maior do que nas extremidades, resultando em um menor campo de pressão devido à concentração de energia do sistema.
A diferença de altura do líquido no tubo em U registra a diferença de pressão existente no tubo de Venturi, e através dessa diferença de pressão, determinamos a velocidade e vazão do escoamento do fluido que atravessa esse tubo.
Afirmando que o tubo de Venturi não admite diferenças de elevação, escrevemos a equação de Bernoulli, da seguinte maneira:
Ao analisar a equação anterior, considerando que a região 1 possui maior área de seção reta e a região 2 possui a menor área de seção reta, podemos afirmar que para uma vazão constante, quanto menor for a área da seção reta, maior será a velocidade de escoamento.
Mão na Massa
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Vimos o conceito de pressão e densidade aplicado a fluidos.
Aprendemos como funcionam os macacos hidráulicos pelo Princípio de Pascal e como a profundidade pode influenciar na pressão hidrostática sobre um sólido através do Teorema de Stevin. Assimilamos, ainda, a técnica de medição de densidade de fluidos por meio do aparato chamado de vasos comunicantes.
Verificamos que, para um fluido em movimento, a medição da vazão é de suma importância.
Com a redução da área da seção reta de um tubo, há o aumento da velocidade do escoamento do fluido devido ao Princípio da continuidade das massas, que garante que a quantidade de massa de um fluido incompressível, que adentra em um tubo por segundo, é a mesma que o abandona.
Por fim, descobrimos que a equação de Bernoulli garante a continuidade de escoamento em um tubo, cujo fluido é incompressível.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Aplicou os conceitos de densidade, volume e pressão
Aplicou os conceitos de Arquimedes e Pascal na estática dos fluidos
Aplicou a equação da continuidade na dinâmica dos fluidos
Aplicou a equação de Bernoulli na dinâmica dos fluidos
