Descrição
As características construtivas das máquinas de corrente contínua, do comportamento dos geradores de corrente contínua e do comportamento dos motores de corrente contínua.
PROPÓSITO
Identificar as características construtivas das máquinas de corrente contínua e sua influência nas condições de operação para compreensão do funcionamento das máquinas de corrente contínua sob diferentes condições, considerando seu regime de funcionamento em regime permanente.
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos uma calculadora científica, a calculadora de seu smartphone/computador ou um software matemático que você conheça melhor.
OBJETIVOS
Módulo 1
Descrever as características construtivas dos geradores e motores de corrente contínua
Módulo 2
Examinar o funcionamento dos geradores de corrente contínua
Módulo 3
Analisar o funcionamento dos motores de corrente contínua
Geradores e motores de corrente contínua
MÓDULO 1
Descrever as características construtivas dos geradores e motores de corrente contínua
Introdução
As máquinas de corrente contínua (máquinas CC) são divididas em:
- Geradores de corrente contínua (geradores CC)
- Motores de corrente contínua (motores CC)
Os geradores CC convertem energia mecânica em energia elétrica e os motores CC convertem energia elétrica em energia mecânica.
No gerador CC, as tensões são induzidas por um condutor em movimento em uma região do espaço que possui uma densidade de campo magnético. Já os motores produzem trabalho útil a ser usado por uma carga acoplada ao seu eixo pelo princípio de força induzida em um condutor percorrido por corrente, imerso em uma região do espaço que possui uma densidade de campo magnético.
Para iniciarmos o entendimento dessas máquinas, vamos analisar a tensão induzida em uma espira que se localiza em uma região do espaço submetida a um campo magnético.
Tensão induzida em uma espira
Sabemos que uma tensão será induzida em um condutor, que é posto em movimento em uma região do espaço submetida a um campo magnético. Essa tensão é dada pela fórmula:
$$e_{ind}=\left(v\ \times\vec{B}\right).\vec{l}$$
(1)
O estudo da máquina linear permitiu compreender como ocorre o surgimento dessa tensão induzida. Porém, a máquina linear é uma máquina hipotética. Como tornar possível a aplicação das tensões induzidas?
Para iniciarmos a compreensão de como o gerador opera na prática, observe a Figura 1. Nela, pode-se ver uma espira imersa em uma região do espaço que possui uma densidade de campo magnético $$\vec{B}$$. Essa densidade de campo é produzida pelas faces (ou sapatas) polares norte e sul, identificadas por N e S, respectivamente.
O campo $$\vec{B}$$ sempre flui da face polar N para a face polar S, conforme mostra a figura. Uma espira encontra-se entre as faces polares e possui os segmentos: ab, bc, cd e da.
O início e o fim da espira são ligados a um dispositivo denominado anel coletor. Escovas de grafite fazem o contato elétrico com esses anéis coletores, levando para o meio externo a tensão induzida na espira.

Pela aplicação da Equação 1, verifica-se que as tensões nos segmentos bc e da serão iguais a zero. As tensões nos segmentos ab e cd, para a posição da espira indicada na figura, serão:
Segmento $$e_{ab}=\left(v\ \times\vec{B}\right).\vec{l\ }=vBL=\ \omega rBL$$, apontando no sentido indicado na figura.
Segmento cd: $$e_{cd}=\left(v\ \times\vec{B}\right).\vec{l\ }=vBL=\ \omega rBL$$, apontando no sentido indicado na figura.
Portanto, a tensão terminal Vt será $$2ωrBL$$.
Temos que destacar que a tensão induzida em todas as máquinas elétricas será sempre proporcional ao campo magnético ($$\vec{B}$$), à velocidade angular ($$\omega$$) e às suas caraterísticas construtivas (para esse caso, 2rL).
Na posição considerada na Figura 1, o ângulo formado entre o vetor velocidade e o vetor campo magnético formavam entre si 90°. Contudo, à medida que a espira rotaciona, os segmentos ab e cd passarão pelos pontos indicados na Figura 2 a seguir:

Percebe-se que, em cada um desses pontos, o ângulo entre vetor velocidade e o vetor densidade de campo magnético irá variar. Veja a forma de onda da tensão terminal ao longo de uma rotação:

Vimos que a tensão é senoidal, uma vez que o ângulo entre os vetores velocidade e campo magnético varia ao longo de uma rotação. Para produzir uma tensão contínua ao longo de toda uma rotação, a solução empregada é tornar as faces polares côncavas. Dessa forma, as linhas de campo serão sempre perpendiculares ao vetor velocidade da espira, conforme apresentado abaixo:

Essa nova configuração das faces polares resolve o problema da variação da tensão induzida ao longo da rotação da espira. Entretanto, a tensão induzida continua invertendo a sua polaridade quando os segmentos trocam de faces polares:

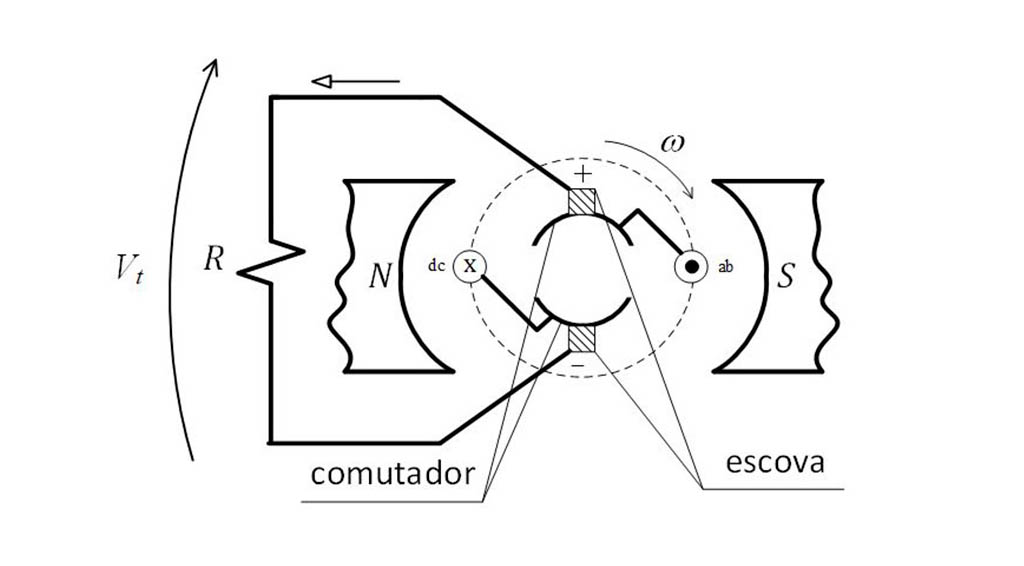
Agora, para eliminar o semiciclo negativo da tensão terminal, a máquina CC emprega um dispositivo denominado “comutador”. Cada terminal da espira é conectado a um comutador e a tensão induzida é levada aos terminais da máquina por meio das escovas. Repare que, quando um lado da espira muda de face polar, uma nova escova passa a fazer a sua conexão com o meio externo, garantindo que a tensão permaneça constante. A figura a seguir mostra o comutador na máquina CC:

Vejamos agora o sentido da tensão induzida nos segmentos das espiras dc e ab. Observe que cada comutador está conectado a um extremo da espira e que ele gira solidário ao eixo do rotor. Portanto, à medida que o rotor gira, a escova ( + ) sempre estará conectada ao terminal da espira, que se move sob a face polar sul, enquanto a escova ( - ) sempre estará conectada ao terminal da espira sob a face polar norte.
A tensão terminal do gerador nesse novo arranjo da máquina é mostrada na forma de onda na Figura 8:

Seria um desperdício, porém, empregar um rotor apenas com uma espira. De modo a aproveitar todo o rotor, são adicionadas espiras ao rotor e estas são conectadas entre si por meio dos comutadores, conforme mostrado na Figura 9:

Agora, qual é a tensão terminal obtida no gerador para o instante representado na figura? Para determinar esse valor, vamos sair da escova x até chegar à escova y.
Antes, vamos convencionar que o início da bobina 1 será chamado simplesmente de 1 e o seu final, por 1’. Essa convenção valerá também para as bobinas 2, 3 e 4.
Primeiro, vamos fazer esse caminho pela espira 1. Saindo da escova x, chegamos ao comutador a, que está ligado a 1. O terminal 1’ está ligado ao comutador b, que está ligado a 2. O terminal 2’ está ligado ao comutador c, que finalmente chega à escova y.

Em azul, na Figura 10, podemos ver o caminho feito pela corrente pelo terminal 1 e 2.
Agora, vamos fazer esse caminho pela espira 4. Saindo da escova x, chegamos ao comutador a, que está ligado a 4’. O terminal 4 está ligado ao comutador d, que está ligado a 3’. O terminal 3 está ligado ao comutador c, que finalmente chega à escova y.
Portanto, a tensão terminal será 4e e o circuito equivalente para o instante de tempo apresentado na Figura 9 é mostrado na Figura 10.

Considere agora que o rotor tenha girado no sentido anti-horário e agora esteja na posição indicada na Figura 12. Prove que a tensão terminal Vt será 2e.

Como resultado da adição de mais espiras no gerador, a forma de onda da tensão terminal é indicada a seguir:

Na análise das Figuras 10 e 11, percebemos que existem dois caminhos paralelos entre as escovas x e y. O número de caminhos paralelos é dado pelo número de polos. Ou seja, uma máquina de dois polos terá dois caminhos paralelos, máquina de quatro polos terá quatro caminhos paralelos e, assim, sucessivamente.
Em cada um dos caminhos existem 4 condutores, perfazendo um total de oito condutores na máquina. Dá-se o nome de condutores aos segmentos das espiras, nos quais pode ser induzida a tensão (por exemplo, os segmentos ab e cd da Figura 1). Diante do exposto, podemos constatar que a tensão induzida do gerador será dada por:
$$E_a=\frac{Z}{a}\varpi rBL$$
(2)
Considerando que a densidade de fluxo, por ser calculada pelo fluxo total dividida pela área do polo, temos:
$$B=\frac{\phi}{A_p}$$
(3)
Em que:
- Ap é a área do polo
Portanto:
$$A_p=\frac{2\pi rL}{P}$$
(4)
Em que P é o número de polos.
Agora, substituindo a Equação 4 em 2, temos:
$$E_a=\frac{Z}{a}\varpi r\frac{\phi}{\frac{2\pi rL}{P}}L$$
(5)
Rearranjando a expressão, teremos:
$$E_a=\left(\frac{ZP}{2\pi a}\right)\varpi\phi=k_1\varpi\phi$$
(6)
Como já visto, a tensão induzida na máquina depende das características construtivas, da velocidade angular e do fluxo. Como normalmente a velocidade da máquina é dada em rotações por minuto (rpm), podemos fazer:
$$k=k_1\frac{2\pi}{60}=\frac{ZP}{60a}$$
(7)
E finalmente chegamos a:
$$E_a=kn\phi$$
(8)
Problemas da comutação
Suponha que, inicialmente, não haja carga conectada aos terminais do gerador (máquina operando em vazio). Teremos somente a tensão induzida nos terminais da máquina. Como não há corrente, a própria tensão induzida será a tensão terminal da máquina.
Nessa situação, as espiras que se encontram entre as faces polares não possuem tensões induzidas, pois estão na região denominada plano magnético neutro, conforme a Figura 14. Observe que o plano magnético neutro é 90° adiantado do campo resultante no interior do estator, que no momento é o campo B.

Agora, quando uma carga é conectada aos terminais do gerador, uma corrente passa a circular nas espiras do rotor. Essa corrente é denominada “corrente de armadura” e sua circulação nas espiras do rotor faz surgir um campo de reação de armadura BRA, veja:

O campo resultante no interior do estator e o novo plano magnético neutro são apresentados na figura seguinte. Por que o deslocamento do plano magnético neutro é um problema?

A comutação das máquinas ocorre quando a tensão nos condutores curto-circuitados é zero. Porém, o deslocamento do plano magnético neutro faz com que nessa região do espaço passe a ter um fluxo diferente de zero, ou seja, no momento da comutação, a tensão dos condutores na zona interpolar não será zero. Isso provocará:
- Centelhamento
- Desgaste nas escovas
- Desgaste no comutador
- Necessidade de maior manutenção
Existem duas formas de resolver o problema do deslocamento do plano magnético neutro. A primeira é mudar o ponto de comutação das escovas. No entanto, essa solução não é a mais viável porque implicaria um ajuste diferente para cada corrente.
O segundo método é usar o enrolamento de interpolos, que são pequenos polos localizados nas regiões interpolares, cuja função é produzir um campo magnético proporcional à corrente de armadura. Para que isso ocorra eles deverão ser percorridos pela corrente de armadura da máquina. Veja o enrolamento de interpolos representado a seguir:

Além do deslocamento do plano magnético neutro, a comutação provoca um enfraquecimento do fluxo no interior da máquina, produzindo queda da tensão induzida nos geradores e aumentos indesejáveis na velocidade dos motores.
Para solucionar esse problema são empregados os enrolamentos compensadores. Eles são construídos de tal forma que produzem um fluxo contrário ao fluxo de reação de armadura. Para obter tal resultado, o enrolamento de compensação é construído nas faces polares, conforme apresentado a seguir:

Curva de magnetização de um gerador CC
A curva de magnetização relaciona a tensão terminal em vazio com a corrente de campo. Para obter-se essa curva, o gerador é posto a rotacionar em velocidade constante em vazio (sem nenhuma carga conectada em seus terminais).
Inicialmente, a corrente de campo é ajustada para zero e a tensão induzida residual do gerador é medida. Em seguida, a corrente de campo é aumentada gradativamente e, para cada valor de corrente, a tensão induzida é medida. A corrente de campo é aumentada até chegarmos ao ponto de saturação da máquina, ou seja, mesmo com o aumento da corrente de campo a tensão induzida não é mais aumentada.
Como não há corrente de armadura, a tensão terminal da máquina será a própria tensão induzida. A curva de magnetização típica de um gerador é mostrada a seguir:

Agora, suponha que você tenha a curva de magnetização para dada velocidade n1. Como determinar a tensão induzida para o gerador quando este é posto a rotacionar em uma velocidade n2 > n1?

Da Equação 8, sabemos que a tensão induzida é proporcional às características construtivas da máquina, à sua velocidade e ao fluxo:
$$E_a=kn\phi$$
(8)
Então, a tensão induzida para a velocidade n1 e para a velocidade será:
$$E_{a1}=kn_1\phi$$
(9)
Mantendo-se o fluxo constante para as duas velocidades, teremos que a tensão induzida para a velocidade n2 será:
$$E_{a2}=kn_2\phi$$
(10)
Portanto, a tensão induzida para a velocidade n2 será:
$$\frac{E_{a1}}{n_1}=\frac{E_{a2}}{n_2}$$
(11)
Mão na Massa

Teoria na prática
Uma pequena indústria utiliza um gerador hipotético cuja tensão induzida no rotor é igual a 100 V. Escovas fazem o contato elétrico entre o comutador desse gerador e seus terminais onde encontra-se conectado um resistor de 10 $$\Omega$$. Considerando que a queda de tensão nas escovas seja 2 V, determine a potência total dissipada nelas.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Examinar o funcionamento dos geradores de corrente contínua
Introdução
Geradores são máquinas que convertem energia mecânica em energia elétrica. Os geradores CC são classificados de acordo com sua forma de excitação, ou seja, a forma como é gerada a densidade de campo necessária para gerar a tensão induzida. Os tipos de geradores de corrente contínua são:
- Com excitação independente
- Shunt
- Série
- Composto aditivo:
- Curto
- Longo
- Composto subtrativo:
- Curto
- Longo
Gerador com excitação independente
Como o próprio nome diz, a excitação de um gerador com excitação independente é formada por um circuito CC com fonte própria de tensão (Figura 20) em que:
- Vf é a tensão de campo
- Rf é resistência do enrolamento de campo
- Raj é a resistência de ajuste para o controle da corrente de campo
- If é a corrente de campo
- Nf é o número de espiras do circuito de campo
- Ea é a tensão induzida
- Ra é a resistência de armadura
- Vt é a tensão terminal
- If é a corrente de campo
- Ia é a corrente de armadura
- IL é a corrente de carga

Caso o gerador possua enrolamentos de compensação e de interpolos, teremos ainda:
- Rc é a resistência do enrolamento de compensação
- Ri é a resistência do enrolamento de interpolos
Caso a queda de tensão das escovas não seja desprezível, teremos:
- $$\Delta$$Vesc é a queda de tensão nas escovas
Para esse gerador temos as seguintes equações:
- $$I_a=I_L$$
- $$V_f={(R_{aj}+R_f)I}_f$$
- $${R_F=R}_{aj}+R_f$$
- $$V_t={E_a-(R_a+R_i+R_c)I}_a-\Delta V_{esc}$$
- $$E_a=kn\phi$$
A força magnetomotriz da bobina de campo é:
$$\mathcal{F}_{mm}=N_fI_f-\ \mathcal{F}_{mmra}$$
(12)
Em que:
- $$\mathcal{F}_{mmra}$$ é a força magnetomotriz de reação de armadura (para as máquinas que não possuem enrolamento de compensação).
O que buscamos em todo gerador é identificar a sua característica terminal, ou seja, a relação entre a sua tensão terminal em função da corrente de carga solicitada.
Considere um gerador com enrolamento de compensação. Se esse gerador é acionado com velocidade constante e se sua corrente de campo é mantida constante, a sua tensão induzida será constante e, desprezando-se a queda de tensão nas escovas, a tensão terminal do gerador será igual a:
$$V_t={E_a-(R_a+R_i+R_c)I}_a$$
(13)
Seu gráfico é:

Agora, supondo que a máquina não possua enrolamento de compensação, à medida que a corrente de carga aumenta, o fluxo de reação de armadura fará com que a tensão induzida diminua. Quanto menor a tensão induzida, maior será a queda da tensão terminal.
A característica terminal do gerador com excitação independente, sem enrolamento de compensação, possui queda de tensão mais acentuada do que a do gerador que possui enrolamento de compensação:

Outra característica importante a se definir sobre um gerador é a sua regulação de tensão, que nos diz em quanto a tensão terminal de um gerador aumentará caso seja retirada a carga conectada aos seus terminais. Usualmente, exprime-se a regulação em um valor percentual, que é dado por:
$${Reg}_\%=\frac{V_{t\;em\;vazio}-V_{t\;com\;carga}}{V_{t\;com\;carga}}100\%$$
(14)
O controle da tensão terminal do gerador com excitação independente pode ser feito por meio do controle da velocidade ou da corrente de campo, variando-se $$R_{aj}$$.
Gerador Shunt
A principal característica do gerador shunt é que o enrolamento de campo está conectado em paralelo com o circuito de armadura. Dessa forma, a tensão de campo será a própria tensão terminal do gerador.
Essa configuração traz a vantagem de não necessitar de uma fonte externa de tensão para operar o gerador.

Para este gerador temos as seguintes equações:
- $$I_a=I_L+I_f$$
- $$V_t={E_a-(R_a+R_i+R_c)I}_a$$
- $${R_F=R}_{aj}+R_f$$
- $$I_f={\frac{V_t}{R_F}}$$
- $$\mathcal{F}_{mm}=N_fI_f-\ \mathcal{F}_{mmra}$$
- $$E_a=kn\phi$$
Como é possível obter uma tensão terminal shunt sem possuir uma fonte externa de tensão?
O processo de obtenção da tensão terminal do gerador shunt é chamado de “autoexcitação”. Para que isso ocorra, a máquina deve possuir magnetismo residual. O processo de autoexcitação ocorre da seguinte forma:
Acionando-se o gerador, o magnetismo residual fará com que tenhamos uma tensão induzida residual, devido ao magnetismo residual da máquina, que será dada por:
$$E_{a\_residual}=kn\phi_{residual}%$$
(15)
Essa tensão residual fará circular uma corrente que gerará um fluxo, que se somará ao fluxo residual. Esse novo fluxo aumentará a tensão induzida que, por sua vez, aumentará a corrente no circuito.
Tal processo ocorrerá em ciclos até que a máquina atinja o ponto de operação em vazio:

Quais os fatores que impedem a autoexcitação?
A autoexcitação não ocorrerá quando:
- A máquina não possuir magnetismo residual;
- O circuito de campo estiver aberto;
- Polaridade da bobina de campo estiver invertida (campo inicial opõe-se ao magnetismo residual);
- Circuito de armadura estiver aberto;
- Houver mau contato entre as escovas e o comutador;
- A resistência de campo for maior que a resistência crítica.
Houver resistência de campo maior do que a resistência crítica.
Na reta Vt x If, da Figura 25, verifica-se que a declividade angular da reta é o valor de $$R_{aj}+R_f$$. Acontece que, à medida que aumentamos o valor de $$R_{aj}$$ a declividade da reta também vai aumentando até que, para determinado valor de resistência, não ocorrerá a autoexcitação da máquina. A essa resistência é dado o nome de resistência crítica. Veja:

A característica terminal do gerador shunt possui uma queda de tensão mais acentuado do que a do gerador com excitação independente. À medida que a corrente de carga aumenta, ocorre aumento da queda de tensão na resistência de armadura, que produz diminuição da tensão terminal, que reduz a corrente de campo, diminuindo a tensão induzida, reduzindo ainda mais a tensão terminal.
Veja o comportamento da caraterística terminal do gerador shunt:

O controle da tensão terminal do gerador shunt pode ser feito por meio do controle da velocidade ou da corrente de campo, variando-se $$R_{aj}$$.
Somente é possível determinar a tensão terminal do gerador shunt por meio da análise gráfica, que será apresentada a seguir:
- Tensão terminal com gerador shunt sem reação de armadura.
Como em condições nominais de operação, a corrente de campo é muito menor do que a corrente de carga, pode-se considerar que a corrente de armadura seja aproximadamente igual à corrente de carga.
É preciso fazer um segmento de reta ab cuja dimensão é a queda de tensão na resistência de armadura [volts], e esse segmento dever ser encaixado entre as curvas de Vt x If e Ea x If . Então, a extremidade a do segmento indicará o valor da tensão induzida e a extremidade b do segmento indicará o valor da tensão terminal:

- Tensão terminal com gerador shunt com reação de armadura.
Agora, além de acrescentar o segmento ab que representa a queda de tensão na resistência de armadura, devemos representar o efeito da redução do campo devido à reação de armadura. Para obter esse efeito, considere a expressão a seguir:
$$\mathcal{F}_{mm}=N_fI_f-\ \mathcal{F}_{mmra}$$
(16)
Reescrevendo esta equação da seguinte forma:
$$N_f{I_f}^\ast=N_fI_f-\ \mathcal{F}_{mmra}$$
(17)
Dividindo todos os termos da Equação 3-1 por Nf, temos
$${I_f}^\ast=I_f-\ \frac{\mathcal{F}_{mmra}}{N_f}$$
(18)
- $$I_f$$ é a corrente que passa pelo circuito de campo;
- $$\frac{\mathcal{F}_{mmra}}{N_f}$$ emula a redução de corrente da corrente principal que provoca a redução do campo magnético da máquina devido ao efeito de reação de armadura;
- $${I_f}^\ast$$ é a corrente resultante, que simula o campo a menor devido ao efeito de reação de armadura
Ou seja, a Equação 19 busca determinar um valor de $${I_f}^\ast$$, que seria uma corrente fictícia responsável por produzir o campo magnético reduzido no gerador shunt, em virtude do efeito da reação de armadura.
Para aplicar esse conceito na análise gráfica do gerador shunt, agora temos um segmento de reta bc, cuja dimensão é $$\frac{\mathcal{F}_{mmra}}{N_f}$$ [A]. Esse segmento será conectado ao segmento ab, e a tensão terminal será obtida conforme a Figura 29:

Gerador série
Os geradores CC série possuem o circuito de campo em série com o circuito de armadura, conforme mostra a figura a seguir:

Para este gerador temos as seguintes equações:
- $$I_a=I_L=I_s$$
- $$V_t={E_a-(R_a+R_{cs})I}_a$$
- $$\mathcal{F}_{mm}=N_sI_s-\ \mathcal{F}_{mmra}$$
- $$E_a=kn\phi$$
Quando esse gerador é acionado com velocidade nominal e sem carga conectada a seus terminais, não existe a corrente de armadura. Portanto, a tensão terminal da máquina será devida somente ao magnetismo residual. A partir do momento em que uma carga é aplicada ao gerador, o aumento do fluxo fará com que haja aumento da tensão induzida.
Inicialmente, esse aumento da tensão induzida em função do aumento da corrente de campo é maior do que a queda da tensão na resistência de armadura. Assim, a tendência é de aumento da tensão terminal. Porém, à medida que o material ferromagnético das faces polares entra em saturação, o aumento da corrente de armadura não provocará o aumento da tensão induzida e a queda de tensão na resistência de armadura continuará aumentando.
Agora, o efeito da queda de tensão na resistência de armadura sobrepujará o aumento da tensão induzida e a tensão terminal da máquina sofrerá redução, conforme pode ser visto:

Quando a máquina possui reação de armadura, o efeito da queda de tensão terminal com o aumento da corrente de carga é ainda mais acentuado:

Gerador composto
Os geradores compostos possuem os campos série e shunt, ou seja, a tensão induzida gerada é o resultado das forças magnetomotrizes dos campos shunt ($$N_fI_f$$) e do campo série ($$N_sI_s$$).
Normalmente, o efeito da força magnetomotriz do campo shunt é maior do que o campo série.
Os geradores compostos são classificados em:
Compostos aditivos: são aqueles em que a força magnetomotriz do campo shunt soma-se à força magnetomotriz do campo série. Os geradores aditivos são divididos em:
- Longos
- Curtos
Compostos subtrativos: são aqueles em que a força magnetomotriz do campo shunt subtrai-se à força magnetomotriz do campo série. Os geradores subtrativos são divididos em:
- Longos
- Curtos
Para se determinar se o efeito dos campos será aditivo ou subtrativo, usamos a mesma convenção dos transformadores. Correntes entrando no ponto das bobinas produzem um efeito aditivo das forças magnetomotrizes dos campos shunt e série:

Se temos em uma bobina a corrente entrando no ponto, e no outro a corrente saindo do ponto, essas correntes produzem um efeito subtrativo das forças magnetomotrizes dos campos shunt e série:

Nesses geradores, a força magnetromotriz é dada por:
(19)
Na Equação 19, emprega-se na força magnetomotriz do campo série o sinal:
- Positivo para o gerador aditivo
- Negativo para o gerador subtrativo
Em ambas as situações, a força magnetomotriz de reação de armadura reduz o campo resultante.
Da mesma forma como feito para o gerador shunt, podemos determinar uma corrente de campo equivalente, que é dada por:
(20)
Para compreender a característica terminal do gerador composto, é necessário entender a interação entre os efeitos dos campos shunt e série da máquina. Considere que a corrente de carga aumente, então a corrente de armadura aumentará. Nesse ponto, duas coisas poderão ocorrer:
1) Como a corrente de armadura aumenta, a queda de tensão na resistência de armadura aumentará, o que provocará aumento da tensão terminal.
2) O aumento de corrente de armadura também provocará aumento da força magnetomotriz do campo série, o que vai ocasionar o aumento da tensão induzida do gerador e, consequentemente, aumento da tensão terminal da máquina.
Esses dois efeitos são concorrentes. O primeiro provoca redução da tensão terminal e o segundo provoca o aumento da tensão terminal.
Agora, qual deles prevalecerá?
Gerador com poucas espiras no campo série:
A contribuição da força magnetomotriz do campo série é pequena. A tensão terminal cairá, mas de maneira menos acentuada do que no gerador shunt. Neste caso, dizemos que o gerador é hipocomposto.
Gerador com um pouco mais de espiras no campo série:
Nesse caso, no início, a contribuição do campo série supera o efeito da queda de tensão da resistência de armadura. Dessa forma, a tensão terminal aumenta. A partir de determinado ponto, a saturação começará a ter maior influência e, desse modo, a tensão terminal começará a cair. Nesse tipo de gerador, quanto a tensão terminal a plena carga é igual à tensão terminal em vazio, ele é dito ser do tipo plano.
Gerador com maior número de espiras no campo série:
A contribuição do campo série predomina sobre a queda de tensão na resistência de armadura e sobre o efeito de reação de armadura por um longo tempo. Nesse tipo de gerador, quanto a tensão terminal a plena carga é maior do que a tensão terminal em vazio, ele é dito ser do tipo hipercomposto.
Veja cada um dos tipos das características terminais do gerador composto:

Nos geradores subtrativos, o enfeito enfraquecedor da força magnetomotriz do campo série provoca uma redução ainda maior na tensão terminal, ocasionando queda de tensão terminal mais acentuada do que no gerador shunt.
Na prática, o gerador composto possui um número fixo de espiras no campo série. Com a adição de um reostato em paralelo com o campo série, ele é capaz de trabalhar com as diferentes características terminais. Então, com devido ajuste do reostato, o gerador pode trabalhar com as características terminais de shunt, hipocomposto, plano ou hipercomposto. Veja a exemplificação do circuito dessa configuração:

É necessário realizar a análise gráfica do gerador para determinar a tensão terminal do gerador em função de sua corrente de carga.
Para realizar a análise gráfica, observe a seguinte equação:
(21)
Vamos reescrevê-la da seguinte forma:
$${I_f}^\ast=I_f+I_{eq}$$
(22)
Em que:
(23)
Observe que, se o $$I_{eq}$$ < 0, a análise gráfica do gerador composto ficará igual à análise feita para o gerador shunt.

Agora, se $$I_{eq}$$ > 0, a análise gráfica será realizada da seguinte forma: o ponto a do segmento ab deverá estar posicionado na curva Ea x If, enquanto o ponto c do segmento bc deverá estar na reta Vt x Ef, conforme a figura:

Mão na Massa
Considere a curva de magnetização apresentada a seguir, levantada a 1800 rpm, para a resolução dos exercícios deste módulo.


Teoria na prática
Você vai dimensionar um gerador CC com excitação independente para alimentar as cargas de uma instalação fabril hipotética. As potências das cargas P1 e P2 valem, respectivamente, 2000 W e 1500 W. Sabendo que a tensão terminal das cargas deve ser mantida em 120 V e que o gerador é acionado em 1800 rpm, determine se ele conseguirá atender às cargas da instalação.
Dados:
- Raj = 0 a 40 $$\Omega$$
- Rf = 15 $$\Omega$$
- Vf = 120 V
- Ra = 0,40 $$\Omega$$
A potência total do sistema é: 3500 W
Resultando em uma corrente de 3500 / 120 = 29,16 A.
A tensão induzida será:
$$E_a=120+0,4\times29,16=131,66\;V\;a\;1800\;rpm$$
A corrente de campo será: $$I_f=5,25$$
O que resultará em:
$$R_{aj}=\frac{120}{5,25}-15=7,85\ \Omega$$
Para atender às condições impostas, a resistência de ajuste deverá ser de 7,85 $$\Omega$$
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Analisar o funcionamento dos motores de corrente contínua
Introdução
Motores e geradores são fundamentalmente a mesma máquina. O que diferencia uma da outra é o fluxo de energia. Motores são máquinas que convertem energia elétrica em energia mecânica.
Historicamente, os motores dc eram mais usados por propiciarem melhor controle de velocidade, mas, atualmente, a partir do advento da eletrônica de estado sólido, os motores vêm perdendo espaço para os motores de corrente alternada.
Em todo o estudo dos motores dc, será considerado que os motores serão alimentados por uma tensão contínua constante.
Os motores CC são classificados de acordo com sua forma de excitação, ou seja, a forma como é gerada a densidade de campo necessária para gerar a tensão induzida. Os tipos de motores de corrente contínua são:
- Com excitação independente (shunt)
- Série
- Composto aditivo:
- Curto
- Longo
- Composto subtrativo:
- Curto
- Longo
Princípio de funcionamento
Considere a máquina parada. Nesse momento, alimenta-se o circuito de campo, criando-se o fluxo. Em seguida, alimenta-se o motor com tensão terminal constante. A partir daí, circulará uma corrente de armadura, cujo valor será:
$$I_{A_{partida}}=\frac{V_t}{R_a}$$
(24)
Como no momento da partida a velocidade do rotor é zero, a tensão induzida no rotor será zero, ou um valor bem pequeno, caso a máquina possua magnetismo residual.
Cada um dos condutores da armadura será percorrido pela corrente:
$$i_{caminho}=\frac{I_{A_{partida}}}{a}$$
(25)
Nesses condutores, aparecerá uma força induzida:
$$F_{ind}=iBL$$
(26)
E um torque induzido dado por:
$$\tau_{ind}=\left(iBL\right)r$$
(27)
Analisando a Equação 27, verifica-se que o torque elétrico induzido na máquina é proporcional às suas características construtivas, ao fluxo e à corrente de armadura.
$$\tau_{ele}=k\phi I_A$$
(28)
Esse conjugado fará o rotor entrar em movimento. A partir do momento em que a máquina entra em movimento, uma tensão será induzida na armadura, já que:
$$E_a=kn\phi$$
(29)
A corrente inicial irá diminuir para um valor dado por:
$$I_{A_{partida}}=\frac{V_t-E_a\ }{R_a}$$
(30)
Teremos um processo de acomodação no qual a velocidade da máquina aumentará, provocando aumento da tensão induzida e, consequentemente, redução da corrente de armadura.
De maneira semelhante à máquina linear, o sistema entrará em equilíbrio, ou seja, sua velocidade será constante, quando o torque elétrico induzido for igual à soma do torque mecânico e do torque de perdas da máquina, conforme a equação a seguir:
$$\tau_{ele}=\tau_{mec}+\tau_{perdas}$$
(31)
Considere que, após entrar em regime, haja um aumento do torque mecânico do motor. Então:
$$\tau_{ele}<\tau_{mec}+\tau_{perdas}$$
(32)
Dessa forma, o motor diminuirá a velocidade e, consequentemente, a tensão induzida diminuirá. Como a tensão terminal do motor é constante, a corrente de armadura aumentará, aumentando o torque elétrico do motor. O motor entrará em equilíbrio quando novamente tivermos:
$$\tau_{ele}=\tau_{mec}+\tau_{perdas}$$
(33)
Porém, nessa nova situação, o motor entrará em equilíbrio em velocidade menor do que a original e com uma corrente de armadura maior do que a original.
Agora, analise qualitativamente o comportamento do motor quando há diminuição do torque mecânico.
Motor com excitação independente (motor shunt)
Como o próprio nome diz, a excitação de um motor com excitação independente é formada por um circuito CC com fonte própria de tensão, conforme mostra a figura:

Em função da consideração feita no sentido de que a tensão terminal do motor é mantida constante, o motor com excitação independente é igual ao motor shunt:

Para este motor temos as seguintes equações:
- $$I_a=I_L$$
- $$V_f={(R_{aj}+R_f)I}_f$$
- $${R_F=R}_{aj}+R_f$$
- $$V_t={E_a+(R_a+R_i+R_c)I}_a$$
- $$E_a=kn\phi$$
- $$\tau_{ele}=k\phi I_A$$
No gerador, estávamos interessados em determinar o comportamento da tensão terminal em função da variação de carga.
No motor, estamos interessados em determinar a velocidade de seu eixo em função da variação do torque mecânico aplicado ao motor, a curva $$ \omega_m\times \tau_{ele}$$ conforme a figura:

Ou seja, nos motores estamos interessados em determinar $$\omega_m(\tau_{ele})$$. Para se obter essa relação, sabemos que:
$$V_t={E_a+R_aI}_a$$
(34)
No entanto, como:
$$I_A=\frac{\tau_{ele}}{k\phi}$$ e $$E_a=kn\phi$$
(35)
Substituindo-se os valores anteriores na expressão tensão terminal, teremos:
$$V_t=kn\phi+R_a\frac{\tau_{ele}}{k\phi}$$
(36)
Resolvendo para n, teremos:
$$n=\ \frac{V_t}{k\phi}-R_a\frac{\tau_{ele}}{\left(k\phi\right)^2}$$
(37)
Considerando que a tensão terminal, k, o fluxo e a resistência de ajuste sejam constantes, a Equação 37 é a equação de uma reta (motor shunt).
Suponha agora que o motor não possua enrolamento de compensação. Assim, a medida que há um aumento da corrente de armadura, a tensão induzida diminuirá, aumentando a corrente de armadura, aumentando o torque induzido, aumentando a velocidade do motor, conforme mostra a Figura 43.

Um parâmetro importante para se conhecer do motor é a sua regulação de velocidade, que é dada por:
$${Reg}_\%=\frac{n_{\;em\;vazio}-n_{\;com\;carga}}{n_{\;com\;carga}}100\%$$
(38)
Analisando a Equação 37, verifica-se que existem três formas de se controlar a velocidade do motor:
1) Por meio da variação do fluxo
2) Por meio da variação da tensão aplicada à armadura
3) Inserindo-se resistências em série com a armadura
Inserindo-se resistências em série com a armadura
Controle da velocidade por meio da variação do fluxo
Suponha que a resistência de ajuste tenha aumentado. Nessa nova condição, a corrente de campo diminui, produzindo redução do fluxo e provocando redução da tensão induzida. A diminuição da tensão induzida provocará aumento da corrente, que por sua vez aumenta o torque da máquina. Ou seja, o aumento da resistência de ajusta provoca aumento da velocidade do motor.
Controle da velocidade por meio da variação da tensão aplicada à armadura
Nesse tipo de controle, a tensão terminal permanece constante e a tensão aplicada ao circuito de armadura é ajustada por meio de um circuito de controle:

Suponha que a tensão aplicada ao circuito de armadura aumente. O aumento da tensão aplicada aumenta a corrente de armadura, que por sua vez aumenta o torque elétrico do motor, aumentando a velocidade do rotor. Ou seja, o aumento da tensão da armadura provoca aumento da velocidade do motor.
Controle da velocidade por meio da inserção de resistência no circuito de armadura
Nesse tipo de controle insere-se uma resistência em série com o circuito de armadura, conforme mostra a Figura 44 – Controle de tensão por meio da inserção de resistência no circuito de armadura. O aumento da resistência diminui a corrente de armadura, que por sua vez reduz o torque elétrico, provocando diminuição da velocidade.

Motor série
O motor CC série possui o circuito de campo composto por poucas espiras em série com o circuito de armadura:

Enquanto não chega ao ponto de saturação da curva de magnetização, o fluxo magnético de um motor CC série é proporcional à corrente de armadura.
Supondo que haja um aumento da carga do motor, o fluxo aumentará, provocando o aumento da tensão induzida, que por sua vez produzirá diminuição da corrente de armadura, reduzindo o torque elétrico e, consequentemente, a velocidade do motor.
Entretanto, a queda de velocidade do motor CC é mais acentuada do que a queda de velocidade do motor shunt.
O controle da velocidade do motor série é feito mediante o ajuste da tensão terminal ou inserindo-se uma resistência em série com o circuito de armadura.
Motor CC composto
São motores que possuem os campos shunt e série. Da mesma forma do que os geradores, são classificados em:
Compostos aditivos
são aqueles em que a força magnetomotriz do campo shunt soma-se à força magnetomotriz do campo série. Os motores aditivos são divididos em:
• Longos
• Curtos
Compostos subtrativos
são aqueles em que a força magnetomotriz do campo shunt subtrai-se à força magnetomotriz do campo série. Os motores subtrativos são divididos em:
• Longos
• Curtos
Para se determinar se o efeito dos campos será aditivo ou subtrativo, usamos a mesma convenção dos transformadores. Correntes entrando no ponto das bobinas produzem um efeito aditivo das forças magnetomotrizes dos campos shunt e série:

Enquanto que, se temos em uma bobina a corrente entrando no ponto, e na outra a corrente saindo do ponto, essas correntes produzem um efeito subtrativo das forças magnetomotrizes dos campos shunt e série:

Para esse motor, temos as seguintes equações:
- $$V_t={E_a+(R_a+R_s)I}_a$$
- $$I_a=I_L-I_f$$
- $$V_f={(R_{aj}+R_f)I}_f$$
Por unir os campos série e shunt, o torque do motor composto é maior do que o torque do motor shunt e menor do que o motor série. Quando opera com cargas baixas, a influência do campo série é menor do que a do campo shunt.
Mão na Massa
Considere a curva de magnetização da Figura 39 para a resolução dos exercícios deste módulo.

Teoria na prática
Um motor shunt possui tensão terminal igual a 200 V. A velocidade nominal do motor é 1600 rpm e seu rendimento é 90%. Sabendo que a potência mecânica de saída é 15 HP, determine a corrente de linha desse motor.
A potência de entrada será:
$$P_{ent}=\frac{P_{saida}}{\eta}=\frac{15\times746}{0,9}=12,43 kW\ $$
A corrente de armadura será:
$$I_a=\frac{P_{ent}}{V_t}=\frac{12430}{200}=62\ A$$
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Ao longo destes três módulos conhecemos os conceitos fundamentais do estudo de máquinas elétricas de corrente contínua.
Inicialmente, vimos as características construtivas e a forma de obtenção da tensão induzida nos terminais da máquina. No segundo módulo, vimos os geradores CC, e no terceiro, os motores CC.
Acreditamos que, ao final desse estudo, você tenha a capacidade de conhecer a estrutura, o princípio de funcionamento e as características terminais das máquinas CC.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Descreveu as características construtivas dos geradores e motores de corrente contínua.
Examinou o funcionamento dos geradores de corrente contínua
Analisou o funcionamento dos motores de corrente contínua
