Descrição

Aplicação das equações matemáticas no estudo do equilíbrio estático de um corpo rígido em termos translacionais e rotacionais.

PROPÓSITO

Compreender os conceitos e as equações do equilíbrio estático do corpo rígido para o aprendizado do dimensionamento de estruturas.

Preparação

Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e uma calculadora científica ou use a calculadora de seu smartphone/computador.

OBJETIVOS

Módulo 1

Identificar os principais vínculos de uma estrutura bidimensional

Módulo 2

Reconhecer os sistemas de forças e as condições de equilíbrio de um corpo rígido

Módulo 3

Esquematizar o diagrama do corpo livre (DCL)

Módulo 4

Reconhecer as reações nos vínculos de uma estrutura bidimensional

MÓDULO 1

Identificar os principais vínculos de uma estrutura bidimensional

Introdução

Boas-vindas ao estudo do equilíbrio dos corpos rígidos.

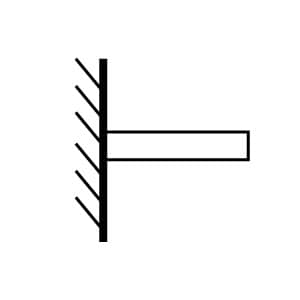
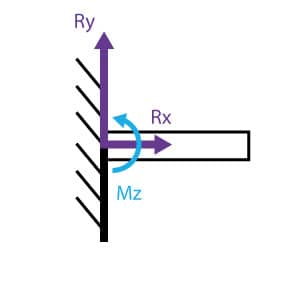
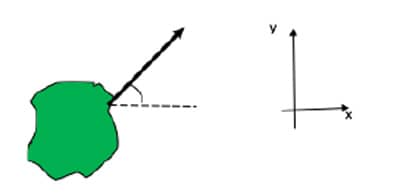
No estudo do equilíbrio dos corpos rígidos, a primeira fase consiste em reconhecer os vínculos da estrutura. As estruturas bidimensionais ou tridimensionais em equilíbrio estático sempre estão presas a apoios que restringem um ou mais tipos de movimentos (translação ou rotação): são os vínculos. Por exemplo, um vínculo pode restringir os movimentos de translação nas direções x e y e permitir a rotação em torno do eixo z (grau de liberdade). Observe nas figuras 1 e 2 um vínculo (apoio) do tipo engaste em que três restrições são impostas à estrutura: as translações vertical e horizontal e a rotação.

Vínculos em estruturas bidimensionais

Estudo qualitativo dos vínculos

Toda estrutura em equilíbrio estático apresenta-se “presa” a apoios ou vínculos. Dessa forma, restrições são impostas ao seu movimento. Imagine uma mesa no jardim de uma pequena cidade. Ela encontra-se em equilíbrio estático e impedida de realizar qualquer movimento de translação ou de rotação em virtude de estar “presa” por intermédio de vínculos. Inicialmente, a abordagem do tema será para estruturas bidimensionais, por exemplo, localizadas no plano xy do papel, com carregamento também nesse plano.

Quando se é realizado o estudo do equilíbrio estático de uma estrutura bidimensional, surgem três classes de apoios cujas denominações remetem-se diretamente ao número de restrições que elas impõem ao movimento, seja o de translação ou o de rotação. No plano, três são as possibilidades de restrição:

Uma translação
Duas translações
Duas translações e uma rotação

Sendo assim, naturalmente surgem os nomes para os apoios (vínculos): 1º, 2º ou 3º gêneros.

Clique nas barras para ver as informações. Objeto com interação.

Apoio (vínculo) de primeiro gênero

Quando a estrutura se encontra presa a um apoio de primeiro gênero, ela é impedida (restrição) de transladar em única direção (eixo). A esse vínculo, associa-se uma força de reação na direção desse eixo.

Apoio (vínculo) de segundo gênero

Quando o apoio que suporta a estrutura é do segundo gênero, duas restrições perpendiculares são impostas, impedindo translações nos dois eixos. Da mesma maneira que no vínculo de primeiro gênero, são utilizadas forças para representar as restrições impostas. Nesse caso, também é possível supor o mesmo número de incógnitas (duas): a direção e o módulo da força de reação sobre o vínculo.

Apoio (vínculo) de terceiro gênero

No apoio denominado de terceiro gênero, também popularmente conhecido como “engaste” ou “engastamento”, são impostas duas restrições à translação e uma à rotação. Fisicamente, essas restrições são representadas por forças (translação) e momento (rotação). As três incógnitas que surgem no engaste podem ser observadas sobre outro prisma, um momento e uma força (direção e módulo desconhecidos).

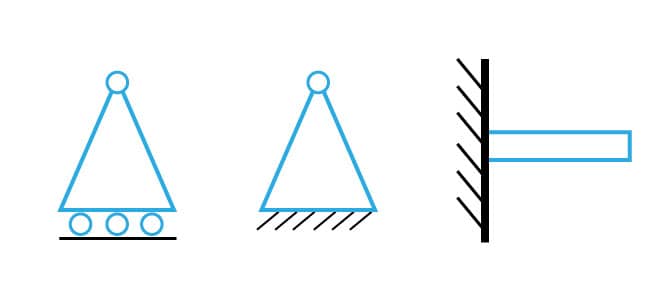
A figura 3 ilustra a representação mais comum para os três apoios citados. Observe que existem rótulas na parte superior dos apoios de primeiro e segundo gênero, não restringindo movimentos de rotação. Observe, ainda, na figura 3, as representações desses vínculos.

Reações nos vínculos de estruturas bidimensionais

Na análise dos problemas de estática, um dos primeiros passos é o desenho do diagrama do corpo livre (DCL), a ser estudado com detalhes ainda neste módulo. Nesse desenho, todos os carregamentos ou forças devem ser representados. O acréscimo ou a falta de algum comprometerá o estudo do equilíbrio do corpo rígido. Seguindo essa linha de raciocínio, no desenho do DCL, todos os apoios que estão na estrutura devem ser substituídos por forças ou momentos, dependendo do tipo de restrição que cada um impõe (translação ou rotação). Faremos uma análise simples dessa troca de forças/momentos.

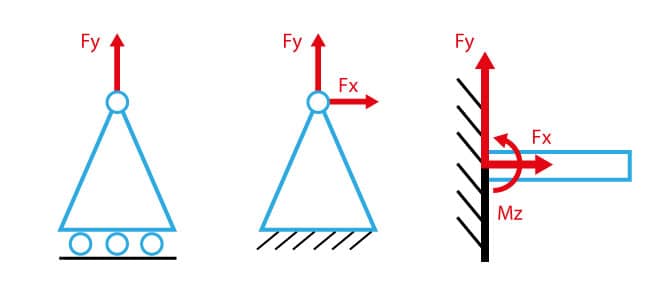
Na figura 4, os três principais apoios estudados anteriormente estão dispostos com as respectivas substituições por força ou momento, concernentes às restrições impostas. Como os apoios de primeiro e segundo gêneros restringem translação, os entes físicos utilizados nessa substituição são forças e, no caso do apoio de terceiro gênero, ocorrem restrições a translações e à rotação. Nesse vínculo, os entes físicos utilizados na substituição são forças e momento. É comum denominar as forças e os momentos associados aos vínculos de reações nos apoios.

Saiba mais

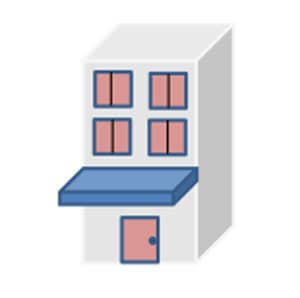
Os apoios de terceiro gênero também são conhecidos por permitirem que a estrutura se mantenha “em balanço”, ou seja, uma das extremidades livre e a outra engastada numa parede, por exemplo. Possivelmente, o exemplo mais presente em nosso dia a dia seja a marquise, em que uma pequena laje apresenta uma extremidade presa (engastada) à estrutura de um prédio e a outra extremidade livre, remetendo diretamente à ideia que a denomina “em balanço”.

A figura 5 apresenta uma representação esquemática de uma marquise. Note que uma de suas extremidades apresenta-se presa à estrutura, com restrições à translação e à rotação, enquanto a outra extremidade encontra-se livre. A ideia do balanço fica bem explícita nesse elemento.

Graus de liberdade

Em sua obra, Curso de Mecânica, o autor Adhemar Fonseca apresenta o conceito de grau de liberdade que será, de forma sucinta, abordado neste tópico.

Exemplo

Supondo um sistema com resultante das forças igual a $\vec{R}$ , ela tende a provocar a translação ao longo de um eixo e, similarmente, uma rotação em torno de um eixo, o vetor momento resultante $\vec{M}$ . Tratando os vetores $\vec{R}$ e $\vec{M}$ no espaço xyz, é possível a decomposição de cada um deles em até três componentes. Assim, no espaço, a estrutura tem até 6 graus de liberdade (não restrição), sendo 3 translações e 3 rotações. Para estruturas no plano, a resultante terá duas componentes e o momento apenas uma, num eixo perpendicular ao plano das forças. Em consequência, são 3 os graus de liberdade possíveis.

A função do vínculo é restringir alguns graus de liberdade. Portanto, os vínculos em estruturas (em equilíbrio estático) podem ser classificados em função do número de graus de liberdade existentes.

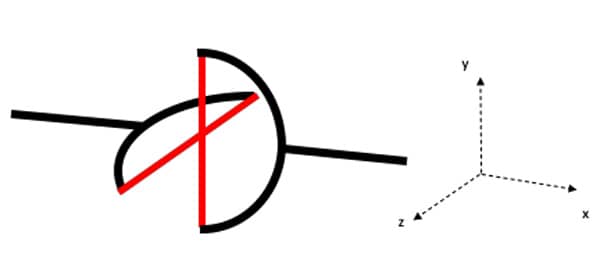
No caso espacial, de 0 a 5 graus de liberdade e, na situação do plano, de 0 a 2 graus de liberdade. Como exemplo, é possível citar o vínculo denominado junta universal apresentado na figura 6. Observe que é um vínculo com dois graus de liberdade (rotações em torno de y e z) ou ainda, quatro restrições (três translações em x, y e z e uma rotação em torno de x).

Teoria na prática

Na Engenharia, a presença de estruturas equilibradas e com diversos tipos de apoios está muito presente no dia a dia. Como foi visto neste módulo, três classes são possíveis para os vínculos. Para que você possa perceber isso na prática, alguns exemplos de situações reais serão apresentados neste tópico.

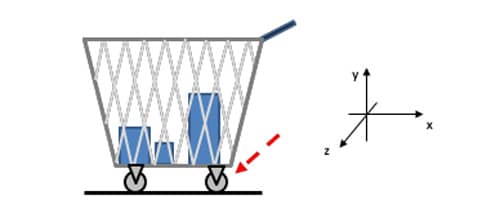
Inicialmente, imagine um carrinho de compras. As rodinhas traseiras (com seu sistema de fixação ao carrinho) comportam-se como um apoio de primeiro gênero. Uma restrição é imposta, a da translação no eixo y, ou seja, ∆y = 0. Contudo, não há impedimento de outros dois movimentos: translação no eixo x (∆x ≠ 0) e rotação em torno do eixo z (∆θ_z ≠ 0). Observe a figura a seguir de um esboço de um carrinho de compras.

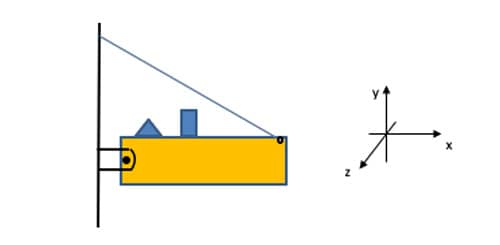
Outra possibilidade de vínculo estudado e com aplicação na prática é o apoio de segundo gênero, cujas translações nos eixos x e y são impedidas (∆x = 0 e ∆y = 0), mas não a rotação em torno do eixo z (∆θ_z ≠ 0). Veja na figura seguinte o exemplo de uma estrutura composta por uma viga presa em uma das extremidades pelo apoio de segundo gênero e na outra extremidade por um cabo de aço. A extremidade unida ao vínculo apresenta restrição aos movimentos vertical e horizontal da viga, mas a rotação é possível. Observe o esquema da figura.

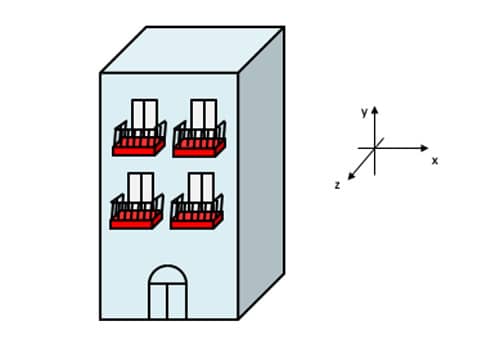
Neste módulo, foi visto o apoio de terceiro gênero, o que impõe as três restrições, as duas translações nos eixos x e y (∆x = 0 e ∆y = 0) e, também, a rotação em torno do eixo z (∆θ_z = 0). Exemplos clássicos são as varandas e as marquises. Na figura seguinte, uma estrutura em balanço é apresentada na forma de uma pequena varanda.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Vínculos em estruturas bidimensionais - exemplos reais.

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 2

Reconhecer os sistemas de forças e as condições de equilíbrio de um corpo rígido

Introdução

No estudo do equilíbrio de um corpo rígido, os dois entes físicos que caracterizam esse estado são a resultante das forças $\vec{R}$ e a soma dos momentos $\vec{M}$ aplicados por elas. Quando $\vec{R}$ e $\vec{M}$ são simultaneamente nulos, está garantido o equilíbrio, que é dividido em estático e dinâmico. No primeiro, além das condições para $\vec{R}$ e $\vec{M}$ , sua velocidade é zero. No equilíbrio dinâmico, a diferença é que o sistema apresenta movimento retilíneo uniforme (MRU), ou seja, velocidade constante.

Conceitos de força e de momento de uma força

No módulo 1, foram citados dois conceitos: o de força e o de momento de uma força. No dia a dia, esses dois entes físicos apresentam-se com bastante frequência, mas é fundamental para o futuro engenheiro conhecê-los com profundidade. Inicialmente, a abordagem será qualitativa. Veja as duas situações a seguir:

Clique nas informações a seguir. Clique nas informações a seguir.

Situação 1

Suponha a situação em que uma pessoa movimente a cadeira para sentar-se à mesa. Mesmo não conhecendo o conceito oficial de força, é bastante intuitiva a ideia de que foi necessário atuar na cadeira para que ela se movimentasse. Relacionado a essa situação, surge o juízo popular do ente físico força.

Situação 2

Se a situação imaginada for a de trocar o pneu furado de um carro, será preciso atuar de tal forma na retirada dos parafusos que ocorra uma rotação deles. Surge a ideia do momento provocado por uma força, associando-o à rotação provocada por esta.

É claro que os conceitos de força e de momento se conservam mesmo em situações complexas da Engenharia. A ponte que liga o Rio de Janeiro a Niterói apresenta uma série de exemplos em que forças atuam em sua estrutura e que provocam momentos. Uma diferença bastante perceptível é a quantidade desses elementos nessas estruturas complexas.

Conceito matemático de força

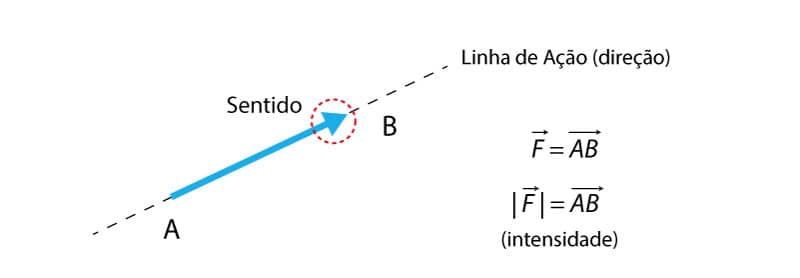
A força é uma grandeza vetorial (representada por um vetor) e, por isso, apresenta as seguintes características: módulo (ou intensidade), direção (linha de ação da força) e sentido.

Associada a esses atributos, segue-se uma unidade que pode ser kgf (quilograma-força), N (newton), dyn (dina) etc. A figura 6 mostra a representação de uma força $\vec{F}$ e seus atributos.

Você sabia

No Sistema Internacional de Unidades (S.I.), a força é apresentada em newtons (N), em homenagem aos brilhantes trabalhos do físico Isaac Newton (1642-1727) na Mecânica Clássica.

Forças (cargas) concentrada e distribuída

Na Engenharia, é importante salientar a diferença entre os conceitos de força concentrada e força distribuída.

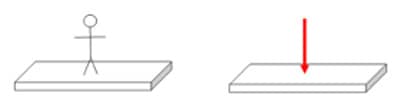
No caso da força concentrada, existe um único ponto de aplicação sobre a estrutura. Para exemplificar, suponha uma pessoa de pé em um apartamento. A força que ela faz sobre a laje é considerada uma força concentrada. Observe a figura 7 que, de maneira esquemática, apresenta a situação descrita.

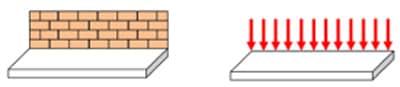
A força ou carga distribuída apresenta atuação ao longo de um comprimento. Um exemplo clássico na Engenharia de força distribuída é a parede de um apartamento. Observe o esquema apresentado na figura 8 em que a representação gráfica de uma carga distribuída é mostrada.

Atenção

É importante ressaltar que, no S.I., a força concentrada é apresentada em N e a força (carga) distribuída, em N/m.

Força escrita em função de suas componentes retangulares

A força é uma grandeza vetorial e, por isso, pode ser representada por suas componentes retangulares x, y e z.

Para uma compreensão gradual do tema, abordaremos uma força localizada no plano xy e, depois, a situação em que a força se encontra no espaço xyz.

Força no plano escrita em função de suas componentes retangulares

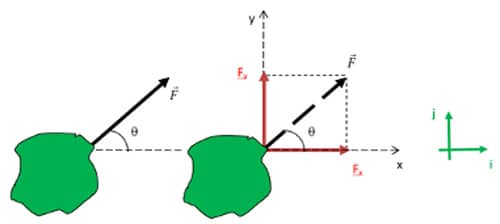
Suponha o plano xy do papel e considere um sistema submetido a uma força oblíqua $\vec{F}$ , conforme a representação da figura 9.

Tomando-se como referência o par de eixos cartesianos x e y, qualquer vetor no plano pode ser escrito a partir de suas componentes retangulares F_x e F_y, que representam seus módulos nas direções x e y, respectivamente. Além disso, são utilizados os vetores unitários i (1,0) e j (0,1). No caso do vetor que representa a força $\vec{F}$ , pode-se escrevê-lo conforme a equação 1:

$\vec{F} = F_{x} . i + F_{y} . j$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 1

A figura 10 mostra a representação geométrica da decomposição da força $\vec{F}$ em suas componentes retangulares F_x e F_y.

A partir das relações trigonométricas no triângulo retângulo, é possível escrever as equações matemáticas 2 e 3 para as componentes retangulares da força $\vec{F}$ e sua direção θ :

$F_{x} = F . \cos θ e F_{y} = F . s e n θ$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 2

$t g θ = \frac{F_{y}}{F_{x}} \to θ = a r c t g (\frac{F_{y}}{F_{x}})$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 3

A partir das equações 1 e 2 e utilizando os vetores unitários i e j, é possível reescrever a força $\vec{F}$ conforme a equação 4.

$\vec{F} = F . \cos θ . i + F . s e n θ . j$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 4

Ainda utilizando as ferramentas matemáticas da geometria plana, é possível perceber, na figura 10, um triângulo retângulo cujos catetos são as componentes F_x e F_y e a hipotenusa F. A partir da relação matemática conhecida como teorema de Pitágoras, é verdade a relação entre os módulos de F_x, F_y e F, mostrados na equação 5.

${F_{x}}^{2} + {F_{y}}^{2} = F^{2}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 5

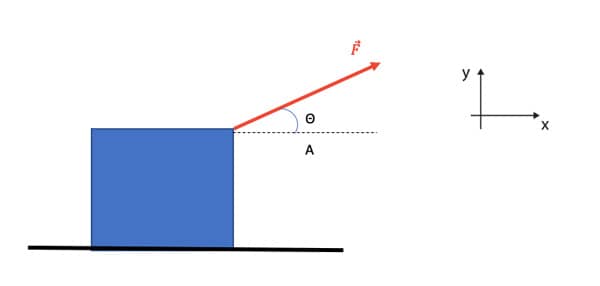
Atividade

Seja a força apresentada na figura e o par de eixos xy. O módulo da força é 100N e o ângulo θ que o vetor força forma com o eixo x é tal que o seno vale 0,6 e o cosseno, 0,8. Escreva a força F em coordenadas retangulares.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

A partir da equação 2, é possível determinar as projeções da força F sobre os eixos x e y, ou seja:

$F_{x} = F . \cos θ e F_{y} = F . s e n θ$

$F_{x} = 100 . 0, 8 = 80 N e F_{y} = 100 . 0, 6 = 60 N$

Utilizando a equação 4, a força F pode ser escrita na forma retangular.

$\vec{F} = F . c o s θ . i + F . s e n θ . j$

$\vec{F} = 80 . i + 60 . j$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Força no espaço escrita em função de suas componentes retangulares

Generalizando uma força $\vec{F}$ como um vetor no R³, além dos eixos x e y, deve-se utilizar o eixo z para a decomposição da força em coordenadas retangulares. Além disso, os vetores unitários serão $i$ (1, 0, 0), $j$ (0, 1, 0) e $k$ (0, 0, 1) que representam, respectivamente, os sentidos dos eixos x, y e z.

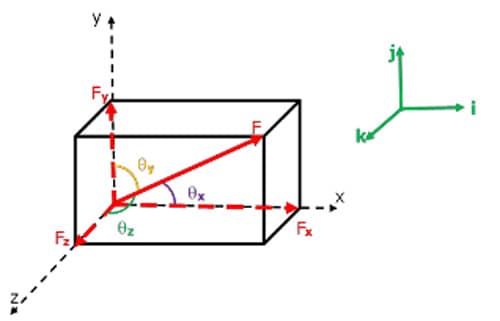
A figura 11 representa esquematicamente a força $\vec{F}$ no espaço e os eixos x, y e z. Além disso, são mostrados os ângulos θ_x,θ_y e θ_z que a força $\vec{F}$ forma com os eixos. Ainda é possível perceber as projeções da força nos eixos x, y e z, ou seja, F_x, F_y e F_z.

A partir da figura 11, observando triângulos retângulos e utilizando a definição da função trigonométrica cosseno, é possível escrever as relações matemáticas descritas nas equações 6, 7 e 8.

$\cos θ_{x} = \frac{F_{x}}{F} \to F_{x} = F . \cos θ_{x}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 6

$\cos θ_{y} = \frac{F_{y}}{F} \to F_{y} = F . \cos θ_{y}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 7

$\cos θ_{z} = \frac{F_{z}}{F} \to F_{z} = F . \cos θ_{z}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 8

Onde $\cos θ_{x}$ , $\cos θ_{y}$ e $\cos θ_{z}$ são denominados cossenos diretores.

Atenção

É possível mostrar que $\cos^{2} θ_{x}$ + $\cos^{2} θ_{y}$ + $\cos^{2} θ_{z}$ = 1.

A partir das equações anteriores, é possível reescrever a força $\vec{F}$ , em termos de suas coordenadas retangulares, e os vetores unitários $i$ , $j$ e $k$ , conforme a equação 9:

$\vec{F} = F . \cos θ_{x} . i + F . \cos θ_{y} . j + F . \cos θ_{z} . k$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 9

Atividade

Suponha que uma força de intensidade $10 k N$ atue de tal forma em uma estrutura que seus cossenos diretores valham $\frac{\sqrt{2}}{2}, \frac{3 . \sqrt{2}}{10} e \frac{2 \sqrt{2}}{5}$ . O engenheiro precisa escrever essa força em coordenadas retangulares e solicita que seu estagiário resolva.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Inicialmente, o estagiário transformou a unidade e encontrou para o módulo da força o valor de $10.000 N$ . A partir das equações 6, 7 e 8, ele determinou as componentes da força F nas direções dos eixos x, y e z.

$F_{x} = F . \cos θ_{x} \to F_{x} = 10000 . \frac{\sqrt{2}}{2} = 7071 N$

$F_{y} = F . \cos θ_{y} \to F_{y} = 10000 . \frac{3 . \sqrt{2}}{10} = 4243 N$

$F_{z} = F . \cos θ_{z} \to F_{z} = 10000 . \frac{2 \sqrt{2}}{5} = 5657 N$

Utilizando a equação 9, conseguiu determinar a força F em coordenadas retangulares, ou seja:

$\vec{F} = F . \cos θ_{x} . i + F . \cos θ_{y} . j + F . \cos θ_{z} . k$

$\vec{F} = 7071 . i + 4243 . j + 5657 . k$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Resultante de forças

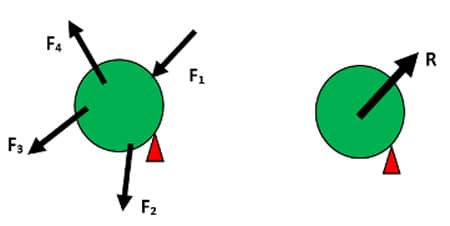
Seja uma estrutura em que atue um conjunto com “n” forças. Por razões simplificadoras matemáticas, é possível fazer a substituição desse conjunto de forças por uma única, denominada resultante das forças ou, simplesmente, resultante. Essa substituição matemática não altera a consequência física. A figura 12 apresenta uma estrutura em que agem quatro forças coplanares e a substituição delas pela força resultante.

A resultante das forças que agem sobre um corpo é a soma vetorial dessas forças. É possível fazer a decomposição retangular das várias forças e agrupar “os termos semelhantes” (em i, em j e em k). A equação 10 mostra essa descrição.

$\vec{R} = \sum_{} \vec{F_{i}} \to \vec{R} = (\sum_{} F_{x}) . i + (\sum_{} F_{y}) . j + (\sum_{} F_{z}) . k$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 10

Atenção

Para duas forças de módulos F₁ e F₂, é verdade que o módulo da resultante R entre elas está no seguinte intervalo:

$|\begin{matrix} F_{1} - & F_{2} \end{matrix}| \leq R \leq |\begin{matrix} F_{1} + & F_{2} \end{matrix}|$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Atividade

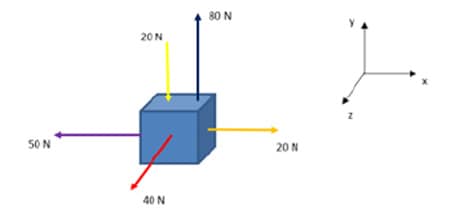
Suponha que um corpo esteja sob a ação de várias forças nas direções dos eixos ortogonais x, y e z, conforme a figura. Determine a resultante das forças.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Inicialmente, deve-se observar os eixos desenhados e suas respectivas orientações positivas (setas). Após identificar as resultantes em cada eixo, é possível aplicar a equação 10 para determinar a resultante no corpo.

$\vec{R} = \sum_{} \vec{F_{i}} \to \vec{R} = (\sum_{} F_{x}) . i + (\sum_{} F_{y}) . j + (\sum_{} F_{z}) . k$

$\sum_{} F_{x} = 20 - 50 = - 30 N$

$\sum_{} F_{y} = 80 - 20 = 60 N$

$\sum_{} F_{z} = 40 N$

Substituindo na equação 10, tem-se:

$\vec{R} = - 30 . i + 60 . j + 40 . k$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Momento de uma força em relação a um ponto

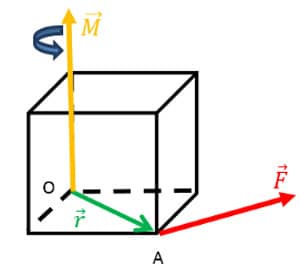
Considere um sistema e uma força $\vec{F}$ atuando sobre ele no ponto A, conforme a figura 13. Suponha que no ponto O exista um vínculo de segundo gênero. O vetor que liga os pontos O e A é denominado vetor posição $\vec{r} = \vec{O A}$ (ver figura 13). Nas condições anteriormente apresentadas, é intuitivo imaginar que a força $\vec{F}$ fará o corpo girar. Essa rotação do corpo é o momento provocado pela força em relação ao ponto O.

Observando a figura 13, é possível perceber que o vetor momento $\vec{M}$ é perpendicular ao plano formado pela força $\vec{F}$ e o vetor posição $\vec{r}$ . Além disso, é possível observar que ele apresenta um sentido de rotação.

O momento de uma força em relação a um ponto é dado por um produto vetorial, conforme mostra a equação 11.

$\vec{M} = \vec{r} \times \vec{F}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 11

Escrevendo os vetores posição $\vec{r}$ (r_x, r_y e r_z) e a força $\vec{F}$ (F_x, F_y e F_z) em coordenadas retangulares, obtém-se o vetor momento $\vec{M}$ a partir do determinante a seguir.

$\vec{M} = |\begin{matrix} i & j & k \\ r_{x} & r_{y} & r_{z} \\ F_{x} & F_{y} & F_{z} \end{matrix}|$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Atenção

O vetor momento estará escrito em função das coordenadas retangulares.

Clique na barra para ver as informações. Objeto com interação.

O que acontece quando a força e o vetor posição são coplanares?

O módulo do momento aplicado por essa força, em relação a um ponto, pode ser determinado pelo produto da força pela distância do ponto à linha de ação da força (M = F . d). Observe o esquema a seguir.

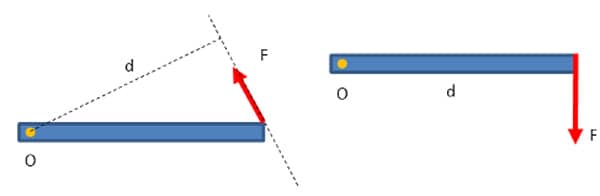
Na primeira figura, a força faz a barra girar em torno do ponto O no sentido anti-horário, então o momento é positivo. Na segunda, o sentido é horário, logo, o momento é negativo.

Atividade

Suponha que uma força F (10, 20, 30), em N, seja aplicada num ponto A de coordenadas (1, 2, 5). Determine o momento dessa força em relação à origem O (0, 0, 0) dos eixos x, y e z.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

O vetor posição

\vec{r} = \vec{O A} = A - O = (1, 2, 5) - (0, 0, 0) = (1, 2, 5)

A força F já se encontra escrita com suas coordenadas. Assim, aplicando-se o produto vetorial $\vec{M} = \vec{r} \times \vec{F}$ , da equação 11, é possível determinar o vetor momento.

$\vec{M} = |\begin{matrix} i & j & k \\ 1 & 2 & 5 \\ 10 & 20 & 30 \end{matrix}| = 60 i + 20 k + 50 j - 20 k - 30 j - 100 i = - 40 i + 20 j + 0 k$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equilíbrio estático de um corpo rígido

Suponha um corpo rígido tridimensional com carregamento genérico (várias forças concentradas/distribuídas e momentos). Para garantir o equilíbrio estático de um corpo rígido, os movimentos de translação e rotação não devem existir. Assim, estarão restritas as translações e as rotações concernentes aos três eixos cartesianos x, y e z. A fim de garantir que a translação e a rotação de um sistema sejam nulas, a resultante das forças e a resultante dos momentos devem ser iguais a zero. A equação 12 traduz o descrito de maneira matemática.

$\vec{R} = \sum_{} \vec{F_{i}} = \vec{0}$ e $\vec{M} = \sum_{} {\vec{M}}_{i} = \vec{0}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Equação 12

Como foi visto nos itens anteriores, é possível escrever a resultante das forças, assim como o momento resultante, em função de suas componentes retangulares. Para garantir o equilíbrio estático do sistema, basta que cada uma das componentes retangulares seja igual a zero. Surgem, dessa maneira, seis equações para o equilíbrio:

$\sum_{} F_{x} = 0$

$\sum_{} F_{y} = 0$

$\sum_{} F_{z} = 0$

$\sum_{} M_{x} = 0$

$\sum_{} M_{y} = 0$

$\sum_{} M_{z} = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Portanto, as seis equações supracitadas são necessárias e suficientes para garantir o equilíbrio estático do corpo rígido.

Quais equações de equilíbrio estático utilizar em diferentes situações?

Clique nas informações a seguir. Clique nas informações a seguir.

Para garantir a não translação

Para garantir a não rotação

Quando o carregamento for no plano

$\sum_{} F_{x} = 0; \sum_{} F_{y} = 0 e \sum_{} F_{z} = 0$

$\sum_{} M_{x} = 0; \sum_{} M_{y} = 0 e \sum_{} M_{z} = 0$

$\sum_{} F_{x} = 0; \sum_{} F_{y} = 0 e \sum_{} M_{z} = 0$

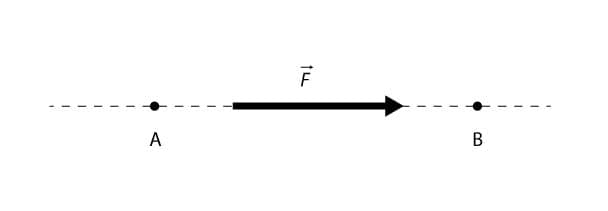
Obs.: Para escrever uma força a partir de dois pontos A (x_A, y_A, z_A) e B (x_B, y_B, z_B) de sua linha de ação, deve-se inicialmente escrever o vetor unitário e depois multiplicá-lo pelo módulo dessa força. Segue a sequência desses passos:

Clique nas barras para ver as informações. Objeto com interação.

Determinação do vetor unitário na direção

\vec{A B}

$λ_{\vec{A B}} = \frac{B - A}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})}{|\begin{matrix} \vec{A B} \end{matrix}|}$

onde,

$|\begin{matrix} \vec{A B} \end{matrix}| = \sqrt{{(x_{B} - x_{A})}^{2} {+ (y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Multiplicação do módulo de

\vec{F}

pelo vetor unitário. Assim,

\vec{F} = λ_{\vec{A B}} . F

Exemplo: Considere uma força $F$ de intensidade $100 N$ que passe pelos pontos A (1, 3, 5) e B (4, 3, 9), tal que seu sentido seja do vetor $\vec{A B}$ . Determine a força em coordenadas retangulares.

Solução: Determinação do vetor unitário na direção do vetor $\vec{A B}$

$λ_{\vec{A B}} = \frac{B - A}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})}{|\begin{matrix} \vec{A B} \end{matrix}|}$

$λ_{\vec{A B}} = \frac{(4, 3, 9) - (1, 3, 5)}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(3, 0, 4)}{|\begin{matrix} \vec{A B} \end{matrix}|}$

Mas,

$|\begin{matrix} \vec{A B} \end{matrix}| = \sqrt{{(x_{B} - x_{A})}^{2} {+ (y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}} = \sqrt{{(3)}^{2} {+ (0)}^{2} + {(4)}^{2}} = \sqrt{9 + 0 + 16} = \sqrt{25} = 5$

Assim,

$λ_{\vec{A B}} = \frac{(3, 0, 4)}{5}$

Para determinar o vetor F, basta utilizar a equação a seguir:

$\vec{F} = λ_{\vec{A B}} . F$

$\vec{F} = \frac{(3, 0, 4)}{5} . 100 = (3, 0, 4) . 20 = (60, 0, 80) N$

Teoria na prática

Na Engenharia, o equilíbrio das estruturas é muito presente. Não faltam exemplos práticos, como torres de transmissão, estruturas treliçadas (Linha Vermelha no Rio de Janeiro, por exemplo), dentre tantos outros. Em linhas gerais, o equilíbrio translacional e o rotacional devem ser garantidos nessas estruturas. Um exemplo simplificado, porém, que não deixa de auxiliar na aplicação das equações do equilíbrio em casos práticos, será realizado. A seguir, tem-se uma questão apresentada em um concurso.

(FCM-PB – 2015) O guindaste (também chamado de grua e, nos navios, pau de carga) é um equipamento utilizado para a elevação e a movimentação de cargas e materiais pesados, assim como a ponte rolante a partir do princípio da Física, segundo o qual uma ou mais máquinas simples criam vantagem mecânica para mover cargas além da capacidade humana. São comumente empregados nas indústrias, terminais portuários e aeroportuários, onde se exige grande mobilidade no manuseio de cargas e transporte de uma fonte primária (embarcação, trem ou elemento de transporte primário, ou mesmo avião) para uma fonte secundária (um veículo de transporte ou depósitos locais). Podem descarregar e carregar contêineres, organizar material pesado em grandes depósitos, efetuar a movimentação de cargas pesadas na construção civil, e as conhecidas pontes rolantes, ou guindastes móveis, são muito utilizadas nas indústrias de laminação e de motores pesados.

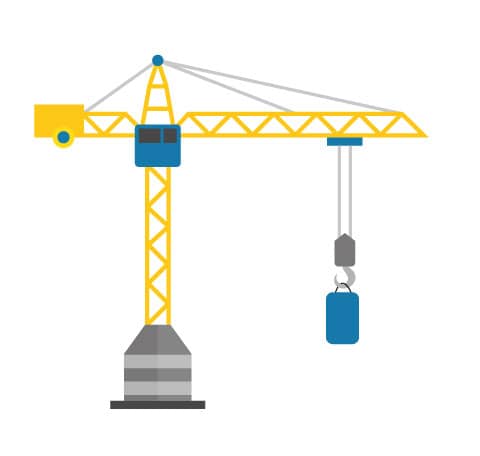
Um aluno, de posse de um simulador, projeta a grua acima com as seguintes características: o braço maior da grua tem comprimento de 16m, o braço menor, 4m; o contrapeso na extremidade do braço menor tem uma massa equivalente a 0,5 toneladas, e o centro de massa coincide com a extremidade do braço menor. A barra horizontal possui massa de 200kg, uniformemente distribuída, e a barra vertical está rigidamente fixada. De acordo com o projeto descrito, qual o peso máximo que essa grua poderá levantar sem tombar?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Equilíbrio rotacional de uma grua.

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 3

Esquematizar o diagrama do corpo livre (DCL)

Introdução

As estruturas bidimensionais ou tridimensionais em equilíbrio estático sempre estão presas a apoios (vínculos) que restringem um ou mais tipos de movimentos (translação ou rotação). Para realizar o estudo do equilíbrio do corpo rígido, há a necessidade de substituir os apoios pelas reações que eles provocam, além dos carregamentos externos. Esse desenho representa o diagrama do corpo livre (DCL).

Sistema de corpos rígidos

No estudo da Mecânica Clássica, um sistema pode ser composto por um ou mais corpos rígidos que estão unidos por meio de vínculos, transmissões, contato, campos etc. A análise matemática pode ser realizada considerando o conjunto ou parte dele. Neste módulo, não abordaremos a parte dinâmica da Mecânica, apenas a parte estática, ou seja, os equilíbrios translacional e rotacional.

Diagrama do corpo livre (DCL)

Na resolução dos problemas de Mecânica (estática), dois aspectos igualmente importantes devem ser utilizados:

Relações matemáticas do equilíbrio

É necessário ter domínio sobre os aspectos matemáticos para desenvolver o problema.

Desenho do diagrama do corpo livre

Neste caso, os aspectos físicos são fundamentais.

Qualquer dúvida a respeito do desenho do DCL implicará equações incorretas e, consequentemente, erros na solução de um problema. Sem hierarquizar a importância de um ou de outro aspecto, é fundamental compreender perfeitamente o DCL para, depois, escrever as equações do equilíbrio e, por fim, resolver o problema proposto.

Muitos autores denominam o diagrama do corpo livre como “isolar” o corpo do sistema. Independentemente da nomenclatura, é importante que, ao desenhar o diagrama (ou isolar o corpo), você consiga representar por meio de forças ou momentos os vínculos que são retirados nesse isolamento do corpo.

Nesse ponto, é ratificada a importância do estudo inicial dos vínculos e das reações associadas. Mais um aspecto relevante é a terceira lei de Newton, presente na separação dos corpos no sistema. Para que você relembre o conceito da terceira lei de Newton, o próximo tópico fará uma rápida abordagem do tema.

Terceira lei de Newton

A terceira lei de Newton, também conhecida como lei da ação e reação, afirma que, quando dois corpos interagem, eles “trocam” forças. Essas forças apresentam a mesma direção, o mesmo módulo (intensidade) e sentidos opostos. As forças de ação e de reação atuam em corpos distintos, portanto, não se anulam.

A figura 14 representa a descrição anterior.

As forças $\vec{f_{A B}}$ e $\vec{f_{B A}}$ constituem um par ação e reação e, portanto, apresentam mesma direção, mesma intensidade e sentidos opostos. A nomenclatura $\vec{f_{A B}}$ indica a força que o corpo A faz no corpo B.

Desenhando o DCL

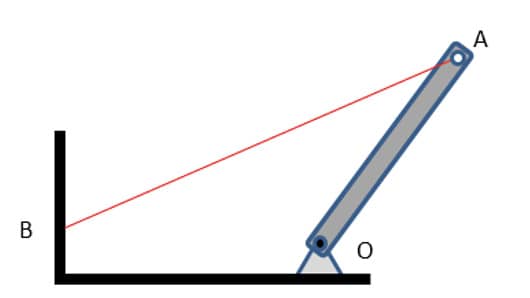
Para entender como desenhar o diagrama do corpo livre é fundamental perceber como os corpos ligados ao que será separado interagem com ele e de que maneira as forças reativas (dos vínculos) atuam sobre esse corpo. Essa é a “fase física” do problema. Esse estudo deve ser extremamente cuidadoso e talvez valha a pena “gastar” parte do tempo nessa análise para que eventuais erros não se propaguem na “fase matemática” da solução. A figura 15 apresenta um sistema simples, mas que ajudará no início do entendimento do desenho do DCL.

A figura 15 é um sistema composto por uma alavanca homogênea de peso $\vec{P}$ , um cabo de aço suposto ideal (inextensível e sem massa) e dois vínculos denominados B e O. O objetivo é isolar a alavanca do sistema, ou seja, enxergá-la isoladamente de forma abstrata. Em outras palavras, desenhar seu diagrama do corpo livre. Inicialmente, deve-se perceber que a barra está “interagindo” com o cabo de aço e com o apoio O, de segundo gênero. Além disso, existe a força exercida pelo campo gravitacional da Terra, o peso. Observe o diagrama do corpo livre dessa alavanca na figura 16.

Analisando o DCL da figura 16 é possível perceber a presença de três forças:

A força peso ( $\vec{P}$ ) exercida pelo campo gravitacional da Terra.
A força de tração ( $\vec{T}$ ) exercida pelo cabo de aço.
A forca $\vec{F}$ exercida pelo apoio de segundo gênero.

Atenção

Nesse momento do estudo, cabem duas observações importantes. A primeira é que a força $\vec{F}$ pode ser decomposta em duas componentes, sendo uma vertical e a outra horizontal (restrições de translações nesses eixos). A segunda é que, se um corpo está em equilíbrio sob a ação de 3 forças coplanares, ou essas forças são concorrentes (figura 16) ou são paralelas.

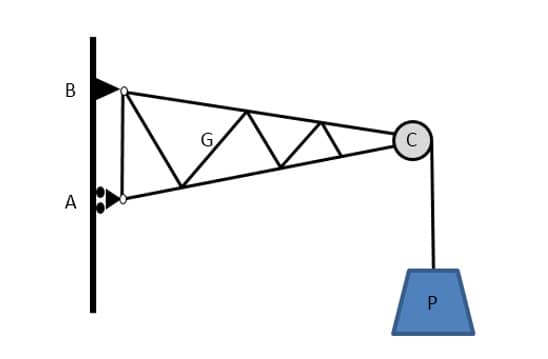
Observe a figura 17 em que um braço treliçado mantém em equilíbrio um corpo suspenso. Note que G é o centro de massa do braço, e A e B os vínculos de primeiro e segundo gêneros, respectivamente.

Analisando o DCL da figura 17, é possível perceber a presença de algumas forças:

A força peso do braço treliçado ( $\vec{P}$ _treliça) exercida pelo campo gravitacional da Terra.
A força de tração ( $\vec{T}$ ) exercida pelo cabo de aço.
O peso ( $\vec{P}$ ) e as reações nos apoios A e B.

Atenção

O braço treliçado está vinculado nos apoios A e B e sua extremidade C sustenta um corpo suspenso.

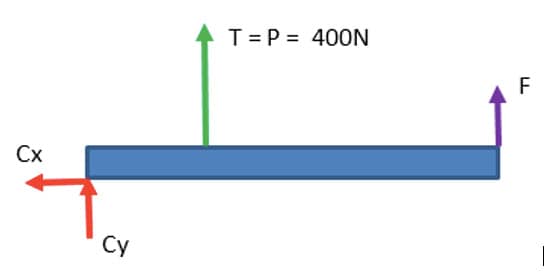
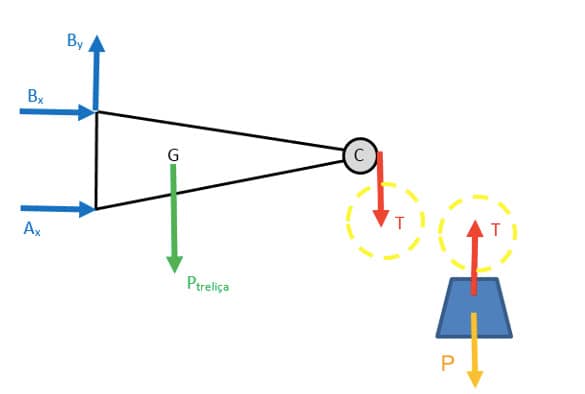
Para facilitar a análise do DCL do braço, será feito simultaneamente o DCL do corpo suspenso. Observe a figura 18, em que são desenhados os DCLs do braço treliçado e do corpo suspenso.

Analisando a figura 18, perceba que o corpo suspenso está sob a ação de duas forças indicadas:

Peso ( $\vec{P}$ )

Tração ( $\vec{T}$ )

E em relação aos DCLs?

As duas forças em destaque ( $\vec{T}$ ) constituem um par ação-reação.
O peso do braço treliçado $\vec{P}$ _treliça atua em seu centro de massa (G) e surgem as reações nos vínculos A e B.
A força de tração ( $\vec{T}$ ) atua na extremidade C do braço treliçado.
Uma vez que o vínculo B é do segundo gênero, ele impõe duas restrições, representadas pelas forças B_x e B_y.
O vínculo A, de primeiro gênero, só impõe uma restrição, por isso apenas a força A_x é indicada no DCL.

Quando você estiver dominando o desenho do diagrama do corpo livre, poderá avançar para a próxima etapa, as equações do equilíbrio e, assim, determinar as incógnitas que aparecem no DCL. No último exemplo, são elas: A_x, B_x e B_y.

Teoria na prática

Nos projetos de engenharia, várias são as fases até a concepção final de um produto. Neste tópico, veremos uma etapa importante em qualquer projeto de engenharia, do mais simples ao mais complexo: o diagrama do corpo livre. Qualquer imperfeição no DCL acarretará equações de equilíbrio erradas, o que levará a resultados diferentes dos reais.

Em qualquer situação na Engenharia, as estruturas estarão sob ação de efeitos diversos que se resumirão a dois entes físicos principais: forças e momentos. Para a determinação dessas forças e desses momentos, dois importantes aspectos deverão ser considerados: o desenho do diagrama do corpo livre (DCL) e as equações do equilíbrio bidimensional

$(\sum_{} F_{x} = 0, \sum_{} F_{y} = 0 e \sum_{} M_{z} = 0)$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

ou tridimensional

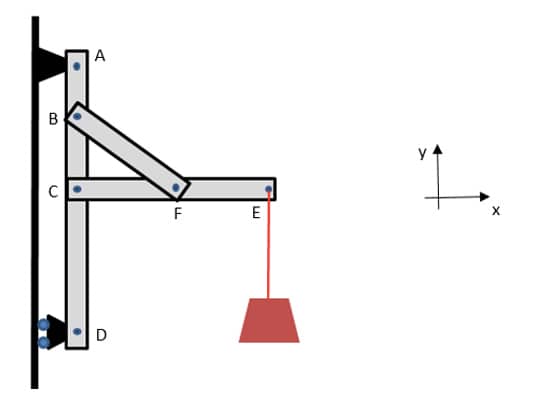
$(\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} F_{z} = 0, \sum_{} M_{x} = 0, \sum_{} M_{y} = 0 e \sum_{} M_{z} = 0)$ .

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para efeito de simplicidade no entendimento inicial do tópico, utilizaremos uma estrutura bidimensional para a análise de seu DLC. Considere o pórtico da figura a seguir que sustenta uma carga de peso P. Os pesos das barras que constituem o pórtico serão desprezados e os pontos A, B, C, D, e F apresentam pinos. Ratificando o que já foi estudado no módulo 1, perceba a presença de dois vínculos. Em A um apoio de segundo gênero e, em D, um apoio de primeiro gênero.

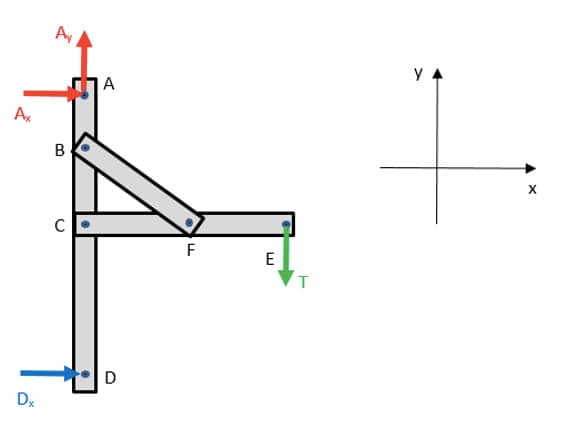
Na análise inicial do DCL será considerado o pórtico integralmente. As forças que agem são a tração no cabo ideal (em módulo, equivale ao peso do corpo suspenso) e as forças reativas nos apoios A e D.

No apoio de segundo gênero, as translações nos eixos x e y são impedidas (∆x= 0 e ∆y= 0), mas não a rotação em torno do eixo z (∆θ_z ≠ 0). Dessa forma, as forças A_x e A_y são marcadas no DCL. No apoio de primeiro gênero D, apenas a translação horizontal é impedida, sendo permitidas a translação em y e a rotação em z. Matematicamente, ∆x = 0, ∆y ≠ 0 e ∆θ_z ≠ 0. Em termos de reações, apenas a força horizontal D_x aparece no DCL.

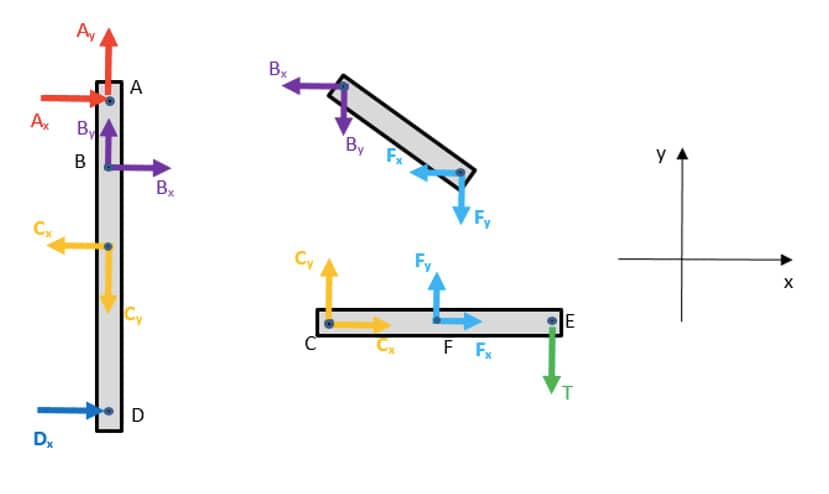
No segundo momento, as hastes que compõem o pórtico são separadas e seus DCLs são traçados. Os valores associados não são o objetivo desta análise, apenas as forças de maneira genérica (os sentidos são arbitrários nesse primeiro momento). Vale a pena ressaltar a presença da terceira lei de Newton (ação e reação). Observe o ponto B, que é a união de duas barras. Em um dos DCLs (na barra vertical), as forças que atuam são: uma vertical para cima e uma horizontal para a direita. De acordo com a terceira lei de Newton, na barra oblíqua, as forças terão sentidos opostos (mantendo constantes os módulos e as direções). Essa mesma análise pode ser observada em vários outros pontos de união das barras. Observe a figura a seguir.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Diagrama do corpo livre em um pórtico e aplicação da terceira lei de Newton.

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 4

Reconhecer as reações nos vínculos de uma estrutura bidimensional

Introdução

Nos módulos anteriores, os vínculos (apoios) foram apresentados gradativamente para que alguns conceitos começassem a ser entendidos. Neste módulo, aprofundaremos esse estudo. Lembre-se sempre de que desenhar o diagrama do corpo livre é uma etapa primordial na resolução de problemas e, para tanto, é necessário o perfeito conhecimento dos vínculos e das suas reações.

Vínculos

Quando se imagina uma estrutura em equilíbrio estático, deve-se fazer uma associação a vínculos que a mantêm “presa”. De forma mais técnica, apoios restringem movimentos de um corpo rígido ou de um sistema de corpos rígidos. São seis possibilidades, portanto. O impedimento de translações nas direções dos eixos cartesianos x, y e z e o impedimento de rotações em torno desses mesmos eixos. A situação ora exposta é a mais genérica possível e pode ocorrer para corpos com carregamentos tridimensionais. Uma abordagem mais simples, porém não menos importante e muito frequente na Engenharia, é o carregamento bidimensional. Dessa forma, faremos a releitura de alguns tópicos já apresentados, mas acrescentando novos conceitos.

Relembrando

No estudo do equilíbrio estático de uma estrutura com carregamento no plano que vimos no módulo 1, é possível classificar os apoios em três classes. Antes de continuar o estudo, é importante relembrar que, sendo o carregamento das forças no plano xy, os momentos gerados por elas serão vetores com a direção do eixo z (perpendicular ao plano xy). A explicação surge da definição de momento de uma força, que é o produto vetorial entre os vetores posição e força.

Resumindo

Em resumo, para o carregamento bidimensional, as forças reativas estarão no plano xy (podendo ser decompostas em suas projeções F_x e F_y) e os momentos estarão perpendiculares ao plano xy, podendo o vetor estar “entrando” ou “saindo” desse plano.

A partir dos aspectos descritos, faremos uma classificação dos apoios em estruturas bidimensionais e associação das reações (forças/momentos). A classificação é apenas uma ferramenta didática. O importante é que você reconheça o tipo de vínculo e saiba substituí-lo pelas restrições que ele promove à estrutura.

Os vínculos e suas reações

Com as premissas impostas no estudo de estruturas com carregamento bidimensional, é fácil concluir que três são os graus de liberdade dessa estrutura quando desconectada de um ou mais vínculos: translação no eixo x, translação no eixo y e rotação em torno do eixo z.

Clique nas barras para ver as informações. Objeto com interação.

Apoio de primeiro gênero

Neste vínculo, a ação da força é previamente conhecida. Contudo, o seu módulo é uma incógnita a ser descoberta. Em sua obra, os autores Beer e Johnston (1976) citam alguns exemplos desse tipo de apoio: roletes, balancins, superfícies lisas, cabos curtos, bielas, cursores e pinos deslizantes.

Obs.: Você pode encontrar os apoios citados nas obras indicadas no Explore +.

A figura 19 mostra alguns desses vínculos e a reação que determina a restrição, com sua linha de ação. Como regra, o sentido da força reativa é indefinido. Após o cálculo, valores positivos ratificam a escolha do sentido desenhado no DLC e valores negativos informam que o sentido arbitrado inicialmente é oposto ao real.

Observando a figura 19, perceba a transição entre a estrutura e o desenho do diagrama do corpo livre. Por exemplo, uma estrutura que possua um vínculo do tipo balancim, quando seu DCL for desenhado, deverá ser feita a troca por uma força única perpendicular à superfície. De maneira análoga, o procedimento é repetido para os demais vínculos. Fica explícita a importância de identificar o vínculo por sua representação geométrica e saber efetuar a troca pela reação correta no desenho do diagrama do corpo livre.

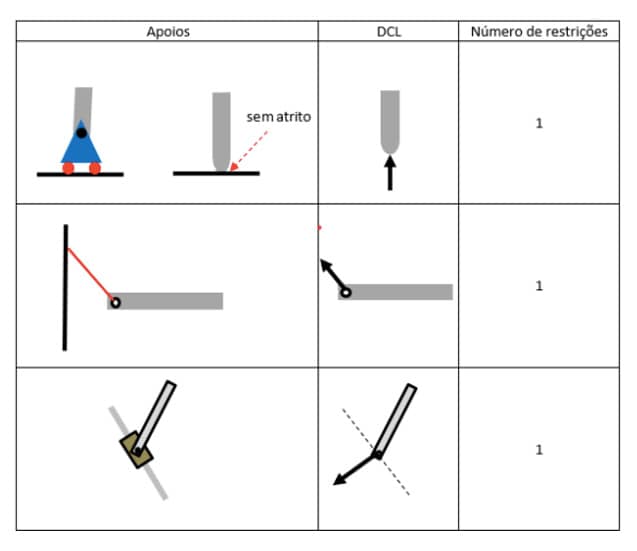
Figura 19 – Apoios de primeiro gênero. Fonte: Autor

Apoio de segundo gênero

Neste vínculo, tanto a linha de ação da força como o seu módulo são desconhecidos. São duas incógnitas a serem descobertas. Muitas vezes, faz-se a opção de substituir essa força com linha de ação desconhecida por suas projeções ortogonais. Em sua obra, os autores Beer e Johnston (1976) citam alguns exemplos desse apoio: os pinos regulares em orifícios ajustados, rótulas e superfícies rugosas.

Obs.: Você pode encontrar os apoios citados nas obras indicadas no Explore +.

A figura 20 mostra esses vínculos e as reações que impõem à restrição. Da mesma maneira que explicado no item (a), o sentido das forças reativas é indefinido. Após o cálculo, valores ratificam ou não a escolha do sentido desenhado no DLC. Valores positivos confirmam a escolha inicial e valores negativos informam que o sentido arbitrado inicialmente é oposto ao real.

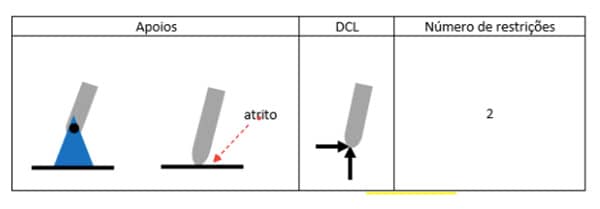
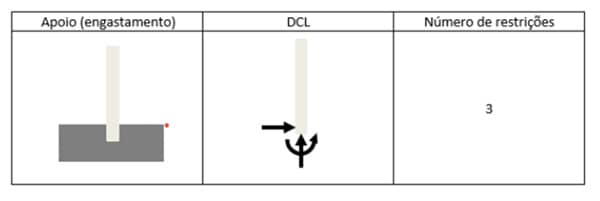
Figura 20 – Apoios de segundo gênero. Fonte: Autor

Apoio de terceiro gênero

Neste vínculo, as restrições impostas não são apenas de translação como nos dois primeiros tipos de vínculos. Soma-se uma restrição, a rotação. Sendo assim, a ação da força, seu módulo e o momento são desconhecidos. São três incógnitas a serem descobertas. É comum utilizar as duas projeções ortogonais da força reativa e o momento na troca do vínculo ao se desenhar o diagrama do corpo livre. Assim como explicado nos itens (a) e (b), os sentidos são inicialmente arbitrados e depois ratificados ou não pelos valores positivo ou negativo encontrados. O exemplo clássico desse apoio é o engaste, mostrado na figura 21. Observe o DCL e o número de restrições.

Figura 21 – Apoios de terceiro gênero. Fonte: Autor

Teoria na prática

As estruturas em equilíbrio estático na Engenharia apresentam-se vinculadas. Considerando um carregamento bidimensional, vimos as possibilidades de apoios. Um exemplo que reflete uma tendência atual na engenharia civil é o das pontes estaiadas, cuja beleza é incontestável. Vários são os exemplos pelo mundo. A de Millau, na França, as das cidades do Rio de Janeiro e de São Paulo etc.

Esquematicamente, a figura seguinte representa uma ponte estaiada e seus vários apoios, evidenciando algumas reações nos vínculos. É possível perceber os três gêneros de apoios. Além disso, os cabos apresentam papel estrutural na fixação dos tabuleiros das pontes estaiadas.

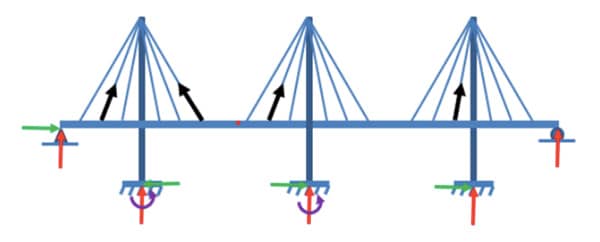
Esboço de uma ponte estaiada e as reações nos apoios. Fonte: Autor

Na figura, são colocadas de maneira genérica (os sentidos das forças e dos momentos são meramente ilustrativos) as reações que podem surgir nos diversos apoios, todas em função do grau de liberdade que cada apoio proporciona, ou ainda, das restrições impostas por eles. Genericamente, após o desenho do DCL, devem ser aplicadas as equações do equilíbrio, ou seja,

$\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} M_{z} = 0$ ,

Atenção! Para visualização completa da equação utilize a rolagem horizontal

para garantir que não existe translação nem rotação da estrutura.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Apresentação das reações dos vínculos em uma estrutura real – ponte estaiada.

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

Conclusão

Considerações Finais

Neste tema, foram abordados os principais aspectos do equilíbrio dos corpos rígidos. Inicialmente, identificamos os vínculos que mantêm a estrutura em equilíbrio. Apresentamos os tipos mais utilizados na Engenharia e suas atuações no equilíbrio da estrutura, seja restringindo a translação ou a rotação. Nessa fase do estudo, as restrições impostas pelos vínculos foram substituídas por entes físicos (forças/momentos) e, portanto, uma fase importante do objetivo do tema foi alcançada: o desenho do diagrama do corpo livre de um corpo rígido em equilíbrio. Em seguida foi observado, qualitativamente, que o equilíbrio de um corpo se refere, ao mesmo tempo, à não translação e à não rotação. Matematicamente, a resultante das forças e dos momentos devem ser nulos. Surgem, portanto, as equações do equilíbrio para um corpo bidimensional:

$\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} M_{z} = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Podcast

Agora, o professor Julio Cesar José Rodrigues Junior encerra o tema falando mais sobre o equilíbrio dos corpos rígidos.

CONQUISTAS

Você atingiu os seguintes objetivos:

Identificou os principais vínculos de uma estrutura bidimensional

Reconheceu os sistemas de forças e as condições de equilíbrio de um corpo rígido

Esquematizou o diagrama do corpo livre (DCL)

Reconheceu as reações nos vínculos de uma estrutura bidimensional

Referências

BEER, F. P.; JOHNSTON, E. R. J. Mecânica vetorial para engenheiros – Estática. 2. ed. v. 1. São Paulo: McGraw-Hill, 1976.

FONSECA, A. Curso de Mecânica – Estática. 3. ed. v.1. Rio de Janeiro: LTC, 1976.

HIBBELER, R. C. Resistência dos materiais. 7. ed. São Paulo: Pearson, 2010.

MERIAM, J. L.; KRAIGE, L. G. Mecânica para Engenharia – Estática. 7. ed. v.1. Rio de Janeiro: LTC, 2016.

Explore+

Para complementar o estudo de vínculos e grau de liberdade, leia as páginas de 150 a 166 da obra Curso de Mecânica – Estática (1976), de Adhemar Fonseca.
Para complementar o estudo de vínculos e reações, leia as páginas de 98 a 117 da obra Mecânica vetorial para engenheiros – Estática (1976), de Fernand P. Beer e Russel Johnston Jr.
Para complementar o estudo do equilíbrio do corpo rígido, leia o capítulo 3 da obra Mecânica para Engenharia – Estática (2016), de J. L. Meriam e L. G. Kraige

Conteudista

Julio Cesar José Rodrigues Junior

Currículo Lattes

Descrição

PROPÓSITO

Preparação

OBJETIVOS

Módulo 1

Módulo 2

Módulo 3

Módulo 4

MÓDULO 1

Introdução

Vínculos em estruturas bidimensionais

Estudo qualitativo dos vínculos

Reações nos vínculos de estruturas bidimensionais

Saiba mais

Graus de liberdade

Exemplo

A função do vínculo é restringir alguns graus de liberdade. Portanto, os vínculos em estruturas (em equilíbrio estático) podem ser classificados em função do número de graus de liberdade existentes.

Teoria na prática

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

Você chegou ao final do módulo 1!

MÓDULO 2

Introdução

Conceitos de força e de momento de uma força

Conceito matemático de força

A força é uma grandeza vetorial (representada por um vetor) e, por isso, apresenta as seguintes características: módulo (ou intensidade), direção (linha de ação da força) e sentido.

Você sabia

Forças (cargas) concentrada e distribuída

Atenção

Força escrita em função de suas componentes retangulares

A força é uma grandeza vetorial e, por isso, pode ser representada por suas componentes retangulares x, y e z.

Força no plano escrita em função de suas componentes retangulares

F → = F x . i + F y . j

F x = F . cos θ e F y = F . s e n θ

t g θ = F y F x → θ = a r c t g F y F x

F → = F . cos θ . i + F . s e n θ . j

F x 2 + F y 2 = F 2

Atividade

F x = F . cos θ e F y = F . s e n θ

F x = 100 . 0 , 8 = 80 N e F y = 100 . 0 , 6 = 60 N

F → = F . c o s θ . i + F . s e n θ . j

F → = 80 . i + 60 . j

Força no espaço escrita em função de suas componentes retangulares

cos θ x = F x F → F x = F . cos θ x

cos θ y = F y F → F y = F . cos θ y

cos θ z = F z F → F z = F . cos θ z

Atenção

F → = F . cos θ x . i + F . cos θ y . j + F . cos θ z . k

Atividade

F x = F . cos θ x → F x = 10000 . 2 2 = 7071 N

F y = F . cos θ y → F y = 10000 . 3 . 2 10 = 4243 N

F z = F . cos θ z → F z = 10000 . 2 2 5 = 5657 N

F → = F . cos θ x . i + F . cos θ y . j + F . cos θ z . k

F → = 7071 . i + 4243 . j + 5657 . k

Resultante de forças

R → = ∑ F i → → R → = ∑ F x . i + ∑ F y . j + ( ∑ F z ) . k

Atenção

F 1 - F 2 ≤ R ≤ F 1 + F 2

Atividade

R → = ∑ F i → → R → = ∑ F x . i + ∑ F y . j + ( ∑ F z ) . k

∑ F x = 20 - 50 = - 30 N

∑ F y = 80 - 20 = 60 N

∑ F z = 40 N

R → = - 30 . i + 60 . j + 40 . k

Momento de uma força em relação a um ponto

M → = r → × F →

M → = i j k r x r y r z F x F y F z

Atenção

Atividade

M → = i j k 1 2 5 10 20 30 = 60 i + 20 k + 50 j - 20 k - 30 j - 100 i = - 40 i + 20 j + 0 k

Equilíbrio estático de um corpo rígido

R → = ∑ F i → = 0 → e M→ = ∑ M→i = 0→

∑ F x = 0 ∑ F y = 0 ∑ F z = 0 ∑ M x = 0 ∑ M y = 0 ∑ M z = 0

∑ F x = 0 ; ∑ F y = 0 e ∑ F z = 0

∑ M x = 0 ; ∑ M y = 0 e ∑ M z = 0

∑ F x = 0 ; ∑ F y = 0 e ∑ M z = 0

λAB→ = B - AAB→ = ( xB - xA; yB - yA; zB - zA)AB→

AB→ = ( xB - xA)2 + (yB - yA)2 + (zB - zA)2

$\vec{F} = F_{x} . i + F_{y} . j$

$F_{x} = F . \cos θ e F_{y} = F . s e n θ$

$t g θ = \frac{F_{y}}{F_{x}} \to θ = a r c t g (\frac{F_{y}}{F_{x}})$

$\vec{F} = F . \cos θ . i + F . s e n θ . j$

${F_{x}}^{2} + {F_{y}}^{2} = F^{2}$

$F_{x} = F . \cos θ e F_{y} = F . s e n θ$

$F_{x} = 100 . 0, 8 = 80 N e F_{y} = 100 . 0, 6 = 60 N$

$\vec{F} = F . c o s θ . i + F . s e n θ . j$

$\vec{F} = 80 . i + 60 . j$

$\cos θ_{x} = \frac{F_{x}}{F} \to F_{x} = F . \cos θ_{x}$

$\cos θ_{y} = \frac{F_{y}}{F} \to F_{y} = F . \cos θ_{y}$

$\cos θ_{z} = \frac{F_{z}}{F} \to F_{z} = F . \cos θ_{z}$

$\vec{F} = F . \cos θ_{x} . i + F . \cos θ_{y} . j + F . \cos θ_{z} . k$

$F_{x} = F . \cos θ_{x} \to F_{x} = 10000 . \frac{\sqrt{2}}{2} = 7071 N$

$F_{y} = F . \cos θ_{y} \to F_{y} = 10000 . \frac{3 . \sqrt{2}}{10} = 4243 N$

$F_{z} = F . \cos θ_{z} \to F_{z} = 10000 . \frac{2 \sqrt{2}}{5} = 5657 N$

$\vec{F} = F . \cos θ_{x} . i + F . \cos θ_{y} . j + F . \cos θ_{z} . k$

$\vec{F} = 7071 . i + 4243 . j + 5657 . k$

$\vec{R} = \sum_{} \vec{F_{i}} \to \vec{R} = (\sum_{} F_{x}) . i + (\sum_{} F_{y}) . j + (\sum_{} F_{z}) . k$

$|\begin{matrix} F_{1} - & F_{2} \end{matrix}| \leq R \leq |\begin{matrix} F_{1} + & F_{2} \end{matrix}|$

$\vec{R} = \sum_{} \vec{F_{i}} \to \vec{R} = (\sum_{} F_{x}) . i + (\sum_{} F_{y}) . j + (\sum_{} F_{z}) . k$

$\sum_{} F_{x} = 20 - 50 = - 30 N$

$\sum_{} F_{y} = 80 - 20 = 60 N$

$\sum_{} F_{z} = 40 N$

$\vec{R} = - 30 . i + 60 . j + 40 . k$

$\vec{M} = \vec{r} \times \vec{F}$

$\vec{M} = |\begin{matrix} i & j & k \\ r_{x} & r_{y} & r_{z} \\ F_{x} & F_{y} & F_{z} \end{matrix}|$

$\vec{M} = |\begin{matrix} i & j & k \\ 1 & 2 & 5 \\ 10 & 20 & 30 \end{matrix}| = 60 i + 20 k + 50 j - 20 k - 30 j - 100 i = - 40 i + 20 j + 0 k$

$\vec{R} = \sum_{} \vec{F_{i}} = \vec{0}$ e $\vec{M} = \sum_{} {\vec{M}}_{i} = \vec{0}$

$\sum_{} F_{x} = 0$

$\sum_{} F_{y} = 0$

$\sum_{} F_{z} = 0$

$\sum_{} M_{x} = 0$

$\sum_{} M_{y} = 0$

$\sum_{} M_{z} = 0$

$\sum_{} F_{x} = 0; \sum_{} F_{y} = 0 e \sum_{} F_{z} = 0$

$\sum_{} M_{x} = 0; \sum_{} M_{y} = 0 e \sum_{} M_{z} = 0$

$\sum_{} F_{x} = 0; \sum_{} F_{y} = 0 e \sum_{} M_{z} = 0$

$λ_{\vec{A B}} = \frac{B - A}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})}{|\begin{matrix} \vec{A B} \end{matrix}|}$

$|\begin{matrix} \vec{A B} \end{matrix}| = \sqrt{{(x_{B} - x_{A})}^{2} {+ (y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}}$

$λ_{\vec{A B}} = \frac{B - A}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})}{|\begin{matrix} \vec{A B} \end{matrix}|}$

$λ_{\vec{A B}} = \frac{(4, 3, 9) - (1, 3, 5)}{|\begin{matrix} \vec{A B} \end{matrix}|} = \frac{(3, 0, 4)}{|\begin{matrix} \vec{A B} \end{matrix}|}$

$|\begin{matrix} \vec{A B} \end{matrix}| = \sqrt{{(x_{B} - x_{A})}^{2} {+ (y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}} = \sqrt{{(3)}^{2} {+ (0)}^{2} + {(4)}^{2}} = \sqrt{9 + 0 + 16} = \sqrt{25} = 5$

$λ_{\vec{A B}} = \frac{(3, 0, 4)}{5}$

$\vec{F} = λ_{\vec{A B}} . F$

$\vec{F} = \frac{(3, 0, 4)}{5} . 100 = (3, 0, 4) . 20 = (60, 0, 80) N$

$(\sum_{} F_{x} = 0, \sum_{} F_{y} = 0 e \sum_{} M_{z} = 0)$

$(\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} F_{z} = 0, \sum_{} M_{x} = 0, \sum_{} M_{y} = 0 e \sum_{} M_{z} = 0)$ .

$\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} M_{z} = 0$ ,

$\sum_{} F_{x} = 0, \sum_{} F_{y} = 0, \sum_{} M_{z} = 0$