Descrição
Principais conceitos, técnicas e orientações com relação ao estabelecimento do campo elétrico e do campo magnético em cabos condutores da linha de transmissão. Caracterizações importantes sobre o efeito corona e o efeito Joule no sistema.
PROPÓSITO
Apresentar as premissas e considerações necessárias para calcular o campo elétrico e o campo magnético em uma linha de transmissão, entender como se estabelecem os efeitos corona e Joule e assim estimar a temperatura superficial e perdas devido a esses efeitos.
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e uma calculadora ou use a calculadora de seu smartphone/computador.
OBJETIVOS
Módulo 1
Reconhecer as principais estratégias para os cálculos dos campos elétrico e magnético em cabos de linhas de transmissão
Módulo 2
Identificar os efeitos relacionados à radiofrequência e ao efeito corona
Módulo 3
Analisar os cálculos da temperatura superficial em cabos e das perdas devido aos efeitos Joule e corona
O especialista fala sobre a visão geral sobre os cálculos nos cabos de linhas de transmissão e uma breve revisão acerca da análise de circuitos, trazendo a visão geral sobre o que deve ser considerado acerca do campo elétrico e do campo magnético nestes tipos de cabos e sobre circuitos monofásicos e circuitos trifásicos.
MÓDULO 1
Reconhecer as principais estratégias para os cálculos dos campos elétrico e magnético em cabos de linhas de transmissão
O especialista fala sobre a visão geral dos possíveis circuitos equivalentes de uma linha de transmissão - trazer uma visão geral de modelos para linhas curtas, médias e longas.
Introdução
Para compreender como o campo elétrico e o campo magnético se estabelecem nos cabos condutores das linhas de transmissão, é necessário considerar alguns conhecimentos técnicos prévios, como as principais premissas utilizadas nas análises de circuitos monofásicos e de circuitos trifásicos, além dos conhecimentos de eletromagnetismo.
Além disso, é necessário compreender as analogias e circuitos equivalentes, tomados para cálculo dessas relações tão importantes para o funcionamento da linha e do próprio sistema. Dessa forma, iniciamos nossa análise entendendo como deve ser calculada a indutância em linhas de transmissão e, em seguida, a capacitância nelas, para contextualização. No fim desse tema, é feita também a análise qualitativa do funcionamento da linha.
Indutância da linha de transmissão
A indutância da linha de transmissão é um dos principais aspectos a ser considerado na modelagem da corrente alternada (CA) e, geralmente, é definida em unidade por comprimento, ou seja, em Henry por quilômetro (H/km).
Relembrando
É importante relembrar que o tipo do modelo a ser usado dependerá, logicamente, do tipo de estudo e/ou projeto conduzido e que existem de fato diferenças importantes, referentes às linhas de corrente alternada, que devem ser consideradas perante a escolha da transmissão em corrente contínua (CC), por exemplo.
Especificamente com relação ao cálculo, Monticelli e Garcia (2003) ressaltam que a indutância depende do comprimento da linha, o que inclusive explica o porquê de, em distâncias acima de 1.000 km, as linhas de transmissão em corrente contínua poderem ser melhores opções, embora este comprimento deva ser analisado sob a ótica de uma série de fatores e parâmetros, dependendo também de outras características mais específicas do projeto.
O fluxo concatenado, a partir da Lei de Faraday, pode ser utilizado para expressar a indutância, tal que a seguinte relação é válida:
(1)
Além disso, a indutância pode ser expressa diretamente a partir da tensão induzida:
(2)
Para as linhas, deve-se considerar as diferenças entre os fluxos e os fluxos concatenados e possíveis arranjos nos quais o fluxo concatenado é maior, juntamente com a tensão induzida, por exemplo.
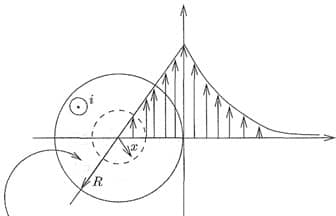
Com relação ao fluxo concatenado com a corrente do condutor, adicionalmente, considere a figura adiante, que representa a distribuição do fluxo magnético em um condutor cilíndrico de raio R, percorrido por uma corrente de intensidade i e que é dada como função da distância até o eixo desse condutor:
Assim, a partir da Lei de Ampére (equação de Maxwell), é possível calcular as componentes interna e externa do fluxo concatenado. Essa equação é dada como a seguir, para γ sendo uma curva fechada, como no caso da curva representada por uma circunferência por exemplo:
(3)
O campo magnético, considerando a situação proposta pela Figura 1, é dado por:
(4)
E a densidade do fluxo magnético:
(5)
Desenvolvendo-se a partir dos fluxos, obtém-se que a componente interna da indutância neste caso é:
[H/m](6)
E a externa:
[H/m](7)
Por outro lado, considerando-se para análise e modelagem os casos de raio reduzido para o condutor, tem-se a seguinte relação válida para a indutância, tomando a relação de :
[H/m](8)
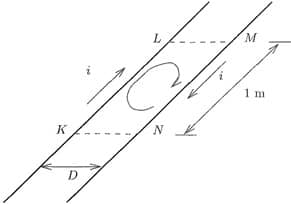
Dessa forma, é possível contextualizar melhor e definir, a este ponto, a indutância para a linha bifilar, tal como mostra a equação a seguir:
[H/m](9)
Sendo está representada como mostra o desenho adiante:
Analisando-se, então, a indutância em uma linha trifásica, tem-se que as relações entre os fluxos concatenados com as correntes nas fases, i1, i2 e i3, poderão ser estabelecidas na forma matricial:
(10)
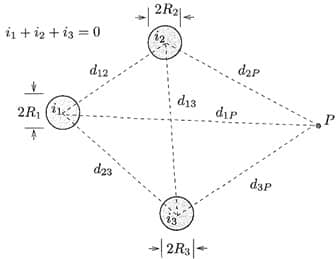
Sendo o espaçamento entre os condutores de geometria bem definida e distâncias iguais, como no caso de um triângulo equilátero, a matriz da Equação 10 será uma matriz diagonal, com os mesmos elementos na diagonal principal. A figura a seguir, por outro lado, apresenta um exemplo mais geral, considerando um arranjo genérico trifásico:
De maneira geral, definem-se os fluxos concatenados pelas seguintes equações:
(11.a)
(11.b)
(11.c)
Definindo-se a matriz indutância da linha e considerando o somatório das correntes nulo, tem-se:
(12)
Se a linha trifásica for equilátera, como no caso da geometria do triângulo equilátero:
(13)
Existe ainda a possibilidade de realizar a transposição da linha de transmissão, de forma a transformar uma dada linha, em outra configuração original qualquer, não simétrica, em uma linha equilátera.
Por outro lado, caso diferentemente do exposto até então, utilizem-se vários condutores por fase, o cálculo modificará e deve-se levar em conta desprezar ou não o efeito pelicular (também conhecido como efeito skin)
MONTICELLI; GARCIA, 2003
Para o cálculo do fluxo concatenado em um dado condutor a na fase 1, por exemplo, para um arranjo de dois condutores por fase, tem-se:
(14)
Tomando-se, de forma a simplificar a análise, que o ponto P está no infinito e que o somatório das três correntes é zero, tem-se:
(15)
Caso tome-se que D >> d, a seguinte expressão é válida:
(16)
E, analogamente, para as demais fases:
(17)
Mais, considerando-se a transposição, obtém-se a indutância por fase de:
(18)
Vamos ver um exemplo:
Tomando como exemplo as linhas de transmissão CA de Itaipu, é possível traçar alguns passos básicos para o cálculo da indutância por unidade de comprimento do circuito trifásico. Assim, inicia-se buscando qual o tipo de condutor e seu o valor da distância geométrica própria (Ds), que levará em conta se são usados diversos fios encordoados, por exemplo. Em seguida, deve-se verificar o tipo de agrupamento por fase e transformar o circuito, no caso a linha, em um circuito equilátero equivalente, de forma que o espaçamento equivalente é dado por , fazendo D >> d. Por último, o cálculo da indutância por fase e por unidade de comprimento é possível (MONTICELLI; GARCIA, 2003).
Adiante, no próximo subtópico, você verá as principais premissas acerca da capacitância na linha de transmissão e os cálculos com relação a esta e o campo elétrico estabelecido.
Capacitância da linha de transmissão
Faremos, agora, um resumo do cálculo da capacitância na linha e, para isto, é primordial relembrar a Lei de Gauss, que estabelece que:
(19)
Sendo o vetor do campo elétrico na superfície, o vetor normal a este campo, ρ a densidade volumétrica ou superficial de carga, dV o elemento diferencial do volume e q a carga total internamente em S. Considerando inicialmente a distribuição de carga em um condutor, define-se o seguinte campo elétrico, com sendo a constante do meio e r a distância:
(20)
A capacitância por unidade de comprimento é:
(21)
Sendo que λ é a densidade linear de carga e V o potencial do condutor, que é dado conforme a seguinte equação:
(22)
Na equação anterior, P é um ponto na superfície do condutor analisado e R é seu raio.
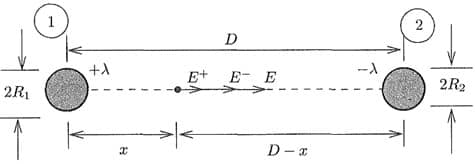
Para continuarmos nossa análise, considere uma linha bifilar, assim como fizemos na análise de indutância, na qual são usados dois condutores, como mostra a figura adiante:
A diferença de potencial neste caso é calculada como:
(22)
A distância entre o eixo do condutor 1 e o ponto 1, por exemplo, é dada por r1p1 e assim por diante. Já com relação a um dado ponto P, distante desses condutores, define-se:
(23)
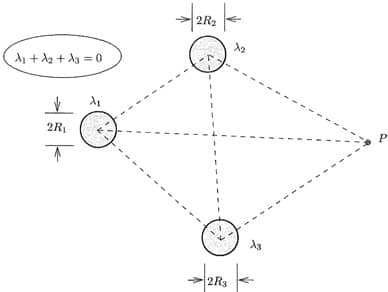
Já para linhas trifásicas, considere o exemplo do seguinte arranjo de geometria genérica e utilizando somente um condutor por fase, como mostra a figura:
Neste caso, a relação entre as densidades de carga, os potenciais e as capacitâncias é dada pela seguinte equação matricial:
(24)
É importante destacar que, da mesma forma que ocorre com a indutância nos condutores no arranjo trifásico, existem simplificações válidas para o caso de um arranjo equilátero. Assim, considerando, por exemplo, que a soma das densidades de carga em cada uma das fases é nula:
(25)
E, por último nesta parte, considerando então o arranjo equilátero onde D representa a distância entre condutores:
(26)
Vamos ver um exemplo:
Neste exemplo, vamos entender quais são as principais influências da terra no cálculo da capacitância. Para isso, é possível utilizar o método das imagens, que lida com as condições de contorno dadas pelas cargas que são induzidas na superfície da terra, comparando-as de forma que é estabelecido que elas são as mesmas de um par de condutores fictícios atribuídos, em posição simétrica à superfície (MONTICELLI; GARCIA, 2003). Assim, considerando que os raios dos condutores são desprezíveis, ou seja, R ‹‹ D e ignorando-se a presença da terra (o que implica que a distância (H) a terra é muito maior que a distância entre condutor), ou seja, H ›› D em Faradays por metro:
Se os raios são iguais, a equação anterior pode ainda ser simplificada.
Análise qualitativa do funcionamento da linha de transmissão
Como já foi brevemente mencionado no início do módulo, você verá agora os principais aspectos do funcionamento da linha, considerando ainda o conhecimento teórico adquirido até o momento para a compreensão desta teoria diretamente ligada à prática.
Iniciamos, então, pela análise qualitativa e uma possível análise quantitativa, para entendimento de perdas, que será realizada no fim do Módulo 3.
Quando tratamos da linha do ponto de vista qualitativo, é importante considerar o processo de energização da linha.
Dessa forma, considere então uma linha de transmissão ideal, formada por dois condutores metálicos retilíneos completamente isolados, suficientemente distantes do solo e/ou de estruturas adjacentes.
Assim, sendo uma linha ideal, a resistência elétrica desses condutores será considerada nula, o dielétrico formado é perfeito e não existirão perdas a serem computadas.
Capacidade
- C é definida em F/km
Indutância
- L é definida em H/km
O seguinte circuito equivalente representa de forma aproximada a linha bifilar descrita, juntamente com um ponto de dissipação de energia, representado pela resistência R2:
No momento de em que a chave se fecha (t = 0), tem-se que a tensão V é igual a v1.
Além disso, perceba que, no primeiro trecho, a tensão V só será vista na reatância capacitiva, após um dado período Δt e a corrente na reatância indutiva não atingirá de forma instantânea o valor de Io (corrente de carga na linha). Já no 2° trecho do circuito equivalente, percebe-se que a tensão V só estará na reatância capacitiva após um período de 2Δt e tem-se o momento em que a corrente é igual à corrente de carga na linha. Adicionalmente, tem-se que, após um dado tempo, (finito) a tensão chegará ao receptor, o que implica que decorreu de fato um tempo entre o momento no qual aplicou-se a tensão V na fonte do sistema e com relação ao instante no qual essa tensão pode ser “sentida” e medida no receptor (FUCHS, 1977).
Assim, a velocidade dessa propagação no sistema (v) é dada em função do comprimento (Δx) e do tempo (Δt), tal que:
(27)
Já a carga nesse trecho é calculada em função da capacitância:
(28)
Define-se a corrente no trecho como:
(29)
De forma que a relação tensão/corrente é:
(30)
Sendo Z0 a impedância natural da linha, definida por essa relação tensão/corrente.
Lembre-se que as cargas elétricas em movimento são as responsáveis pelo surgimento de campos magnéticos e que sua própria existência, por outro lado, já permite o surgimento dos campos elétricos. Quando uma linha de transmissão é energizada, portanto, estabelece-se campos elétricos e magnéticos do transmissor ao receptor, que se propagam ao longo deles (FUCHS, 1977).
A força eletromotriz induzida (FEM), neste caso, é:
(31)
Considerando-se que o tempo pode ser expresso em função do comprimento e da velocidade v, tem-se a seguinte expressão para FEM:
(32)
Adicionalmente, sabe-se que essa FEM deverá ser neutralizada pela própria fonte de tensão (V) utilizada para a energização da linha, para que se tenha de fato a circulação da corrente I0 através do condutor do cabo, basicamente. Assim, tem-se que:
[V](33)
Ou ainda:
[Ω](34)
Ou seja, a impedância natural foi definida de duas formas distintas (rever Equação 30), dependendo somente do meio no qual a linha de transmissão estiver e de suas dimensões físicas.
A partir dessas relações, define-se novamente a velocidade com a qual tanto o campo elétrico quanto o magnético se propagam na linha de transmissão, como mostra a equação seguinte, similarmente ao que foi feito na Equação 27:
(35)
Agora, retornaremos novamente ao cálculo da indutância e da capacitância, nesse caso, estimando esses parâmetros para uma linha com dois condutores, os quais podem estar tanto no ar quanto no vácuo. Como anteriormente, desprezou-se novamente a presença da terra, no caso da capacitância e do efeito do fluxo magnético interno no condutor, no caso do cálculo da indutância:
[H/km](36)
[F/km](37)
Ao correlacionar as equações 36 e 37, inserindo-as no cálculo da velocidade na Equação 35, obtém-se o valor da velocidade de propagação da luz no vácuo, com o valor de 3.105 km/s. Com isso, torna-se possível concluir que a velocidade de propagação depende, principalmente, do meio de propagação e, por consequência, do meio no qual a linha de transmissão está instalada. Por esses mesmos motivos, observa-se que, em linhas subterrâneas, essa velocidade será diferente e bem mais baixa.
Além disso, na prática, para linhas reais nas quais o fluxo interno dos condutores também não é desprezível, essa velocidade será um pouco menor, sendo importante lembrar que, nesse caso, considera-se perdas reais (FUCHS, 1977). Tais perdas elétricas na linha também reduzem a velocidade de propagação e podem ser representadas por elementos como resistores, capacitores e indutores, o que ficará mais claro no Módulo 3.
Adicionalmente, com relação à impedância natural da linha é possível, substituindo-se novamente os valores obtidos nas Equações 36 e 37, obter a seguinte equação:
(38)
Note, por meio da análise da Equação 38, que a impedância natural não depende do comprimento da linha e de outras características físicas como o meio no qual se encontra, a distância entre condutores e seus raios. Perceba, então, que a impedância natural da linha é constante e, assim, considerada uma grandeza característica da linha. Mais ainda, percebe-se que a corrente será constante, pois a seguinte relação obtida reescrevendo-se as equações de tensão, corrente e impedância natural é válida:
(39)
Ou seja, a corrente de carga em uma dada linha já energizada, sujeita à excitação por uma fonte de tensão constante, também não dependerá de seu comprimento. Embora isso possa soar estranho, à primeira vista, ao analisarmos percebemos que não era possível ser diferente, visto que ao fluir, essa corrente não terá "percepção" nem do quanto a linha é grande (ou pequena) e/ou em que ponto se finda.
Relações de energia
Com relação à energia, sabe-se basicamente que a cada intervalo de tempo, necessário para energizar um dado comprimento da linha, a fonte fornecerá a essa a mesma quantidade de energia (dada por VI0Δt). Essa energia, numa linha ideal, logicamente não será dissipada.
Vamos ver agora mais um pouco sobre isso e iniciar a análise das percepções acerca das perdas?
Lembre-se, antes de tudo, que o campo elétrico e o magnético possuem capacidade de armazenar energia possibilitando definir as seguintes relações:
[W](40)
Adicionalmente, como o armazenamento é simultâneo, define-se:
[W](41)
Com isso, é possível concluir previamente que a energia fornecida pela fonte foi de fato armazenada, entretanto não sabemos qual a fração para cada campo até o momento
FUCHS, 1977
Para esclarecer tal fato, são realizadas algumas análises e obtém-se a seguinte expressão, que nos revela que a quantidade de energia armazenada nos campos é a mesma:
(42)
Na prática, sabe-se ainda que esse processo de armazenamento durará de forma indefinida, caso seja considerado, idealmente, que a linha possui comprimento infinito. Contudo, estabelecendo-se então para entender a análise real que a linha possua um dado comprimento l, em metros e que há um dissipador de energia no sistema, representado pelo resistor R2, de forma que seu módulo seja igual ao da impedância natural, obtém-se com relação à corrente elétrica:
(43)
Adicionalmente, considerando que na terminação da linha não haverá campos a serem armazenados, toda a energia é dissipada em R2. Nesse caso, a corrente mantém-se constante, independentemente do comprimento da linha, o que é plausível para a análise considerando-a infinita:
[W](44)
Agora, vamos analisar algumas outras possíveis situações distintas e, para isso, considere inicialmente que a linha possui resistência terminal maior do que Z0. Nesse caso, tem-se uma situação de excesso de energia junto ao terminal da linha e observa-se que há um novo estado de equilíbrio já que, logicamente, essa energia não é simplesmente destruída. Além disso, perceba que uma redução da corrente na linha proporciona também redução no campo armazenado e ele não é capaz de armazenar o excedente mencionado, cedendo ainda o que possui, o que explica por que a energia possui como destino o campo elétrico.
Em outro caso ainda mais extremo, considerando que R2 tende a infinito, tem-se dois fatos principais: a corrente vai a zero e o campo elétrico novamente é responsável por armazenar toda a energia novamente. A partir disso, é possível obter que, em uma linha ideal aberta (aproximação da resistência infinita), a tensão no receptor será o dobro da que fora aplicada e se propaga.
Caso, por outro lado, a resistência terminal seja menor que a impedância característica, é estabelecido um novo estado de equilíbrio, que somente é atingido na prática caso a deficiência de energia no terminal seja suprida pela própria linha, por meio da energia armazenada no processo de energização da linha pela fonte. Devido ao aumento no valor à corrente e considerando que agora quem cede energia é o campo elétrico, percebe-se uma redução na tensão V2 (receptor).
Assim como analisamos anteriormente, caso tenha-se o extremo no qual R2 seja nulo ou extremamente baixo, duas situações novamente podem se estabelecer:
- A tensão no receptor é nula e se propaga ao transmissor.
- Há um aumento na corrente no receptor, que se propaga também (FUCHS, 1977).
Ademais, para determinar o valor dessa corrente, relembre a relação de cessão energética ao campo magnético e torna-se possível perceber que quando a linha estiver em curto-circuito (resistência nula) a corrente crescerá no receptor até dobrar seu valor, com relação à corrente de linha I0.
Ondas viajantes
O conceito de ondas viajantes é de extrema importância no entendimento do funcionamento da linha e, para entendê-lo, considere novamente a energização dessa linha, com circuito equivalente análogo.
Considera-se agora, então, que duas ondas partirão do transmissor, uma de tensão (com uma dada amplitude V) e outra de corrente (com a amplitude I0) e ambas com velocidades v. Essas ondas, por fim, poderão ser do tipo diretas ou refletidas, sendo ambas polarizadas.
Para entender como isso ocorre, retornaremos aos casos anteriores das diferentes resistências terminais atribuídas.
Começando pelo caso no qual a linha tem que R2 é maior que a impedância natural, a onda de tensão refletida possuirá o mesmo sinal da onda de tensão incidente e a tensão que resulta é maior do que a da incidente. A onda que chega ao receptor é a incidente, enquanto a que sai dele é a refletida. Por outro lado, caso a resistência terminal seja inferior à impedância natural, a onda da tensão é refletida com sinal contrário ao da incidente, o que leva à tensão diminuir e, com relação à corrente, sabe-se que ela se reflete com o mesmo sinal, aumentando no fim das contas. Por último caso, se a resistência em questão tiver o mesmo valor da impedância analisada, tanto as ondas refletidas de tensão quanto de corrente serão nulas e, assim, os valores de tensão e de corrente mantêm-se (FUCHS, 1977).
Mais ainda, considerando que ondas refletidas possuem as mesmas propriedades das ondas incidentes, a seguinte relação é válida:
(45)
Além disso, em qualquer ponto no qual a resistência terminal vista seja diferente da impedância característica, é válido que:
(46)
Adicionalmente, levando-se em conta as amplitudes dessas ondas refletidas, utilizando os seguintes coeficientes de reflexão
(47.1)
(47.2)
tem-se as próximas amplitudes, para tensão e para a corrente, respectivamente:
Atenção
É fundamental salientar que foi analisado o comportamento das ondas da tensão e corrente durante a primeira circulação do transmissor ao receptor, incluindo o movimento e comportamento das ondas de tensão e correntes que foram refletidas, em função das condições existentes no receptor.
Um ponto importante também é que considerando o uso da fonte ideal, por exemplo, as ondas verão uma impedância diferente de Zo, o que faz com que elas deem origem a um novo par de ondas refletidas, que vão se sobrepor aos incidentes no transmissor.
Lembrando-se que essas últimas as que partiram do receptor como ondas refletidas e seus sinais e valores dependem do valor relativo da impedância da fonte (FUCHS, 1977., p. 67).
Depois dessas análises, é perceptível, de fato, o caráter nitidamente transitório das tensões e correntes, que variam em torno de seus valores em regime permanente. Sendo ainda tanto a linha quanto as fontes ideais, o regime permanente só é atingido, tipicamente, na condição de t → ꝏ. Já, por outro lado, no caso de linhas reais, sabe-se que a energia que é dissipada na resistência dos condutores da linha possui o caráter de um “amortecedor energético”, capaz de reduzir levemente os módulos de tensões e correntes, o que faz com que a transição do funcionamento da linha em regime permanente ocorra de forma significativa.
Por fim, até mesmo para motivá-lo, ficou claro que esse estudo possui grande aplicação em análises de surtos e da ocorrência de sobretensões em sistemas elétricos de potência, nos quais para facilidade de raciocínio, é comum empregarmos uma fonte de tensão constante, por exemplo.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Identificar os efeitos relacionados à radiofrequência e ao efeito corona
Introdução
O especialista fala sobre o método analítico para cálculo da radiointerferência sob condições de chuva - outras formas de análise complementares.
A ocorrência de radiointerferência e de certos efeitos relacionados ao efeito corona tratam-se, em geral, de efeitos especiais relacionados à transmissão de energia por meio de sistemas aéreos.
Vamos, então, iniciar nosso estudo analisando as questões acerca da resistência à corrente alternada, ainda nesse tópico, para depois passarmos para os dois tópicos principais:
- Principais pontos sobre o efeito corona.
- Radiointerferência (RI).
Funcionando então em corrente alternada, sabe-se que em cada condutor vai existir, além da queda de tensão de caráter ôhmico, uma tensão (ou força eletromotriz) induzida devido ao fluxo magnético alternado (para mais detalhes ver as Equações 31 e 32).
Assim, sendo a queda de tensão ao longo de uma dada secção transversal do condutor a mesma em todos os pontos, embora os enlaces do fluxo não sejam, com pontos mais próximos do centro da secção, por exemplo, mais enlaçados, define-se que as correntes devem ser maiores nos pontos mais próximos da superfície, de forma a compensar essa diferença e igualar, assim, as quedas de tensão
CAMARGO, 2006
Com isso, percebe-se que a densidade da corrente é superior nos pontos periféricos e este é o fenômeno caracterizado pelo efeito pelicular (ou efeito skin), que leva a efeitos práticos negativos, como um aumento da resistência do condutor e diminuição de sua reatância interna.
Surge, assim, a necessidade de se definir o quão é desigual essa distribuição das correntes e, define-se, portanto, o parâmetro de profundidade de penetração, sendo:
Poderá ser necessário ainda, ao longo do projeto do sistema de transmissão, o cálculo exato desse efeito pelicular.
Saiba mais
É interessante que você saiba, a título de curiosidade, que isso envolve as funções de Bessel e resoluções de equações diferenciais características do problema. Ademais, sabe-se que, para determinação de fato da resistência à corrente alternada, deve-se ter em mente o material e tipo de cabo utilizado, por exemplo.
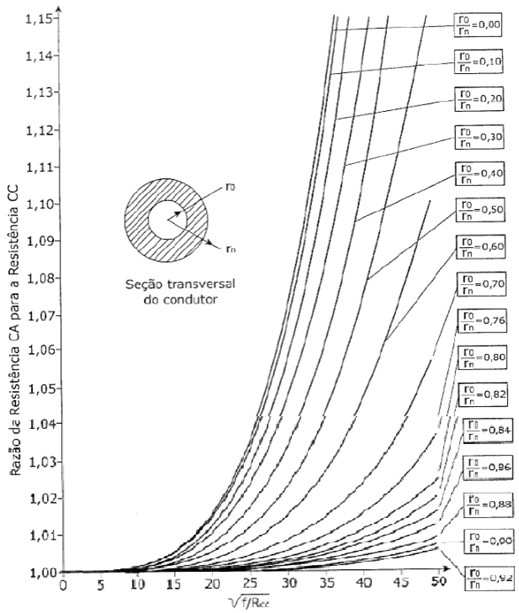
Vamos ver um exemplo:
Considerando um cabo de aço, tem-se como exemplo as seguintes curvas de relações entre a resistência à corrente alternada e à corrente contínua, conforme apontado em ALCOA (1960), mediante a razão com a frequência:
Efeito corona
Caso a tensão na linha aumente de forma significativa até alcançar um valor no qual o ar torna-se capaz de envolver o condutor e esse se torna ionizado, devido à força elétrica estabelecida na superfície desse condutor, que excedeu um certo valor limite.
Além disso, sabe-se que a camada ionizada aumenta o diâmetro até um ponto no qual as forças elétricas deixam de ser capazes de gerar mais ionização. Esse tipo de descarga elétrica descrita, bem como os efeitos relacionados a ela, é definida como efeito corona.
Além disso, tem-se que esse fenômeno ocorre devido ao campo elétrico na superfície do condutor ter superado a capacidade disruptiva do ar (CAMARGO, 2006).
Entre as principais consequências do efeito corona, tem-se:
- Ocorrência de eflúvios visíveis
- Formação de certas ondas de rádio ruído
- Perdas de energia e vibrações mecânicas
- Gases como o ozona
- Ruídos que podem ser ouvidos
Assim, matematicamente, o efeito corona se dá quando a seguinte relação ocorre:
(50)
Sendo E o campo elétrico na superfície do condutor e E0 a constante de capacidade disruptiva do ar, que pode ser dada por:
(51)
Em que T é a temperatura em Fahrenheit e P a pressão em polegadas de mercúrio, ou então considera-se diretamente 30 kV/cm, para condições típicas de temperatura e pressão.
Outro importante parâmetro para análise desse fenômeno, é compreender que existem momentos diferentes de "criticidade" e, desta forma, atribui-se o gradiente crítico visual ao momento de início da ocorrência das manifestações luminosas.
Esses estudos foram conduzidos por Peek, na ocasião, que apresentou a seguinte relação desse gradiente:
[kV/cm](52)
Posteriormente, Miller sugeriu que esse poderia ser definido como:
[kV/cm](53)
Podendo ser utilizada para condutores múltiplos, com correção do diâmetro e considerações e aproximações acerca do gradiente na superfície (FUCHS, 1977). Já o gradiente médio por subcondutor, nesses casos mais complexos, em que req é o raio de um condutor cilíndrico equivalente à carga de Q C/km, tem-se o seguinte gradiente:
[kV/cm](54)
Vamos relembrar, agora, o cálculo da capacitância na linha de transmissão e, com isso, obtém-se a seguinte relação para o gradiente crítico, válida para a maior parte das análises:
[kV/cm](55)
sendo m o fator de superfície para representar fatores externos que podem afetar a forma como o efeito corona é estabelecido e com δ para representar a pressão atmosférica relativa, que vale:
(56)
No cálculo da pressão, a temperatura deve ser utilizada em Kelvin e h é a altitude média local.
Exemplo
Exemplo prático: O fator de superfície geralmente flutua, para a maior parte dos casos, entre 0,6 e 0,8 e, além disso, ressalta-se que, na prática, um aumento na temperatura e na altitude poderá refletir em grande parte dos casos na diminuição do gradiente crítico visual.
A seguir, você verá, com mais detalhes, o que ocorre em consequência da radiointerferência em uma linha de transmissão.
Radiointerferência
A radiointerferência (RI) é definida no contexto como um tipo de distúrbio indesejável, que atua na faixa de radiofrequência, de 500 kHz até 1600 kHz (que corresponde à faixa AM).
Além disso, um dos principais fenômenos ou causa desse efeito é o próprio efeito corona, ao produzir pulsos de corrente e de tensão nos condutores da linha, com espectro de frequência na faixa de radiofrequência.
Outro exemplo de causa da radiofrequência é a presença de irregularidades na superfície dos condutores e/ou partículas sólidas que se aderem aos cabos, capazes de provocar pulsos de corrente, que leva à ocorrência de campos magnéticos. Esses campos, por sua vez, interferem diretamente na qualidade da recepção de sinais de rádio e, dessa forma, quando é feito o projeto de um sistema de transmissão essas questões devem ser consideradas, além da medição constante de determinados trechos acerca de verificar se de fato a linha funciona como projetado, com relação à radiofrequência (CAMARGO, 2006; LEÃO, 2008).
Para afetar essa relação de radiofrequência, sabe-se ainda que quaisquer alterações nos seguintes parâmetros poderão levar a efeitos indesejados, como:
- Mudanças nas configurações dos condutores das linhas.
- Alterações no fator de superfície.
- Alterações em fatores diretamente ligados ao clima e ao solo como sua resistividade.
- Umidade relativa do ar.
- Velocidade do vento de quantidade de chuvas.
Além disso, deve-se considerar ainda a frequência da energia que é irradiada.
Mais ainda, deve-se ter em mente que ruídos, por exemplo, só serão vistos de fato após o funcionamento da linha e, para quantificar o quão alto eles podem ser estabelecidos, tem-se a seguinte equação:
(58)
Além disso, considerando-se a relação entre o ruído de uma emissora (S) e o funcionamento da linha (R), estabelece-se a seguinte relação sinal/ruído:
(59)
Para se ter uma ideia melhor na prática dessa relação, considere a seguinte tabela acerca da qualidade de percepção auditiva, em função de uma dada relação sinal/ruído:
| Relação sinal/ruído (dB) | Qualidade de percepção | Classe da percepção |
|---|---|---|
| 32 | Inteiramente satisfatória | A |
| 27 a 32 | Muito boa, ruído não oportuno | B |
| 22 a 27 | Boa, fundo ligeiramente evidente | C |
| 16 a 22 | Fundo muito evidente, voz humana facilmente compreensível | D |
| 6 a 16 | Voz humana inteligível, somente com imensa concentração, ruído de fundo muito evidente | E |
| < 6 | Voz humana ininteligível | F |
A Eletrosul, por exemplo, utiliza o valor de 24 dB. Assim, devem ser salientados dois aspectos principais quando tratamos do fenômeno de radiointerferência: o efeito corona, como já mencionado, especialmente considerando a operação em tensão acima de 100 kV e ocorrências como o centelhamento de cabos condutores, de isoladores e problemas relacionados a acessórios. Esse último fator poderá frequentemente ser eliminado dependendo do uso de algumas medidas próprias de correção. Além disso, o valor estimado para o nível de radiointerferência será um fator fundamental e básico para a realização do projeto de uma linha, como já ficou claro até aqui, sendo levado em consideração fatores como a configuração das linhas, por exemplo. Lembrando-se que, por consequência, esse nível influenciará, dadas as configurações, na largura da faixa de servidão, por exemplo, além de vários outros parâmetros.
Por fim, para se ter uma noção técnica maior das orientações propriamente ditas, sugere-se o conhecimento de NBR:
NBR 7875
acerca dos instrumentos de medição de radiointerferência (faixa de 0,15 até 30 MHz).
NBR 7876
que trata também da medição, mas mais especificamente acerca dos equipamentos e linhas de alta tensão.
NBR 15121
de 2004, destinada aos isoladores de alta tensão, com ensaio deles acerca da radiointerferência.
Dada então a importância dos níveis da radiointerferência, para se ter tais valores de forma mais detalhada sugere-se considerar basicamente os seguintes aspectos:
A análise do espectro de frequência - O espectro de frequência mostrará a variação do nível da radiointerferência nesses casos.
Perfil lateral utilizado - O perfil dá uma ideia da atenuação transversal, que depende da geometria utilizada na linha.
O uso de curvas de distribuição estatística - As curvas, por sua vez, permitirão a implementação prática da correlação com ocorrências climáticas.
Além disso, para medir-se, de fato, a radiointerferência é analisada por um receptor super-heteródino, capta-se este sinal e o insere em um amplificador de alta frequência.
Por fim, para o cálculo empírico da radiointerferência, é possível utilizar a seguinte relação:
(60)
Em que Ro é o valor de referência para uma dada distância de 30,5 m e as condições apresentadas no quadro a seguir são válidas:
| R0 | 34 dB ± 6, para linhas horizontais (valor médio e bom tempo) |
| 37 dB ± 6, para linhas verticais (valor médio e bom tempo) | |
| A | 146 para tempo bom |
| 120 para tempo ruim | |
| B | 40 para linhas horizontais |
| 32 para linhas verticais | |
| C | 1 quando f > 1 MHz |
| 0,5 quando f ≤ 1 MHz | |
| Emáx | Gradiente máximo em kV/cm |
| d | Diâmetro do condutor |
| D | Distância radial do condutor até a antena em m |
Lembre-se, então, que essa fórmula permite calcular o nível de rádio ruído, em decibéis, em uma dada frequência de referência.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Analisar os cálculos da temperatura superficial em cabos e das perdas devido aos efeitos Joule e corona
O especialista fala sobre estimação da temperatura máxima no condutor da linha de transmissão
Temperatura superficial
A temperatura superficial dos condutores é um parâmetro determinante para representar a capacidade de transporte da linha de transmissão, e capaz de representar efeitos em características, especialmente as eletromecânicas e metalúrgicas dos materiais dos condutores, além de levar a possíveis reduções de distâncias entre partes vivas e aterradas, por exemplo (SCHURIG; FRICK, 1930; DAVIDSON; DONOHO, 1969).
Sabe-se ainda que essa temperatura é resultado da interação do condutor com características elétricas do sistema e o próprio meio ambiente, tornando esse parâmetro de fato bastante aleatório, quando pensamos na própria dependência com as condições climáticas da região que é atravessada pela linha.
Além disso, ressalta-se que o conhecimento do valor da temperatura superficial em tempo real e a previsão do seu valor máximo, em horizontes que podem variar de horas até dias, irá facilitar o próprio estabelecimento da confiabilidade do sistema, e sua manutenção, sob o ponto de vista de estratégias importantes como o planejamento, o projeto, a operação e a manutenção das linhas (MOREIRA, 2006).
A maioria das linhas é, na prática, projetada segundo critérios de cálculo determinístico da temperatura máxima, conforme orientações regulamentares e técnicas da ABNT, através da NBR 5422.
Atenção
Em contrapartida, a consideração do uso de metodologias probabilísticas no cálculo da temperatura superficial, por exemplo, pode permitir aumentar a capacidade de transporte das linhas.
Adicionalmente ao conceito da temperatura superficial, é de fundamental importância compreender a relação de ampacidade, que corresponde:
"à corrente máxima que a linha de transmissão pode suportar para uma dada temperatura superficial do condutor, que está associada a uma distância mínima de segurança condutor-solo ou condutor-objeto"
MOREIRA, 2006, p. 47
Tais questões acerca dessas distâncias já foram amplamente discutidas no Tema 1 e, desta forma, abordaremos alguns detalhes principais desse ponto com relação à temperatura. Sabe-se ainda que, com a variação da temperatura do condutor, é evidente que devido às condições impostas ao material (por conta da dilatação) têm-se também variações na altura com relação ao solo. Para entender então possíveis relações de variação de temperatura, é fundamental compreender que a capacidade térmica de transmissão está limitada, na prática, à ocorrência de um dos dois fatores principais:
Rompimento da isolação devido à diminuição excessiva da altura com relação ao solo.
Dano ao cabo, devido ao recozimento em altas temperaturas.
Surgem, então, necessidades importantes e diversos estudos para avaliação da capacidade da linha, através da determinação da capacidade de transporte de energia, por exemplo, a ser calculada a qualquer momento tanto pela supervisão direta das temperaturas vistas nos cabos, quanto da formação da flecha ou da tração estabelecida.
A confiabilidade do sistema é analisada de forma completa desde o ponto de vista do projeto até a operação e o próprio planejamento, relacionada ao conhecimento desta capacidade de transporte em tempo real, previsões do valor máximo em horas e até dias dependendo da análise, da acurácia e de outras particularidades necessárias.
Para isto, na prática, estuda-se a ampacidade (de forma determinística ou estatística), faz-se o monitoramento em tempo real e são realizadas predições de carregamento, em grande parte dos casos.
Lembre-se que é fundamental o conhecimento das condições ambientais para tais importantes cálculos mecânicos citados, como evidencia a NBR 5422.
Recorre-se, então, a:
- temperatura média sem a presença do vento (com relação à condição de trabalho na maior parte do tempo neste sistema).
- a temperatura máxima média também sem vento.
- a temperatura mínima vista sem vento.
- a temperatura coincidente quando ocorre o vento na velocidade projetada.
O aumento da temperatura superficial do condutor leva ao rompimento da isolação e está relacionado diretamente aos limitantes da capacidade de transporte na linha aérea de transmissão.
A temperatura superficial máxima em condutores usuais com alma e de alumínio (tipo CAA), quando existem riscos térmicos já especificados, é estabelecida, em no máximo, 100°C por segurança. Para novos condutores, por outro lado, que possuam limites de temperaturas maiores que esses, a definição da temperatura máxima será dada pelos fabricantes geralmente (MOREIRA, 2006).
Perdas elétricas devido ao efeito joule
Para compreender as perdas elétricas devido ao efeito Joule, é possível analisar a linha de transmissão com relação a sua capacidade. Assim, tem-se como possibilidade o cálculo da potência característica e da potência natural ou SIL.
Potência característica
No cálculo da potência característica (P0 ou Pc), devem ser consideradas a tensão nominal de operação da linha (V) e a impedância característica (Z0), pois a potência é dada conforme a relação a seguir:
(61)
Para o cálculo da impedância característica, como já vimos ao longo desse tema, existem algumas considerações importantes necessárias. Além disso, ressalta-se que, para entender a operação da linha de transmissão, é possível considerar matematicamente que ela é modelada conforme um conjunto de equações gerais, baseando-se em teorias como o Modelo com Parâmetros Distribuídos (ZANETA JÚNIOR, 2006).
Assim, baseando-se no fato de que a linha de transmissão tenha comprimento infinito, sabe-se que a relação entre a tensão e a corrente em um ponto dela é independente do que estiver ligado em sua terminação.
Conforme as características resistivas e indutivas e considerando novamente o modelo teórico proposto, a impedância da linha por unidade de comprimento pode ser dada por:
Considerando que VC e IC representem a tensão e a corrente na carga, que Y’ é a admitância característica por metro e que γ é a constante de propagação, neste caso, dada por um número complexo em função da posição x ao longo da linha, a tensão nesta vale:
(62)
E a corrente (SARTORI, 2004):
(63)
Para x tendendo a infinito, o segundo termo da tensão e da corrente podem ser desprezados. Pela própria Lei de Ohm, adicionalmente, são possíveis simplificações e percebe-se que a impedância característica se torna independente da posição avaliada na linha:
(64)
Ou ainda:
(65)
Onde G’ é a condutância por unidade de comprimento e C’ a capacitância por unidade de comprimento, denominados juntamente com a resistência e a indutância da linha os parâmetros distribuídos desta.
Potência natural (SIL)
Por último, com relação à potência natural ou SIL, como também é conhecida, tem-se o valor da potência fornecida por uma linha, para uma carga resistiva pura que seja equivalente à impedância de surto desta linha.
Essa potência poderá ser utilizada para comparar as capacidades de carregamento das linhas de transmissão, por exemplo, e uma linha com carregamento abaixo da SIL gerará potência reativa. Caso seu valor esteja acima da SIL, isso implica o consumo de potência reativa (MOURA et al., 2019).
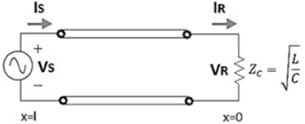
Caso a linha esteja carregada pela impedância de surto, tem-se o seguinte circuito equivalente simples, como apresentado na Figura 8, no qual o lado esquerdo correspondente ao emissor e o lado direito ao receptor:
A SIL vale em watts:
(66)
Exemplo
Há, no sistema elétrico brasileiro, tecnologias desenvolvidas para permitir o projeto de linhas de transmissão com potência natural elevada ou, ainda, para permitir a recapacitação de linhas que já estejam em operação. Nesse primeiro caso, visa-se essencialmente a realização de um projeto mais econômico.
Assim, perceba que a capacidade máxima da linha de transmissão pode ser avaliada pela potência natural e como evidenciado, esse critério vem servindo para o projeto de novas linhas de transmissão, em busca de maior eficiência e economia no processo além de monitoramento acerca de possíveis perdas.
Perdas elétricas devido ao efeito corona
Para o cálculo de perdas elétricas devido ao efeito corona (ou simplesmente perdas corona), considerando condições boas de tempo, é proposto por Peek o uso da equação seguinte na qual tem-se:
Por outro lado, tem-se mais adiante por Ryan e Henline, uma maneira de se calcular essas perdas de forma mais exata, próxima à região onde o corona ocorreu, no início:
(68)
Neste caso, C representa a capacitância fase-terra do condutor e f a frequência da tensão que é aplicada. Além dessa, há ainda, posteriormente, a seguinte fórmula, também considerando boas condições de tempo:
Para mais detalhes acerca do cálculo de F, sugere-se a leitura de Fuchs (1977).
Sob chuva, tem-se as condições estabelecidas por Gary e Cladé, como é visto na equação adiante:
[W/m](70)
Sendo que K é dado por:
(71)
Para a constante β de:
[cm](72)
Além disso, estima-se os seguintes valores para ρ:
para condutores simples e múltiplos, respectivamente
[cm](73)
R é dado por:
[cm](74)
No qual r é o raio dos n subcondutores usados, Rc o raio do condutor equivalente ao condutor múltiplo e Cs a capacitância de sequência positiva da linha trifásica.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Existem aspectos fundamentais que garantem o funcionamento da linha e do sistema de transmissão e, desta forma, do sistema elétrico também. Entre eles, é fundamental considerar certos parâmetros diretamente relacionados aos condutores, como os estabelecimentos dos campos elétricos e magnéticos, além de análises de efeitos aos quais as linhas estão frequentemente sujeitas, como o efeito corona e o próprio efeito Joule, capazes de proporcionar perdas elétricas significativas caso a linha não esteja projetada, operando e seu funcionamento planejado de formas adequadas.
Desta forma, no primeiro módulo, foram vistas as principais estratégias para estimar duas características importantes da linha: a indutância e a capacitância. Em seguida, viu-se acerca dos cálculos dos campos elétrico e magnético, adicionalmente, em um processo de análise de propagação de ondas e funcionamento do sistema, através da análise qualitativa. Já no segundo módulo, têm-se os principais aspectos sobre o efeito corona e a radiointerferência nas linhas de transmissão. Por último, no terceiro módulo, foram vistos parâmetros importantes como a temperatura superficial e a relação de ampacidade e foi feita uma análise quantitativa acerca das perdas elétricas devido ao efeito Joule e ao efeito corona.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Reconheceu as principais estratégias para os cálculos dos campos elétrico e magnético em cabos de linhas de transmissão
Identificou os efeitos relacionados à radiofrequência e ao efeito corona
Analisou os cálculos da temperatura superficial em cabos e das perdas devido aos efeitos Joule e corona