Descrição
Análise exploratória, medidas de posição e medidas de dispersão.
PROPÓSITO
Compreender as principais ferramentas de análise exploratória de dados e as medidas de posição e dispersão.
Preparação
Antes de iniciar o conteúdo deste tema, tenha em mãos uma calculadora científica ou use a calculadora de seu smartphone/computador.
OBJETIVOS
Módulo 1
Reconhecer as ferramentas de análise exploratória de dados
Módulo 2
Analisar as medidas de posição ou tendência central
Módulo 3
Descrever as medidas de dispersão ou variabilidade
Análise de Dados Quantitativos
MÓDULO 1
Reconhecer as ferramentas de análise exploratória de dados
Introdução
FERRAMENTAS DE ANÁLISE EXPLORATÓRIA DE DADOS
Iniciaremos agora o estudo de uma ferramenta importante da estatística e conheceremos os dados com os quais vamos trabalhar. Veremos neste módulo desde os conceitos básicos — tais como classificação de variáveis — até as principais ferramentas para apresentar e sintetizar os dados, como distribuição de frequência e representações gráficas.
Análise exploratória de dados
A análise exploratória de dados é a parte da estatística responsável pelo primeiro contato com as informações. Essa técnica nos dá um indicativo de como os dados estão distribuídos. Além disso, é útil na detecção de erros, de valores extremos (outliers), na verificação de suposições relacionadas à inferência estatística, na seleção preliminar de modelos estatísticos, entre outras utilidades. Aqui veremos os principais conceitos e ferramentas para a exploração correta dos dados.
Classificação das variáveis
Variáveis são características de interesse em um estudo qualquer. Elas podem ser classificadas em:
Quantitativas
Quando assumem valores numéricos.
Qualitativas
Quando seus possíveis valores não são numéricos.
A seguir veremos de forma resumida como as variáveis são classificadas:
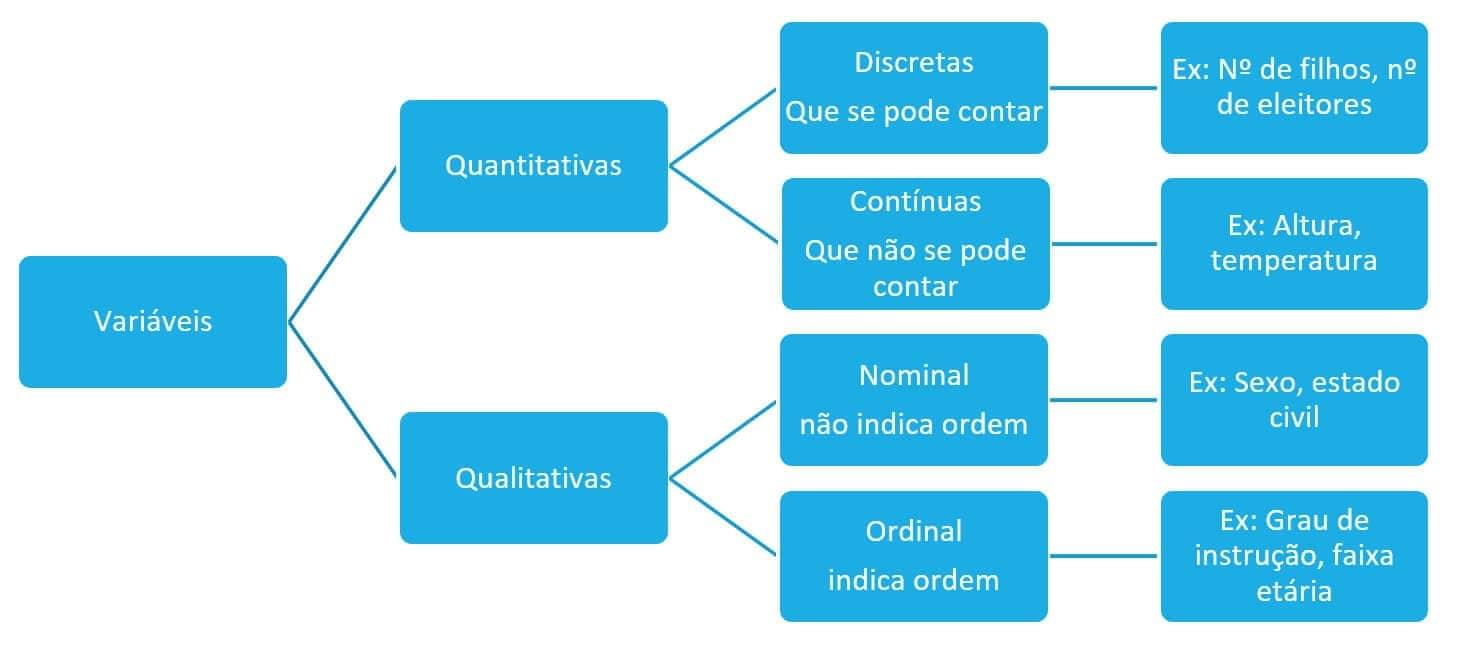
Conceitos básicos
Veremos, neste momento, uma série de conceitos que serão importantes, tanto para o melhor entendimento deste módulo como também para os seguintes.
População
Conjunto de indivíduos ou objetos com pelo menos uma característica em comum.
Amostra
É uma parte da população.
Dados brutos
Quando o conjunto de dados não tem uma ordem aparente chamamos de dados brutos.
Rol
Quando o conjunto de dados tem um ordenamento, seja crescente ou decrescente, dizemos que esses dados estão em rol.
Amplitude total
É a diferença entre o maior e o menor valor observado no conjunto de dados.
Distribuições de frequência
A distribuição de frequência é uma das formas mais simples e úteis de resumir um conjunto de dados.
Resumindo
Nada mais é do que a apresentação dos dados em classes às suas respectivas frequências absolutas.
As classes são divisões dos valores da variável em estudo.
Exemplo 1
A distribuição de frequência a seguir representa as notas na disciplina de estatística em uma turma de 40 alunos.
| Classe (Notas) | ||
|---|---|---|
| 1 | 2,5 | |
| 5 | 12,5 | |
| 12 | 30,0 | |
| 15 | 37,5 | |
| 7 | 17,5 | |
| Soma | 40 | 100 |
Exemplo 2
A próxima distribuição de frequência refere-se à quantidade de famílias que receberam auxílio escolar por número de filhos.
| Classe (Nº de filhos) | |
|---|---|
| 1 | 52 |
| 2 | 38 |
| 3 | 18 |
| 4 | 12 |
| Soma | 120 |
Elementos da distribuição de frequência
Há várias formas de expressar os limites de classe em uma distribuição de frequência. O limite à esquerda é chamado de limite inferior (Li) e o limite à direita é chamado de limite superior (Ls) da classe. Vejamos alguns exemplos:
- Li |---| Ls: indica uma classe que é fechada à esquerda e à direita, em que os limites inferior e superior estão incluídos na classe.
- Li |--- Ls: indica uma classe que é fechada à esquerda e aberta à direita, ou seja, o limite inferior está incluído na classe, mas o limite superior não.
- Li ---| Ls: indica uma classe que é fechada à direita e aberta à esquerda, ou seja, o limite superior está incluído na classe, mas o limite inferior não.
Dentre os limites de classes apresentados, o mais utilizado é o da letra B, isto é, fechada à esquerda e aberta à direita.
É a diferença entre o limite superior e o limite inferior da classe.
É a média aritmética entre o limite inferior e o limite superior da classe: 2 |---4. Logo o ponto médio dessa classe será:
OBS: No cálculo do ponto médio da classe (Xi), os limites superior e inferior são considerados, independentemente da classe ser fechada ou aberta nos limites Li ou Ls.
Relativa
A frequência relativa é dada por: , em que .
Exemplo:
| Classe (Notas) | ||
|---|---|---|
| 1 | 2,5 | |
| 5 | 12,5 | |
| 12 | 30,0 | |
| 15 | 37,5 | |
| 7 | 17,5 | |
| Soma | 40 | 100 |
Observe que para obter a frequência relativa de cada classe, basta dividir a frequência absoluta de cada uma por n, que é o tamanho do conjunto de dados ou tamanho da amostra. Então, , , , e assim por diante. Veja que o processo é análogo para todas as classes.
É o acúmulo das frequências absolutas. A partir da primeira frequência, somam-se as respectivas frequências absolutas.
Exemplo:
| Classe (Notas) | ||
|---|---|---|
| 1 | 1 | |
| 5 | 6 | |
| 12 | 18 | |
| 15 | 33 | |
| 7 | 40 | |
| Soma | 40 | - |
Veja que, para a primeira classe, a frequência acumulada é igual à frequência absoluta. A partir daí, começamos a somar as frequências absolutas, de forma que a acumulada da segunda classe é a frequência absoluta da primeira classe mais a frequência absoluta da segunda classe, ou seja, . Para determinar a frequência acumulada da terceira classe, somamos a frequência acumulada da segunda com a frequência absoluta da terceira, ou seja, , e assim por diante.
Como construir uma distribuição de frequência
Muitas vezes, a distribuição dos dados é obtida de forma que estão simplesmente dispostos em rol ou mesmo como dados brutos, ou seja, sem ordem aparente.
Dica
Quando a quantidade de dados é muito grande, a melhor forma de apresentá-los é por meio de uma tabela.
No intuito de melhorar a apresentação, é comum dispor os dados em uma distribuição de frequência. Desse modo, veremos a seguir alguns passos práticos para construir uma distribuição de frequência.
Passo 1: Determinar o número de classes (k).
Para se calcular o número de classes de uma distribuição de frequência, utilizaremos a seguinte fórmula:
Na qual n é o tamanho do conjunto de dados ou da amostra.
Passo 2: Determinar a Amplitude Total (AT).
A amplitude de classe é a diferença entre o maior e o menor valor no conjunto de dados.
Passo 3: Determinar a Amplitude de Classe (Ac).
A amplitude de classe é obtida por:
Passo 4: Construção da distribuição de frequência.
A partir dos três elementos vistos nos passos 1, 2 e 3 iniciaremos a construção da distribuição de frequência pelo menor valor do conjunto de dados, que será o limite inferior da primeira classe.
A partir desse valor, acrescentamos a amplitude de classe para obter o limite superior da primeira classe. Esse limite superior da primeira classe será o limite inferior da segunda, independentemente do tipo de classe escolhida. O limite superior da segunda classe será o limite inferior da segunda somada à amplitude de classe.
Atenção
O limite superior da segunda classe será o limite inferior da terceira e assim por diante. É comum na última classe usarmos a classe fechada tanto no limite inferior como no limite superior.
Exemplo
O rol a seguir representa a altura (em centímetros) de 26 jogadores de uma equipe de futebol.
160 165 166 168 170 170 172 174 175 175 175 178 180 180 182 183 185 185 187 188 188 190 191 195 198 200
Construa uma distribuição de frequência das alturas dos jogadores dessa equipe de futebol.
Passo 1:
Nesse caso, usaremos a regra de arredondamento e consideraremos k igual a 5, mas em alguns casos é interessante arredondar para cima, sempre verificando se a distribuição de frequência contempla todo o conjunto de dados.
Passo 2:
Passo 3:
Passo 4:
Construindo a distribuição de frequência.
| Classe (Alturas) | |
|---|---|
| 3 | |
| 8 | |
| 5 | |
| 7 | |
| 3 | |
| Soma | 26 |
Representações gráficas
A seguir, veremos alguns meios de sintetizar os dados de uma forma gráfica.
Atenção
Embora atualmente não seja mais necessário saber as técnicas de construção dos gráficos como se fazia há alguns anos, é importante conhecer os principais tipos de gráficos e quando devem ser empregados, pois ainda hoje são ferramentas indispensáveis para visualização e interpretação de dados.
É o tipo de gráfico mais utilizado em geral, pois serve para representar quaisquer dados quantitativos.
Exemplo: Considere a distribuição de frequência referente à quantidade de famílias que receberam auxílio escolar por número de filhos.
| Classe (Nº de filhos) | |
|---|---|
| 1 | 52 |
| 2 | 38 |
| 3 | 18 |
| 4 | 12 |
| Soma | 120 |
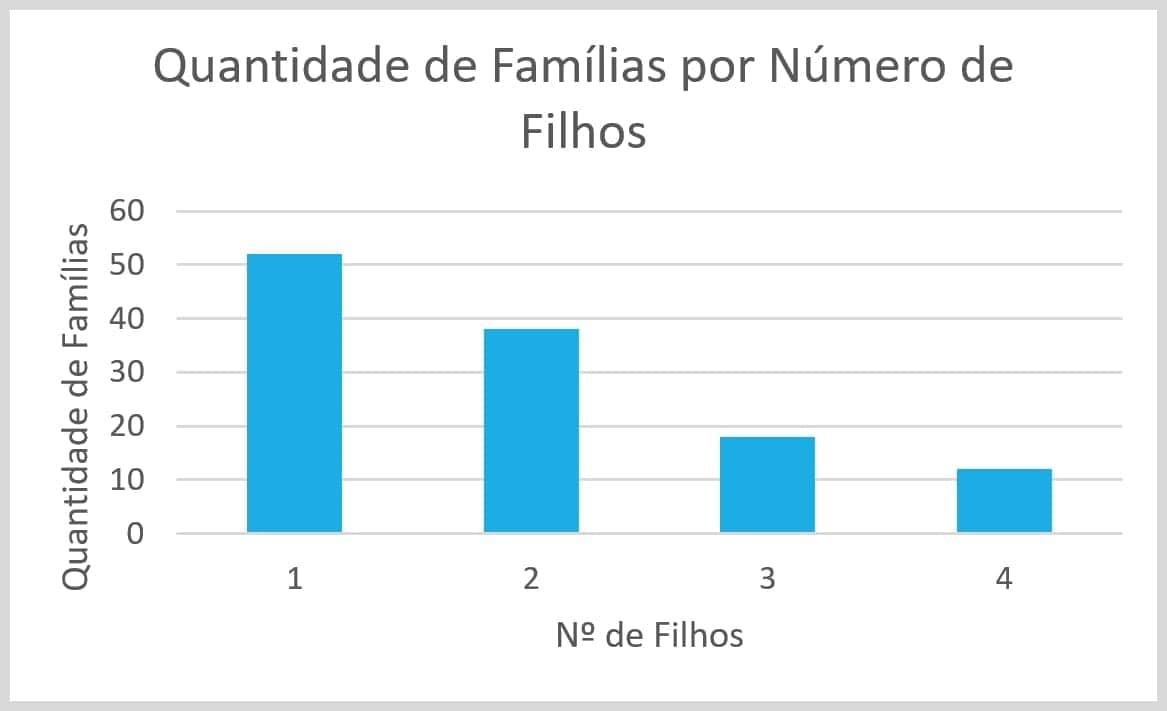
Esse é o gráfico típico da distribuição de frequência. A diferença desse gráfico para o gráfico de barras ou colunas se dá pelo fato de as colunas apresentarem-se justapostas, ou seja, sem espaçamento entre elas. Em geral, a abcissa desse gráfico é representada pelas classes e a ordem é representada pela frequência absoluta ou relativa.
Exemplo: Considere a distribuição de frequência a seguir, que representa as notas na disciplina de estatística em uma turma de 40 alunos.
| Classe (Notas) | ||
|---|---|---|
| 1 | 2,5 | |
| 5 | 12,5 | |
| 12 | 30,0 | |
| 15 | 37,5 | |
| 7 | 17,5 | |
| Soma | 40 | 100 |
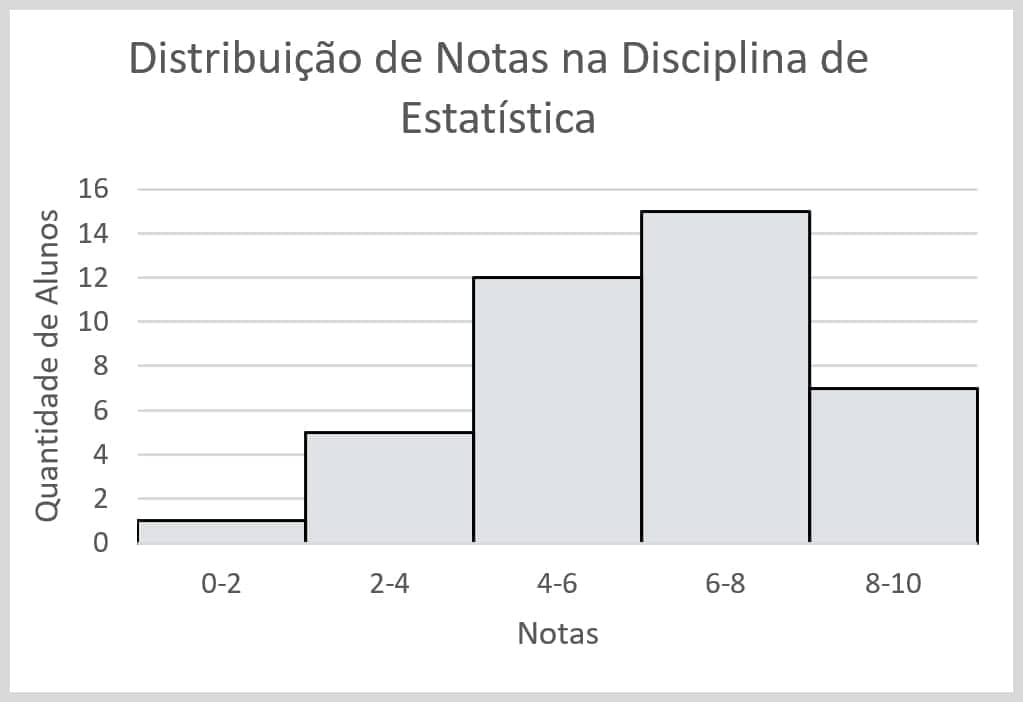
É o gráfico mais apropriado quando trabalhamos com uma série de tempo.
Exemplo: Número de acidentes por mês ao longo de um ano.
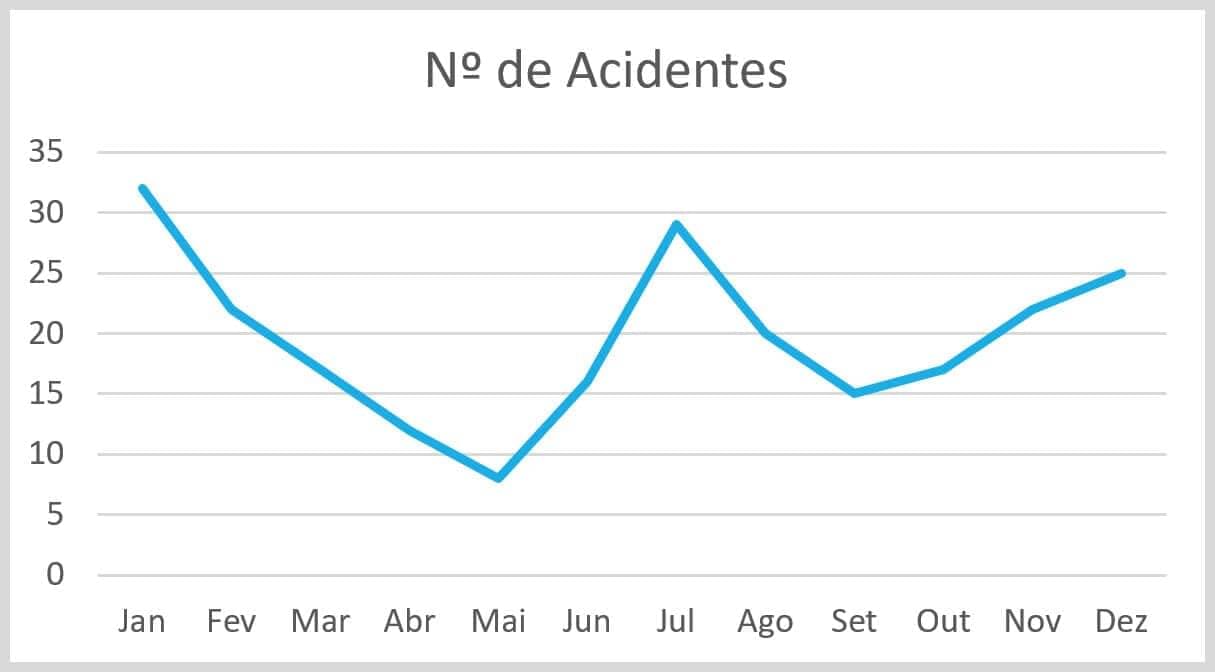
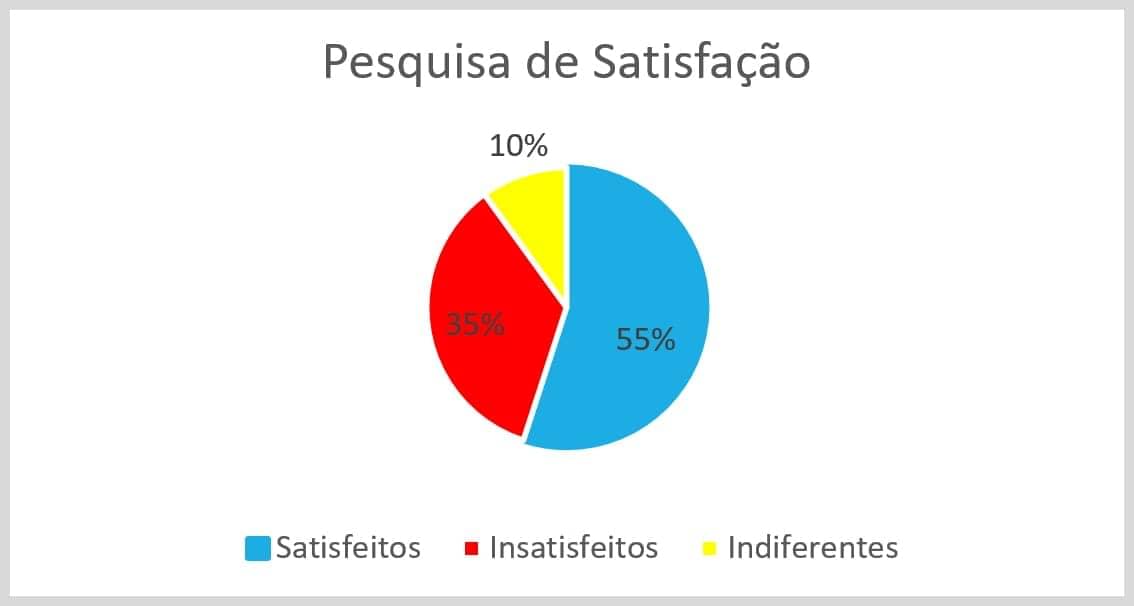
É o gráfico mais apropriado quando trabalhamos com porcentagens.
Exemplo: Em uma pesquisa de satisfação sobre determinado produto, 55% dos entrevistados disseram que estavam satisfeitos, 35% disseram que estavam insatisfeitos e 10% disseram que eram indiferentes.
É um dos gráficos mais utilizados atualmente, visto que traz várias informações sobre o conjunto de dados. Com esse gráfico é possível verificar a tendência central, a variabilidade e a simetria da distribuição dos dados, conceitos esses que serão vistos de forma mais detalhada posteriormente no Módulo 2.
Outra vantagem desse gráfico é que podemos observar a presença de valores atípicos (outliers). Para isso é necessário determinar o intervalo interquartil (IQR), que é a diferença entre o 3º e o 1º quartil. Multiplicando esse IQR por 1,5, obtemos a faixa interquartil. Quando subtraímos o 1º quartil dessa faixa e somamos o 3º quartil a esta, encontramos o intervalo no qual seria comum a variação dos dados. Valores acima desse intervalo são considerados outliers.
Exemplo: Considere os dados referentes aos preços de aluguéis de imóveis (em reais) em certo bairro do Rio de Janeiro.
1000 1500 1800 2000 2200 2500 2600 3000 3500 7000
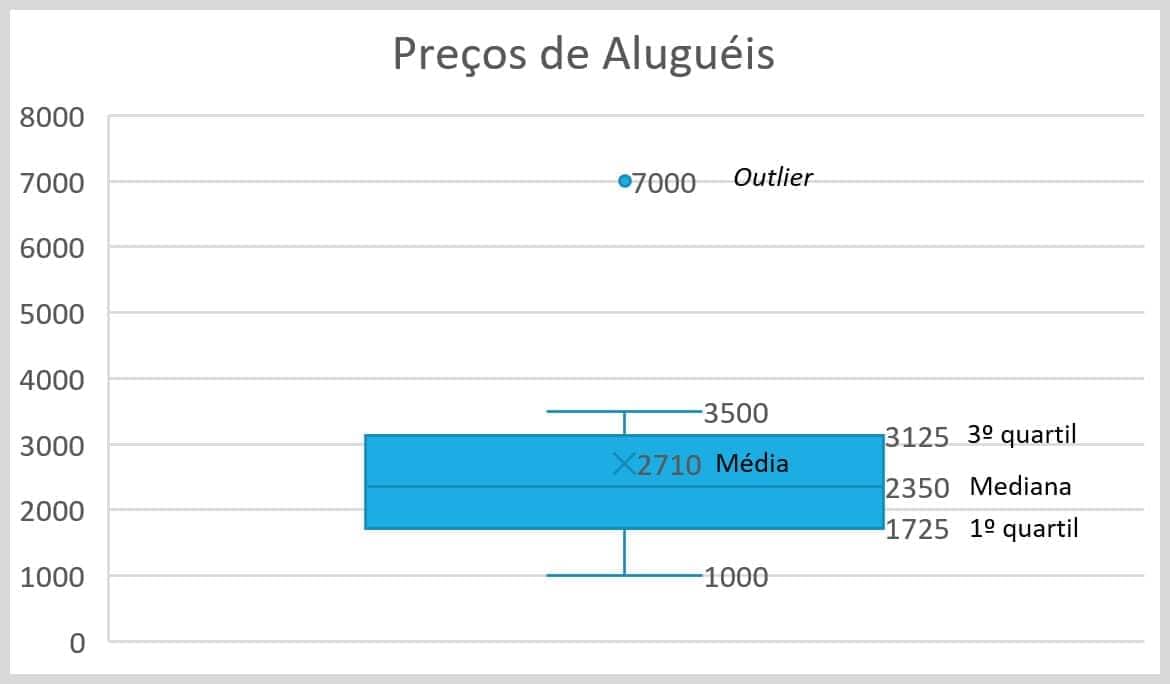
Observe que nesse gráfico temos informações como: o primeiro e o terceiro quartis, a mediana e a média. Os traços abaixo do primeiro quartil e acima do terceiro quartil representam o menor e o maior valor dentro do intervalo normal de variação dos dados.
Como vimos, o IQR é calculado subtraindo o terceiro quartil do primeiro quartil, que, nesse caso, é igual a 1400. Note que a faixa interquartil (1,5IQR) é igual a 2100; logo, se somarmos o 3º quartil a essa faixa interquartil, temos o valor limite (5225), que seria considerado normal para variação dos aluguéis. No entanto, como o aluguel de R$7.000,00 reais está acima de R$5.225,00 podemos dizer que se trata de um valor atípico.
Mão na Massa

Teoria na prática
O conjunto de dados a seguir representa o número de horas extras mensais trabalhadas por 17 funcionários de um banco de investimentos:
10 12 12 14 15 16 16 18 19 20 20 21 24 24 25 28 30
Organize os dados em uma distribuição de frequência.
DISTRIBUIÇÃO DE FREQUÊNCIA
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Analisar as medidas de posição ou tendência central
Introdução
MEDIDAS DE POSIÇÃO OU TENDÊNCIA CENTRAL
Medidas de Posição ou Tendência Central
Medidas de posição ou tendência central são medidas que visam representar os fenômenos por seus valores centrais, em torno dos quais tendem a concentrar-se os dados. Apresentaremos essas medidas de acordo com os conceitos vistos no módulo anterior, ou seja, considerando que os dados podem apresentar-se:
Agrupados
Quando estão dispostos em uma distribuição de frequência.
Não agrupados
Quando estão dispostos em rol ou dados brutos.
Veja a seguir as principais medidas de posição:
Média
É a medida de posição mais conhecida e mais usada na prática para verificar o comportamento central dos dados. Vejamos a definição da média considerando a forma como os dados são apresentados:
Para dados não agrupados
Quando os dados estão dispostos como dados brutos ou rol, a média é definida por:
Exemplo 1
Determine a média para o seguinte Rol de dados: 1, 2, 3, 4, 5.
Logo, a média é igual a 3.
Para dados agrupados
Quando os dados se apresentam em distribuição de frequência, a média é definida por:
Em que:
é ponto médio da classe i
é a frequência absoluta da classe i
n é tamanho do conjunto de dados ou da amostra
Exemplo 2
Considere os dados sobre o peso (em Kg) de recém-nascidos de certa maternidade, dispostos na distribuição de frequência abaixo:
| Classe | |
|---|---|
| 2 | |
| 4 | |
| 7 | |
| 5 | |
| 5 | |
| 7 | |
| Soma | 30 |
Vimos que, para calcular a média para dados agrupados, usamos a seguinte expressão:
Dessa forma, precisamos determinar o produto de . Assim, podemos utilizar a própria distribuição de frequência acima para obter esse produto. Daí,
| Classe | |||
|---|---|---|---|
| 2 | 2,25 | 4,5 | |
| 4 | 2,75 | 11 | |
| 7 | 3,25 | 22,75 | |
| 5 | 3,75 | 18,75 | |
| 5 | 4,25 | 21,25 | |
| 7 | 4,75 | 33,25 | |
| Soma | 30 | - | 111,5 |
Portanto, a média é calculada da seguinte forma:
Logo, a média do peso dos recém-nascidos dessa maternidade é de aproximadamente 3,72 kg.
Mediana
Disposto o conjunto de dados em ordem crescente ou decrescente, a mediana é o elemento que ocupa a posição central, isto é, divide o conjunto de dados em duas partes iguais, de forma que metade dos dados está acima e a outra metade está abaixo da mediana.
Para dados não agrupados
Para o cálculo da mediana para dados não agrupados, serão levados em consideração dois fatores:
Se o tamanho da amostra é ímpar ou par
Se refere ao elemento mediano, que é o elemento que nos dá a posição ocupada pela mediana.
A mediana será o valor dado pela posição determinada pelo elemento mediano.
Exemplo: Considere o seguinte conjunto de dados: 2, 5, 7, 9, 10. Assim, como n = 5, temos:
Veja que o elemento que ocupa a terceira posição no conjunto de dados é justamente o número 7. Portanto, a mediana é igual a 7.
A mediana será a média aritmética entre as medianas obtidas pela posição dos elementos medianos e , que são determinados da seguinte forma:
Exemplo: 3, 4, 6, 8, 10, 11
Observe que, nesse caso, o primeiro elemento mediano é o elemento que ocupa a terceira posição e o segundo elemento mediano é o elemento que ocupa a quarta posição, o que equivale aos valores 6 e 8, respectivamente. Então, a mediana é a média aritmética entre esses valores (6 e 8), que é igual a 7.
Para dados agrupados
Para o cálculo da mediana para dados agrupados, vamos seguir os seguintes passos:
Determinar o elemento mediano.
Determinar a classe mediana , que é a classe que contém o elemento mediano.
Aplicar a fórmula:
Em que:
Limite inferior da classe mediana.
Frequência acumulada anterior à classe mediana.
Frequência absoluta da classe mediana.
Amplitude da classe mediana (diferença entre as amplitudes de classe superior e inferior).
Exemplo
Considerando os dados dos pesos dos recém-nascidos, determine o valor da mediana.
| Classe | |
|---|---|
| 2 | |
| 4 | |
| 7 | |
| 5 | |
| 5 | |
| 7 | |
| Soma | 30 |
Vimos que para calcular a mediana é necessário obter a classe mediana. Dessa forma, para determinar quem é a classe mediana é necessário obter a frequência acumulada (Fac) para cada classe.
Relembrando
Para determinar as frequências acumuladas de cada classe, basta ir acumulando (somando) as frequências absolutas.
| Classe | ||
|---|---|---|
| 2 | 2 | |
| 4 | 6 | |
| 7 | 13 | |
| 5 | 18 | |
| 5 | 23 | |
| 7 | 30 | |
| Soma | 30 | - |
Seguindo os passos para o cálculo da mediana para dados agrupados, temos:
1) Determinar o elemento mediano.
Note que esse elemento mediano ocupa a décima quinta posição no conjunto de dados.
2) Determinar a classe mediana , que é a classe que contém o .
A classe que contém o elemento mediano é a quarta classe, visto que ela contém o décimo quinto elemento. Note ainda, que essa classe contém do décimo quarto ao décimo oitavo elemento.
| Classe | |||
|---|---|---|---|
| 2 | 2 | ||
| 4 | 6 | ||
| 7 | 13 | ||
| 5 | 18 |
→ Classe Mediana |
|
| 5 | 23 | ||
| 7 | 30 | ||
| Soma | 30 | - | |
|
|
|||
3) Aplicando a fórmula, temos:
Por isso, a mediana do peso dos recém-nascidos é igual a 3,7 Kg.
A interpretação da frequência acumulada é feita da seguinte forma: note que na primeira classe, temos o primeiro e o segundo elementos do conjunto de dados, pois os dados estão em ordem crescente, conforme definição de mediana.
Na segunda classe, temos do terceiro ao sexto elemento. Na terceira classe, temos do sétimo ao décimo terceiro elemento, e assim por diante, de forma que, a última classe contém do vigésimo quarto ao trigésimo elemento.
Atenção
Verifique que o valor da frequência acumulada da última classe deve ser igual à soma da frequência absoluta.
Moda
É o valor mais frequente no conjunto de dados.
Para dados não agrupados
Para determinar a moda nesse caso, basta ver o valor que mais se repete no conjunto de dados.
Dica
Caso nenhum valor se repita, dizemos que o conjunto de dados é amodal.
Exemplo 1:
, veja que o número 2 é o valor que mais se repete.
Exemplo 2:
, pois não temos nenhuma repetição dos valores.
Exemplo 3:
(bimodal)
Para dados agrupados
Nesse caso, para obter a moda, seguiremos os seguintes passos:
Determinar a classe modal , que é a classe com maior frequência, seja ela absoluta ou relativa.
Calcular a moda a partir da fórmula de Czuber:
Em que:
Limite inferior da classe modal.
Frequência absoluta da classe modal – Frequência absoluta da classe imediatamente anterior.
Frequência absoluta da classe modal – Frequência absoluta da classe imediatamente posterior.
Atenção
Observe que os valores obtidos para as modas são apenas aproximações. Eles devem ser obtidos desse modo somente se não for possível dispor dos dados originais.
Exemplo
Considerando novamente os dados dos pesos dos recém-nascidos, obtenha o valor da moda.
| Classe | |
|---|---|
| 2 | |
| 4 | |
| 7 | |
| 5 | |
| 5 | |
| 7 | |
| Soma | 30 |
Seguindo os passos para a determinação da moda para o caso de dados agrupados, temos:
1) Determinar a classe modal que, como vimos, é a classe com maior frequência absoluta.
| Classe | |
|---|---|
| 2 | |
| 4 | |
| 7 | |
| 5 | |
| 5 | |
| 7 | |
| Soma | 30 |
Veja que, nesse caso, temos duas classes com maiores frequências absolutas. Por isso, teremos duas classes modais e, assim, duas modas associadas a esse conjunto de dados.
2) Calculando as modas:
Na qual
Na qual
Note que há um caso especial, pois a segunda classe modal está na última classe e, para o cálculo de , considera-se que a classe imediatamente posterior é igual a zero. O mesmo procedimento deve ser adotado quando a classe modal está na primeira classe, com a diferença que, nesse caso, para o cálculo de considera-se que a classe imediatamente anterior é igual a zero.
Separatrizes
As separatrizes têm a função de dividir o conjunto de dados em certo número de partes iguais. A mediana que divide os dados em duas partes iguais é um caso particular de separatriz. No entanto, outras separatrizes têm papel de destaque na estatística, como é o caso dos quartis, decis e percentis, cujos conceitos serão vistos a seguir.
Quartil
O quartil divide o conjunto de dados em quatro partes iguais.

Q1 = 1º quartil, representa 25% dos elementos.
Q2 = 2º quartil, coincide com a mediana, representa 50% dos elementos.
Q3 = 3º quartil, representa 75% dos elementos.
Q4 = 4º quartil, representa 100% dos elementos
Para o cálculo dessas medidas, serão adotados os mesmos procedimentos realizados para o cálculo da mediana para dados agrupados. Assim, seguiremos os passos a seguir.
Determinar o elemento quartil.
Lembre-se de que, neste caso, há quatro quartis, ou seja, i = 1, 2,3,4. Observe que se i = 2, equivale à mediana. Além disso, não importa se n é ímpar ou par, pois estamos trabalhando com dados agrupados.
Determinar a classe quartil i , que é a classe que contém o elemento quartil i.
Aplicar a fórmula:
Em que:
Limite inferior da classe quartil i.
Frequência acumulada anterior à classe quartil i.
Frequência absoluta da classe quartil i.
Amplitude da classe quartil i (diferença entre as amplitudes de classe superior e inferior).
Exemplo
A corretora XYZ tem em seu portifólio 60 imóveis que foram distribuídos de acordo com seu valor de venda (em milhares de reais). Os dados estão representados na distribuição de frequência a seguir:
| Classe | ||
|---|---|---|
| 5 | 5 | |
| 17 | 22 | |
| 20 | 42 | |
| 13 | 55 | |
| 5 | 60 | |
| Soma | 60 | - |
A partir de que valor estão os 25% dos imóveis mais caros dessa corretora?
Solução: Note que o problema pede para determinar o valor que divide os 25% mais caros dos 75% mais baratos, o que é equivalente a determinar o 3º quartil (Q3). Então:
1) Determinar o elemento quartil 3.
Determinar a classe quartil 3 .
| Classe | ||
|---|---|---|
| 5 | 5 | |
| 17 | 22 | |
| 20 | 42 | |
| 13 | 55 | |
| 5 | 60 | |
| Soma | 60 | - |
Observe pela frequência acumulada que a classe que contém o elemento quartil 3 é a quarta, visto que essa classe contém do elemento ao .
3) Aplicando a fórmula, temos:
Portanto, o valor pedido é de R$346.150,00 reais.
Decil
O Decil divide o conjunto de dados em 10 partes iguais.

O cálculo dos decis é análogo ao dos quartis. Dessa forma, os seguintes passos serão realizados:
Determinar o elemento decil i.
Aqui temos 10 decis, ou seja, i = 1, 2,3, ... ,10. Observe que se i = 5, equivale à mediana e ao segundo quartil.
Determinar a classe decil i , que é a classe que contém o elemento decil i.
Aplicar a fórmula:
Na qual:
Limite inferior da classe decil i.
Frequência acumulada anterior à classe decil i.
Frequência absoluta da classe decil i.
Amplitude da classe decil i (diferença entre as amplitudes de classe superior e inferior).
Exemplo
Considerando o exemplo da corretora, a partir de que valor estão os 10% dos imóveis mais baratos?
Solução: Veja que o problema pede para determinar o valor que representa justamente o 10º decil. Logo:
1) Determinar o elemento decil 1.
2) Determinar a classe decil 1 .
Veja que a classe que contém o elemento decil 1 é a segunda classe.
| Classe | ||
|---|---|---|
| 5 | 5 | |
| 17 | 22 | |
| 20 | 42 | |
| 13 | 55 | |
| 5 | 60 | |
| Soma | 60 | - |
3) Aplicar a fórmula:
Logo, o valor pedido é R$135.300,00 reais.
Percentil
O percentil divide o conjunto de dados em 100 partes iguais.

Determinar o elemento percentil i.
Neste caso, temos 100 percentis, ou seja, i = 1, 2,3, ... ,100. Observe que se i = 50, equivale à mediana, ao segundo quartil e ao quinto decil.
Determinar a classe decil i , que é a classe que contém o elemento decil i.
Aplicar a fórmula:
Na qual:
Limite inferior da classe percentil i.
Frequência acumulada anterior à classe percentil i.
Frequência absoluta da classe percentil i.
Amplitude da classe percentil i (diferença entre as amplitudes de classe superior e inferior).
Exemplo
Considerando o exemplo da corretora, a partir de que valor estão 1% dos imóveis mais caros?
Solução: Veja que o problema pede para determinar o valor que representa justamente o 99º percentil. Então:
1) Determinar o elemento percentil 99.
2) Determinar a classe percentil 99 .
Veja que classe que contém o elemento percentil 99 é a quinta classe.
| Classe | ||
|---|---|---|
| 5 | 5 | |
| 17 | 22 | |
| 20 | 42 | |
| 13 | 55 | |
| 5 | 60 | |
| Soma | 60 | - |
3) Aplicando a fórmula, temos:
Logo, o valor pedido é R$764.000,00 reais.
Mão na Massa

Teoria na prática
Uma loja de produtos naturais tem suas vendas (em reais) do mês de janeiro apresentadas na distribuição de frequência a seguir:
| Venda (R$) | |
|---|---|
| 24 | |
| 52 | |
| 80 | |
| 38 | |
| 6 | |
| Soma | 200 |
Qual a média de vendas da loja no mês de janeiro?
CÁLCULO DE MÉDIA
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Descrever as medidas de dispersão ou variabilidade
Introdução
MEDIDAS DE DISPERSÃO OU VARIABILIDADE
A seguir veremos as medidas de dispersão ou variabilidade, as quais possuem grande utilidade, pois avaliam o grau de dispersão dos dados em torno da média. Elas servem para verificar a representatividade da média. Vamos analisar os conceitos das principais medidas de dispersão, tais como variância, desvio-padrão e coeficiente de variação.
Variância
A variância e o chamado desvio-padrão são as medidas mais conhecidas, servindo de base para medir o quanto os dados estão dispersos com relação à média, ou seja, o quanto os dados estão afastados da média.
Uma forma de calcular o afastamento de cada dado da média é calcular a diferença entre o dado e a média. Mas se calcularmos todas estas diferenças e as somarmos, obteremos ZERO. Ou seja, tal soma não avalia o afastamento total...
Veja:
Então, uma forma de evitar que o cálculo do desvio TOTAL simplesmente nos conduza ao valor zero é, por exemplo, elevar ao quadrado os desvios anteriores, ANTES de somá-los!
De fato, chamamos de desvio quadrático total (DQ), ao somatório dos desvios subtrativos simples, previamente elevados ao quadrado, ou seja:
Para calcularmos um desvio quadrático médio que é a medida de dispersão de nosso interesse, chamada de VARIÂNCIA, devemos analisar duas situações:
- Dispomos de todos os dados que temos interesse em analisar, ou seja, toda a POPULAÇÃO;
- Os dados fornecidos correspondem apenas a uma AMOSTRA dos dados totais de interesse.
Além disso, é útil distinguir as situações em que os dados estão agrupados ou não.
O estudo mais avançado da estatística nos indica que o desvio quadrático médio da população e de uma amostra devem ser calculados como se segue:
População Variância:
Amostra Variância:
Observe que no caso da população, dividimos o desvio quadrático total pela própria quantidade n de objetos da população em análise.
Entretanto, no caso de analisarmos uma amostra, devemos realizar um ajuste, justificado pela estatística, e que envolve o conceito de graus de liberdade, que não é abordado neste nível de curso.
Devemos, então, neste caso, dividir o desvio quadrático total por n-1, e não por n, a quantidade de elementos da nossa amostra.
Observação
Se tivermos os dados agrupados em uma tabela de frequência, podemos escrever:
População Variância:
Amostra Variância:
Onde é a média do conjunto de dados e a frequência das amostras.
Exemplo
Considere a seguinte amostra de dados: 1, 3, 5, 7 e 9. Determine o valor da variância.
Solução: Veja que, para determinar a variância, é necessário inicialmente calcular a média dos dados.
Dados agrupados
O cálculo da variância para dados agrupados, ou seja, quando os dados estão dispostos em distribuição de frequência, levam em consideração o ponto médio da classe e a frequência absoluta. Tecnicamente, supõe-se que o ponto médio de cada classe é um bom representante dos dados de cada classe.
Desse modo, temos:
População Variância:
Amostra Variância:
onde xi é o ponto central da i=ésima classe e f¬i a frequência absoluta da i-ésima.
Exemplo
Considere os dados sobre o peso (em Kg) de uma amostra de recém-nascidos de certa maternidade dispostos na distribuição de frequência abaixo:
| Classe | |
|---|---|
| 2 | |
| 4 | |
| 7 | |
| 5 | |
| 5 | |
| 7 | |
| Soma | 30 |
Solução: Veja que, para calcularmos a variância, vamos precisar dos produtos e . Assim, podemos utilizar a própria distribuição de frequência anterior para obter esses produtos. Daí:
| Classe | ||||
|---|---|---|---|---|
| 2 | 2,25 | 4,5 | 10,125 | |
| 4 | 2,75 | 11 | 30,25 | |
| 7 | 3,25 | 22,75 | 73,9375 | |
| 5 | 3,75 | 18,75 | 70,3125 | |
| 5 | 4,25 | 21,25 | 90,3125 | |
| 7 | 4,75 | 33,25 | 157,9375 | |
| Soma | 30 | - | 111,5 | 432,875 |
Logo,
Note que essa medida tem a interpretação prejudicada, visto que eleva ao quadrado os desvios . Esse fato faz com que a unidade da variável com que estamos trabalhando fique ao quadrado.
Observação
Se a variável de interesse é medida em quilogramas (Kg), como no exemplo acima, a variância nos dará a resposta em quilogramas ao quadrado (Kg2) e isso compromete a interpretação da referida medida. Para solucionar esse problema, foi criado o desvio-padrão, que será a próxima medida que veremos.
Desvio-padrão (S)
O desvio-padrão é simplesmente definido como a raiz quadrada da variância, pois sua unidade, então, é exatamente a unidade dos dados! Assim, fica claro porque indicamos a variância por S2. Ou seja, S é o desvio-padrão da população ou da amostra.
Exemplo: Considerando o exemplo da variância para dados não agrupados, temos:
Vimos que nesse exemplo o resultado da variância foi igual a 10. Logo,
Relembrando
O desvio-padrão é uma medida de variabilidade dos dados em torno da média.
Então nesse caso, podemos dizer que a dispersão em torno da média é de 3,2. Portanto, com essa medida, é possível verificar como se concentram os dados em torno da média.
Dados agrupados
Exemplo: Considerando os dados sobre o peso (em Kg) de recém-nascidos, temos:
Interpretação: A variabilidade em torno da média de 1 kg.
Note que, apesar de o desvio-padrão ser uma boa medida da variabilidade, é uma medida absoluta, e nem sempre conseguimos ver com clareza se o seu valor reflete maior ou menor variabilidade dos dados.
Exemplo
Imagine um analista que trabalha com uma quantidade enorme de dados, por exemplo, na casa dos milhares ou mesmo milhões de dados: seria quase impossível dizer se a dispersão desses dados é alta ou baixa, simplesmente observando o valor do desvio-padrão. Para resolver tal problema, foi criado o coeficiente de variação, que veremos a seguir.
Coeficiente de variação (CV%)
O coeficiente de variação é uma medida de dispersão relativa, sendo muito útil quando temos uma quantidade expressiva de dados ou quando queremos fazer comparações entre variáveis que são medidas em diferentes amostras ou populações. Essa medida é definida por:
Em que:
é o desvio-padrão
a média da amostra
Na prática, considera-se a seguinte regra para dizer se os dados são poucos ou muito dispersos:
Pouca dispersão
Dispersão moderada
Alta dispersão
Exemplo
Foi aplicada uma prova de conhecimentos gerais em duas turmas, digamos A e B. A turma A obteve média 8 e desvio-padrão 2, a turma B obteve média 6,5 e desvio-padrão 1,8. Qual turma teve maior dispersão em torno da média?
Solução: Aparentemente, a turma que teve maior dispersão foi a A, pois tem desvio-padrão igual a 2, enquanto a turma B teve desvio-padrão igual a 1,8. Porém, para sabermos de fato qual turma teve maior variabilidade, temos que calcular o coeficiente de variação. Assim:
e
Portanto, a turma B teve maior dispersão do que a turma A. Note que ambas as turmas apresentam dispersão moderada.
Mão na Massa

Teoria na prática
Considere que os dados informados a seguir se referem à idade dos alunos de duas turmas de inglês.
Turma 1: 8, 8, 8, 9, 9, 10, 10, 12
Turma 2: 17, 17, 19, 19, 20, 20, 21, 23
Em qual das duas turmas as idades dos alunos é mais espalhada?
CÁLCULO DA MÉDIA
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Divididos em três módulos, abordamos conceitos fundamentais de análise de dados quantitativos. No primeiro módulo vimos conceitos associados a análise exploratória de dados, que tem por objetivo oferecer um panorama inicial sobre o conjunto de dados. Além disso, aprendemos formas de organizá-los e representá-los graficamente. No segundo e no terceiro módulo, respectivamente, trabalhamos as principais medidas de tendência central e variabilidade, medidas essas com vastas aplicações práticas no dia a dia.
Todos os conceitos adquiridos sobre esse tema contêm grande aplicabilidade e servem para dar continuidade ao seu aprendizado de estatística.
CONQUISTAS
Você atingiu os seguintes objetivos:
Reconheceu as ferramentas de análise exploratória de dados
Analisou as medidas de posição ou tendência central
Descreveu as medidas de dispersão ou variabilidade
