Descrição
Utilização da amostragem estratificada para estimação das quantidades de interesse, Alocação das amostras entre os estratos, Estimação da proporção e o tamanho amostral necessário para esses cálculos.
PROPÓSITO
Apresentar a técnica de amostragem estratificada para estimação das quantidades de interesse em uma pesquisa, realizando a alocação da amostra para distribuir essas unidades nos estratos.
Preparação
Antes de iniciar o conteúdo deste tema, certifique-se de ter papel e lápis por perto para acompanhar os exemplos e demonstrações. Além disso, a tabela da distribuição normal será importante quando estudarmos os tamanhos amostrais.
OBJETIVOS
Módulo 1
Descrever o método de seleção por amostragem aleatória estratificada, a importância da utilização de estratos e as razões para estratificação
Módulo 2
Definir as notações utilizadas na estratificação, com as expressões de estimação de totais, médias e variâncias na amostragem estratificada
Módulo 3
Definir variáveis de proporção e o tamanho de amostra utilizado na amostragem estratificada simples com as diferentes alocações disponíveis
Introdução
Abordaremos inicialmente os conceitos básicos da amostragem estratificada e os aspectos sobre sua seleção. Em seguida, faremos estimações de algumas variáveis de interesse, como a média e o total, por exemplo. Além disso, aprenderemos as diferentes formas de alocação das amostras nos estratos. Conheceremos também a estimação para variáveis do tipo proporção e, por fim, veremos como calcular o tamanho de amostra para as diferentes alocações amostrais.
MÓDULO 1
Descrever o método de seleção por amostragem aleatória estratificada, a importância da utilização de estratos e as razões para estratificação
Introdução
Em muitas pesquisas, há um interesse em se criar estratos de seleção, o que chamamos de estratificação. Depois de criados esses estratos, podemos selecionar amostras de cada um desses grupos, o que irá constituir nossa amostragem estratificada.

Este módulo analisará os tipos de seleção por amostragem aleatória estratificada. Veremos quais as vantagens em fazer uma estratificação na amostra e como realizá-la. Em seguida, faremos a estimação de quantidades de interesse a partir de amostras selecionadas após a estratificação. Outro aspecto importante que estudaremos é como realizar a alocação, ou seja, a distribuição da amostra nos estratos. Você vai perceber como é útil estratificar uma amostra antes de se realizar uma amostragem.
Por fim, apresentaremos o estimador baseado numa amostragem estratificada por variáveis de proporção, pois muitas vezes a natureza do estudo é qualitativa e variáveis do tipo proporção são necessárias.
Conceitos sobre amostragem estratificada
Geralmente, no mundo real, as populações encontradas são heterogêneas, isto é, há grande variabilidade entre as suas unidades em relação à média de uma variável X, por exemplo. Diante de situações em que se tem populações heterogêneas, a aplicação da amostragem aleatória simples pode acarretar em um tamanho de amostra elevado, tornando irrealizável a pesquisa pelo aumento do custo.
Exemplo
Imagine que você deseja fazer uma pesquisa sobre hábitos de vida da população brasileira. Você poderia fazer uma amostragem aleatória simples e selecionar pessoas ao longo do País. Porém, nesse caso, você teria pessoas espalhadas de forma aleatória em todo o território. Se você fosse selecionar 1000 pessoas, poderiam entrar poucas pessoas em alguns estados e muitas em outros. Ou pior, pode ser que vários estados, ou até mesmo regiões, ficassem de fora. Seria muito ruim fazer um levantamento sobre hábitos de vida dos brasileiros e sua amostra acabasse investigando 90% das pessoas que moram no Sudeste. Ou então selecionar duas pessoas em regiões muito distantes, o custo poderia não compensar a coleta de dois questionários.
Como resolver esse problema? A resposta é: Fazendo a estratificação.
O que deveríamos fazer seria selecionar uma amostra em cada um dos estados brasileiros ou pelo menos em cada uma das regiões. Parece bem mais intuitivo criar essas zonas de seleção do que selecionar pessoas de forma aleatória, não é mesmo?
Etapa 01
Fazendo isso, seria possível obter amostras específicas para esses locais e o melhor de tudo é que poderemos dar resultados para cada um desses locais também. Já que a pesquisa é sobre hábitos de vida, é muito mais interessante ter um resultado desagregado por região, ou ainda, por estado, do que algo único para todo o Brasil.
Etapa 02
Havendo informações a priori que possibilitem dividir as populações em partes, ou subconjuntos ou estratos, é possível usá-las de modo que pesquisando cada subconjunto ou estrato da população seja possível reduzir o erro de amostragem ou diminuir o tamanho da amostra.
Etapa 03
Isso permite que o erro amostral possa diminuir, pois como pesquisaremos em cada grupo de interesse, nenhum deles ficará vazio, logo o erro irá diminuir. Poderemos, ainda, utilizar, se possível, alguma variabilidade diferenciada em cada estrato, isso fará com que tenhamos amostras diferentes em cada estrato.
É muito comum que alguns objetivos de pesquisa queiram o conhecimento de características de partes ou subconjuntos das populações, por exemplo: Classificações, regionalização, divisões administrativas em situação urbana e rural etc. Nessas situações cada subconjunto da população também é tratado como estrato.
Definições básicas:
Existem alguns termos importantes a respeito dos tipos de estratos existentes e da forma como eles podem ser construídos.
Estratificação
O processo de estabelecer a divisão da população em subconjunto, de modo que cada elemento da população pertença somente a um subconjunto, é chamado de estratificação.
Estrato
O processo no qual cada subconjunto em que a população é particionada ou dividida é definido como sendo o estrato.
Estratos naturais
Quando os elementos da população são subdivididos em subconjuntos definidos por critérios geográficos, divisões político-administrativas, classes, categorias etc., diz-se que tais subgrupos constituem estratos naturais. A classificação dos estabelecimentos industriais, a divisão do Brasil em Unidades da Federação, a separação da população segundo a situação do domicílio em população urbana e rural são exemplos de estratos.
Estratos estatísticos
São definidos pelos estatísticos ou pesquisadores da área que tentam definir esses estratos como subgrupos mais homogêneos da população. A ideia é aumentar a eficiência na estimação. Quando os elementos da população são reunidos em subconjuntos definidos em função da dimensão de uma variável X, de modo a possibilitar o aumento da precisão da amostra com redução no seu tamanho, diz-se que tais subgrupos constituem estratos de tamanho, por exemplo. A classificação de indústrias segundo algumas faixas de produção ou a classificação dos estabelecimentos agropecuários em função da área total são exemplos de estratos de tamanho.
Exemplo real de pesquisa utilizando a estratificação
Na prática não utilizamos apenas uma forma de estratificação, podemos ter estratos naturais e de tamanho ao mesmo tempo. É muito comum utilizarmos essas definições conjuntas para aumentar ainda mais a qualidade da pesquisa.
Um exemplo interessante sobre isso é a pesquisa anual de serviços (PAS) do IBGE. De acordo com as notas técnicas da PAS em 2017, O objetivo contemplado no desenho da amostra foi a obtenção de estimativas dos totais populacionais referentes às variáveis investigadas de empresas de serviços, por Unidades da Federação e segundo os níveis de classificação de atividades definidos previamente. Além disso, a amostra da PAS é composta por dois tipos de estratos: Natural e final.
O natural é composto da combinação de Unidade de Federação e atividade econômica para cada uma das empresas. Depois que o estrato natural é construído, passa-se para o estrato de tamanho (estrato definido pelos estatísticos). Nesse caso, a distribuição das empresas em cada um desses estratos é dada pela quantidade de funcionários das empresas. Os estratos são definidos de acordo com o tamanho da empresa, empresas no estrato A1 (0 a 4 funcionários), estrato A2 (5 a 9 funcionários), estrato A3 (10 a 19 funcionários) e outro estrato com as empresas maiores, de 20 funcionários.
Na pesquisa da PAS teremos inicialmente os estratos naturais sendo os estados do Brasil e depois os estratos de tamanho de acordo com o porte da empresa (número de funcionários). Primeiramente, selecionam-se empresas em cada estrato natural (estado) e depois selecionam-se as empresas de acordo com o seu estrato de tamanho. É uma ótima forma de garantir representatividade por unidade da federação e por porte da empresa.
Vantagens da amostragem estratificada
A criação ou a utilização de estratos naturais já existentes traz uma série de vantagens na seleção amostral e, consequentemente, na divulgação dos resultados. Em relação aos aspectos positivos, podemos destacar:
A estratificação pode aumentar a precisão das estimativas para o conjunto da população. Ao comparar a amostragem estratificada (AE) com a amostragem aleatória simples (AAS), não necessariamente teremos uma amostra com erro menor.
De acordo com Bolfarine (2005), a simples utilização dos estratos por si só não produz necessariamente estimativas mais eficientes do que a AAS. Porém, se os estratos forem feitos de forma correta, consegue-se com o mesmo tamanho da amostra diminuir a variância do estimador. Esse é um resultado excelente, pois é possível ter uma amostra menor, com provavelmente um custo menor e, além disso, uma variabilidade menor.
Dado que os estratos foram definidos, você obrigatoriamente precisa selecionar amostras em cada um deles de forma independente. Assim, nenhum estrato pode ficar vazio. Dizemos que a seleção é feita de forma independente e os estratos são mutuamente excludentes, ou seja, um indivíduo não pode estar lotado em dois grupos (estratos) ao mesmo tempo.
Uma das maiores vantagens da amostragem estratificada é permitir a estimação para cada um dos grupos criados na pesquisa. Podemos então fazer a estimativa para cada um dos estratos e, caso o pesquisador tenha necessidade, ele pode estimar de forma diferente em cada estratificação realizada. Como os estratos são independentes, você logicamente pode estimar de forma independente também. Você pode querer a estimação de um total de um estrato e de uma média de outro, por exemplo.
Uma pesquisa realizada por AAS na qual a amostra é toda aleatorizada na população pode ser muito custosa, pois a população pode estar muito espalhada. Com a estratificação, podem-se limitar os grupos de interesse, simplificando a operação de coleta. Além disso, o gasto por unidade coletada diminui, já que não se coleta apenas uma unidade de um lugar, e sim vários indivíduos por estrato.
Desvantagens da amostragem estratificada
Nem tudo são flores, então não temos apenas pontos positivos na amostragem estratificada. Alguns autores não chamam nem de desvantagens da AE, preferem chamar de requisitos básicos para a realização desse tipo de seleção amostral. Entre os principais requisitos, temos:
Na pesquisa da PAS, cada empresa terá uma variável de unidade da federação, atividade econômica e quantidade de funcionários preenchida. Assim, primeiro se usa a variável de estrato da unidade da federação e atividade econômica para selecionar as empresas que farão parte da amostra e depois a quantidade de funcionários para distribuir essa amostra nos estratos.
Requer conhecimento das variáveis de estratificação para todas as unidades do cadastro antes da amostragem
É impossível construir uma pesquisa estratificada sem que exista essa variável construída no cadastro, pois é a partir dela que iremos selecionar a amostra. Nesse caso, precisamos que cada unidade amostral (aquele indivíduo que possa ser selecionado), tenha sua variável de estrato preenchida com todas as opções possíveis.
Dividir a população em muitos estratos pode levar à existência de amostras muito pequenas em cada estrato
Um ponto extremamente importante na amostragem estratificada é a boa construção das variáveis de estratificação. Se isso não for feito de maneira correta, pode ser que muitos estratos fiquem muito rarefeitos, ou seja, fiquem vazios. Um estrato vazio ou que conte com apenas uma empresa é muito ruim, pois não é possível calcular nenhum tipo de variância naquele estrato. A variância mede variabilidade, então como poderemos calcular isso com apenas um elemento? Não faz sentido calcular variância para apenas um indivíduo.

Teoria na prática
Ao se definir os estratos, deve-se verificar no cadastro se ele contém indivíduos suficientes que possam ser selecionados, pois além de não poder estimar variância, a estimativa de um total também fica muito limitada. Imagine o seguinte estrato de empresas da Tabela 1:
| Estrato | Empresa | Respondeu à pesquisa | Número de funcionários |
|---|---|---|---|
| 1 | A | Não | - |
| 1 | B | Não | - |
| 1 | C | SIM | 2 |
| 1 | D | Não | - |
Nesse estrato 1 temos 4 empresas, porém somente uma respondeu (empresa C) à pesquisa. Perceba como a quantidade de informações disponível nesse estrato é pobre. Não podemos calcular variância, pois existe apenas uma empresa, assim como não podemos estimar um total, por exemplo, pois estaríamos concentrando todo nosso resultado em apenas uma empresa.
O que fazer nesse caso?
Pode-se correr atrás das empresas que não responderam para tentar reverter a não coleta das informações, ou definir melhor esse estrato para que seu tamanho seja maior do que apenas 4 empresas.
Razões para estratificar
Há vários fatores importantes para se fazer a estratificação, entre os quais podemos enumerar:
1 - O desejo de aumentar a precisão das estimativas globais, dado que a variabilidade da característica de interesse pode ser grande. Essa melhora da precisão das estimativas pode ser feita reduzindo a variância dos estimadores após a construção dos estratos.
2- Garantir a divulgação das informações para cada domínio de interesse, ou seja, podemos obter estimativas para diversos segmentos da população. Assim, podemos fixar a precisão para cada estrato, e ter um melhor controle sobre os erros existentes.
3- Os estratos formam grupos naturais que podem ser de interesse. Pessoas que moram num determinado bairro podem ter hábitos de vida muito diferentes de outros bairros. Dessa forma, já existem naturalmente estratos que podem ser objetos de estudo.
4- Pode-se replicar na amostra a mesma composição da população de acordo com algumas características. Se soubermos que a população é formada por 52% de mulheres e 48% de homens e, além disso, temos 10% com nível superior, 50% com nível médio e 40% com nível fundamental, podemos criar uma amostra exatamente com essa mesma distribuição. A amostra será, então, criada de forma proporcional às variáveis na população.
5- Espalhar a amostra sobre a população. Como todos os estratos devem ter amostras selecionadas, esse processo de estratificação automaticamente espalha a amostra em cada um desses grupos amostrais.
Critério de eficiência
Para conseguir ganhar eficiência com o uso da estratificação, a ideia é tornar os valores da(s) variável(is) de estudo dentro de cada estrato os mais similares/homogêneos possíveis, isto é, minimizar a variância dentro dos estratos. A ideia da estratificação é, então, de criar estratos que sejam mais homogêneos entre si, ou seja, espera-se que dentro de cada estrato as populações ali existentes sejam semelhantes. Isso faz com que a variância dentro dos estratos seja menor enquanto a variância entre os estratos seja maior.
Comentário
Para que isso ocorra, é fundamental ter acesso a cadastro com variáveis auxiliares que possam ser usadas para estratificar a população de forma eficiente. Dessa forma, minimizaremos a variabilidade intraestratos e maximizaremos a variância entre os estratos.
Método geral
Primeiramente, deve-se particionar a população U em H subconjuntos mutuamente exclusivos e exaustivos chamados estratos. Dois eventos são chamados de mutuamente exclusivos quando eles não podem ocorrer ao mesmo tempo. Ao jogar uma moeda, os eventos podem ser cara ou coroa, mas nunca os dois simultaneamente. Já o termo exaustivo diz respeito ao fato de todas as categorias terem que ser contempladas com pelo menos uma unidade amostral.
Assim, as amostras têm que estar em apenas um estrato e todos os estratos devem ser contemplados com alguma amostra. Em notação matemática, temos a representação de cada estrato denotada por , assim temos , de modo que ... e . Seja o tamanho de , então .
Após estarem definidos os estratos populacionais, podemos selecionar uma amostra de tamanho , com , segundo uma seleção amostral independente dentro de cada estrato h, onde e . Assim, fica assegurado que cada estrato terá sua população representada na amostra final, pois .
Amostragem estratificada simples
Como vimos, a AE é um método em que os elementos da população serão divididos em grupos denominados por estratos. Vamos supor que nosso objetivo seja de fazer uma pesquisa sobre indústrias em uma região. Temos dois tipos de indústrias, as vermelhas e as azuis. Porém, as vermelhas são maioria, logo podemos a partir da população criar dois estratos, como pode ser visto na Figura 1.
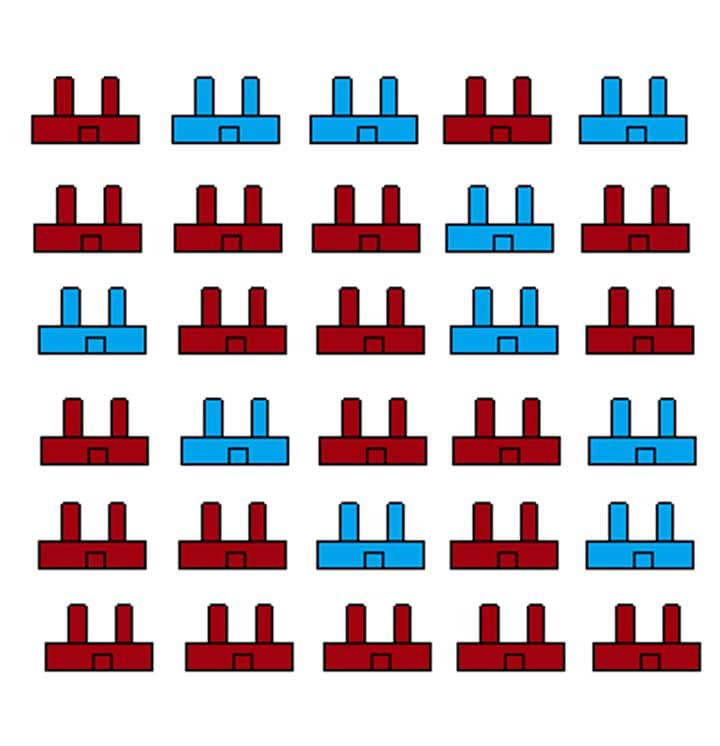

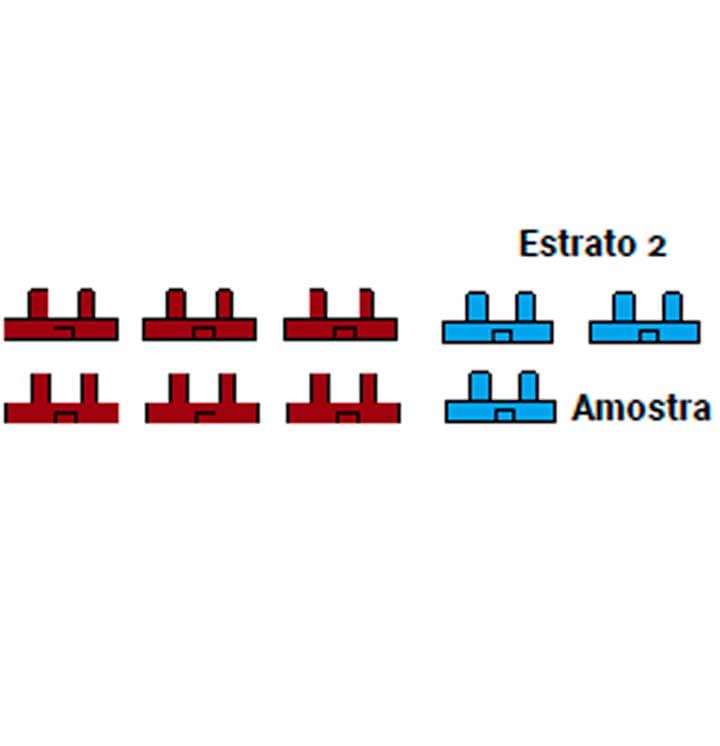
Após a criação dos estratos 1 e 2, podemos selecionar uma amostra que representa exatamente essa proporção populacional. Se tínhamos 2/3 de vermelhas e 1/3 de azuis, podemos selecionar em cada um dos estratos essa mesma proporção. Logo, se nossa amostra fosse de tamanho 9, teríamos 6 vermelhas e 3 azuis. Mas como iremos selecionar as empresas dentro de cada um dos estratos?
Nesse caso, faremos a amostragem aleatória simples.
Etapa 01
Na amostragem aleatória simples (AAS), fazemos uma seleção aleatória em que cada elemento tem igual probabilidade de ser sorteado para a amostra, e é selecionado independentemente de qualquer outro.
Etapa 02
Ou seja, utilizando um procedimento aleatório, sorteia-se com igual probabilidade um elemento da população. Dessa forma, uma amostra aleatória simples é retirada de cada estrato para representá-lo, de modo a possibilitar melhores estimativas da população.
Etapa 03
Essa é a forma mais usual da AE, pois primeiro fazemos a estratificação e, em seguida, selecionamos amostras em cada estrato por AAS constituindo a amostragem estratificada simples (AES).
O que é e para que serve a estratificação
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Definir as notações utilizadas na estratificação, com as expressões de estimação de totais, médias e variâncias na amostragem estratificada
Introdução
No módulo anterior, vimos todos os conceitos relacionados à amostragem estratificada, suas vantagens e desvantagens e quais os motivos para fazer a estratificação.
A partir deste módulo, vamos aprender como fazer estimações de variáveis de interesse e alocações de amostra utilizando a estratificação. Primeiramente, veremos o conceito de peso amostral, as notações e definições básicas e, logo em seguida, utilizaremos todas as expressões matemáticas para fazer as estimações na teoria da amostragem. Por fim, veremos como distribuir a amostra selecionada nos estratos de acordo com diferentes tipos de alocação amostral.
Peso amostral
Um conceito extremamente importante que é a base de planos amostrais mais elaborados é a ideia de peso amostral. O peso representa a importância que aquela unidade tem na população. Quando se faz uma amostra, apenas uma parte da população vai ser analisada, logo, é preciso um fator de ajuste para que os resultados amostrais sejam compatíveis e possam dar o resultado para a população. O peso amostral representa, então, o número de unidades da população que vão ser representadas por aquela unidade específica da amostra. Vamos ver um exemplo para entender isto melhor:
Imagine que você queira fazer uma pesquisa sobre o tempo dedicado aos estudos (yi) de uma certa população que tenha 120 pessoas. Como você aprendeu sobre estratificação, você decide criar estratos para separar os diferentes níveis de instrução. Usaremos o índice h para denotar a quantidade de estratos, no exemplo, temos 3 estratos, logo h = 3.
Etapa 01
Inicialmente você constrói, então, 3 estratos:
- Estrato 1 ‒ Nível fundamental
- Estrato 2 ‒ Nível médio
- Estrato 3 ‒ Nível superior
Ao consultar o cadastro da população, você descobre que existem 70 pessoas de nível fundamental, 30 de nível médio e 20 de nível superior. Como seu tempo está escasso, você não consegue entrevistar todas as 120 pessoas, e faz uma amostragem para selecionar apenas 20 indivíduos.
Etapa 02
A tabela abaixo resume os níveis de estudo de cada indivíduo obtido na amostra e seu respectivo estrato:
| Indivíduo | Estrato (Nível de estudo) | Tempo de estudo diário (horas) |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 0.5 |
| 3 | 1 | 0.3 |
| 4 | 1 | 0 |
| 5 | 1 | 0.4 |
| 6 | 1 | 1 |
| 7 | 1 | 0.2 |
| 8 | 1 | 0.9 |
| 9 | 1 | 2 |
| 10 | 1 | 1.5 |
| 11 | 1 | 1 |
| 12 | 2 | 1.1 |
| 13 | 2 | 1.5 |
| 14 | 2 | 1.3 |
| 15 | 2 | 1.6 |
| 16 | 2 | 2 |
| 17 | 3 | 2 |
| 18 | 3 | 3 |
| 19 | 3 | 4 |
| 20 | 3 | 10 |
Etapa 03
Com essa tabela, você decide fazer a média do tempo de estudos de todos os indivíduos. Somando todos os valores e dividindo por n = 20, você encontra o valor médio de 2,565 horas de estudo. Vamos pensar um pouco, você acha justo fazer uma média geral única sabendo que existem estratos diferentes e, além disso, o total da população em cada estrato também é diferente?
Vamos encontrar a média por estrato. Somando os valores e dividindo pela quantidade de amostra em cada estrato temos:
- Estrato 1:
- Estrato 2:
- Estrato 3:
Temos agora um valor médio por estrato, isso já é um resultado bem interessante e que faz bem mais sentido que aquele resultado anterior obtido. Mas, e se quisermos uma média geral, como devemos proceder?
Resposta
Nesse caso, vamos levar em consideração o tamanho populacional de cada estrato. Para isso, usaremos a quantidade da população como fator no cálculo da média geral, ou seja, , e . Com esses fatores, faremos uma espécie de média ponderada com a participação de cada estrato:
Portanto, a média geral é feita levando em consideração a estratificação. Esse é o valor correto para a média geral, e não aquele anterior, ignorando todos os estratos. O que estamos fazendo aqui é levar em consideração a participação (no cálculo da média) do tamanho de cada estrato populacional. Ou seja, se sabemos que existem mais pessoas de nível fundamental, temos que dar maior "peso" a essa resposta.
Esse fator que utilizamos de nos dá exatamente essa ideia de peso amostral, ou seja, é uma ponderação correspondente à fração de elementos existentes na população em relação ao total N. Essa fração amostral é muito utilizada na prática e chamada de , logo, toda vez que precisarmos considerar o tamanho de algum estrato em relação ao total, faremos a divisão do seu total pelo total geral e chamaremos o resultado de .
Notação básica e estimação
A amostragem estratificada utiliza de muitas variáveis na construção das expressões usadas no processo de estimação. Para a população, chamamos essas variáveis de interesse de parâmetros. Nosso objetivo, então, é conseguir estimar esses parâmetros populacionais através da amostra. Para identificar as unidades, usaremos a seguinte notação:
- Um identificador h (h = 1, ... , H) para indicar o estrato a que pertence.
- Um identificador i (i = 1, ... , ) para indicar a unidade dentro do estrato.
- O valor de alguma variável da pesquisa chamamos de , para i = 1,... , e h = 1,...,H.
- Os tamanhos populacionais são dados por: + + ... .
- Os tamanhos amostrais são dados por: + + ... .
Parâmetros popula cionais
Estimação dos parâmetros populacionais
As expressões acima são referentes aos valores populacionais, porém, na prática, iremos trabalhar com amostras. Como a amostragem é feita independente por estrato, podemos estimar de forma separada os parâmetros de cada estrato. Portanto, a estimação da amostragem estratificada com seleção das unidades amostrais por amostragem aleatória simples com reposição é dada por:
Vejamos um exemplo prático de como fazer essas estimações:
Uma empresa de tecnologia está interessada em conhecer o comportamento dos usuários de uma pequena cidade no que diz respeito ao acesso à internet. Para isso, ela contratou uma equipe para fazer uma pesquisa, de modo que consiga estimar o número médio de horas que os moradores permaneçam online.
Ao todo, foram entrevistadas 80 pessoas selecionadas sob o esquema de amostragem estratificada simples com reposição. O município está dividido em quatro áreas: Área A, área B, área C e área D. As áreas A, B e C são consideradas urbanas, enquanto a área D é rural. Existem 620 moradores na cidade, divididos da seguinte forma: 310 na área A, 155 na área B, 93 na área C e 62 na área D.
O tamanho de amostra selecionado foi diferente entre os estratos. A tabela abaixo resume os pesos de cada estrato, o tamanho selecionado, a média e a variância encontrada.
| Áreas | ||||
|---|---|---|---|---|
| A | 40 | 30 | 5 | |
| B | 20 | 25 | 16 | |
| C | 12 | 23 | 13 | |
| D | 8 | 19 | 9,5 |
Etapa 01
Vamos encontrar agora a estimativa da média populacional do número de horas que os moradores acessam a internet. Para isso, vamos utilizar a expressão
Portanto, em média, as pessoas dessa cidade ficam conectadas 26,6 horas.
Etapa 02
Da mesma forma que encontramos o estimador da média amostral, podemos encontrar a estimativa de sua variância. Assim, fazemos
Encontrando o erro padrão, temos . Ou seja, o erro médio da estimativa é um pouco mais de 1 hora por dia de uso da internet.
Alocação da amostra
Vimos até o momento como realizar o procedimento de estimação de acordo com uma amostra que já havia sido definida para os estratos. Agora, vamos entender como é feita a distribuição das n unidades da amostra pelos estratos. Esse processo chama-se alocação da amostra e é bem importante, pois garante a precisão do procedimento amostral.
Temos três principais formas de distribuir a amostra através dos estratos. Essa alocação é feita, em geral, a partir do conhecimento dos pesquisadores ou do conhecimento prévio das variáveis envolvidas. Assim, temos:
Alocação uniforme
Na amostragem estratificada uniforme, temos o mesmo tamanho de amostra para cada estrato. É a alocação mais simples e básica e, apesar de ser a mais intuitiva, pode não ser a melhor escolha em termos de eficiência.
Imagine que sua população seja dividida em três cores, porém não é uma divisão igual. Na hora de se fazer uma AE com alocação uniforme, a amostra distribui-se de forma exatamente igual. Assim, para cada estrato h:
Onde k representa o número de estratos.
O tamanho global da amostra é dividido pelo número k de estratos. Então, se você tiver um tamanho de amostra de 90 e 3 níveis de estratos, a amostra em cada estrato será:
Simplesmente divide-se o total da amostra pela quantidade de estratos.
Alocação proporcional
Outra forma de fazer a distribuição é pelo critério que mantém a fração da amostragem em cada estrato h igual à fração populacional. Ou seja, nesse tipo de alocação, a amostra previamente definida de tamanho n é distribuída proporcionalmente ao tamanho dos estratos.
Perceba como a amostra reflete exatamente a estrutura da população. Se existem 75% de indivíduos azuis na população, logo deve haver exatamente 75% de indivíduos azuis na amostra também. E assim sucessivamente para todos os estratos. É uma forma um pouco mais justa de distribuir a amostra pelos estratos. Assim, temos:
Imagine que, em uma pesquisa, você tenha na população 800 famílias na zona urbana e 300 famílias na zona rural (total populacional -> N = 800 + 300 = 1100 famílias). Se o total de uma amostra a ser selecionado é de 90 famílias, fazemos:
Dessa forma, com a alocação proporcional e arredondando os valores para cima, teremos n= 91 famílias com 66 do estrato 1 (urbano) e 25 do estrato 2 (rural). Basicamente, replicamos a estrutura populacional na amostra.
Alocação ótima de Neyman
Esse é um método mais sofisticado de alocação das amostras nos estratos. Como o próprio nome diz, ele é ótimo, ou seja, apresenta um resultado bastante interessante. Nesse caso, a distribuição da amostra não é feita somente pensando na proporção existente na população, mas também na sua variabilidade.
Na alocação de Neyman, a variabilidade da variável de interesse também é levada em consideração, pois se ela for mais homogênea na população, não precisaremos de amostras muito grandes naquele estrato. Ou seja, essa distribuição leva em consideração a dispersão da variável na população. Assim, os tamanhos serão proporcionais aos da população e também aos desvios padrões da característica Y em cada estrato h. A expressão é dada por:
Onde n representa o tamanho da amostra, representa o desvio padrão da variável y no estrato h e representa o tamanho do estrato h.
Perceba nesse caso como a distribuição da amostra não segue o padrão populacional. Isso ocorreu porque a variabilidade dos indivíduos vermelhos era maior que a dos azuis. Assim, precisamos de uma amostra maior vermelha do que azul. Dessa forma, a estrutura da amostra leva em consideração não apenas o tamanho populacional como também sua variabilidade. Vamos ver um exemplo:

Teoria na prática
Uma população de tamanho 20 é dividida em 2 estratos, 8 no estrato 1, 12 no estrato 2. O desvio padrão do estrato 1 é de e . Se uma amostra de tamanho 10 for selecionada, como seria a distribuição em cada um dos estratos?
Ao somar e temos 10, porém temos que decidir se arredondamos ambos para cima ou não. Se for feito para cima, teremos e . A amostra passaria a ser 11, esse valor seria o mais correto, porém, se não puder fazer uma amostra de 11, recomenda-se arredondar para cima o estrato de menor tamanho, pois já que é baixo, melhor ter um valor acima. Teríamos, então, e .
Conceitos auxiliares para estimação
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Definir variáveis de proporção e o tamanho de amostra utilizado na amostragem estratificada simples com as diferentes alocações disponíveis
Introdução
Vimos no módulo anterior como estimar quantidades de interesse em uma pesquisa, totais e médias, por exemplo, no caso da amostragem estratificada simples. Além disso, vimos como estimar a variância e o erro padrão para essas estimativas. Em seguida, entendemos como fazer a alocação da amostra em cada um dos estratos de acordo com a escolha entre uniforme, proporcional ou Neyman.
Agora, veremos como dimensionar o tamanho da amostra para o plano amostral da amostragem estratificada. Além disso, veremos também como fazer as estimações para variáveis do tipo proporção, nas quais o interesse é estudar a ocorrência de alguma característica da população.
Estimação de proporções na amostragem estratificada
Além de variáveis quantitativas, uma pesquisa também pode conter variáveis qualitativas. O tratamento relativo à estimação dos dados e o cálculo do tamanho amostral são feitos de forma diferente. Às vezes, deseja-se estimar a proporção ou a percentagem de unidades da população que possuem certa característica e atributo ou que se integram em determinada categoria. Muitos dos resultados dos censos e levantamentos assumem essa forma, como, por exemplo, a proporção de pessoas que pegaram empréstimo no banco, a percentagem da população constituída de estrangeiros etc.
Saiba mais
Basicamente, a variável de proporção é uma razão entre o número de unidades de uma população com uma determinada característica e total de unidades dessa população. O denominador é sempre o número de unidades da população e o resultado da proporção está sempre entre 0 e 1, podendo ser representado em porcentagem.
Em variáveis qualitativas, não podemos fazer nenhum tipo de cálculo, já que isso é restrito somente às variáveis quantitativas. O que podemos fazer nesse caso é contar quantos indivíduos têm aquela característica na população. Dessa forma, criamos uma variável y, por exemplo, que recebe valor para cada unidade com aquela característica e
Na amostragem estratificada, teremos que fazer a soma de y_i em cada um dos estratos que foram construídos. Se quisermos estimar a proporção de unidades na população que se enquadram em alguma classe C definida, a estratificação ideal seria aquela em que no primeiro estrato estivessem todos ou a maioria dos indivíduos com aquela característica, e no outro estrato, os indivíduos que não apresentam essa mesma característica (ou apresentam pouca).
Exemplo
Por exemplo, queremos fazer uma pesquisa para estimar a proporção de várias características de pessoas que frequentam shopping. O ideal seria no estrato 1 haver somente pessoas que frequentam shopping e no estrato 2 os demais indivíduos.
Como podemos estimar de forma independente em cada estrato, seria muito interessante ter estratos bem diferenciados no que diz respeito à nossa variável de interesse. Para efeitos práticos você conseguiria os melhores resultados caso fizesse isso, porque seria possível estimar em cada estrato (um com a característica e outro sem) e depois fazer comparações. Por isso, dizemos que a etapa da construção dos estratos é um ponto fundamental da pesquisa, que pode afetar a eficácia dos resultados.
Com os valores de uma amostra em cada um dos estratos h podemos estimar a proporção populacional, a variância da proporção e seu erro padrão através da amostragem estratificada simples sem reposição, da seguinte forma:
A estimativa da proporção em toda a população, ou seja, para todos os estratos simultaneamente na amostragem aleatória estratificada é dada por:
Pelas expressões acima, você pode ver que a proporção comporta-se como se fosse uma média ponderada, levando em consideração o peso de cada estrato na população, só que ao invés de somar os valores das variáveis, somam-se os para cada estrato e indivíduo e depois divide-se pelo total.
Vamos ver um exemplo de estimação da proporção para entendermos como isso acontece na prática.
Exemplo
Seja uma amostra estratificada simples de 400 crianças menores de 6 meses de um certo hospital. Dados da maternidade sugerem a construção de dois estratos de acordo com a utilização ou não de incubadora após o nascimento. No estrato 1, ficaram os bebês que tiveram assistência neonatal com um total de crianças. Já no estrato 2 ficaram os bebês que não precisaram de internação, perfazendo um total de crianças. Foi perguntado para os pais se cada um desses bebês tinha tomado as primeiras vacinas. No estrato 1, 328 bebês tinham tomado e no estrato 2 foram 406 bebês. Qual a proporção de bebês que tomaram a vacina e qual o erro padrão da medida na amostragem estratificada com alocação proporcional?
Etapa 01
Inicialmente, sabemos que o total populacional é de bebês. O peso amostral do estrato 1 é de e. Além disso, a proporção amostral dos bebês que tomaram a vacina é de e . Agora, podemos encontrar a estimativa da proporção, assim faremos =
Etapa 02
Como fizemos a alocação proporcional, sabemos que do total de 400 bebês temos , assim, e . Ou seja, a amostra do estrato 1 foi de 132 bebês e a amostra do estrato 2 foi de 268 bebês. Para encontrar o erro padrão, precisamos primeiro encontrar a variância. Logo, fazemos
Etapa 03
Fazendo a raiz da variância, encontramos o valor de . Ou seja, o erro padrão da estimativa é de 0,02 e como é uma proporção, temos, então, um erro de cerca de 2% dos bebês.
Tamanho da amostra
No planejamento de uma pesquisa, o cálculo do tamanho de amostra é uma etapa muito importante. Um desenho amostral com uma quantidade de respondentes muito grande pode implicar em desperdício de recursos, enquanto uma amostra muito pequena pode diminuir a qualidade dos resultados. A decisão nem sempre pode ser feita de forma satisfatória e é preciso tomar decisões baseado no orçamento disponível e na qualidade que se deseja.
O método mais básico de seleção de amostragem é a aleatória simples (AAS). Nesse plano amostral, todas as unidades amostrais têm a mesma probabilidade de serem selecionadas. Já na amostragem estratificada, esse valor é alterado de acordo com o estrato de origem da unidade. Se formos retirar a mesma quantidade de amostra em cada um dos estratos por AAS, é natural que estratos maiores tenham unidades de seleção com probabilidade menor de serem selecionadas e estratos pequenos tenham unidades com probabilidade maior, pois sua população é menor. Esse peso da amostra é uma variável importante e precisa ser levado em consideração no momento de se realizar os cálculos de tamanhos amostrais.

Teoria na prática
Imagine, por exemplo, que se deseja retirar uma amostra de 5 indivíduos de 3 estratos referentes a classes sociais. No estrato 1 há indivíduos, no estrato 2 há indivíduos, e no estrato 3 há indivíduos. A probabilidade de seleção do estrato 1 é de ; e . Perceba que estratos menores apresentam maiores probabilidades de seleção. Porém, na prática, para encontrarmos o tamanho da amostragem estratificada, seguiremos os seguintes passos:
1 - Identificaremos qual a variável que estamos interessados em investigar: É uma média? Um total? Uma proporção?
2- Após a identificação da variável do estudo, usaremos as expressões específicas de cada variável para encontrarmos o tamanho de amostra.
3 - Por fim, com o tamanho total da amostra, utilizaremos a alocação para distribuir essa amostra nos estratos. No final, a soma das amostras de cada estrato tem que ser igual ao tamanho total da amostra.
Vamos ver então como calcular o tamanho da amostra baseado em médias, totais e proporções e suas diferentes alocações.
Tamanho de amostra para estimação da média na amostragem estratificada
Se o interesse da pesquisa for responder a questões ligadas a médias de determinadas variáveis, temos que utilizar um conjunto de expressões específicas para o tamanho da amostra. Essas expressões variam conforme a alocação da amostra foi pensada no momento da construção da pesquisa. A expressão geral para o tamanho de amostra na amostragem estratificada para a estimação da média é dada por:
onde e é uma constante que define o tipo de alocação utilizado. Porém, não utilizaremos simplesmente a fórmula acima, pois ao fazer as alocações na amostra, podemos já encontrar as expressões específicas para cada caso. Assim, as fórmulas mudam de acordo com a alocação escolhida. Vamos tratar aqui das duas distribuições amostrais mais utilizadas, que é o caso da proporcional e da ótima de Neyman.
Alocação proporcional
Para uma amostragem estratificada com alocação proporcional, temos a seguinte expressão para o tamanho da amostra:
Onde V é a variância mínima desejada para estimar a média da população. Essa variância está em função da margem de erro "d" e do valor z da tabela normal. Caso não seja dada, pode ser calculada por:
Ou seja, neste caso, primeiramente calculamos e depois calculamos n. Poderíamos fazer a substituição e ter apenas uma fórmula, mas de acordo com Cochran (1977), fazer essa separação traz ganhos em termos computacionais.
Vamos ver um exemplo prático para entender como o tamanho amostral seria calculado nesse caso.
Exemplo
Uma empresa de minério de ferro está interessada em estimar a quantidade média de um tipo de ferro em uma nova placa que está produzindo. O ferro utilizado é dividido em três tipos para que a componente fique mais resistente e menos oxidativa (tipo I, tipo II e tipo III). Pesquisas anteriores já tinham avaliado a variância desses tipos de ferro nessas placas e a variância encontrada foi para o tipo I, para o tipo II e para o tipo III. Outro dado fornecido foi a quantidade de ferro produzido de cada tipo: 13800T para o tipo I, 23400T para o tipo II e 22800T para o tipo III. A variância mínima V estabelecida foi de 0,02. Qual o tamanho de amostra mínimo necessário, dado que queremos uma alocação proporcional em cada estrato?
Etapa 01
Para responder a essa questão, precisamos encontrar primeiramente o peso de cada estrato, ou seja, o valor . Assim, fazemos:
Etapa 02
Com o peso encontrado, podemos encontrar fazendo:
Etapa 03
A partir de , podemos encontrar n. Logo,
Arredondando para cima, temos então um tamanho de amostra de 74 placas de ferro para essa pesquisa.
Alocação ótima de Neyman
A outra forma de distribuição amostral nos estratos que vimos foi a alocação ótima de Neyman. Como ela leva em consideração a variabilidade de cada estrato, acaba sendo preferida, se possível, na utilização prática da amostragem estratificada. Assim, para uma AE com alocação ótima de Neyman, para estimação da média, temos a seguinte expressão para o tamanho da amostra:
Tamanho de amostra para estimação do total na amostragem estratificada
Da mesma forma que fizemos para a estimação da média, podemos fazer os cálculos do tamanho de amostra caso nossa variável de interesse seja estimar um total populacional. Os resultados são bem semelhantes. Novamente, as expressões variam conforme a alocação da amostra foi pensada no momento da construção da pesquisa.
O caso geral é dado por:
Onde e é uma constante que define o tipo de alocação utilizado. Porém, não utilizaremos simplesmente a fórmula acima, pois ao fazer as alocações na amostra, podemos já encontrar as expressões específicas para cada caso. Assim, as fórmulas mudam de acordo com a alocação escolhida. Vamos tratar novamente aqui das duas distribuições amostrais mais utilizadas, que é o caso da proporcional e da ótima de Neyman e a variância V é dada por:
Alocação proporcional
No caso da amostragem estratificada com alocação proporcional, o peso do estrato e o percentual de amostra em cada estrato têm o mesmo valor. Se tiver 30% do estrato A na população, teremos 30% da amostra como sendo de A. Assim, . Substituindo esse valor na expressão do caso geral, temos o seguinte resultado para o tamanho da amostra no caso de um total populacional:
Alocação ótima de Neyman
Da mesma forma que fizemos na alocação de Neyman para a média, podemos fazer para o total também. Nesse caso, o peso amostral fica em função da variabilidade de cada um dos estratos. Portanto, temos a seguinte expressão para o cálculo do tamanho de amostra na alocação ótima de Neyman:
Tamanho de amostra para estimação da proporção
Se o interesse da pesquisa for responder a questões qualitativas, deve-se pensar no cálculo amostral utilizando a proporção. As fórmulas são semelhantes aos casos anteriores, em que devemos apenas substituir as variáveis de média ou total por variáveis de proporção. Essas expressões também variam conforme a alocação da amostra foi pensada no momento da construção da pesquisa.
Alocação proporcional
Para uma amostragem estratificada com alocação proporcional, temos a seguinte expressão para o tamanho da amostra no caso da proporção:
Onde V é a variância mínima desejada para estimar a proporção da população. Essa variância está em função da margem de erro "d" e do valor z da tabela normal. Caso não seja dada, pode ser calculada por
Alocação ótima de Neyman
Da mesma forma que fizemos na alocação de Neyman para a média e para o total, podemos fazer também para a proporção. Nesse caso, o peso amostral fica em função da variabilidade de cada um dos estratos. Portanto, temos a seguinte expressão para o cálculo do tamanho de amostra na alocação ótima de Neyman:
Novamente, as fórmulas de n e
Exercícios
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Ao longo dos módulos, foi possível entender mais sobre o método de amostragem estratificada, as formas de construção dos estratos e de como isso pode melhorar os resultados da pesquisa.
Inicialmente, discutimos os conceitos fundamentais da amostragem estratificada simples, ou seja, a amostragem estratificada permite a construção dos estratos e, depois, em cada estrato, são selecionadas amostras por meio da amostragem aleatória simples.
No segundo módulo, apresentamos as ferramentas estatísticas de estimação das quantidades de interesse. Aprendemos como estimar um total e uma média a partir de uma amostra estratificada e também as estimativas de variância dessas medidas. Além disso, vimos como distribuir a amostra nos estratos, ou seja, fazer a alocação amostral. Vimos que a partilha pode ser feita de forma uniforme, proporcional ou pela forma ótima de Neyman, sendo esse último caso aquele que garante melhor precisão dos resultados.
Por fim, investigamos também a estimação de proporções no caso da amostragem estratificada, já que em determinadas pesquisas o foco em variáveis qualitativas pode ser de maior interesse do que em variáveis quantitativas. Outro assunto importante que vimos juntos foi o cálculo do tamanho de amostra para fazer as estimações. Conhecemos as expressões utilizadas para se definir uma amostra para estimar totais, médias, proporções e de como a alocação pode afetar esse dimensionamento.
Assim, temos certeza de que, ao chegar ao fim deste tema, o estudante entendeu a importância de se fazer uma estratificação e como fazer estimativas das variáveis de interesse.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Descreveu o método de seleção por amostragem aleatória estratificada, a importância da utilização de estratos e as razões para estratificação
Definiu as notações utilizadas na estratificação, com as expressões de estimação de totais, médias e variâncias na amostragem estratificada
Definiu variáveis de proporção e o tamanho de amostra utilizado na amostragem estratificada simples com as diferentes alocações disponíveis