Descrição
Abordagem didático-pedagógica sobre a natureza da luz, os conceitos de onda eletromagnética, a dualidade onda-partícula, produção dos raios X e suas aplicações.
PROPÓSITO
Quando você sintoniza seu rádio, assiste à TV, envia uma mensagem de texto, coloca pipoca em um forno de micro-ondas ou faz uma imagem radiográfica, está usando energia eletromagnética; logo, conhecer e entender a natureza contemporânea da luz e a extensa gama do nosso espectro eletromagnético é essencial para que as aplicações sejam direcionadas de maneira correta e segura.
OBJETIVOS
Módulo 1
Analisar a natureza ondulatória da luz e o espectro eletromagnético em termos de frequência e comprimento de onda
Módulo 2
Identificar a natureza da luz na visão contemporânea e seu comportamento ondulatório e/ou corpuscular (dualidade onda-partícula)
Módulo 3
Reconhecer a produção dos raios X e a importância de suas aplicações em diversas áreas
Introdução
A beleza de um recife de corais, o brilho quente do sol, a ardência das queimaduras solares, os raios X revelando um osso fraturado, e até mesmo a pipoca de micro-ondas – tudo isso é trazido até nós por ondas eletromagnéticas.
A lista dos vários tipos de ondas eletromagnéticas, desde ondas de transmissão de rádio até emissões nucleares de raios gama (raios ), é intrigante e deslumbrante por si só. Ainda mais intrigante é que todos esses diferentes fenômenos são manifestações da mesma natureza.
Mas o que são ondas eletromagnéticas? Como elas são criadas e como viajam? Como podemos entender suas propriedades amplamente variáveis? Qual a relação entre efeitos elétricos e magnéticos? Essas e outras questões serão exploradas neste conteúdo.
As especulações sobre a natureza da luz apareceram nos primórdios da Humanidade. Demócrito foi um filósofo grego que viveu entre 460 e 370 a.C. Antes de se estabelecer na Grécia, ele viajou inúmeras vezes pelo Egito e por outros lugares, tendo como mestre principal Leucipo (490 a.C.). Demócrito absorveu o conceito de atomismo na Ásia Menor.
Os atomistas afirmavam que toda matéria era composta de partículas minúsculas, infinitamente pequenas, tão pequenas que nenhuma matéria poderia ser menor do que isso. Essas partículas seriam indivisíveis e chamadas de átomos, do grego “indivisível”.
Para os filósofos, os átomos seriam eternos, imutáveis, indestrutíveis e apenas suas propriedades físicas difeririam umas das outras. Em particular, a luz associada ao fogo seria composta de átomos pontiagudos (tetraedros), de forma a causar queimaduras dolorosas. O modelo corpuscular de Demócrito era baseado na intuição e na pureza de pensamentos, uma filosofia chamada de filosofia moral .
Aristóteles (384-322 a.C.), discípulo de Platão, introduziu a teoria sensorial e natural, conhecida atualmente como Ciência. Sua teoria tinha como instrumento os órgãos sensoriais, uma vez que não havia outros tipos de sensores naquela época. Aristóteles propôs uma explicação para a luz, similar à que ele havia dado às vibrações sonoras, percebidas pelos ouvidos e pelo tato.
Segundo ele, um objeto luminoso vibra, fazendo com que um meio incerto fique em estado de vibração, que o filósofo denominou de diáfano, o que faz com que o movimento das emoções entre nos componentes do olho. O modelo não se baseava em nenhuma observação do fenômeno, fato que seria muito difícil para a época. Era uma analogia baseada exclusivamente em associações.
Como podemos ver, os gregos tinham muitas ideias, mas não possuíam uma tradição experimental de fazer observações físicas da natureza. Na maioria das vezes, fenômenos naturais comuns não podiam ser investigados com os meios de que se dispunha e, portanto, qualquer argumento era bom, desde que fosse bem definido.
No módulo 1, serão descritas as mais bem fundamentadas teorias para a natureza ondulatória da luz, assim como a definição das ondas eletromagnéticas e seu espectro; no módulo 2, as características corpusculares e a dualidade onda-partícula; e, na sequência, no módulo 3, detalharemos a produção, as características e aplicações dos raios X.
MÓDULO 1
Analisar a natureza ondulatória da luz e o espectro eletromagnético em termos de frequência e comprimento de onda
Filosofia moral
A história neoplatônica (filosofia moral) dominou o fim da Antiguidade e a primeira metade da Idade Média, tanto na Europa quanto nos países muçulmanos. No final desse período, uma importante obra marcou a óptica geométrica e rejeitou completamente o raio visual: a do iraquiano Ibn al-Haytham; ele não ofereceu nenhuma reflexão sobre a natureza da luz.
Essa situação se perpetuou por muito tempo e só mudou no renascimento europeu. Obras importantes, como as de Roger Bacon (1220-1292) e de Robert Grosseteste (1175-1253), sintetizaram o ponto de vista do sábio iraquiano e os conceitos pré-ondulatórios de Aristóteles. Pela primeira vez, várias preocupações foram previamente reunidas em trabalhos escritos.
NATUREZA ONDULATÓRIA DA LUZ
O grande sucesso do telescópio refrativo de Galileu, em 1609, deu início a uma nova fase no estudo da luz. Desde o início, foram observados alguns fenômenos que não podiam ser compreendidos pela óptica geométrica. No modelo de propagação retilínea da luz, um obstáculo deveria proporcionar uma região de sombra de contornos nítidos.
A projeção dessa sombra em uma parede, pelas previsões do modelo geométrico, seria caracterizada por uma região escura claramente separada da região iluminada pela fonte luminosa. É claro que, para isso, deveríamos levar em consideração a região de penumbra, causada pelo tamanho físico da fonte de luz, e que deveria ser a menor possível para se fazer uma observação apurada.

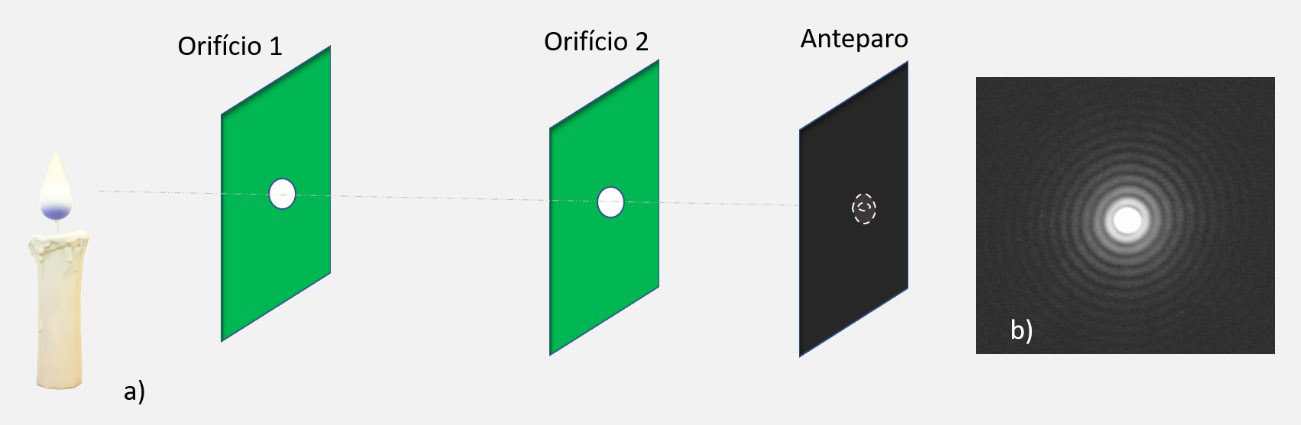
As primeiras experiências logo mostraram a existência de faixas claras, onde devia haver sombra; e, de faixas escuras, onde devia estar bem iluminado. A imagem a seguir, ilustra:
- Uma montagem experimental para observação no orifício 2 , em a).
- Em b), a imagem observada no anteparo.
Orifício 2
Esse orifício, cuja imagem é projetada sobre um anteparo, é iluminado por uma fonte pontual de luz construída a partir de uma fonte de luz extensa e do orifício 1.
Saiba mais
Essas imagens podem ser obtidas com orifícios na ordem de 1mm de diâmetro sobre um anteparo a 1m de distância. Essas falhas nas previsões da óptica geométrica foram denominadas de difração por Francesco Maria Grimaldi (1618-1663), jesuíta e professor da Universidade de Bolonha.

As primeiras referências à difração aparecem nas anotações de Leonardo da Vinci (1452-1519), cerca de cem anos antes de Galileu apresentar seu telescópio.
No entanto, as primeiras anotações publicadas só ocorreram após a morte de Grimaldi, em 1663, quando seus trabalhos foram divulgados.

Para explicar o desvio da luz de sua trajetória retilínea, Grimaldi recorreu à experiência comum relativa à propagação das ondas sonoras ou das ondas sobre a superfície da água, como na imagem ao lado. O som não pode ser barrado por um muro não muito alto, mesmo que seja muito espesso, pois as ondas sonoras ao passarem por cima dele se desviam parcialmente em direção ao solo, contornando-o.
Da mesma forma, as ondas do oceano, ao penetrarem em um porto, atingem não apenas os barcos que estejam diante da entrada, mas também aqueles localizados nas suas áreas protegidas.
Christiaan Huygens (1629-1695), filho de um importante oficial do governo holandês, já possuía uma grande reputação científica em 1678, com seus trabalhos em Astronomia e Física. Nesse ano, Huygens propôs uma teoria ondulatória para a luz.
Como a natureza própria da luz era totalmente desconhecida, Huygens interpretava a luz em termos de ondas longitudinais, como:
Entretanto, esse detalhe não traz nenhuma consequência no que se refere à propagação de ondas.
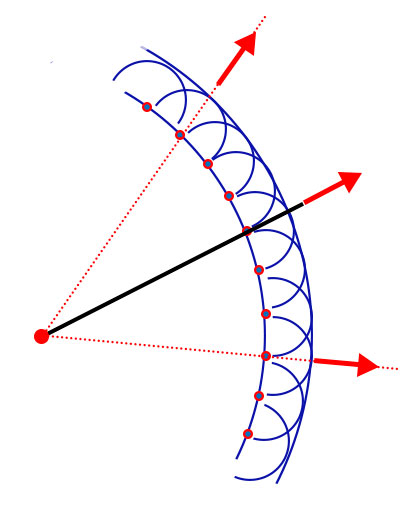
No modelo de Huygens, cada ponto em uma frente de onda é tratado como uma fonte de uma onda esférica denominada ondícula secundária ou ondícula de Huygens. O envoltório dessas ondículas, em um instante posterior, é determinado pela tangente a essas superfícies. O envoltório é assumido como a nova posição da frente de onda.
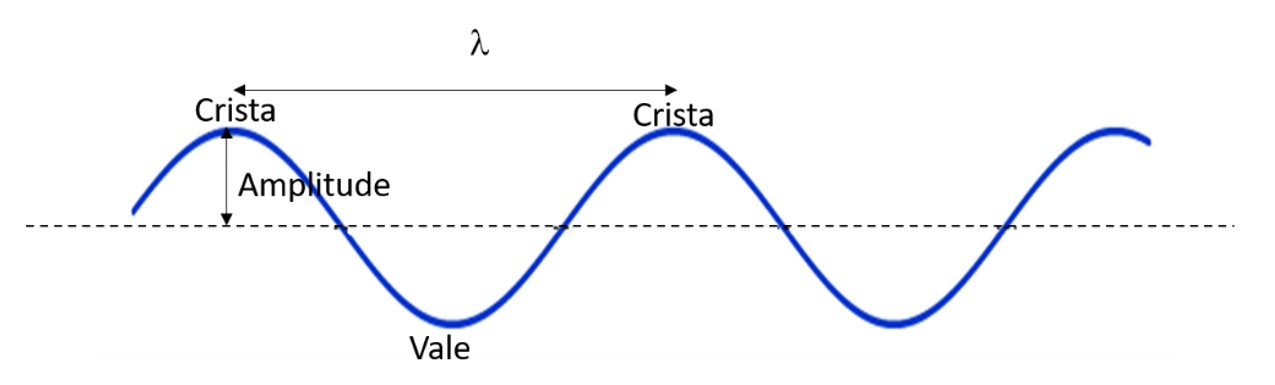
Uma onda é caracterizada pelo seu comprimento de onda que pode ser visualizado pela distância entre duas cristas da onda e pela frequência de suas oscilações, como na imagem a seguir. Essas duas grandezas são relacionadas através da velocidade v de propagação da onda na forma:
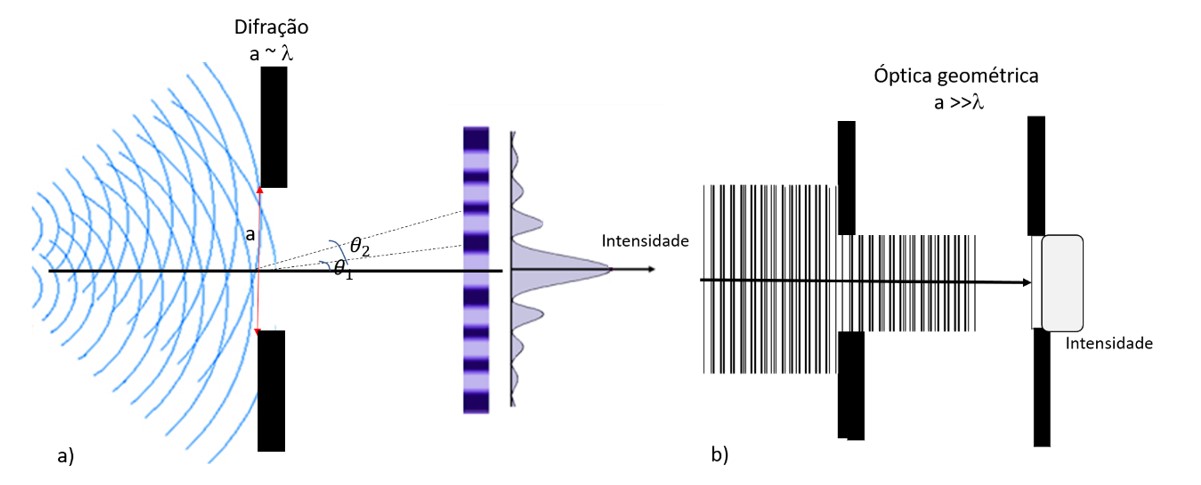
O fenômeno da difração pode ser mais bem observado quando as dimensões do obstáculo são comparáveis com o comprimento de onda, como mostra a etapa a) da imagem. Para obstáculos ou orifício de dimensões muito superiores aos do comprimento de onda, os efeitos de difração ficam restritos a uma faixa estreita, nos contornos da sombra e, comumente, misturados com a região da penumbra. A b) mostra uma situação em que a propagação de uma onda segue o modelo da óptica geométrica.
Isaac Newton (1642-1727) também havia se interessado pelo fenômeno da luz, tendo realizado, no período de 1665 a 1666, surpreendentes experiências no campo da óptica, como a decomposição da luz branca através de um prisma.
Contudo, sua abordagem ao problema refletia as ideias contidas em seu trabalho sobre a gravitação, desenvolvido nesse mesmo período. Newton tinha em mente o modelo corpuscular que explicava de forma satisfatória a óptica geométrica. A possibilidade de propagação retilínea de uma onda só viria a ser formalmente demonstrada mais de um século depois, por Augustin Jean Fresnel (1788-1827).
Newton repetiu muitos dos experimentos de Grimaldi, mas deixou-os de lado quando percebeu que não podia explicar suas observações em termos do modelo corpuscular.
A disputa entre Newton, com sua teoria corpuscular que trazia à baila o modelo atômico de Demócrito, e o onipotente Robert Hook (1635-1703), que apoiava o modelo ondulatório de Huygens, não tinha como ser solucionada na época.
Se, por um lado, Newton não podia explicar as franjas de difração observadas por Grimaldi, por outro, o modelo ondulatório de Huygens não era completo o suficiente para demonstrar, de forma cabal, a propagação retilínea da luz. Nem ao menos eram conhecidos os valores aproximados dos comprimentos de onda associados ao espectro luminoso.
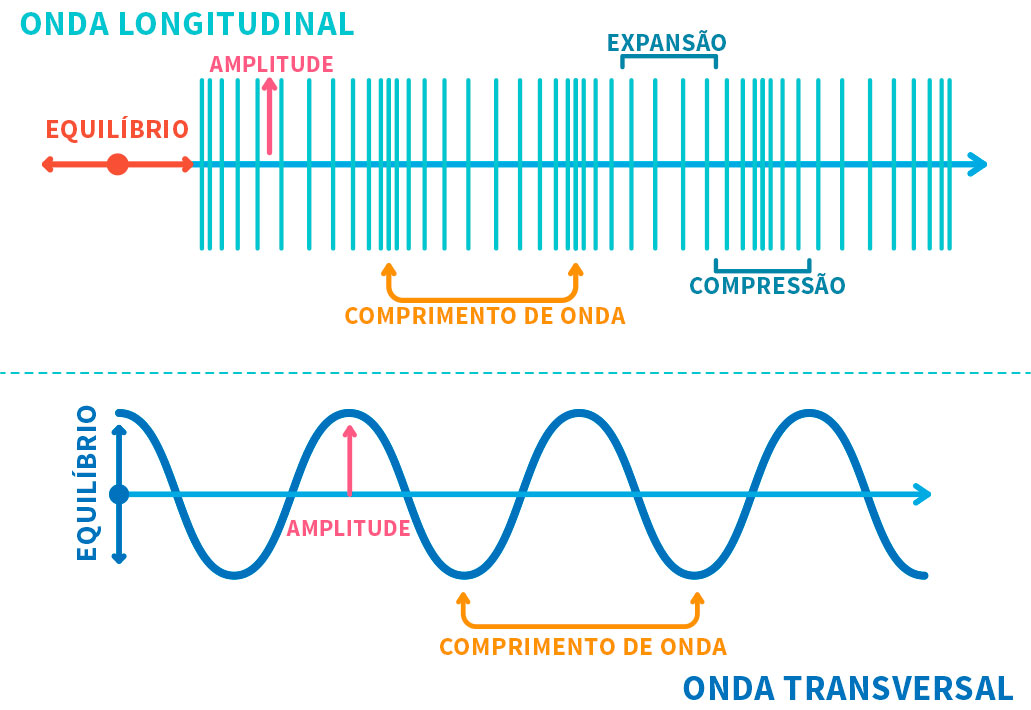
Alguns outros fenômenos também eram facilmente explicáveis pela teoria ondulatória, como a birrefringência. Na época, era difícil conceber a existência de ondas transversais, como se pode ver na primeira imagem (a), descritas por duas polarizações cruzadas e que possibilitam a existência de dois índices de refração em alguns cristais. Naquele tempo, todas as ondas eram compreendidas como sendo longitudinais, como na segunda imagem (b), tais como as ondas sonoras.
Birrefringência
Propriedade óptica de um material que possui diferentes índices de refração para diferentes direções de propagação da luz.
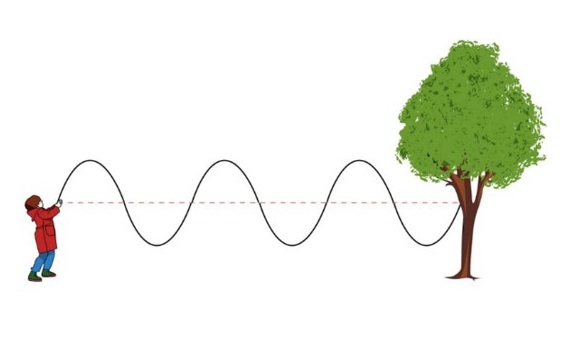
Imagem a
Ondas transversais se propagando em uma corda.
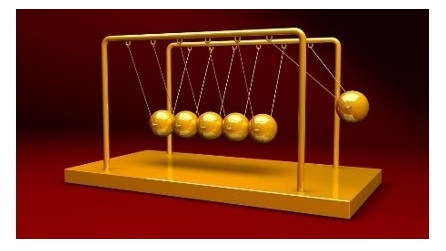
Imagem b
Ondas longitudinais, oriundas do impacto da primeira bola.
As duas teorias ofereciam, contudo, previsões antagônicas quanto à velocidade dentro da matéria.
Enquanto Newton explicava a refração pelo aumento da velocidade das partículas luminosas ao entrarem dentro de um corpo, pela ação da força gravitacional, Huygens propunha justamente o contrário.
Para se chegar a alguma conclusão sobre a natureza da luz era necessário vencer duas etapas:
Clique nos cards a seguir.
De modo que pudessem explicar corretamente os resultados experimentais.
Com a precisão necessária.
A primeira etapa tinha como obstáculo o enorme peso científico do legado de Newton. Da mesma forma que a admiração por Sócrates havia canalizado o intelecto da Antiguidade para a filosofia moral, a influência de Newton sobre as gerações seguintes fez com que poucos se atrevessem a contestá-lo nos cem anos que se seguiram à sua morte.
A segunda etapa implicava em um avanço tecnológico que propiciasse aos cientistas uma instrumentação adequada para medir a velocidade da luz. Isso só aconteceu em 1850, quando, finalmente, Jean Bernard Léon Foucault (1819-1868) mediu a velocidade da luz no ar e na água, mostrando que a velocidade na água era menor do que no ar (RICARDO B., 2005).
MEDIDA DA VELOCIDADE DA LUZ

Foi só entre o final do século XVIII e o início do século XIX que o modelo ondulatório recebeu o impulso necessário para o seu desenvolvimento. As causas para essa demora podem ser atribuídas, quase exclusivamente, a Newton.

Apesar do caminho trilhado ter requerido engenhosidade e perseverança, foi a grande pedra colocada por Newton no início – quando pôs a sua reputação científica ao lado do modelo corpuscular – que desencorajou mais de uma geração de adeptos do modelo ondulatório.

Esse atraso poderia ter sido evitado se a medida da velocidade da luz dentro e fora da matéria tivesse sido realizada antes. Entretanto, a resolução desse problema requeria avanços tecnológicos sem os quais qualquer medição se tornava impossível.
Para termos uma ideia mais clara da dificuldade de se medir a velocidade da luz, é necessário analisar algumas ordens de grandeza envolvidas.
Como sabemos atualmente, a luz se propaga no vácuo a uma velocidade de cerca de 300 mil quilômetros por segundo (em notação científica: c = 3,0 x 108m/s).
A letra c foi designada para representar a velocidade da luz no vácuo. A origem da palavra vem de celeridade (rapidez), utilizada no passado para caracterizar a velocidade de propagação de uma onda.
Comparativamente ao som, que se propaga em nossa atmosfera a uma velocidade de cerca de 340m/s, a luz se propaga quase um milhão de vezes mais rápido.
Para compreender o quanto a luz é veloz, podemos fazer a seguinte comparação:
Galileu duvidava que a velocidade da luz fosse infinita e planejou um experimento para medir essa velocidade, cobrindo e descobrindo, manualmente, lanternas separadas por duas colinas.
Embora a ideia fosse boa, como o tempo mínimo de resposta do sistema nervoso do corpo humano é de alguns décimos de segundos (~ 0,2s), e o tempo a ser medido, no trajeto da luz de uma colina a outra, era de 33 milionésimos de segundo (0,000033s), é obvio que o erro introduzido no processo era muitíssimo maior do que o valor da grandeza determinada.
A primeira medição bem-sucedida da velocidade da luz foi feita por Ole Romer (1644-1710), em 1676. Ele percebeu que, dependendo da geometria Terra-Sol-Júpiter, poderia haver uma diferença de até mil segundos entre os tempos previstos dos eclipses das luas de Júpiter e os tempos reais em que esses eclipses fossem observados.
Ele presumiu corretamente que isso se deve ao tempo variável que leva para a luz viajar de Júpiter à Terra, pois a distância entre esses dois planetas varia. Ele obteve um valor de c equivalente a 214.000km/s, que era muito aproximado, uma vez que as distâncias planetárias não eram conhecidas com precisão naquela época.
Em 1728, James Bradley (1693-1762) fez outra estimativa ao observar a aberração estelar, sendo o deslocamento aparente das estrelas devido ao movimento da Terra em torno do Sol. Ele observou uma estrela em Draco e descobriu que sua posição aparente mudou ao longo do ano. Todas as posições estelares são afetadas igualmente dessa forma. Isso distingue a aberração estelar da paralaxe, que é maior para estrelas próximas do que para estrelas distantes.
Para entender a aberração, uma analogia útil é imaginar o efeito do seu movimento no ângulo em que a chuva passa por você enquanto você corre através dela. Se você ficar parado na chuva quando não há vento, ela cai verticalmente sobre sua cabeça.
Se você correr na chuva, ela se aproxima de você em um ângulo e o atinge na frente. Bradley mediu esse ângulo para a luz das estrelas e, conhecendo a velocidade da Terra em torno do Sol, encontrou um valor para a velocidade da luz de 301.000km/s.
Depois que James Clerk Maxwell (1831-1879) publicou sua teoria do eletromagnetismo, tornou-se possível calcular a velocidade da luz indiretamente, medindo a permeabilidade magnética e a permissividade elétrica do vácuo. Isso foi feito pela primeira vez por Weber e Kohlrausch, em 1857. Em 1907, Rosa e Dorsey obtiveram 299.788km/s. Era o valor mais preciso na época.
Saiba mais
Muitos outros métodos foram, subsequentemente, empregados para melhorar ainda mais a precisão da medição de c, de modo que logo se tornou necessário corrigir o índice de refração do ar, visto que c é a velocidade da luz no vácuo.
Depois de 1970, o desenvolvimento de lasers com estabilidade espectral muito alta e relógios de césio precisos tornaram possíveis medições ainda melhores. Até então, a mudança de definição do medidor sempre esteve à frente da precisão nas medidas da velocidade da luz.
Em 1970, a velocidade da luz era conhecida por apresentar um erro de mais ou menos 1m/s. Tornou-se mais prático fixar o valor de c na definição do medidor e usar relógios atômicos e lasers para medir distâncias precisas. Atualmente, a velocidade da luz no vácuo é definida com um valor fixo e exato, quando fornecida em unidades padrão.
Desde 1983, o metro é definido por acordo internacional como a distância percorrida pela luz no vácuo durante um intervalo de tempo de 1/299.792.458 de segundo. Isso torna a velocidade da luz exatamente 299.792,458km/s. Essa definição só faz sentido porque a velocidade da luz no vácuo é medida com o mesmo valor por todos os observadores.
ONDAS ELETROMAGNÉTICAS (OEM)
Toda onda, seja uma onda elástica se propagando em meio material ou uma onda eletromagnética no vácuo, tem uma caracteristica em comum: grandezas y a elas associadas, que obedecem à equação de ondas dada por:
Equação 1
Essa onda se propaga com velocidade v na direção x. No caso de uma onda em uma corda, y representa o deslocamento vertical; e, em uma mola, o deslocamento longitudinal. No caso de ondas sonoras, y corresponde à variação de pressão e, no caso de ondas eletromagnéticas, às componentes do vetor campo elétrico E e do vetor campo magnético B.
Iniciamos considerando uma onda eletromagnética plana no vácuo, isto é, que se propaga em uma única direção x, além de ser linearmente polarizada com o campo elétrico paralelo ao eixo y e o campo magnético paralelo ao eixo z.
Diversas características dessa onda – como transporte, dissipação, geração e armazenamento de energia nos meios materiais –, podem ser descritas por meio das equações de Maxwell. Começamos escrevendo a lei de Gauss para o campo elétrico e a lei de Faraday-Henry:
Equação 2
Equação 3
E a lei de Gauss para o campo magnético e a lei de Ampère-Maxwell:
Equação 4
Equação 5
Em que μ0 ϵ0 são respectivamente a permissividade e permeabilidade do vácuo, cujos valores são:
Derivando a equação 2 em relação a x:
Equação 6
E a equação 4 em relação a t:
Equação 7
A combinação das equações 6 e 7 resulta em:
Equação 8
Que é uma equação perfeitamente similar à equação 1, indicando que o campo E se propaga ao longo do eixo x com a velocidade dada por:
Equação 9
Cujo valor pode ser calculado substituindo ϵ0e μ0, do que obtemos:
Que é exatamente a velocidade da Luz!
Uma solução da equação 8 é uma onda senoidal dada por:
Equação 10
A amplitude do campo elétrico é , a constante é chamada número de onda e a frequência angular é , dada por sendo T o período da onda, isto é, o tempo necessário para uma onda percorrer uma distância correspondente a um comprimento de onda e n é a frequência da onda, ou seja, o número de oscilações por unidade de tempo.
A unidade de frequência no sistema internacional é s-1, que recebe o nome especial de Hertz (Hz).
Por um procedimento similar podemos obter uma solução para o campo magnético, que também é uma onda senoidal:
Equação 11
Em que B0 é a amplitude do campo magnético.
Atenção
Demonstramos, assim, que as componentes do campo elétrico E e magnético B, das ondas eletromagnéticas planas, são perpendiculares entre si e também à direção de propagação e que sua velocidade de propagação é a mesma da luz.
Derivando a equação 10 em relação à x e a 11 em relação à t, obtemos:
Equação 12
Equação 13
Essas duas equações se igualam, conforme a equação 2. Obtém-se, então:
Equação 14
Usando 10, 11 e 14, obtemos:
Equação 15
Atenção
Isto é, em qualquer instante, a razão entre E e B é igual a c.
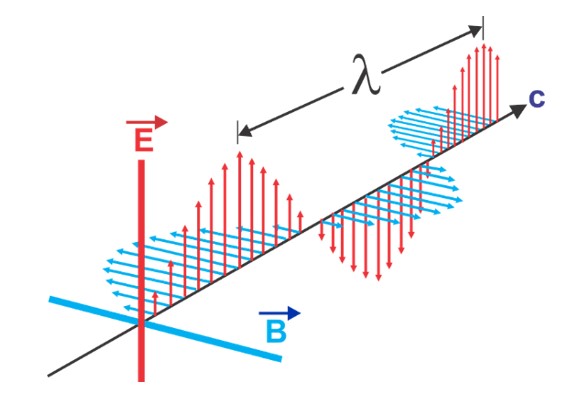
Podemos concluir que esses campos estão em fase, alcançando os valores zero e máximo, denominada amplitude, ao mesmo tempo. Os campos negativos significam que houve mudança no sentido dos campos. Uma onda eletromagnética plana linearmente polarizada está representada na imagem ao lado.
Uma característica importante de qualquer onda é a capacidade de transportar energia sem necessariamente transportar massa ou matéria. Uma onda eletromagnética, como qualquer outra onda, transporta energia ao se propagar e, quando encontra objetos, pode transferir energia a eles.
ESPECTRO ELETROMAGNÉTICO
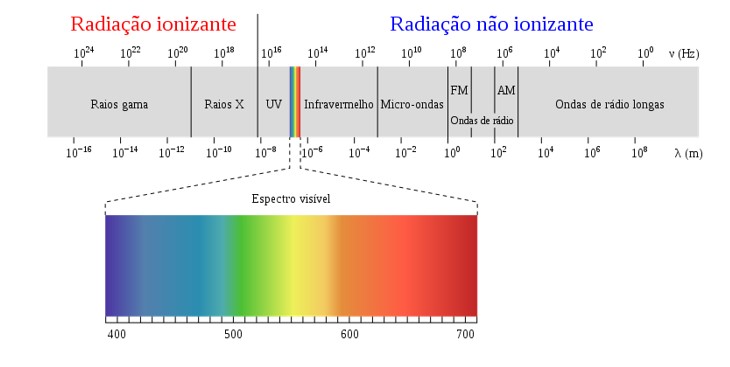
O espectro eletromagnético é constituído por ondas eletromagnéticas com comprimentos de onda que variam em uma faixa extremamente ampla. As várias faixas de comprimento de onda ou frequência desse espectro receberam denominações especiais. A separação entre as faixas não é muito rigorosa, podendo se sobrepor, uma vez que ela foi feita mais por motivos históricos do que propriamente físicos ou biológicos.
A radiação infravermelha foi a primeira a ser descoberta, em 1880, depois da luz. A seguir, foram descobertas a radiação ultravioleta, em 1881; as ondas de rádio, em 1888; a radiação X, em 1895; a radiação gama, em 1900; e as micro-ondas, em 1932.
A caracterização das ondas eletromagnéticas na região de frequência baixa que corresponde desde 0Hz até o início da radiação infravermelha é comumente feita em termos de frequência. Assim, diz-se que as ondas curtas de 27,12MHz, por exemplo, são usadas para aquecer partes do corpo em fisioterapia, e as micro-ondas, com frequência de 2450MHz, para cozinhar e aquecer alimentos.
A região que contém a radiação conhecida como óptica, composta por radiação infravermelha (IV), luz visível e raios ultravioleta (UV), é usualmente caracterizada pelo comprimento de onda. A luz, comumente designada luz visível, compreende a faixa de 400nm (luz roxa) a 700nm (luz vermelha).
A unidade nanômetro, abreviada nm, é usada para pequenos comprimentos: 1nm = 10-9m. A radiação ultravioleta é também comumente designada luz ultravioleta.
Finalmente, a faixa que compreende os raios X e os raios gama é especificada pela energia do fóton. Dizemos que os raios X usados na mamografia, por exemplo, têm energia média de 30keV e a energia da radiação gama emitida pelo Césio-137 é de 0,66MeV. Na verdade, essas são as energias de cada fóton, de cada feixe.
Fóton
Substantivo que representa uma unidade de radiação de um feixe.
Você sabia
Elétron-volt (eV) é uma unidade de energia que não pertence ao sistema internacional e é usada para energias extremamente pequenas. Corresponde à energia adquirida por um elétron quando ele é acelerado no vácuo por uma diferença de potencial de 1 Volt (V).
A imagem a seguir mostra o espectro eletromagnético em várias faixas, sendo a principal entre radiação ionizante e não ionizante.
A NATUREZA ONDULATÓRIA DA LUZ
Para sintetizar, o vídeo a seguir apresentará uma descrição cronológica sobre natureza ondulatória da luz, bem como explicará o que é uma onda eletromagnética e seu espectro.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Identificar a natureza da luz na visão contemporânea e seu comportamento ondulatório e/ou corpuscular (dualidade onda-partícula)
NATUREZA QUÂNTICA DA LUZ
À primeira vista, a natureza quântica da luz pode ser um conceito estranho e desconcertante. A luz agindo como pedaços discretos, partículas sem massa fornecendo momentos e partículas fundamentais se comportando como ondas, muitas vezes, podem parecer algo saído do livro Alice no País das Maravilhas.
Para muitos, o estudo desse ramo da Física pode ser tão fascinante quanto um romance clássico, um filme ou ainda uma série de sua preferência. Relembrando as obras de personagens lendários e cientistas brilhantes como Einstein, Planck e Compton, o estudo da natureza quântica da luz fornecerá a você um conto interessante de como uma interpretação inteligente de alguns detalhes levou às descobertas mais importantes dos últimos 150 anos.
Você sabia
Da revolução eletrônica do século XX ao nosso progresso futuro na energia solar e na exploração do espaço, a natureza quântica da luz deve produzir curiosas consequências, nas quais residem algumas das verdades mais fascinantes de nosso tempo.
RADIAÇÃO TÉRMICA
Um trabalho apresentado por Max Karl Ludwig Planck, em 14 de dezembro de 1900, com o título Sobre a teoria da Lei da distribuição de Energia do espectro Normal, mostrou falhas importantes na teoria clássica da Termodinâmica. Essa data marcou o início de mais uma revolução na Física. Surgiu, então, a teoria quântica.
A seguir, os detalhes da teoria de Planck e sua importância para a origem da teoria quântica moderna.
RADIAÇÃO DE CAVIDADE E CORPO NEGRO
Um corpo negro, como seu próprio nome indica, é um sólido que absorve toda a radiação que incide sobre sua superfície, a radiação térmica. Tal dispositivo se refere a uma cavidade construída no interior de um sólido qualquer, aquecido a uma temperatura T, que se comunica com o meio externo através de um pequeno orifício, como mostram as imagens.
Exemplo de absorção térmica em uma cavidade construída no interior de um sólido com pequeno orifício (corpo negro)
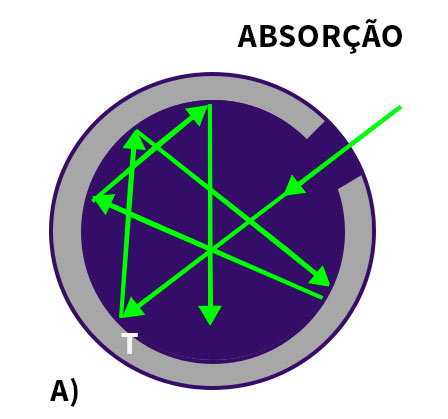
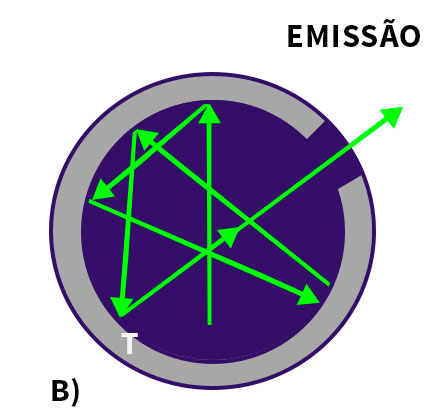
Em geral, a radiação térmica tem uma distribuição espectral contínua de frequências. As radiações térmicas são ondas eletromagnéticas geradas pelas oscilações das partículas carregadas que compõem os sólidos aquecidos.
Em baixas temperaturas, um sólido pode ser visto, não por emissão, mas por reflexão da luz. Entretanto, em altas temperaturas, os sólidos podem emitir luz visível, embora mais de 90% estejam na região do infravermelho do espectro eletromagnético. Carvão em brasas, filamento aquecido de uma lâmpada e estrelas são exemplos de sólidos aquecidos que irradiam no visível.
Assim, um corpo negro ideal não reflete nada, mas, ao absorver toda a radiação incidente, um corpo negro se aquece. Isso significa que toda a energia interna do corpo é distribuída termicamente, o que envolve uma distribuição de energias definida pelas leis da termodinâmica, dependendo apenas da temperatura absoluta.
Essa distribuição térmica de energias pode ser investigada por meio do espectro de emissão do corpo negro.
Note que um corpo negro pode emitir luz, só não pode refleti-la em sua superfície.
A imagem a seguir apresenta alguns exemplos de distribuições espectrais para diferentes temperaturas em Kelvin (K) de um corpo negro. Somente a partir de uma temperatura em torno de 800K é que começa a haver emissão na região visível do espectro eletromagnético. Nessa temperatura, o corpo se incandesce e tem uma cor vermelho-rubro.
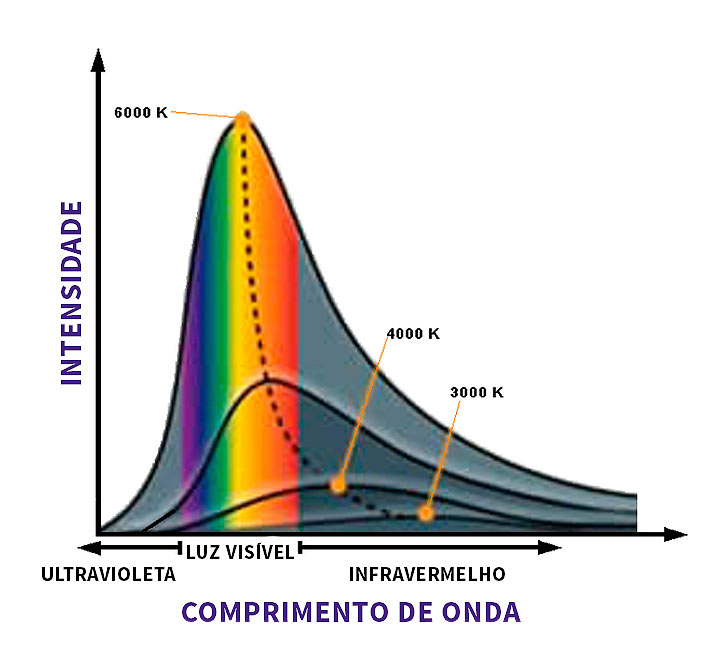
Por causa da habilidade de absorver toda a radiação vinda do meio externo, o orifício da cavidade tem características de um corpo negro e a radiação térmica emitida por ele é conhecida como radiação de corpo negro.
Praticamente, toda a radiação vinda do meio externo, que entra na cavidade através do orifício não consegue sair dela, e será refletida um certo número de vezes até ser absorvida pelas paredes internas, como vimos na imagem anterior. Com a agitação térmica, as partículas carregadas que compõem as paredes da cavidade oscilam e produzem radiação térmica, que é emitida através do orifício.
Absorção
Uma radiação que penetre na cavidade (absorção), como no exemplo (a), através de um pequeno orifício de comunicação com o meio externo, entrará em equilíbrio térmico com o seu interior.
Emissão
A energia que entrou só poderá escapar (emissão) pelo mesmo orifício de comunicação com o meio externo, como no exemplo (b), após ser moldada pela curva espectral de radiância definida pela condição termodinâmica de temperatura T do seu interior. O orifício na cavidade, portanto, assume o papel de um corpo negro. Qualquer radiação que incida no orifício será absorvida e a radiação emitida será característica da distribuição térmica interna à cavidade.
A intensidade de radiação em função do comprimento de onda a uma dada temperatura é chamada de radiância espectral. No final do século XIX, já havia dados experimentais da distribuição espectral da radiação de um corpo negro. Gustav Kirchhoff (1824-1887), em 1859, provou que a radiação emitida (RT) depende apenas da temperatura absoluta T e do comprimento de onda , da seguinte forma:
A intensidade de radiação de um corpo negro aumentava com a temperatura.
A radiação era função do comprimento de onda emitido.
O comprimento de onda para o qual a radiância espectral é máxima é uma função inversa da temperatura.
Ele lançou, então, um desafio aos físicos para que encontrassem uma função RT ().
Em 1879, Josef Stefan (1835-1893), usando argumentos empíricos, demonstrados teoricamente mais tarde, em 1884, por Ludwig Eduard Boltzmann, lei que ficou conhecida como lei de Stefan-Boltzmann, mostra que energia total emitida (E) por um corpo negro seria proporcional à quarta potência da temperatura absoluta , demonstração matemática a partir da termodinâmica e da teoria eletromagnética de Maxwell, sendo escrita na forma:
Em que é uma constante universal denominada de constante de Stefan-Boltzman. Contudo, a função RT() ainda não havia sido encontrada.
Em 1896, Wilhelm Carl Werner Otto Fritz Franz Wien (1864-1928) propôs uma solução para o desafio de Kirchhoff na forma:
Em que C1 e C2 são constantes. Embora essa função se ajustasse a valores experimentais na faixa de pequenos comprimentos de onda, ela se desviava na região do infravermelho, como mostraram Heinrich Rubens (1865-1922) e Ferdinand Kurlbaum (1857-1927), em 1898; e Otto Richard Lummer (1860-1925) e Ernest Pringsheim (1859-1917), em 1899, com medidas mais precisas da radiância espectral.
Teoria de Rayleigh-Jeans para a radiação de corpo negro
No início de século XX, John William Strutt (1842-1919) e James Hopwood Jeans (1877-1946), utilizando a teoria clássica para estudar a densidade de energia da radiação de cavidade, ou de corpo negro, o que resultou em sérias inconsistências com os dados experimentais, publicaram um artigo propondo uma modificação na lei de Wien.
Saiba mais
No lugar da dependência com , eles sugeriram uma dependência com , de maneira que a curva se ajustasse aos valores experimentais na região do infravermelho. Essa função, apesar de descrever bem a região de grandes comprimentos de onda, falhava na região de comprimentos de ondas pequenos, como a ultravioleta. Como não era sustentada com um modelo teórico, foi dada pouca atenção a ela.
Teoria de Planck
Rubens visitou Max Karl Ernest Ludwig Planck (1858-1947) em outubro de 1900, e explicou seus resultados. Poucas horas depois de Rubens ter deixado a casa de Planck, este imaginou uma fórmula para a função RT () de Kirchhoff. Essa fórmula desenvolvida empiricamente se ajustava muito bem a todos os comprimentos de onda, mas Planck não estava satisfeito. Ele queria desenvolver a fórmula teoricamente.
O problema com que Planck se deparou e que Jeans descreveria detalhadamente mais tarde, em 1905, em um artigo, estava no que ficou conhecido como a “Catástrofe Ultravioleta”, conforme imagem:
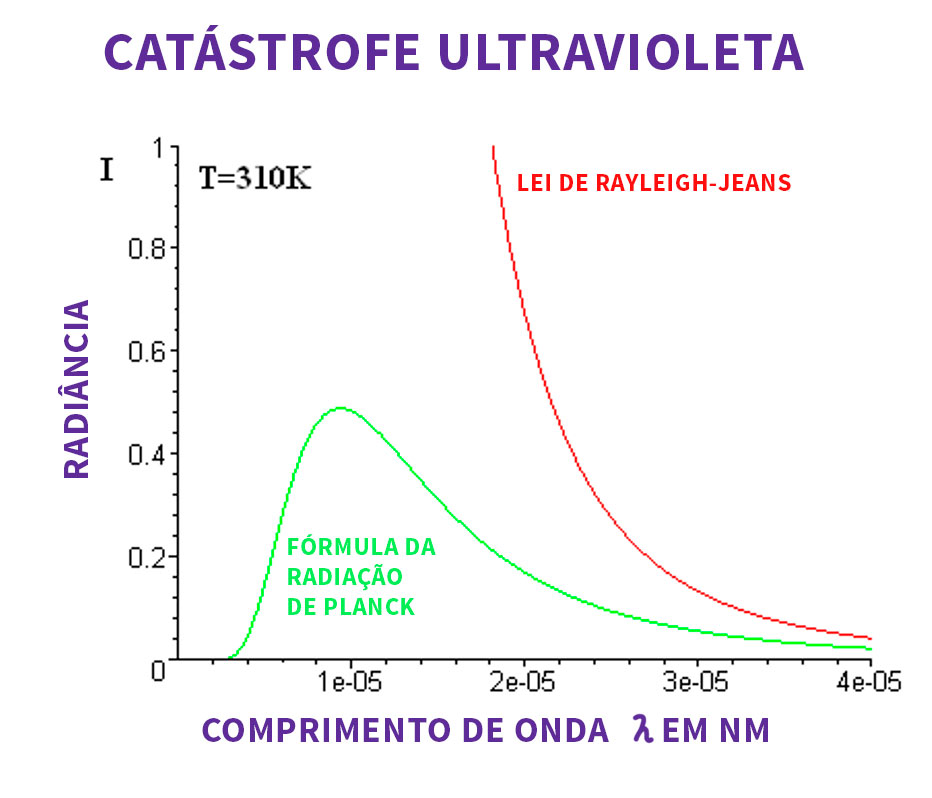
A teoria clássica, para o cálculo da distribuição espectral de energias dentro do corpo negro, descreveria perfeitamente o comportamento para grandes comprimentos de onda. Contudo, para na faixa do ultravioleta, ela divergia profundamente. Esse resultado clássico é descrito pela função:
Denominada como lei de Rayleigh-Jeans.
Ao longo de muitos anos, vários físicos tentaram conciliar o conceito de corpo negro com a distribuição de energia prevista pela termodinâmica. No entanto, nenhum resultado previsto pela teoria era compatível com os espectros obtidos experimentalmente com sistemas que simulavam um corpo negro.
Em 1901, Max Planck, ao reinterpretar a emissão à radiação, na tentativa de solucionar a inconsistência entre a teoria clássica e a experiência para a radiação de cavidade, teve que assumir uma hipótese que violava o princípio da equipartição de energia. Planck percebeu que o resultado experimental seria reproduzido, quando: A energia total média tende a kT (), como na teoria clássica, quando a frequência tende a zero, mas tende a zero quando a frequência tende ao infinito.
Assim, Planck supôs que a energia média dos modos eletromagnéticos é uma função da frequência , contrariando o princípio da equipartição de energia.
O princípio da equipartição de energia tem sua origem na distribuição de partículas clássicas de Boltzmann. Em equilíbrio térmico a uma temperatura T, a energia é compartilhada igualmente entre todas as suas várias formas. Por exemplo, a energia cinética média por grau de liberdade no movimento translacional de uma molécula deve ser igual à do movimento rotacional.
Para isso, é necessário primeiro calcular a densidade de modos de uma frequência (número de modos por unidade de frequência) e depois multiplicar pela densidade de energia média dessa frequência. A primeira etapa envolve apenas um estudo geométrico da cavidade e não havia o que alterar. Restava apenas, então, obter o valor para a densidade de energia média por frequência.
O cálculo clássico da energia média resultava em:
Em que
Esse valor para a energia média conduz a um perfeito ajuste com os dados experimentais na região de grandes comprimentos de onda, isto é, quando a frequência tende a zero. Para a região em que a frequência cresce, tipicamente no ultravioleta, aparece uma discrepância enorme, pois, como mostra a imagem da catástrofe ultravioleta, a curva tende a zero quando tende a zero, enquanto o resultado clássico vai a infinito.
A grande contribuição de Planck se deu quando ele observou que, em vez de assumir valores contínuos, a energia E deveria assumir somente valores discretos (pacotes de energia) e múltiplos de uma grandeza proporcional à frequência, isto é:
Em que n = 0, 1, 2, 3,...., é a frequência e h uma constante que ficou conhecida como constante de Planck e cujo valor é, atualmente:
Ao postular a quantização de energia das ondas, Planck conseguiu explicar o espectro observado experimentalmente e descrevê-lo teoricamente.
Você sabia
Por mais estranha que possa ser, a hipótese de Planck foi confirmada pela própria natureza. Para Planck, o fato de ter descrito a energia da radiação em forma de pacotes de era apenas um artificio matemático. Foi uma hipótese revolucionária. Planck recebeu o prêmio Nobel de Física em 1918 por esse trabalho.
Não havia nenhuma evidência direta de que a luz era composta de quantidades, ou quanta, discretas de energia. Eis o nascimento da Física quântica.

Em termodinâmica, o princípio do corpo negro é usado para determinar a natureza e a quantidade de energia emitida por um corpo aquecido. A radiação do corpo negro tem servido como uma importante fonte de confirmação para a teoria do Big Bang, a qual assegura que o universo nasceu em uma explosão monumental ocorrida cerca de aproximadamente 13,8 bilhões de anos atrás.
De acordo com a teoria, a explosão deixou uma radiação de fundo cósmica do corpo negro remanescente que é uniforme em todas as direções e tem uma temperatura equivalente a somente uns poucos graus kelvin. Essa radiação uniforme, com temperatura de 2,7K, foi descoberta em 1964 por Arno A. Penzias (1933) e Robert W. Wilson (1936), os quais receberam o prêmio Nobel de Física em 1978 por seu trabalho.
Dados recentes obtidos pelo satélite COBE (Cosmic Microwave Background Explorer) da NASA, tem revelado pequenas flutuações na radiação que estão sendo interpretadas como relacionadas às “sementes” de estrelas e galáxias.
Postulados de De Broglie
Em sua tese de doutorado, apresentada em 1924 à Faculdade de Ciências da Universidade de Paris, Louis Victor Pierre Raymond, 7º duque de Broglie, postulou a existência da onda de matéria. De Broglie propôs que os elétrons também se comportariam como ondas. Seu argumento foi: já que a luz se comporta ora como onda, ora como matéria, por que a matéria não poderia fazer o mesmo?
Baseado na teoria dos quanta de energia, proposta por Planck e Einstein, o trabalho de De Broglie constituiu uma das principais bases da mecânica quântica. Cinco anos mais tarde, De Broglie recebeu o prêmio Nobel de Física, quando suas ideias foram definitivamente comprovadas por experiências. Foi a ideia da onda de matéria de De Broglie que inspirou Erwin Schrödinger a propor a sua teoria quântica moderna.
Para De Broglie, a dualidade onda-partícula da radiação também deveria ocorrer com a matéria. Para isso, ele considerou a questão mais simples possível, isto é, um corpúsculo em movimento retilíneo e uniforme, com energia e momento conhecidos.
De acordo com essa hipótese, a energia E = hn e o comprimento de onda , associado ao momento linear de módulo p, pode ser descrito por:
É conhecida como equação de De Broglie e prevê um comprimento de onda de De Broglie para uma partícula em movimento com momento linear de módulo p.
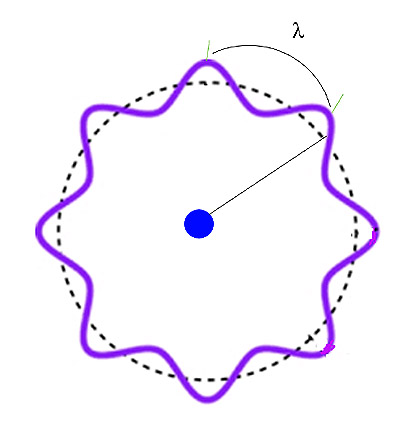
A quantização do momento angular no átomo, proposta empiricamente por Bohr, pode ser obtida diretamente do postulado de De Broglie. Como o elétron no átomo deve mover-se em órbitas discretas e fechadas, de acordo com o postulado de Bohr, então, uma órbita de raio r deve conter um número inteiro n de onda de De Broglie do elétron, como mostra a imagem ao lado.
De acordo com essa ideia, a razão entre o perímetro da orbita e o comprimento de onda de De Broglie, resulta em um número inteiro n dado por:
em que é o momento angular clássico do elétron e .
Sabe-se que, no caso da luz, o limite de utilização da óptica geométrica ocorre para comprimentos de onda () muito menores do que a dimensão da abertura, ou obstáculos. Assim, no domínio da óptica geométrica, a luz se comporta como raios geométricos, similarmente ao caso das trajetórias das partículas clássicas macroscópicas.
Entretanto, quando o comprimento de onda () é muito maior do que a dimensão de abertura, o ângulo de difração torna-se importante, a natureza ondulatória da luz se evidencia e o fenômeno deve ser descrito pela óptica ondulatória.
Para se observar a natureza ondulatória da matéria são necessárias aberturas, ou obstáculos, convenientemente pequenas.
Na época de De Broglie, os sistemas mais apropriados para esse fim eram os espaçamentos entre planos adjacentes de um cristal, de aproximadamente 1A° (Angstron = 10-10 metros). Atualmente, tem-se acesso a sistemas que envolvem dimensões nucleares cujas dimensões de abertura são de aproximadamente 10-4A°. Ao considerar o comprimento de De Broglie, vê-se que não se pode esperar a detecção de qualquer evidência de movimento ondulatório no movimento da bola de boliche, em que o ângulo de difração é (θ) ≈ 10-25A° , para uma abertura de aproximadamente 1A°.
Em 1927, Clinton Joseph Davisson (1881-1958) e Lester Halbert Germer (1896-1971), demonstraram, experimentalmente, pela primeira vez, a difração de elétrons através de cristais. Essa experiência, por incrível que pareça, comprovou a hipótese da natureza ondulatória do elétron. A experiência de Davison e Germer, como é chamada, é mostrada nas imagens a seguir.
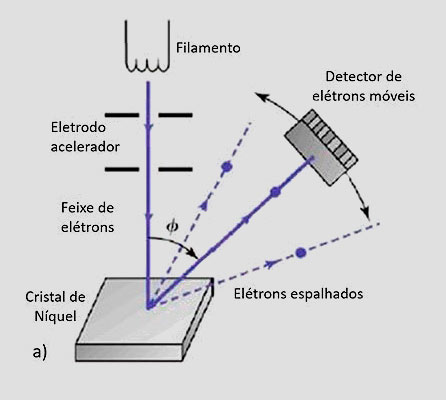
Experimento de Davisson e Germer.
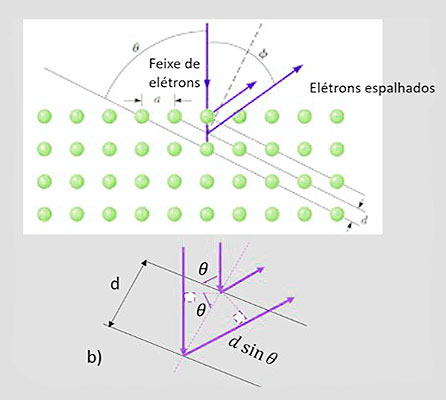
Experimento de Davisson e Germer.
No experimento, um feixe de elétrons de baixa energia é produzido em um filamento aquecido e acelerado por uma diferença de potencial V. O feixe eletrônico incide normalmente sobre a superfície de um cristal de Níquel. Um detector é colocado a um ângulo em relação ao feixe incidente para medir a intensidade do feixe espalhado.
Na experiência, espera-se encontrar regiões de máximos e mínimos de intensidade, resultantes das interferências construtiva e destrutiva nos planos cristalinos do cristal de Níquel. Exatamente como ocorre com o espalhamento de raios X nos cristais, para incidência normal, a condição de interferência construtiva, ou na linguagem cristalográfica “a condição de Bragg”, fornece:
A experiência mostra que existe uma intensidade máxima para b=50° ou α = 65°, obtidas da experiência, encontra-se o comprimento de onda do feixe espalhado como:
Por outro lado, o comprimento de onda de De Broglie para elétrons de energia cinética K = 54 eV = 86,4 x 10-19 J: será:
A concordância entre os resultados confirma quantitativamente a hipótese da onda de matéria de De Broglie.
Ainda em 1927, George Paget Thomson, filho de J. J. Thomson, mostrou a difração de feixes de elétrons ao passar através de películas cristalinas, confirmando, de forma independente, o postulado de De Broglie.
A imagem mostra uma ilustração de difração do espalhamento de elétrons numa película de cristal de ouro. O resultado é similar ao espalhamento de raios X em cristais, em que o fenômeno da difração aparece por causa de aberturas circulares no interior do filme cristalino.
É interessante mencionar que Joseph John Thomson recebeu o prêmio Nobel de Física, em 1906, pela medida da razão carga/massa do elétron, enquanto seu filho, George Paget Thomson, recebeu o prêmio Nobel de Física, em 1937, por experimentos de difração com elétrons, realizados em 1927.
Saiba mais
Pode-se dizer que Thomson, o pai, recebeu o prêmio Nobel por ter mostrado que o elétron é uma partícula, e Thomson, o filho, recebeu o prêmio Nobel por ter mostrado que o elétron é uma onda.
Interpretação probabilística da dualidade onda-partícula
Sabe-se, agora, que a dualidade onda-partícula se aplica tanto à radiação quanto à matéria. Em alguns casos, é necessário recorrer ao modelo corpuscular e, em outros, ao modelo ondulatório. Entretanto, é importante mencionar que os dois aspectos não se revelam simultaneamente em um mesmo experimento.
Quando a radiação, ou matéria, é detectada por interação, de modo a ser localizada, ela se comporta como partícula. Por outro lado, quando ela se move no espaço livre, de modo a ser deslocalizada, comporta-se como uma onda, e fenômenos de difração são observados.
Nils Bohr resumiu a questão em seu princípio da complementaridade: “O modelo corpuscular e o ondulatório são complementares e não contraditórios”: a experiência que comprova o caráter ondulatório da radiação é incapaz de comprovar o caráter corpuscular e vice-versa.
Para identificar o caráter ondulatório e corpuscular em um só experimento, é necessário incorporar uma interpretação probabilística à dualidade onda-partícula.
A interpretação probabilística da dualidade onda-partícula, para o caso da radiação, foi proposta por Albert Einstein. Em seguida, Max Born usou argumentos similares para o caso da matéria. No modelo ondulatório, a intensidade (I) da radiação é proporcional ao quadrado do módulo do campo elétrico (E), isto é:
No modelo corpuscular, ou de fótons, a intensidade da radiação é dada em função da frequência (), isto é:
Assim, nas diferentes interpretações, ondulatória e corpuscular, para a intensidade da radiação, espera-se que, nas regiões em que o campo elétrico é mais intenso, a concentração de fótons seja maior.
O próprio conceito de fóton, proposto por Einstein para descrever a radiação eletromagnética, implica uma interpretação probabilística para a intensidade luminosa. Tal fato pode ser observado na experiência de interferência de dupla fenda de Young, mostrada a seguir.
Experimento de dupla fenda de Young
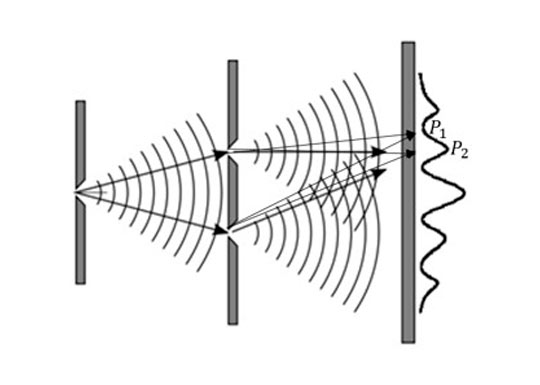

O padrão de interferência observado no anteparo é resultante da interferência entre as ondas provenientes das duas fendas. No ponto P1, onde a interferência é destrutiva, o campo elétrico resultante é nulo e nenhum fóton é observado. No ponto P2, onde a interferência é construtiva, o campo elétrico resultante é máximo e muitos fótons são observados.
Se a intensidade da luz nas fendas for reduzida, observa-se ainda o padrão de interferência, desde que se substitua o anteparo por um filme fotográfico e espere-se um tempo suficientemente longo para sensibilizá-lo.
A interação da luz com o filme fotográfico é um fenômeno quântico. Se o filme é exposto durante um curto intervalo de tempo, com uma fonte de luz de baixa intensidade, não se observa somente uma versão menos intensa da figura de interferência obtida com luz intensa, mas também “pontos” resultantes das interações dos fótons com os cristalitos do filme, como mostrarão as imagens, em seguida.
- Nas regiões onde as ondas interferem destrutivamente, não aparecem quaisquer pontos, ou seja, existe uma probabilidade nula de que fótons atinjam essas regiões.
- Nas regiões onde a interferência é construtiva, aparecem vários pontos, indicando que é grande a probabilidade de que os fótons ali cheguem.
- À medida que a intensidade ou o tempo de exposição aumentam, as flutuações se uniformizam e não se observa mais a natureza da luz.
Figuras de interferência para diferentes intensidades, ou número de fótons, da luz que incide na dupla fenda de Young
Como o quadrado do módulo do campo elétrico é proporcional à quantidade de fótons em uma determinada área por tempo, pode-se concluir que é proporcional à probabilidade P de um fóton atingir um determinado ponto do filme.
Nos pontos onde é nulo, não se observa fótons no filme ou no anteparo, enquanto nos pontos onde o é grande, será maior a probabilidade de se observar os fótons.
Baseado nas conclusões de Einstein para a radiação, Max Born propôs uma interpretação probabilística da dualidade onda-partícula para a matéria.
Na teoria ondulatória da matéria, o movimento da partícula é descrito por uma função de onda , com dependência espacial e temporal . Do mesmo modo que o campo elétrico é uma solução da equação de onda para a radiação eletromagnética, a função de onda deve ser solução de uma equação de onda apropriada. Tal equação foi obtida por Erwin Schrödinger.
Saiba mais
A unificação da dualidade onda-partícula por Born surgiu alguns anos após Schrödinger propor o formalismo geral da mecânica quântica, baseada no postulado de De Broglie. A grande contribuição de Born se deve pela interpretação da função de onda.
A NATUREZA CORPUSCULAR DA RADIAÇÃO
Agora, com o auxílio da especialista Nilséia A. Barbosa, saiba um pouco mais a respeito da interpretação corpuscular sobre a natureza da luz e o nascimento da mecânica quântica.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Reconhecer a produção dos raios X e a importância de suas aplicações em diversas áreas.
RAIOS X

Desde 1850, pesquisa com descargas elétricas por meio de gases rarefeitos era um tópico concorrido. Tubos de raios catódicos, também conhecidos como “tubo de descarga em gases” (como os desenvolvidos por Geissler, na Alemanha, e por Crookes, na Inglaterra), eram equipamentos presentes em muitos laboratórios de Física em universidades da Europa.

O laboratório de Wilhelm Conrad Röentgen também incluía alguns desses tubos para pesquisas, e foi trabalhando com um desses tubos, que, em 8 de novembro de 1895, Röentgen anunciaria a descoberta de “um novo tipo de raio”. E tudo mudaria.

Escurecendo o laboratório e usando um tubo de raios catódicos submetido a uma alta tensão produzida por uma bobina de Ruhmkorff, Röentgen notou, a 2m do tubo, que um cartão com sal de bário apresentava fluorescência. Ele envolveu o tubo com um cartão preto, ligou e desligou a alta tensão, mas a fluorescência continuou.

Bobina de Ruhmkorff.

Bobina de Ruhmkorff.
Röentgen ficou tão intrigado com o fenômeno que passou as setes semanas seguintes trabalhando sozinho no laboratório, investigando as características do fenômeno e o poder de penetração daqueles raios para confirmar que aqueles eram, de fato, raios “novos”. Pesquisando, verificou que a nova radiação provinha do ponto em que os raios catódicos atingiam a parede de vidro do tubo, e tinha uma notável capacidade de atravessar diferentes materiais, sendo mais ou menos absorvida conforme a densidade e o peso atômico do meio penetrado.
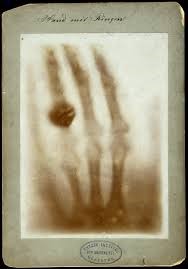
Em 22 de dezembro de 1895, Röentgen chamou sua esposa Anna Bertha para falar de sua descoberta e a convenceu a radiografar sua mão. Para isso, ela deveria manter a mão estática entre o tubo e a placa fotográfica durante 15 minutos de exposição. Hoje, as radiografias são produzidas em fração de segundo.
Após o Natal, Röentgen terminou de escrever um artigo científico sobre sua descoberta, batizando-a de Raios X, e o enviou para ser publicado em um jornal científico de Würtzburg. O artigo, contendo as primeiras radiografias produzidas, incluindo a da mão de sua esposa, foi publicado em 28 de dezembro de 1895.
No início do ano seguinte, Röentgen enviou cópias do artigo a alguns cientistas renomados. O físico Franz Exner, em um jantar informal, exibiu o artigo e todos os presentes ficaram perplexos com as radiografias. Um jornalista austríaco presente enviou as imagens para o jornal, que, no dia 5 de janeiro de 1896, publicou a notícia, na primeira página: A nova forma fantástica de ver o interior do corpo sem necessitar cortá-lo.
No dia seguinte, a notícia seria publicada na Inglaterra, no London Cronicle e, em 23 de janeiro, na revista Nature; logo após, na Science, nos EUA. Um ano após a descoberta, 49 livros e mais de mil artigos científicos tinham sido escritos sobre o assunto.
Nesse período, Röentgen descobriu várias outras propriedades dos raios X:
- Há corpos mais ou menos opacos aos raios X (por isso, as imagens radiográficas em diferentes tons de cinza);
- Não são desviados por campos elétricos ou magnéticos;
- Propagam-se em linha reta;
- Têm um alto poder de penetração;
- Produzem fluorescência em muitas substâncias: fósforo, compostos de cálcio, vidro de urânio, sal-rocha;
- Filmes fotográficos são escurecidos pelos raios X;
- Descarregam eletroscópios carregados.
Você sabia
Röentgen, mesmo sem identificar a natureza dos raios X, recebeu vários prêmios, incluindo o prêmio Nobel de Física, em 1901.
Produção de raios X
Os raios X são radiações eletromagnéticas de comprimento de onda menor do que um angstrom e com frequência acima de . Eles podem ser produzidos quando um feixe de elétrons de alta energia é acelerado por um campo elétrico intenso e colide com um alvo de átomos pesados. A imagem mostra o esquema básico de um equipamento de raios X.
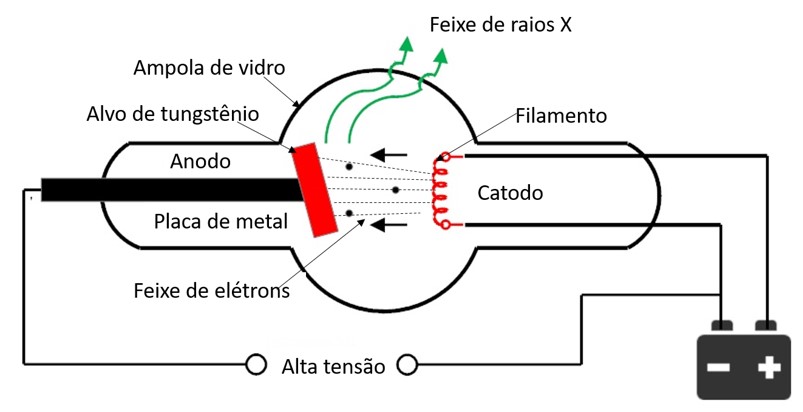

O tubo de vidro é evacuado até uma pressão de ar de cerca de 100Pa; lembre-se de que a pressão atmosférica é de 106Pa. O ânodo é um alvo metálico espesso, feito para dissipar rapidamente a energia térmica que resulta do bombardeio com os raios catódicos.

Uma alta tensão, entre 30 a 150kV, é aplicada entre os eletrodos, induzindo uma ionização do ar residual e, portanto, um feixe de elétrons do cátodo para o ânodo se inicia. Quando esses elétrons atingem o alvo, eles são desacelerados, produzindo os raios X.

O campo elétrico é obtido aplicando-se uma alta voltagem entre os terminais do tubo de raios X, em que o alvo metálico (anodo) é polarizado positivamente, e o filamento (catodo), negativamente. Quanto maior a tensão aplicada ao tubo, maior será a energia dos raios X gerados e maior também o seu poder de penetração. Aumentando-se a corrente, aumenta-se a intensidade do feixe.

Diferentemente da radiação gama e das radiações corpusculares (alfa, beta, nêutrons etc.), que são geradas nos núcleos atômicos e que podem ser obtidas naturalmente por decaimento radioativo de radionuclídeos, os raios X são provenientes da camada eletrônica dos átomos e são, em geral, obtidos por meio de tubos que promovem a produção da radiação X.
Espectro contínuo dos raios X (frenamento)
Quando os elétrons acelerados (raios catódicos) atingem o alvo de metal, eles colidem com elétrons no alvo. Em tal colisão, parte do momento do elétron incidente é transferido para o átomo do material alvo, perdendo parte de sua energia cinética, K; eles mudam de direção e alguns emitem a diferença de energia sob a forma de ondas eletromagnéticas, os raios X.
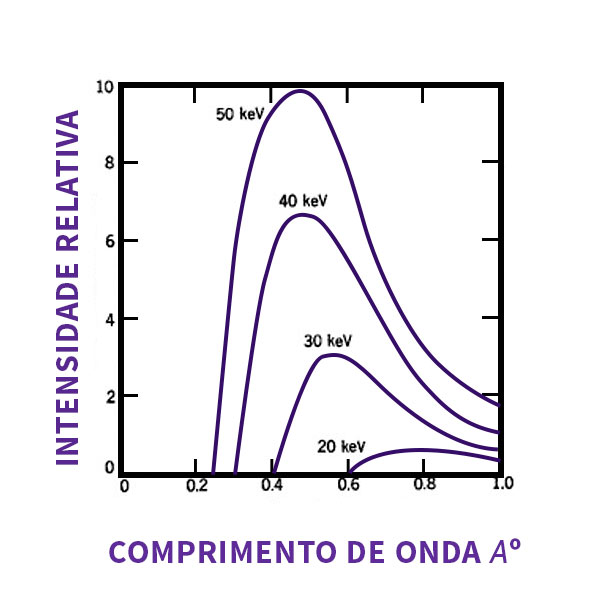
De acordo com a teoria eletromagnética clássica, a desaceleração dos elétrons causaria emissão de um espectro contínuo de radiação, desde comprimentos de onda zero até infinito. Entretanto, o espectro de raios X, para o caso de um alvo de tungstênio, para diferentes voltagens de aceleração, não está totalmente de acordo com a previsão clássica. A característica mais importante observada nos espectros é que, para uma dada energia dos elétrons, existe um comprimento de onda mínimo muito bem definido.
A intensidade varia suavemente com o comprimento de onda. A intensidade atinge um valor máximo conforme o comprimento de onda aumenta, então, cai em comprimentos de onda maiores. Para qualquer material, existe um comprimento de onda mínimo que dependerá somente da diferença de potencial V. Quanto maior a diferença de potencial, menor o valor do comprimento de onda mínimo.
Esse é o fato que a teoria eletromagnética clássica não pode explicar, pois, de acordo com essa teoria, o espectro emitido deveria ser contínuo, não havendo razão para a existência de um limiar de comprimento de onda. Se, entretanto, o modelo de fótons for adotado para os raios X, então, o fenômeno terá uma explicação satisfatória, como se verifica na sequência.
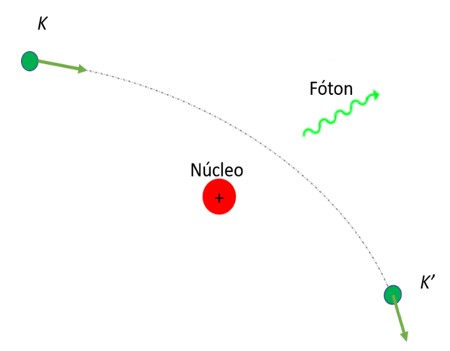
Um elétron de energia cinética K é desacelerado na interação com o núcleo pesado do átomo. A energia perdida pelo elétron nesse processo é convertida em um fóton de raios X, como . Esse processo é conhecido como bremsstrahlung. Do alemão bremss, que significa frenagem, e strahlung, que significa radiação, radiação de freamento.
Se a energia cinética do elétron após a desaceleração é K’, então, a energia do fóton gerado será:
Equação 1
ou, em termos de comprimento de onda,
Equação 2
Antes de chegar ao repouso, o elétron experimenta vários processos bremsstrahlung. As consequentes perdas de energia cinética resultam no espectro contínuo, observado anteriormente. O fóton de menor comprimento de onda, lmín, é emitido quando um elétron perde toda a sua energia cinética (K’ = 0) em um único processo de bremsstrahlung. Nesse caso, a equação torna-se:
Equação 3
ou, assumindo:
Equação 4
Assim, o limite mínimo dos comprimentos de onda corresponde a uma conversão completa da energia dos elétrons em fótons de raios X. A equação 4 mostra, explicitamente, que , que é a previsão clássica. Entretanto, é o fato de h ser diferente de zero que confere a uma manifestação da quantização de energia radiante.
RAIOS X CARACTERÍSTICOS
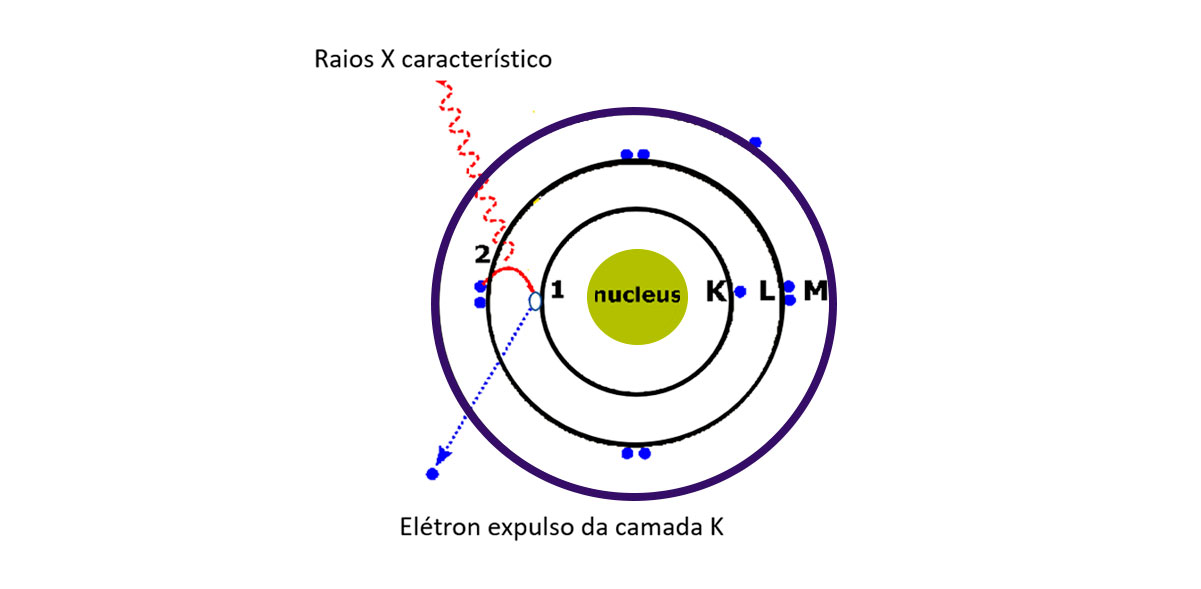
Por causa da grande tensão de aceleração, os elétrons incidentes podem:
Excitar elétrons nos átomos do alvo.
Ejetar elétrons fortemente ligados aos núcleos atômicos.
Atenção
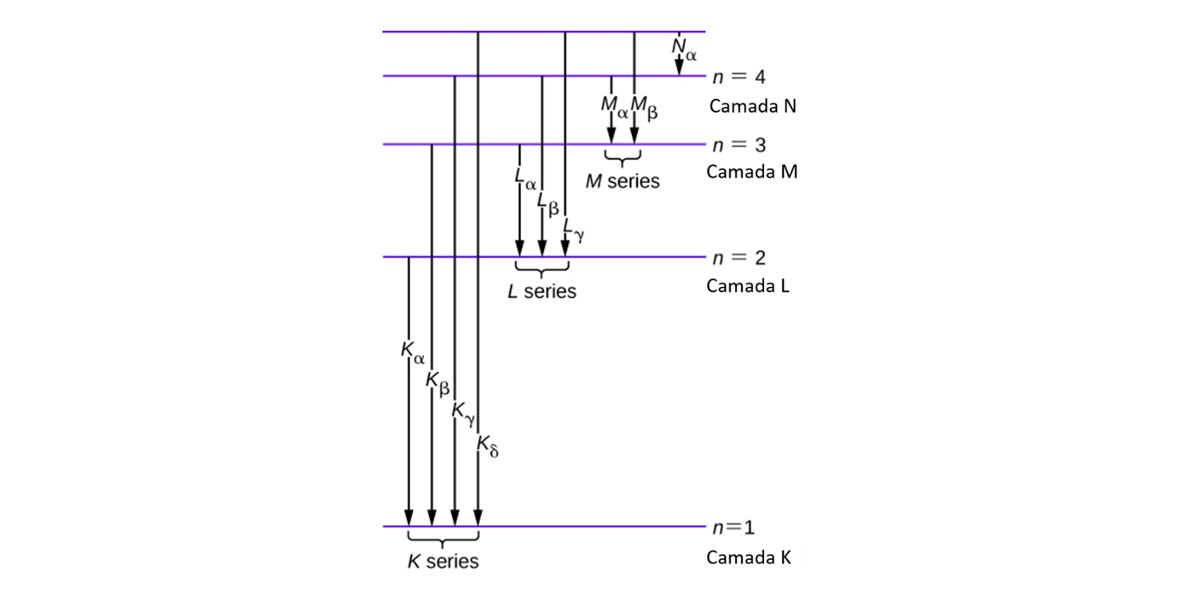
As transições para a camada L resultam na série L e aquelas para a camada M dão origem à série M, e assim por diante. Como os elétrons orbitais têm níveis de energia definidos, os fótons de raios X emitidos também têm energias bem definidas. O espectro de emissão possui linhas nítidas características do elemento alvo. Nem todas as transições são permitidas; apenas transições que cumprem as seguintes regras de seleção são permitidas: .
Difração de raios X e lei de Bragg
Em 8 de junho de 1912, Max von Laue anunciou sua descoberta da difração de raios X em cristais como rede de difração tridimensional.
O rápido desenvolvimento da Física na Europa do pré-guerra forneceu o pano de fundo necessário para essa descoberta que, por sua vez, resolveu o problema da natureza dos raios X e do tamanho dos átomos. Dois pesquisadores ingleses, Willian Henry Bragg e William Lawrence Bragg, pai e filho, demonstraram a relação que passou a ser conhecida como lei de Bragg, fundamental para o estudo de estruturas cristalinas com o uso da difração de raios X.
Os cristais são arranjos regulares de átomos e os raios X podem ser considerados ondas de radiação eletromagnética. Os átomos espalham ondas de raios X, principalmente através dos elétrons dos átomos. Assim como uma onda do oceano atingindo um farol produz ondas circulares secundárias que emanam do farol, um fóton de raios X atingindo um elétron produz ondas esféricas secundárias emanando do elétron.
Esse fenômeno é conhecido como espalhamento elástico e o elétron (ou farol) é conhecido como espalhador. Uma matriz regular de dispersores produz uma matriz regular de ondas esféricas. Embora essas ondas se cancelem na maioria das direções, por meio de interferência destrutiva, elas se somam de forma construtiva em algumas direções específicas, determinadas pela lei de Bragg.
Um plano de átomos em um cristal, também chamado de plano de Bragg, reflete os raios X, exatamente da mesma maneira que a luz é refletida de um espelho plano, como mostrado a seguir:
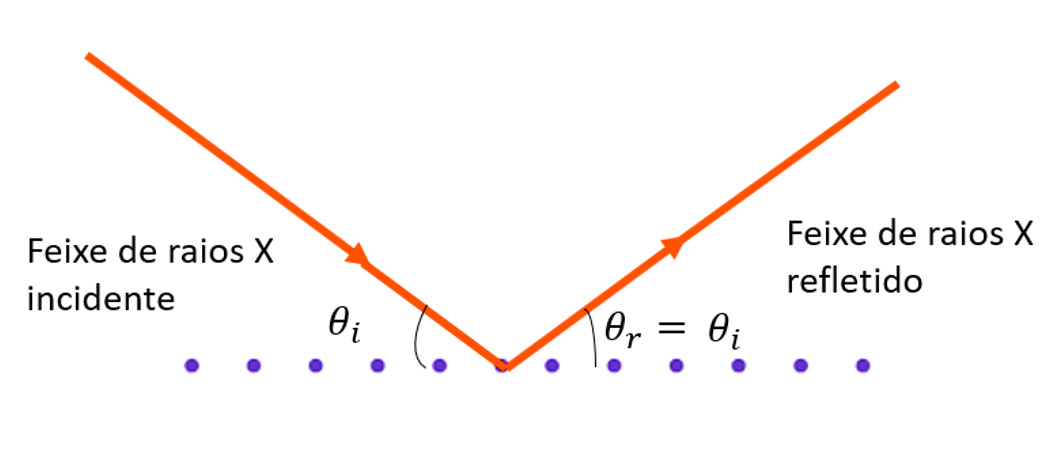
A reflexão de planos sucessivos pode interferir construtivamente se a diferença de caminho entre dois raios for igual a um número inteiro de comprimentos de onda.
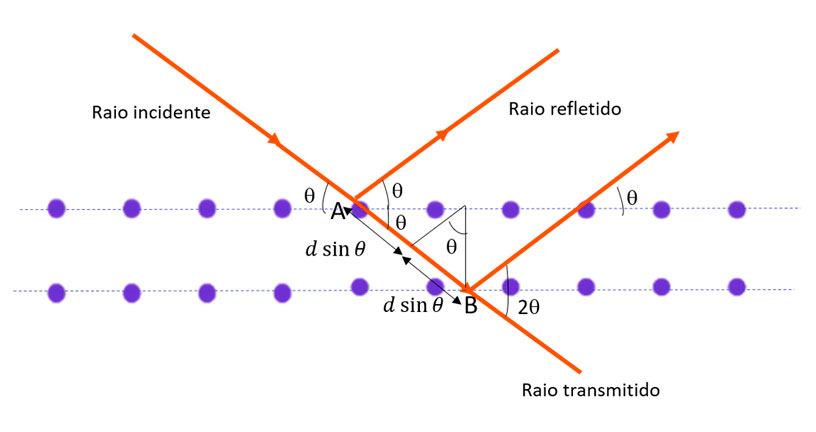
A distância , de modo que, pela lei de Bragg, temos:
Em que, na prática, é normal assumir difração de primeira ordem, de modo que n = 1.
Um determinado conjunto de planos atômicos dá origem a uma reflexão em um ângulo, vista como um ponto ou um anel em um padrão de difração, também chamado de difratograma.
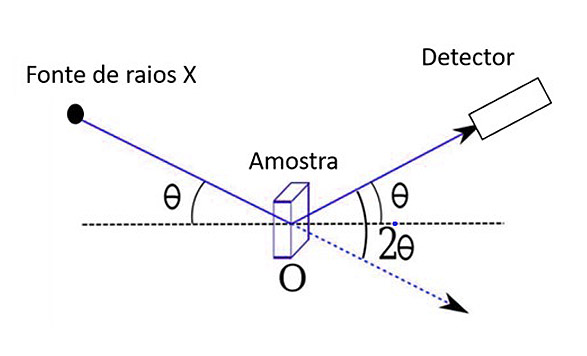
Técnicas de difração
As técnicas convencionais de difração usam amostras policristalinas compostas de muitas partículas finas, orientadas aleatoriamente e expostas à radiação de raios X monocromática. Cada partícula pulverizada é um cristal, e a presença de muitos cristais orientados aleatoriamente garante que a orientação de algumas partículas esteja correta, de modo que todos os planos cristalográficos possíveis possam ser usados para difração.
Um difratômetro é um dispositivo usado para determinar o ângulo no qual a difração ocorre em uma amostra pulverizada.
A plataforma e a amostra estão acopladas mecanicamente, tais que uma rotação da amostra por um ângulo θ é acompanhada de uma rotação de 2θ do contador. Isso assegura que os ângulos incidente e de reflexão sejam mantidos iguais. Colimadores são incorporados na trajetória do feixe para produzir um feixe focado e bem definido.
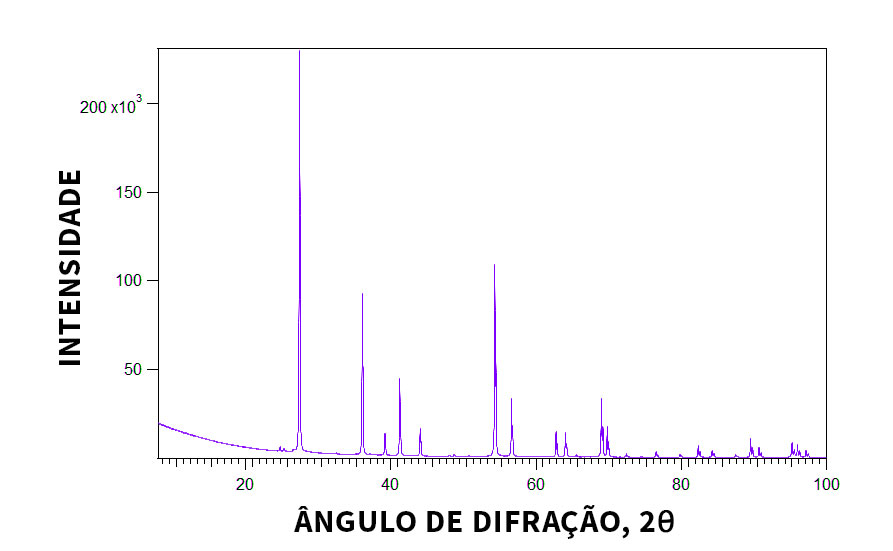
À medida que o contador se move a uma velocidade angular constante, um registrador traça, automaticamente, a intensidade do feixe difratado (monitorada pelo contador) em função de 2θ; 2θ é chamado de ângulo de difração e é medido experimentalmente.
A imagem anterior mostra um padrão de difração para uma amostra pulverizada de dióxido de titânio (TiO2). Os picos de alta intensidade ocorrem quando a condição de difração de Bragg é satisfeita por algum conjunto de planos cristalográficos.
Um dos principais empregos da difratometria de raios X é a determinação da estrutura cristalina. O tamanho e a geometria da célula unitária podem ser obtidos a partir das posições angulares dos picos de difração, enquanto o arranjo dos átomos no interior da célula unitária está associado às intensidades relativas desses picos.
Os raios X, bem como os feixes de elétrons e de nêutrons, também são usados em outros tipos de investigações dos materiais. Por exemplo, é possível determinar as orientações cristalográficas de monocristais usando fotografias de difração de raios X.
Outros usos para os raios X incluem identificações químicas qualitativas e quantitativas, além da determinação de tensões residuais e de tamanhos de cristais.
PRODUÇÃO E APLICAÇÕES DOS RAIOS X
Para concluir o módulo, a especialista Nilséia esclarecerá mais alguns pontos a respeito do tubo de raios X e suas diversas aplicações.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
Neste conteúdo, discutimos conceitos da natureza ondulatória e corpuscular da luz, bem como natureza, produção e aplicações dos raios X, enfatizando que a validade de todos os fatos científicos deve ser apoiada por um conjunto de técnicas, tecnologias e teorias.
A mecânica quântica aceita que uma onda eletromagnética ora se comporte como onda, produzindo interferência, difração e polarização, ora se comporte como partícula, como no efeito fotoelétrico ou na radiação térmica de um corpo negro.
Aceita, também, que as partículas podem, em certos fenômenos, ser difratadas e se comportar como onda, e que só é possível saber em que estado a radiação (luz, por exemplo) está depois que o fenômeno acontece.
Ou seja, identificar se a radiação se comporta como onda ou como partícula só é possível depois de observar o resultado de um experimento realizado. Por exemplo, no efeito fotoelétrico, a radiação irá se comportar como partícula, mas só percebemos isso após analisarmos os resultados do experimento; já em uma difração, através de uma fenda, só iremos notar um comportamento ondulatório observando o anteparo atingido pela luz depois de passar pela fenda. Ambas as teorias se complementam.
Podcast
Para encerrar o conteúdo, o podcast contribuirá com um debate importante: “Afinal, a luz é uma onda ou uma partícula?”
CONQUISTAS
Você atingiu os seguintes objetivos:
Analisou a natureza ondulatória da luz e o espectro eletromagnético em termos de frequência e comprimento de onda.
Identificou a natureza da luz na visão contemporânea e seu comportamento ondulatório e/ou corpuscular (dualidade onda-partícula).
Reconheceu a produção dos raios X e a importância de suas aplicações em diversas áreas.