Descrição

Introdução à análise de circuitos em corrente alternada (CA) em regime permanente senoidal, técnicas de análise de circuitos CA, circuitos CA trifásicos e potência CA.

PROPÓSITO

Compreender as relações entre tensão e corrente em regime de CA senoidal para fins de resolução de circuitos no domínio da frequência. Apresentar o sistema trifásico e a relação de potências em CA.

Preparação

Antes de iniciar o conteúdo deste tema, tenha em mãos papel, caneta e, se possível, uma calculadora científica para facilitar seus cálculos com números complexos.

OBJETIVOS

Módulo 1

Formular a relação entre tensão e corrente em regime permanente senoidal

Módulo 2

Aplicar técnicas de resolução de circuitos em CA no domínio da frequência

Módulo 3

Reconhecer sistemas trifásicos e relações de potência CA

NOÇÕES SOBRE CORRENTE ALTERNADA SENOIDAL

MÓDULO 1

Formular a relação entre tensão e corrente em regime permanente senoidal

RELAÇÃO ENTRE TENSÃO E CORRENTE EM REGIME PERMANENTE SENOIDAL

RELAÇÃO ENTRE TENSÃO E CORRENTE

As tensões senoidais disponibilizadas para uso em residências, indústrias e aplicações em geral são originadas em geradores de CA.

Entender a origem dos sinais alternados senoidais é o primeiro passo para aplicar as relações entre tensões e correntes alternadas para solução de circuitos com fontes variáveis.

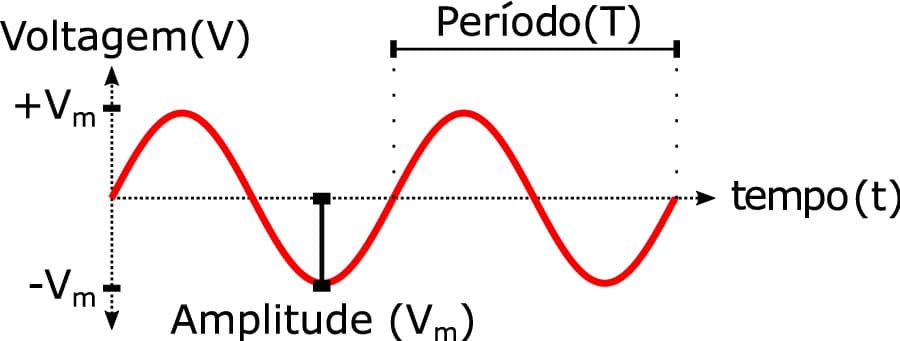
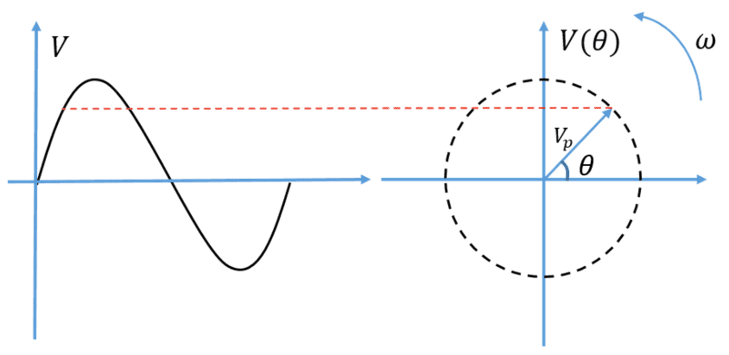
A figura a seguir ilustra a forma de onda de um sinal senoidal, que se repete em intervalos definidos. É possível dizer então que se trata de um sinal periódico.

Esse sinal periódico senoidal pode ser modelado por uma função cosseno (Equação 1). Por se tratar de um sinal que se repete, é possível obter sua frequência, que é o número de ciclos por segundo, medida em Hertz (Hz) ou radianos por segundo $(ω)$ .

$A_{m} \cos (ω t + \emptyset)$

(1)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

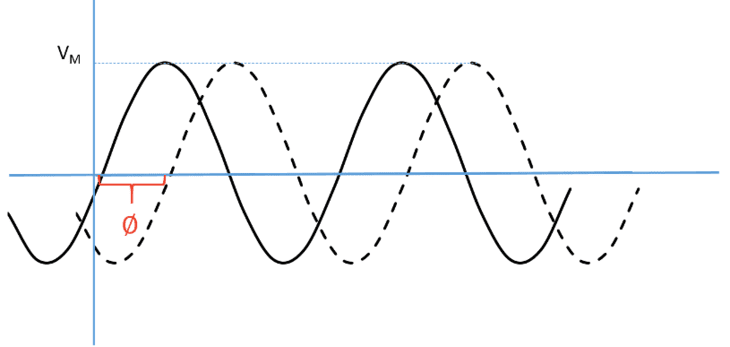
Na Equação 1 é possível ainda observar o ângulo ∅, denominado ângulo de fase do sinal senoidal. Ele determina o deslocamento da função no eixo de tempo (Figura 2). Essa forma de onda senoidal pode ser a representação de qualquer forma de onda alternada, como tensões, correntes ou potências.

O valor $V_{M}$ na figura acima refere-se ao valor máximo da amplitude do sinal, tanto no semiciclo positivo quanto no semiciclo negativo. Esse valor também é conhecido como valor de pico, de modo que a amplitude total, entre os valores máximos positivo e negativo, é denominada valor de pico a pico $V_{P P}$ , dado pela Equação 2:

$V_{P P} = 2 V_{M}$

(2)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A expressão matemática geral que representa um sinal senoidal é dada pela Equação 3.

$A_{m} sen (α)$

(3)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que $A_{m}$ é a amplitude máxima (de pico) do sinal e $α = ω t$ é o argumento do sinal, determinado pelo produto da frequência angular com o período do ciclo desse sinal.

Exemplo

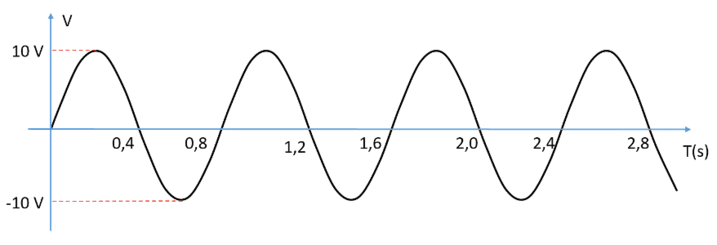
Considere a forma de onda de tensão senoidal da próxima figura. Essa tensão apresenta um valor de pico de 10 V, um período de oscilação de 0,8 s (tempo gasto para completar um ciclo de onda) e uma frequência de 1,25 Hz (quantidade de ciclos por segundo ou o inverso do período).

$f = \frac{1}{T}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que f é a frequência em Hertz e T, o período em segundos.

Exemplo

Sejam $v_{1} (t)$ e $v_{2} (t)$ duas tensões senoidais. Determine a frequência desses sinais em Hz e o ângulo de fase entre elas.

$v_{1} (t) = 10 s e n (377 t + 30 °) V$

$v_{2} (t) = 5 s e n (377 t - 20 °) V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A frequência em Hz é dada por:

$f = \frac{ω}{2 π} = \frac{377}{2 π} = 60 Hz$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Já o ângulo de fase entre os sinais é dado por:

$\emptyset = 30 ° - (- 20 °) = 50 °$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Valor médio de um sinal senoidal

O valor médio de um sinal senoidal é simplesmente a média desse sinal ao longo de um período.

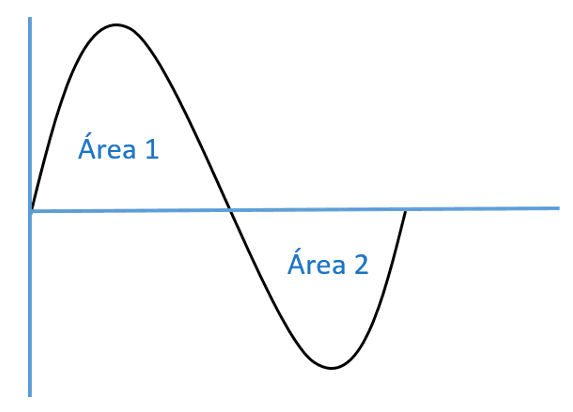
Tal valor pode ser entendido como a componente CC presente no sinal CA. Na figura a seguir o valor médio do sinal é a área sob a curva do gráfico.

Atenção

Para um sinal senoidal simétrico ao eixo x, a média será zero, pois os valores dos semiciclos positivo e negativo se anulam no cálculo da média.

Valor eficaz (rms) de um sinal senoidal

Saiba mais

O valor eficaz ou rms (do inglês root mean square, valor quadrado médio) refere-se à medida de um sinal CA que dissipa a mesma potência em uma resistência alimentada por um sinal CC.

O valor rms para sinais senoidais é dado pela Equação 4:

$A_{r m s} = \frac{A_{m}}{\sqrt{2}}$

(4)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que $A_{m}$ é a amplitude máxima ou de pico do sinal.

Comentário

As tensões indicadas pelas empresas de energia em instalações residenciais, por exemplo (127 V ou 220 V), já são valores rms.

Fasores

As expressões que representam um sinal CA senoidal, como o descrito na Equação 3, podem ser expressas de forma mais simplificada utilizando fasores.

Fasores são vetores que giram em círculo no sentido anti-horário a dada velocidade angular constante.

Para exemplificar como eles são representados, considere a Equação 5 que descreve uma tensão senoidal:

$V (t) = V_{m} c o s (ω t + θ)$

(5)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para descrever esse sinal de tensão completamente, basta conhecer seu valor máximo e seu ângulo de fase. Dessa forma, essa tensão pode ser representada por um número complexo na forma polar:

$V = V_{m} e^{j θ} = V_{m} ∠ θ$

(6)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A Equação 6 é definida como um fasor, representado em negrito para diferenciá-lo de outros números complexos.

Uma senoide pode ser representada por um conjunto de fasores de amplitude constante (Figura 5). Conforme o sinal senoidal ocorre ao longo do tempo, o fasor (vetor no ciclo trigonométrico) assume posições angulares (ou fases) diferentes.

Quando essa senoide completa um ciclo, o fasor completa um giro, de modo que pode ser denominado como um vetor girante.

Atenção

Grandezas defasadas – Quando duas ou mais senoides de mesma frequência não atingem seus respectivos valores máximos no mesmo instante do tempo, diz-se que elas estão defasadas.

Grandezas em fase – Quando duas ou mais senoides de mesma frequência (com a mesma amplitude ou não) atingem seus respectivos valores máximos no mesmo instante, diz-se que elas estão em fase.

Relação de tensão e corrente para fasores

Considerando que as tensões e correntes em um circuito de CA podem ser representadas na forma de fasores, é importante conhecer a relação entre essas grandezas para os elementos do circuito, ou seja:

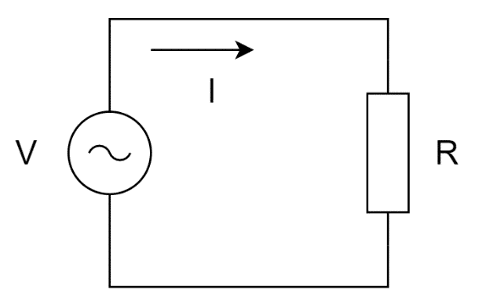
Resistores

Indutores

Capacitores

Essa relação tem como base a própria Lei de Ohm, com o fator de proporcionalidade sendo uma constante ou uma função da frequência $ω$ . No caso dos resistores, tem-se:

$V = Ri$

(7)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que:

$V (t) = V_{m} \cos (ωt + θ)$

(8)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$i (t) = I_{m} \cos (ωt + φ)$

(9)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Considerando as Equações 8 e 9 na forma polar e substituindo na Equação 7, a Lei de Ohm para os resistores será dada por:

$V_{m} e^{j θ} = R I_{m} e^{j φ}$

(10)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo $V_{m} e^{j θ}$ e $I_{m} e^{j φ}$ os fasores de tensão e corrente, respectivamente. Dessa forma, a representação fasorial para a relação entre tensão e corrente em resistores é:

$V = R I$

(11)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Atenção

Para os resistores, a relação fasorial no domínio da frequência é igual à relação do domínio do tempo, de modo que os ângulos de tensão $(θ)$ e corrente $(φ)$ são iguais e são ditos em fase.

Para o indutor, é preciso primeiro relembrar a sua relação no domínio do tempo:

$V (t)$ $= L \frac{d i (t)}{d t}$

(12)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A representação complexa da Equação 12 é dada pela Equação 13:

$V_{m} e^{j (ω t + θ)} = j ω L I_{m} e^{j (ω t + φ)}$

(13)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Assim, sua representação na forma de fasores é:

$V = j ω L I$

(14)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O fator de proporcionalidade para a Lei de Ohm aplicada ao indutor é $j ω L$ . A corrente será atrasada em 90° em relação à tensão.

Para o caso do capacitor, sua relação no domínio do tempo é dada por:

$i (t) = C \frac{d V (t)}{d t}$

(15)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir da mesma análise feita para o indutor, a Equação 15 pode ser fasorialmente representada por:

$I = j ω C V \Rightarrow V = \frac{I}{j ω C}$

(16)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A Equação 16 demonstra que a corrente e a tensão estão novamente fora de fase. Nesse caso, para o capacitor, a corrente está adiantada 90° em relação à tensão.

A Tabela 1 traz um resumo da relação entre tensão e corrente para os três componentes abordados: resistores, indutores e capacitores.

Elemento	Domínio do tempo	Domínio da frequência
$R$	$V = R i$	$V = R I$
$L$	$V = L \frac{d i}{d t}$	$V = j ω L I$
$C$	$i = C \frac{d v}{d t}$	$V = \frac{I}{j ω C}$

Tabela 1: Relação entre tensão e corrente nos elementos. Elaborado por Isabela Oliveira Guimarães.

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Teoria na prática

Considere que a equação senoidal a seguir representa tensão em um indutor. Utilizando os conceitos vistos anteriormente, converta essa tensão para sua representação na forma fasorial.

$V (t) = 5 c o s (20 t + 30 °) V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Considerando a representação geral de um sinal senoidal, conforme a Equação 5, tem-se:

$V (t) = V_{m} c o s (ω t + θ)$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para determinar sua representação fasorial, basta conhecer o valor máximo da tensão $V_{m}$ e seu ângulo de fase $(θ)$ :

$V = V_{m} e^{j θ} = V_{m} ∠ θ$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Assim, a representação fasorial do problema será dada por:

$V = 5 e^{j 30 °} = 5 ∠ 30 °$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

RESOLUÇÃO

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 2

Aplicar técnicas de resolução de circuitos em CA no domínio da frequência

TÉCNICAS DE RESOLUÇÃO DE CIRCUITOS CA NO DOMÍNIO DA FREQUÊNCIA

Reatância indutiva e capacitiva

Lembramos que um resistor, atravessado por uma corrente, apresenta uma oposição à passagem dessa corrente que chamamos de resistência.

O comportamento de uma resistência tanto na corrente contínua (CC) quanto na corrente alternada (CA) é o mesmo. O resistor, quando submetido a uma corrente, dissipa calor através do efeito Joule.

No entanto, quando tratamos de indutores e capacitores, há um comportamento diferente nos regimes de CC e CA. Um indutor em regime de CC funciona como um curto-circuito, mas, na CA, o indutor é carregado e descarregado na mesma frequência da senoide, o que gera um comportamento de oposição à passagem da corrente alternada. Esse efeito, semelhante ao da resistência, é a reatância indutiva, e é representado por $X_{L}$ .

Um capacitor em regime de CC funciona como um circuito aberto, mas na CA o capacitor é carregado e descarregado na mesma frequência da senoide, o que gera um comportamento de oposição à passagem da corrente alternada. Esse efeito, semelhante ao da resistência, é a reatância capacitiva, e é representado por $X_{C}$ .

Impedância do circuito

Em CA, a relação entre tensão e corrente referente às resistências e reatâncias do circuito, deve ser feita utilizando fasores, conforme detalhado no Módulo 1.

Tal relação normalmente resulta na expressão dos componentes do circuito como números complexos, o que será tratado como a impedância de cada elemento.

Considere as relações entre tensão e corrente para os três componentes estudados: resistor, indutor e capacitor no domínio da frequência.

$V = R I V = j ω L I V = \frac{I}{j ω C}$

(17)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Essas relações são a representação da Lei de Ohm na forma fasorial, de modo que é possível reescrevê-las como:

$\frac{V}{I} = R \frac{V}{I} = j ω L \frac{V}{I} = \frac{1}{j ω C}$

(18)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Nessa representação, a relação $\frac{V}{I}$ é chamada de impedância do dispositivo, representada por $Z$ , medida em ohms $(Ω)$ . Apesar de ser dada pela relação entre dois fasores, a impedância não pode ser considerada um fasor, visto que não varia como uma senoide. A impedância dos três componentes de circuito ( $R$ , $L$ e $C$ ) é dada por:

$R \Rightarrow Z = R$

$L \Rightarrow Z = j ω L$

$C \Rightarrow Z = \frac{1}{j ω C}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Dessa forma, a impedância de um componente pode ser definida como sua capacidade de se opor a uma corrente senoidal, que possui módulo e frequência.

Atenção

Para o resistor (também chamado de elemento ativo), é possível observar que a impedância é seu próprio valor de resistência à oposição de passagem de corrente. Para os indutores e capacitores (também chamados de elementos passivos), sua impedância será o que definimos com reatância $X$ . A impedância também pode representar as características de partes ou de todo um circuito formado pelos elementos $R$ , $L$ e $C$ .

Assim, para um circuito elétrico, a impedância pode ser apresentada como a combinação entre as partes ativa e reativa do circuito por um número complexo em sua forma retangular:

$Z = R + j X$

(19)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Na Equação 19, $R$ corresponde à parcela ativa (ou resistiva) do circuito, enquanto $X$ corresponde à parcela reativa, também denominada reatância do circuito.

Você sabia

A impedância é considerada indutiva quando $X$ é positiva ou capacitiva quando $X$ é negativa. Do mesmo modo que a impedância, a reatância também é medida em ohms.

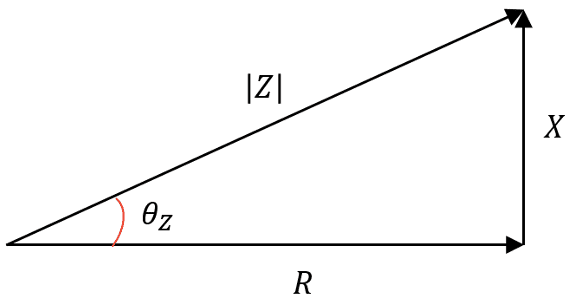
A partir das relações trigonométricas de números complexos, é possível calcular o módulo e o ângulo da impedância de um circuito a partir de suas componentes resistivas e reativas:

$|Z| = \sqrt{R^{2} + X^{2}}$

(20)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$θ_{Z} = t a n^{- 1} \frac{X}{R}$

(21)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Graficamente, essas relações são representadas da seguinte forma:

Exemplo

Em um circuito elétrico alimentado com corrente senoidal, os componentes são desconhecidos, e foram medidas as seguintes grandezas fasoriais: $V = 10 ∠ 46,9 °$ e $I = 2 ∠ 10 °$ . A impedância desse circuito será dada por:

$Z = \frac{10 ∠ 46,9 °}{2 ∠ 10 °} = 5 ∠ 36,9 ° Ω$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir da Equação 20 é possível determinar a impedância em sua forma retangular, de modo a extrair suas componentes resistivas e reativas:

$Z = 5 (\cos 46,9 ° + jcos 10 °)$

$Z = 4 + j 3 Ω$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Ou seja, o circuito descrito possui uma resistência de $4 Ω$ e uma reatância indutiva de $3 Ω$ .

Admitância do circuito

Em muitas situações de análise, é indicado solucionar circuitos utilizando a grandeza inversa da impedância $(Z)$ . A admitância $(Y)$ é a grandeza inversa à impedância (análoga à condutância em circuitos CC), cuja unidade de medida é siemens (ou mhos):

$Y = \frac{1}{Z}$

(22)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Do mesmo modo que a impedância, a admitância é um número complexo; logo, pode ser descrita em seu formato retangular:

$Y = G + j B$

(23)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que $G = Re, Y$ é chamada condutância e $B = Im Y$ é a susceptância

$G + j B = \frac{1}{R + j X}$

(24)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Atenção

O fato de inverter separadamente a resistência ou a reatância de um circuito não fornece a condutância e susceptância correspondentes. Por se tratar de grandezas complexas, o cálculo leva em conta as relações trigonométricas:

$G = \frac{R}{R^{2} + X^{2}} B = - \frac{X}{R^{2} + X^{2}}$

(25)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Leis de Kirchhoff para análise de circuitos CA

Da mesma forma que na análise de circuitos CC, as Leis de Kirchhoff das Tensões (LKT) e das Correntes (LKC) são igualmente válidas para análise de circuitos CA no domínio da frequência, através dos fasores.

Para a LKT, o somatório das tensões em uma malha de circuito é zero, de modo que, na forma fasorial, tem-se:

$V_{1} + V_{2} + \dots + V_{n} = 0$

(26)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que:

$V_{n} = V_{n} ∠ θ_{n}, n = 1,2, 3, \dots . . n$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para a LKC, é válida relação semelhante. O somatório das correntes em um nó de circuito é zero, de modo que, na forma fasorial, tem-se:

$I_{1} + I_{2} + \dots + I_{n} = 0$

(27)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo:

$I_{n} = I_{n} ∠ θ_{n}, n = 1,2, 3, \dots . . n$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

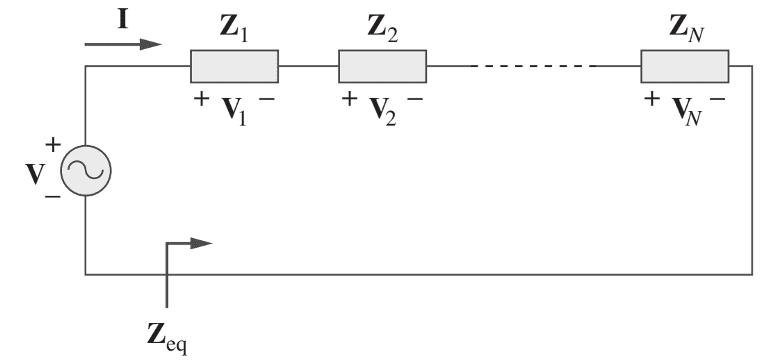
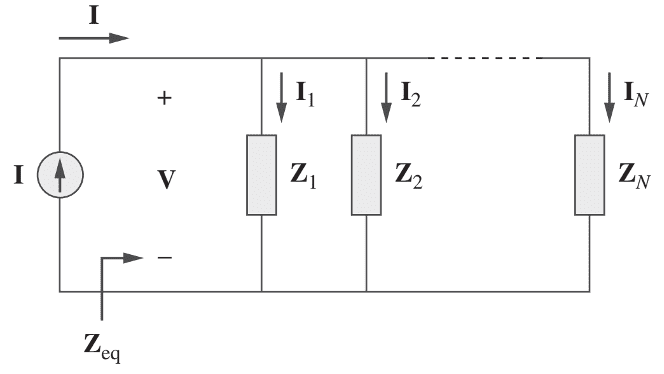
Em um circuito que contém N impedâncias associadas em série e alimentadas por uma fonte senoidal (Figura 8), fluirá uma única corrente fasorial através de todos os elementos, conforme as Leis de Kirchhoff. Dessa forma, a tensão em cada um será dada por:

$V_{1} = Z_{1} I, V_{2} = Z_{2} I, V_{3} = Z_{3} I, \dots, V_{n} = Z_{n} I$

(28)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir da LKT:

$V = V_{1} + V_{2} + \dots + V_{n}$

$V = (Z_{1} + Z_{2} + \dots + Z_{n}) I = 0$

$V = Z_{eq} I$

(29)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo $Z_{eq}$ a impedância equivalente, dada pelo somatório das impedâncias ligadas em série no circuito:

$Z_{e q} = Z_{1} + Z_{2} + \dots + Z_{n}$

(30)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

É fácil observar que o cálculo da impedância equivalente é semelhante ao cálculo de resistência equivalente em circuitos CC. De modo semelhante, o inverso complexo da impedância é a admitância $Y = \frac{1}{Z}$ , muito conveniente em circuitos com componentes ligados em paralelo, conforme Figura 9:

$I = I_{1} + I_{2} + \dots + I_{n}$

$I = V (\frac{1}{Z_{1}} + \frac{1}{Z_{2}} + \dots + \frac{1}{Z_{n}})$

(31)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Neste caso, a impedância equivalente é dada por

$\frac{1}{Z_{e q}} = \frac{I}{V} = \frac{1}{Z_{1}} + \frac{1}{Z_{2}} + \dots + \frac{1}{Z_{n}}$

(32)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

E a admitância equivalente é dada por

$Y_{e q} = Y_{1} + Y_{2} + \dots + Y_{n}$

(33)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Exemplo

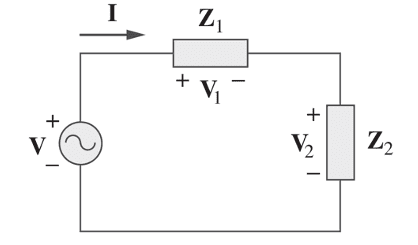
Para o circuito da figura abaixo, com duas impedâncias ligadas em série e alimentadas por uma fonte senoidal, as tensões $V_{1}$ e $V_{2}$ são dadas por:

$V_{1} = Z_{1} I$

$V_{2} = Z_{2} I$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$V_{1} = \frac{Z_{1}}{Z_{1} + Z_{2}} V V_{2} = \frac{Z_{2}}{Z_{1} + Z_{2}} V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Essa é a mesma relação de divisor de tensão já conhecida para circuitos CC. A relação de divisor de corrente também é válida em circuitos com impedâncias ligadas em paralelo.

Análise nodal

As relações entre tensão e corrente são igualmente válidas em circuitos alimentados com fontes alternadas, de modo que as Leis de Kirchhoff das tensões e correntes podem ser aplicadas na análise de circuitos. O método de análise nodal para circuitos com fasores é demonstrado no exemplo a seguir, utilizando a LKC.

Exemplo

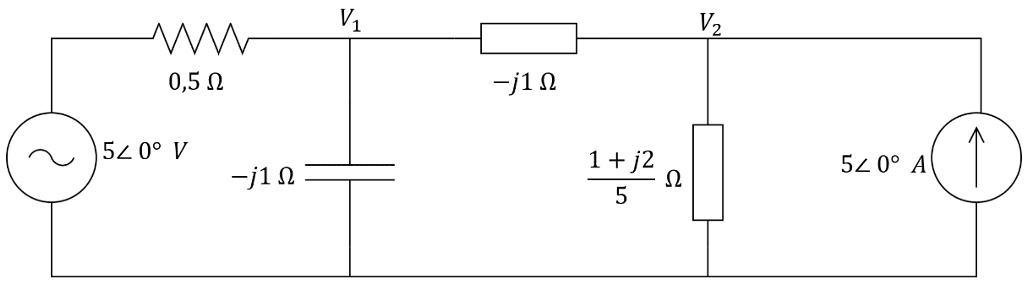
Determine $V_{1}$ e $V_{2}$ no circuito a seguir utilizando a análise nodal.

É necessário aplicar a LKC aos nós 1 e 2. Suas equações serão:

Para o nó 1:

$\frac{V_{1} - 5 ∠ 0 °}{0,5} + \frac{V_{1}}{- j 1} + \frac{V_{1} - V_{2}}{- j 1} = 0$

$(2 + j 2) V_{1} - j V_{2} = 10$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para o nó 2:

$\frac{V_{2} - V_{1}}{- j 1} + \frac{V_{2}}{0,2 + j 0,4} = 5 ∠ 0 °$

$- j V_{1} + (1 - j) V_{2} = 5$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

As equações dos nós 1 e 2 podem ser representadas matricialmente:

$[\begin{matrix} 2 + j 2 & - j \\ - j & 1 - j \end{matrix}] [\begin{matrix} V_{1} \\ V_{2} \end{matrix}] = [\begin{matrix} 10 \\ 5 \end{matrix}]$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Resolvendo o sistema linear, os valores de $V_{1}$ e $V_{2}$ são:

$V_{1} = 2 - j = 2,23 ∠ - 26,6 ° V$

$V_{2} = 2 + j 4 = 4,47 ∠ 63,4 ° V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Análise de malhas

Com base na LKT é possível formular o método de análise de malhas para solução de circuitos com fasores. Veja sua aplicação ilustrada a seguir:

Exemplo

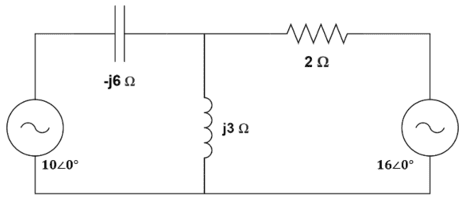
Utilizando análise de malhas, determine as correntes $I_{1}$ e $I_{2}$ no circuito abaixo:

Aplicando a LKT à malha 1, tem-se:

$- 10 ∠ 0 ° - j 6 I_{1} + j 3 (I_{1} - I_{2}) = 0$

$- j 3 I_{1} - j 3 I_{2} = 10 ∠ 0 °$

$j 3 (I_{2} - I_{1}) + 2 I_{2} + 16 ∠ 0 ° = 0$

$- j 3 I_{1} + (2 + j 3) I_{2} = - 16 ∠ 0 °$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

As equações das malhas 1 e 2 podem ser representadas matricialmente como:

$[\begin{matrix} - j 3 & - j 3 \\ - j 3 & 2 + j 3 \end{matrix}] [\begin{matrix} I_{1} \\ I_{2} \end{matrix}] = [\begin{matrix} 10 \\ - 16 \end{matrix}]$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Resolvendo o sistema linear, as correntes $I_{1}$ e $I_{2}$ são:

$I_{1} = 1,7 ∠ - 23,5 ° A$

$I_{2} = 7,1 ∠ 108 ° A$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Teoremas de rede

Exceto pela característica variante no tempo das tensões e correntes senoidais, os teoremas utilizados para análise CC são igualmente válidos a circuitos fasoriais lineares.

Clique nas informações a seguir. Clique nas informações a seguir.

Superposição

Transformação de fontes

Thévenin

Norton

Superposição

O teorema da superposição, para circuitos elétricos, afirma que a corrente elétrica total em qualquer ramo de um circuito bilateral linear é igual à soma algébrica das correntes produzidas por cada fonte atuando separadamente no circuito.

Transformação de fontes

O teorema da transformação permite converter fontes de tensão com resistência interna em fontes de corrente.

Thévenin

O teorema de Thévenin estabelece que qualquer circuito linear visto de um ponto, pode ser representado por uma fonte de tensão em série com uma impedância.

Norton

O teorema de Norton afirma que qualquer fontes de tensão, fonte de corrente, e resistor, com dois terminais, é eletricamente equivalente a uma fonte de corrente ideal, $I$ , em paralelo com um único resistor, $R$ .

Atenção

Em circuitos com fontes múltiplas operando com frequências diferentes, a resposta final deve ser dada pela soma das contribuições dessas fontes no domínio do tempo, visto que não se deve somar fasores com frequências distintas.

Teoria na prática

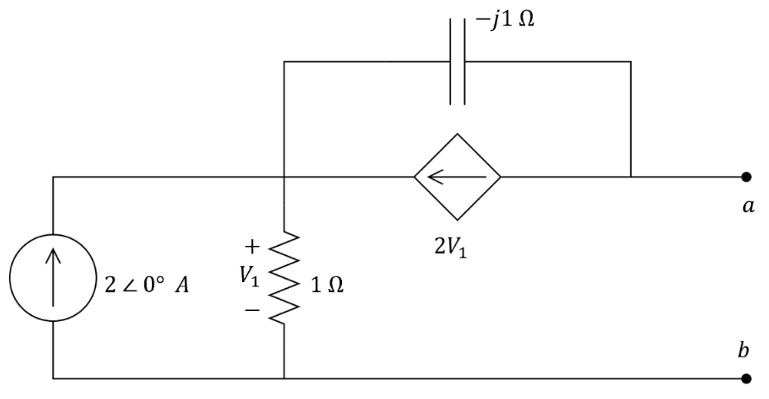
Determine o circuito equivalente de Thévenin para os pontos a e b:

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Para encontrar a impedância equivalente de Thévenin, é necessário desativar as fontes do circuito. Neste caso, as fontes de corrente são um circuito aberto:

$Z_{t h} = 1 + (- j 1) = 1 - j 1 Ω$

$V_{1} = 2 . 1 = 2 V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Aplicando a LKT na malha que contém os pontos a e b, encontra-se a tensão equivalente de Thévenin:

$V_{t h} = V_{1} - (- j 1) 2 V_{1} = 2 (1 + j 2) = 2 + j 4 V$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

RESOLUÇÃO

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 3

Reconhecer sistemas trifásicos e relações de potência CA

POTÊNCIA CA E SISTEMAS TRIFÁSICOS

Potências

Em virtude das limitações dos componentes em eletricidade, a potência é uma das mais importantes grandezas a se conhecer para o funcionamento correto de um circuito.

A potência elétrica está diretamente relacionada com a capacidade de transferência de energia entre partes do circuito, de modo que não deve ser permitida a operação acima da chamada potência nominal, que é o máximo valor admissível para aquele componente sem que seja causado algum dano.

A partir das relações entre tensão e corrente em regime senoidal, é possível definir os principais conceitos relacionados à potência em corrente alternada (CA), como potência:

Instantânea

Média

Eficaz

Complexa

A potência instantânea $P (t)$ de um circuito é o produto da tensão instantânea $V (t)$ com a corrente instantânea $I (t)$ , sendo medida em watts (W)

$P (t) = V (t) i (t)$

(34)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A potência instantânea varia com o tempo, de modo que é muito difícil medi-la, em virtude da frequência do sinal alternado, normalmente 60 Hz.

Uma forma comum de se medir potência em circuitos com CA é através da potência média $P$ , que se refere à média da potência instantânea ao longo de um período do sinal alternado. Matematicamente, a potência média é dada por:

$P = \frac{1}{T} \int_{0}^{T} P (t) d t = \frac{1}{2} V_{m} I_{m} \cos (θ_{V} - θ_{i})$

(35)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que $V_{m}$ e $I_{m}$ são os valores máximos da tensão e corrente, $θ_{v}$ e $θ_{i}$ são os ângulos dos fasores de tensão e corrente. Já em circuitos puramente resistivos, $θ_{v} = θ_{i}$ , de modo que a Equação 35 corresponde a uma potência nula. Dessa forma, é fácil perceber que em circuitos resistivos a potência é máxima.

Atenção

Em circuitos reativos (indutivos ou capacitivos), $θ_{v} - θ_{i} = \pm 90 °$ , ou seja, a potência média é zero para circuitos puramente reativos.

A potência eficaz é a quantidade de potência entregue por uma fonte alternada que depende de sua forma de onda.

Dessa maneira, é preciso utilizar um método capaz de comparar essa potência fornecida por diferentes fontes, o que é possível medindo os valores eficazes dessa fonte, ou rms (do inglês root mean square, valor quadrado médio).

O valor eficaz de uma CA (periódica) é a medida de corrente contínua (CC) que libera a mesma potência média da CA em uma carga resistiva. Essa equivalência é representada na Equação 36.

$P = {RI}_{ef}^{2} = \frac{1}{T} \int_{0}^{T} {Ri}^{2} dt$

(36)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Portanto, tensão e corrente eficazes (ou rms) podem ser descritas como:

$I_{ef} = I_{rms} = \sqrt{\frac{1}{T} \int_{0}^{T} i^{2} dt} V_{ef} = V_{rms} = \sqrt{\frac{1}{T} \int_{0}^{T} v^{2} dt}$

(37)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para o caso específico de sinais senoidais, que representam a forma de onda de tensão e corrente da rede elétrica, o valor eficaz da corrente será:

$i (t) = I_{m} \cos (ωt)$

$I_{ef} = \sqrt{\frac{1}{T} \int_{0}^{T} I_{m}^{2} \cos^{2} (ωt) dt} = \frac{I_{m}}{\sqrt{2}}$

(38)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A potência média de um sinal senoidal pode ser reescrita a partir dos valores eficazes da tensão e corrente:

$P = V_{ef} I_{ef} \cos (θ_{v} - θ_{i})$

(39)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Os valores de tensão que são fornecidos pelas empresas de energia para alimentação dos consumidores já são representados por seus valores eficazes.

A potência aparente (S) é o produto de tensão e corrente eficazes de uma fonte.
O termo $\cos (θ_{v} - θ_{i})$ é o fator de potência $(f p)$ .
A S é medida em volt-ampère (VA) para diferenciá-la da potência média, que é medida em Watts (W).

A razão entre a potência média e a potência aparente em uma carga é o próprio $f p$ , que é adimensional:

$f p = \frac{P}{S} = \cos (θ_{v} - θ_{i})$

(40)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O $f p$ também pode ser definido como o ângulo da carga (ou ângulo da impedância), que é o ângulo formado pelos fasores de tensão e corrente, conforme descrito a seguir:

$Z = \frac{V}{I} = \frac{V_{e f}}{I_{e f}} = \frac{V_{e f}}{I_{e f}} ∠ θ_{v} - θ_{i}$

(41)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O $f p$ é uma grandeza que relaciona a potência média com a potência aparente entregue a uma carga, de modo que seu valor varia entre zero e um.

Veja como se dá o $f p$ nos tipos de cargas abaixo:

Em uma carga puramente resistiva, a diferença entre os ângulos da tensão e corrente é zero, o que faz com que o $f_{p}$ seja um, ou unitário.

Em cargas puramente reativas (indutivas ou capacitivas), o $f_{p}$ é zero, pois $θ_{v} - θ_{i} = \pm 90 °$ , o que significa que a potência média é nula.

Em cargas reativas o $f_{p}$ pode estar adiantado (quando o ângulo da corrente é adiantado em relação ao ângulo da tensão) ou atrasado (quando o ângulo da tensão é adiantado em relação ao ângulo da corrente).

Exemplo

Uma carga drena de uma fonte senoidal uma corrente $i (t) = 5 \cos (ω t + 25 °)$ A. Essa fonte tem uma tensão $v (t) = 100 \cos (ω t - 15 °) V$ . Para essa carga, a potência aparente e seu fator de potência são dados por:

$S = V_{e f} I_{e f} = \frac{100}{\sqrt{2}} \frac{5}{\sqrt{2}} = 250 V A$

$F P = \cos (θ_{v} - θ_{i}) = \cos (- 15 ° - 25 °) = 0,76$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Esse $f p$ está adiantado, pois o ângulo da corrente é adiantado em relação ao ângulo da tensão.

Potência complexa é o termo dado à contribuição de toda a potência aparente (parte real e imaginária) nas cargas de um circuito.

Para uma carga alimentada por uma tensão e corrente senoidais, a potência complexa é dada pelo produto dos fasores de tensão e conjugado da corrente:

$S = \frac{1}{2} V I^{*}$

(42)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em termos de valores eficazes:

$S = V_{e f} I_{e f}^{*}$

(43)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Saiba mais

O módulo da potência complexa é a potência aparente, de maneira que sua unidade também é o volt-ampère (VA). Da mesma forma, seu ângulo corresponde ao fator de potência da carga.

Essa potência pode ser escrita em função de sua parte real e imaginária. A parte real $(P)$ corresponde à potência ativa (ou potência real) absorvida pela carga e medida em watts (W), enquanto a parte imaginária $(Q)$ corresponde à potência reativa trocada entre fonte e carga, medida em volt-ampère reativo (Var).

$S = P + j Q$

(44)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que:

$Q = 0$ para cargas resistivas ( $f_{p}$ unitário);

$Q < 0$ para cargas capacitivas ( $f_{p}$ adiantado);

$Q > 0$ para cargas indutivas ( $f_{p}$ atrasado).

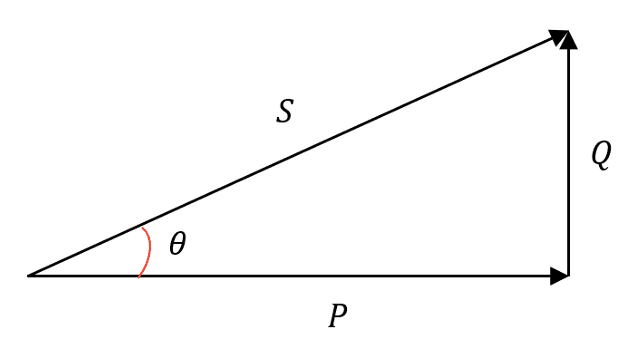
Normalmente, a relação de potências complexa, ativa e reativa é representada a partir de um triângulo de potências (Figura 21).

Do triângulo de potências é possível extrair informações a respeito da potência aparente, potência ativa, potência reativa e do fator de potência, utilizando relações trigonométricas do triângulo retângulo.

Exemplo

Uma carga absorve uma potência de 1.000 VA, com fator de potência 0,6 adiantado. A partir da definição de triângulo de potências, as potências ativa e reativa são dadas por:

$f_{p} = \frac{P}{S} \Rightarrow P = f_{p} \times S$

$P = 0,6 \times 1.000 = 600 W$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir do teorema de Pitágoras aplicado ao triângulo de potências, é possível determinar a potência reativa, $Q$ :

$Q = \sqrt{S^{2} - P^{2}} = \sqrt{{1.000}^{2} - 600^{2}} = 800 V A r$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

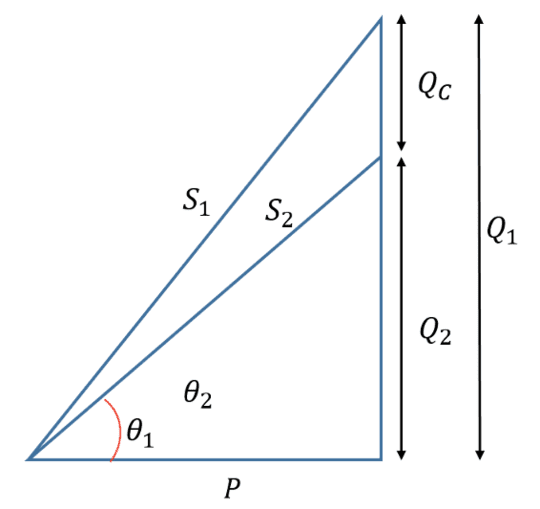
Correção do fator de potência

O fator de potência é um indicativo do percentual de energia consumida pela carga que é efetivamente utilizada para produzir trabalho, ou seja, relaciona a potência ativa real da carga com a potência aparente.

Muitas cargas do sistema têm características indutivas ou capacitivas, como é o caso de eletrodomésticos com motores, lâmpadas eletrônicas e até mesmo cargas industriais, como os fornos de indução. Essas cargas fazem com que o fator de potência da instalação caia para valores fora dos recomendados pelas concessionárias de energia. Para mitigar esse problema, é feita a correção de fator de potência.

Essa correção consiste em instalar equipamentos capazes de compensar o excesso ou a falta de reativos na carga para reduzir o ângulo entre os fasores de tensão e corrente. Por exemplo, em uma carga com características indutivas de baixo fator de potência, é possível fazer uma correção instalando capacitores em paralelo com a carga, de modo a reduzir a potência reativa consumida.

É importante observar que, após a correção, a potência ativa drenada pela carga permanece inalterada, enquanto o módulo da potência aparente é reduzido. Dessa forma, a corrente drenada da rede será menor, o que permite dizer que a correção de fator de potência permite reduzir até mesmo o carregamento dos circuitos de alimentação.

Sistemas trifásicos

A geração de energia em sistemas elétricos de potência é feita em sistemas com mais de uma fase (ou polifásicos), mais comumente a partir do sistema trifásico.

Você sabia

A geração de energia em CA trifásica traz muitos benefícios ao sistema, tanto econômicos quanto operacionais. A geração em sistemas trifásicos permite a conexão de cargas de maior potência através das linhas de transmissão. A energia é transportada em tensões elevadas para reduzir as perdas ôhmicas nas linhas, o que corresponde a menores custos de operação para as empresas do setor elétrico.

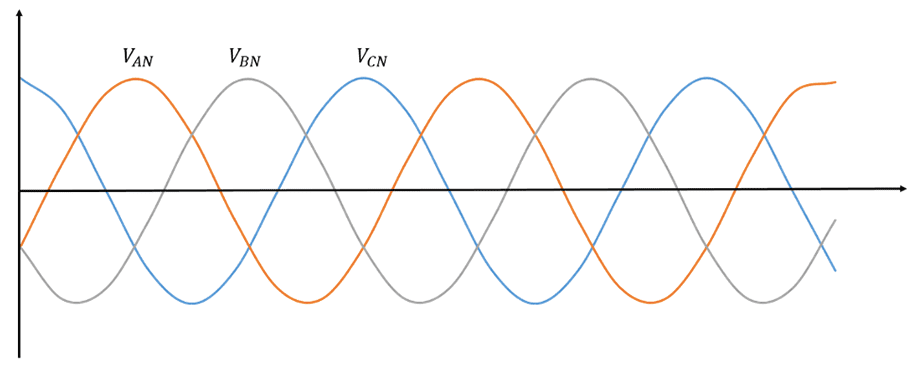
Uma fonte trifásica é obtida a partir de geradores CA, cujos enrolamentos responsáveis pela indução da corrente nos terminais de saída são defasados em 120° em torno do eixo da máquina. Essa defasagem produz tensões iguais e defasadas de 120° elétricos umas das outras. Veja as senoides geradas em um sistema trifásico:

As tensões $V_{A N}$ , $V_{B N}$ e $V_{C N}$ referem-se às tensões nas fases $A$ , $B$ e $C$ disponíveis nos terminais de um gerador CA trifásico.

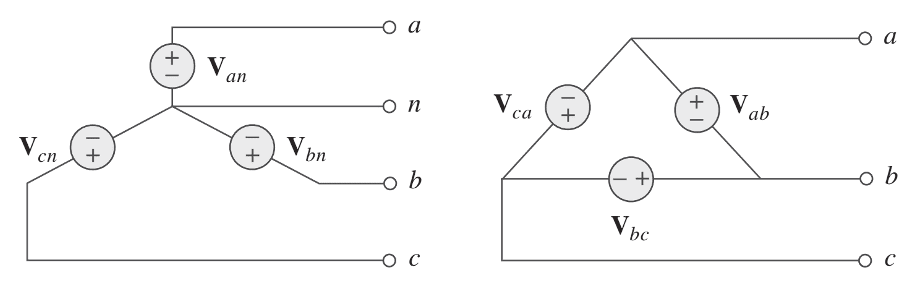
Um sistema trifásico é equivalente a três sistemas monofásicos e podem ser representados por uma ligação em estrema ou em triângulo, conforme a figura:

Em circuitos trifásicos equilibrados, cuja corrente e tensão são iguais nas três fases, são válidas as seguintes expressões:

Fonte ligada em triângulo $(∆)$

$V_{A N} + V_{B N} + V_{C N} = 0 \Rightarrow |V_{A N}| = |V_{B N}| = |V_{C N}|$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Fonte ligada em estrela $(Y)$

$I_{A} + I_{B} + I_{C} = 0 \Rightarrow |I_{A}| = |I_{B}| = |I_{C}|$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Ou seja, a soma fasorial das tensões na ligação em triângulo equilibrado é zero e das correntes na ligação em estrela é zero.

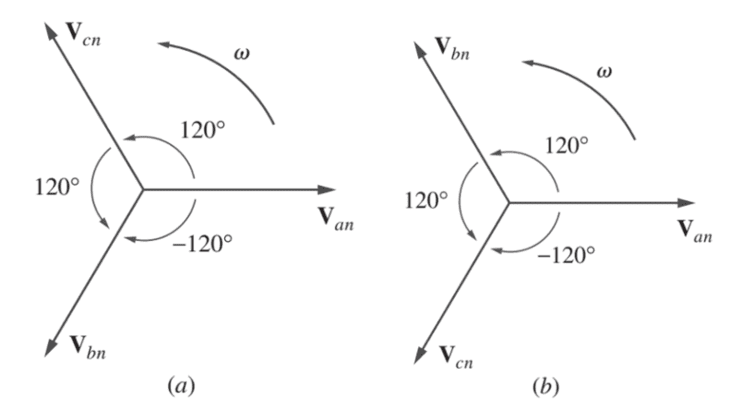
Veja os diagramas fasoriais que representam essa relação:

Tomando a tensão como exemplo, os fasores podem ser expressos de duas formas:

Se os fasores giram no sentido anti-horário, diz-se que a fonte está em sequência positiva, ou seja, $V_{A N}$ é adiantada em relação a $V_{B N}$ , que por sua vez é adiantada em relação a $V_{C N}$ .
Se os fasores giram no sentido horário, é dito que a fonte está em sequência negativa.

Os fasores de sequência positiva e negativa para as tensões trifásicas são:

Sequência positiva	Sequência negativa
$V_{A N} = V_{p} ∠ 0 °$	$V_{A N} = V_{p} ∠ 0 °$
$V_{B N} = V_{p} ∠ - 120 °$	$V_{B N} = V_{p} ∠ + 120 °$
$V_{C N} = V_{p} ∠ + 120 °$	$V_{C N} = V_{p} ∠ - 120 °$

Tabela 2: Relações de tensão em sistemas trifásicos equilibrados.

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Circuitos trifásicos equilibrados

Normalmente, circuitos trifásicos equilibrados (fonte e carga equilibrados) são facilmente solucionados a partir de seu circuito monofásico equivalente. Apenas os circuitos ligados em Y podem ser resolvidos a partir de seu circuito equivalente por fase, de modo que, caso fonte ou carga esteja ligada em triângulo, deve ser convertida para seu equivalente em ligação estrela, conforme a Equação 45, que representa a impedância da carga trifásica:

$Z_{Y} = \frac{Z_{∆}}{3}$

(45)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir da relação entre os fasores (Figura 25), as correntes e tensões nos circuitos equilibrados para as ligações em triângulo e estrela são dadas por:

Circuito em $∆$

$I_{ϕϕ} = \sqrt{3} I_{ϕ}$

$V_{ϕϕ} = V_{ϕ}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Circuito em $Y$

$I_{ϕϕ} = I_{ϕ}$

$V_{ϕϕ} = \sqrt{3} V_{ϕ}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Em que $I_{ϕϕ}$ e $V_{ϕϕ}$ são corrente e tensão de linha (entre fases) e $I_{ϕ}$ $V_{ϕ}$ são corrente e tensão de fase (em relação ao neutro).

Potência trifásica

Em cargas trifásicas equilibradas, ligadas em triângulo ou estrela, as correntes que circulam pelas linhas que as alimentam são iguais, de modo que a potência trifásica é dada pelo somatório da potência nas três fases. Para uma carga ligada em estrela:

$P_{ϕ} = V_{ϕ} . I_{ϕ} . \cos (φ)$

$P_{3 ϕ} = 3 . V_{ϕ} . I_{ϕ} . \cos (φ)$

(46)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Da Tabela 2:

$V_{ϕϕ} = \sqrt{3} V_{ϕ}$

$I_{ϕϕ} = I_{ϕ}$

A potência complexa na carga pode ser reescrita em função dos valores de linha da tensão e corrente:

$S_{3 ϕ} = \sqrt{3} . V_{ϕϕ} . I_{ϕϕ}$

(47)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$P_{3 ϕ} = \sqrt{3} . V_{ϕϕ} . I_{ϕϕ} . \cos (φ)$

(48)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$Q_{3 ϕ} = \sqrt{3} . V_{ϕϕ} . I_{ϕϕ} . sen (φ)$

(49)

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como as relações entre tensão e corrente de linha e fase apresentadas na Tabela 2 são válidas para cargas equilibradas ligadas em qualquer ligação, as Equações 47, 48 e 49 são também aplicadas para cargas em triângulo.

Teoria na prática

Uma carga drena uma potência ativa de 5 Kw quando conectada a uma fonte de tensão de 120 volts. O fator de potência para essa condição é de 0,85. Determine o valor da potência reativa de um capacitor necessária para elevar o fator de potência para 0,95.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

O ângulo do fator de potência atual é dado por:

$c o s (θ_{1}) = 0,85 \to θ_{1} = 31,78 °$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A partir do fator de potência é possível calcular a potência aparente inicial:

$S_{1} = \frac{P}{f_{p}} = \frac{5.000}{0,85} = 5.882,3 V A$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A potência reativa é:

$Q_{1} = S_{1} s e n (θ_{1}) = 5.882,3 \times 0,52 = 3097,96 V A r$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para um fator de potência 0,95, o ângulo é:

$c o s (θ_{2}) = 0,95 \to θ_{2} = 18,19 °$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Na correção do fator de potência, a potência $P$ não muda, mas a potência aparente sim:

$S_{2} = \frac{P}{f_{p}} = \frac{5.000}{0,95} = 5.263,15 V A$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A nova potência reativa será:

$Q_{2} = S_{2} s e n (θ_{2}) = 1.642,94 V A r$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A diferença entre a potência reativa atual e a anterior é o valor do capacitor a ser inserido:

$Q_{c} = Q_{1} - Q_{2} = 3.097,96 - 1.642,94 = 1.455,6 V A r$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

RESOLUÇÃO

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

Conclusão

Considerações Finais

Neste tema, abordamos os principais conceitos relacionados à análise de circuitos em corrente alternada. Para isso, foram apresentadas as formas de representação dos elementos de circuito, fonte, resistor, capacitor e indutor, no domínio da frequência. Essa representação, denominada representação fasorial, permite avaliar a relação entre tensão e corrente desses elementos no domínio da frequência. Os métodos tradicionais de análise de circuitos foram apresentados para análise em CA.

Demonstramos ainda as relações de potência em corrente alternada, a partir dos conceitos de potência média e potência eficaz e fator de potência. Considerando a predominância dos circuitos CA para transmissão de energia, introduzimos as principais relações para circuitos trifásicos equilibrados, cujos elementos podem estar conectados em estrela ou triângulo. Por fim, apresentamos o conceito de potência complexa e potência trifásica.

Podcast

CONQUISTAS

Você atingiu os seguintes objetivos:

Lorem ipsum dolor sit amet, consectetur adipiscing elit

Ut enim ad minim veniam, quis nostrud exercitation ullamco

Duis aute irure dolor in reprehenderit in voluptate velit esse

Referências

ALEXANDER, C. K.; SADIKU, M. N. O. Fundamentos de circuitos elétricos. Porto Alegre: AMGH Editora, 2013.

BOYLESTAD, R. L.; NASCIMENTO, J. L. do. Introdução à análise de circuitos. São Paulo: Pearson Prentice Hall, 2004.

IRWIN, J. D. Análise de circuitos em engenharia. São Paulo: Pearson Education do Brasil, 2010.

JOHNSON, D. E.; HILBURN, J. L.; JOHNSON, J. R. Fundamentos de análise de circuitos elétricos. Rio de Janeiro: LTC, 1994.

NILSSON, J. W.; RIEDEL, S. A. Circuitos elétricos. 8. ed. São Paulo: Pearson Prentice Hall, 2008.

OLIVEIRA, C. C. B. et al. Introdução a sistemas elétricos de potência. Componentes simétricas. São Paulo: Blucher, 2000.

Explore+

Para saber mais sobre os assuntos tratados neste tema, leia:

ORSINI, L. Q.; CONSONNI, D. Curso de circuitos elétricos. 2. ed. São Paulo: Blucher, 2002.
ORSINI, L. Q.; CONSONNI, D. Curso de circuitos elétricos. v. II. 2. ed. São Paulo: Blucher, 2004.

Conteudista

Isabela Oliveira Guimarães

Currículo Lattes

Descrição

PROPÓSITO

Preparação

OBJETIVOS

Módulo 1

Módulo 2

Módulo 3

NOÇÕES SOBRE CORRENTE ALTERNADA SENOIDAL

MÓDULO 1

RELAÇÃO ENTRE TENSÃO E CORRENTE EM REGIME PERMANENTE SENOIDAL

RELAÇÃO ENTRE TENSÃO E CORRENTE

As tensões senoidais disponibilizadas para uso em residências, indústrias e aplicações em geral são originadas em geradores de CA.

Amcos (ωt+∅)

VPP=2VM

Amsen (α)

Exemplo

f=1T

Exemplo

v1t=10sen377t+30° V

v2(t)=5sen(377t-20°) V

f=ω2π=3772π=60 Hz

∅=30°--20°=50°

Valor médio de um sinal senoidal

O valor médio de um sinal senoidal é simplesmente a média desse sinal ao longo de um período.

Atenção

Valor eficaz (rms) de um sinal senoidal

Saiba mais

Arms=Am2

Comentário

Fasores

Fasores são vetores que giram em círculo no sentido anti-horário a dada velocidade angular constante.

Vt=Vmcosωt+θ

Número complexo

V=Vmejθ=Vm∠θ

Atenção

Relação de tensão e corrente para fasores

Resistores

Indutores

Capacitores

V=Ri

Vt=Vmcosωt+θ

it=Imcosωt+φ

Vmejθ=RImejφ

V=RI

Atenção

V(t) =Ldi(t)dt

Vmej(ωt + θ)=jωLImej(ωt + φ)

V=jωLI

it=CdV(t)dt

I=jωCV ⇒ V=IjωC

Teoria na prática

Vt=5cos20t+30° V

Vt=Vmcosωt+θ

V=Vmejθ=Vm∠θ

V=5ej30°=5∠30°

RESOLUÇÃO

Mão na Massa

Verificando o aprendizado

ATENÇÃO!

O conteúdo ainda não acabou.

Você chegou ao final do módulo 1!

MÓDULO 2

TÉCNICAS DE RESOLUÇÃO DE CIRCUITOS CA NO DOMÍNIO DA FREQUÊNCIA

Reatância indutiva e capacitiva

O comportamento de uma resistência tanto na corrente contínua (CC) quanto na corrente alternada (CA) é o mesmo. O resistor, quando submetido a uma corrente, dissipa calor através do efeito Joule.

Impedância do circuito

Tal relação normalmente resulta na expressão dos componentes do circuito como números complexos, o que será tratado como a impedância de cada elemento.

V=RI V=jωLI V=IjωC

VI=R VI=jωL VI=1jωC

R ⇒ Z=R

L ⇒ Z=jωL

C ⇒ Z=1jωC

Atenção

Z=R+jX

Você sabia

Z=R2+X2

θZ=tan-1XR

Exemplo

Z=10∠46,9°2∠10°=5∠36,9° Ω

Z=5cos46,9°+jcos10°

$A_{m} \cos (ω t + \emptyset)$

$V_{P P} = 2 V_{M}$

$A_{m} sen (α)$

$f = \frac{1}{T}$

$v_{1} (t) = 10 s e n (377 t + 30 °) V$

$v_{2} (t) = 5 s e n (377 t - 20 °) V$

$f = \frac{ω}{2 π} = \frac{377}{2 π} = 60 Hz$

$\emptyset = 30 ° - (- 20 °) = 50 °$

$A_{r m s} = \frac{A_{m}}{\sqrt{2}}$

$V (t) = V_{m} c o s (ω t + θ)$

$V = V_{m} e^{j θ} = V_{m} ∠ θ$

$V = Ri$

$V (t) = V_{m} \cos (ωt + θ)$

$i (t) = I_{m} \cos (ωt + φ)$

$V_{m} e^{j θ} = R I_{m} e^{j φ}$

$V = R I$

$V (t)$ $= L \frac{d i (t)}{d t}$

$V_{m} e^{j (ω t + θ)} = j ω L I_{m} e^{j (ω t + φ)}$

$V = j ω L I$

$i (t) = C \frac{d V (t)}{d t}$

$I = j ω C V \Rightarrow V = \frac{I}{j ω C}$

$V (t) = 5 c o s (20 t + 30 °) V$

$V (t) = V_{m} c o s (ω t + θ)$

$V = V_{m} e^{j θ} = V_{m} ∠ θ$

$V = 5 e^{j 30 °} = 5 ∠ 30 °$

$V = R I V = j ω L I V = \frac{I}{j ω C}$

$\frac{V}{I} = R \frac{V}{I} = j ω L \frac{V}{I} = \frac{1}{j ω C}$

$R \Rightarrow Z = R$

$L \Rightarrow Z = j ω L$

$C \Rightarrow Z = \frac{1}{j ω C}$

$Z = R + j X$

$|Z| = \sqrt{R^{2} + X^{2}}$

$θ_{Z} = t a n^{- 1} \frac{X}{R}$

$Z = \frac{10 ∠ 46,9 °}{2 ∠ 10 °} = 5 ∠ 36,9 ° Ω$

$Z = 5 (\cos 46,9 ° + jcos 10 °)$

$Z = 4 + j 3 Ω$

$Y = \frac{1}{Z}$

$Y = G + j B$

$G + j B = \frac{1}{R + j X}$

$G = \frac{R}{R^{2} + X^{2}} B = - \frac{X}{R^{2} + X^{2}}$

$V_{1} + V_{2} + \dots + V_{n} = 0$

$V_{n} = V_{n} ∠ θ_{n}, n = 1,2, 3, \dots . . n$

$I_{1} + I_{2} + \dots + I_{n} = 0$

$I_{n} = I_{n} ∠ θ_{n}, n = 1,2, 3, \dots . . n$

$V_{1} = Z_{1} I, V_{2} = Z_{2} I, V_{3} = Z_{3} I, \dots, V_{n} = Z_{n} I$

$V = V_{1} + V_{2} + \dots + V_{n}$

$V = (Z_{1} + Z_{2} + \dots + Z_{n}) I = 0$

$V = Z_{eq} I$

$Z_{e q} = Z_{1} + Z_{2} + \dots + Z_{n}$

$I = I_{1} + I_{2} + \dots + I_{n}$

$I = V (\frac{1}{Z_{1}} + \frac{1}{Z_{2}} + \dots + \frac{1}{Z_{n}})$

$\frac{1}{Z_{e q}} = \frac{I}{V} = \frac{1}{Z_{1}} + \frac{1}{Z_{2}} + \dots + \frac{1}{Z_{n}}$

$Y_{e q} = Y_{1} + Y_{2} + \dots + Y_{n}$

$V_{1} = Z_{1} I$

$V_{2} = Z_{2} I$

$V_{1} = \frac{Z_{1}}{Z_{1} + Z_{2}} V V_{2} = \frac{Z_{2}}{Z_{1} + Z_{2}} V$

$\frac{V_{1} - 5 ∠ 0 °}{0,5} + \frac{V_{1}}{- j 1} + \frac{V_{1} - V_{2}}{- j 1} = 0$

$(2 + j 2) V_{1} - j V_{2} = 10$

$\frac{V_{2} - V_{1}}{- j 1} + \frac{V_{2}}{0,2 + j 0,4} = 5 ∠ 0 °$

$- j V_{1} + (1 - j) V_{2} = 5$

$[\begin{matrix} 2 + j 2 & - j \\ - j & 1 - j \end{matrix}] [\begin{matrix} V_{1} \\ V_{2} \end{matrix}] = [\begin{matrix} 10 \\ 5 \end{matrix}]$

$V_{1} = 2 - j = 2,23 ∠ - 26,6 ° V$

$V_{2} = 2 + j 4 = 4,47 ∠ 63,4 ° V$

$- 10 ∠ 0 ° - j 6 I_{1} + j 3 (I_{1} - I_{2}) = 0$

$- j 3 I_{1} - j 3 I_{2} = 10 ∠ 0 °$

$j 3 (I_{2} - I_{1}) + 2 I_{2} + 16 ∠ 0 ° = 0$

$- j 3 I_{1} + (2 + j 3) I_{2} = - 16 ∠ 0 °$

$[\begin{matrix} - j 3 & - j 3 \\ - j 3 & 2 + j 3 \end{matrix}] [\begin{matrix} I_{1} \\ I_{2} \end{matrix}] = [\begin{matrix} 10 \\ - 16 \end{matrix}]$

$I_{1} = 1,7 ∠ - 23,5 ° A$

$I_{2} = 7,1 ∠ 108 ° A$

$Z_{t h} = 1 + (- j 1) = 1 - j 1 Ω$

$V_{1} = 2 . 1 = 2 V$

$V_{t h} = V_{1} - (- j 1) 2 V_{1} = 2 (1 + j 2) = 2 + j 4 V$

A potência instantânea $P (t)$ de um circuito é o produto da tensão instantânea $V (t)$ com a corrente instantânea $I (t)$ , sendo medida em watts (W)

$P (t) = V (t) i (t)$