Descrição
A caracterização e a modelagem dos elementos reativos que compõem os circuitos, desde a representação do componente, a análise do funcionamento dos mesmos, bem como as principais técnicas para simplificação durante a avaliação.
PROPÓSITO
Compreender as características e funcionalidades dos elementos passivos de um circuito elétrico, uma vez que estes estão presentes em diversos equipamentos elétricos, eletrônicos e mecatrônicos.
Preparação
Antes de iniciar o estudo, tenha em mãos uma calculadora para executar os cálculos dos exercícios propostos.
OBJETIVOS
Módulo 1
Descrever o elemento indutor
Módulo 2
Empregar o elemento capacitor
Módulo 3
Identificar as formas de onda dos elementos passivos
INDUTORES E CAPACITORES
MÓDULO 1
Descrever o elemento indutor
ELEMENTO INDUTOR
Indutores
Os circuitos elétricos são compostos por diversos elementos, fontes, resistores e outros.
Entre os elementos que compõem o circuito elétrico, encontramos os ativos e os passivos.
O indutor é um elemento passivo, cuja função principal, responsável por sua característica comportamental, é armazenar energia na forma de campo magnético. Esses componentes podem ser utilizados em diversas áreas, tanto em sistemas de potência quanto em eletrônica. Usualmente os indutores são encontrados em fontes de tensão, nos transformadores e em motores elétricos.
Exemplo
Um condutor de corrente pode ser considerado um indutor por apresentar propriedades indutivas.
A construção de um indutor é feita, em geral, utilizando-se diversas espiras enroladas de material condutor (a exemplo do cobre) na forma de uma bobina. Esse aspecto construtivo confere a potencialização do efeito indutivo.
Você sabia
É possível descrever um indutor como uma bobina composta por um fio condutor.
Quando uma corrente elétrica percorre esse elemento, pode-se observar que há uma proporção entre a variação dessa corrente elétrica e a tensão sobre o componente. É possível descrever matematicamente esse comportamento pela Equação 1 seguinte:
$$v=L\frac{di}{dt}$$
(1)
Na qual:
- $$v$$ é tensão sob o indutor;
- $$i$$ é a corrente que circula por ele;
- $$L$$ é a indutância, que descreve a proporcionalidade entre a tensão e a variação da corrente. Esse valor é medido em Henry (H).
É importante destacar alguns dados:
A tensão em um indutor é nula, quando não há variação de corrente no tempo, ou seja, em casos em que a corrente é contínua. Isso equivale a um curto-circuito.
A indutância é uma propriedade característica do indutor e, a partir desta, o indutor se opõe a variação do fluxo de corrente que o atravessa.
Um indutor se opõe à passagem de corrente; dessa forma, este valor não pode mudar de forma instantânea.
A indutância é uma característica do componente que varia com as dimensões físicas do indutor, isto é, de acordo com os aspectos construtivos. Essa variação pode ser representada pela Equação 2:
$$L=\frac{N^2\mu A}{l}$$
(2)
Na qual:
- $$N$$ é o número de espiras;
- $$A$$ é a área da seção transversal;
- $$\mu$$ é a permeabilidade do material
- $$l$$ é o comprimento da bobina.
- Utilizar materiais que apresentem elevada permeabilidade.
- Alterar o número de espiras do indutor, aumentando-as.
- Aumentar a área da secção transversal.
- Reduzir o comprimento.
Analisando a Equação 2, notamos que, para obter uma elevada indutância, podemos fazer as seguintes alterações:
Atenção
Essa equação é válida somente para indutores com formato solenoide. Para as demais geometrias é necessário avaliar matematicamente usando técnicas e cálculos que envolvem as teorias do eletromagnetismo.
Saiba mais
O mercado oferece diversos tipos (modelos e tamanhos) de indutor e dos mais variados valores; os mais comuns na faixa de µH até poucos H, podendo ter valores fixos ou variáveis. Quanto ao aspecto construtivo do núcleo, os materiais mais comuns são plásticos, ferro, aço ou ar.
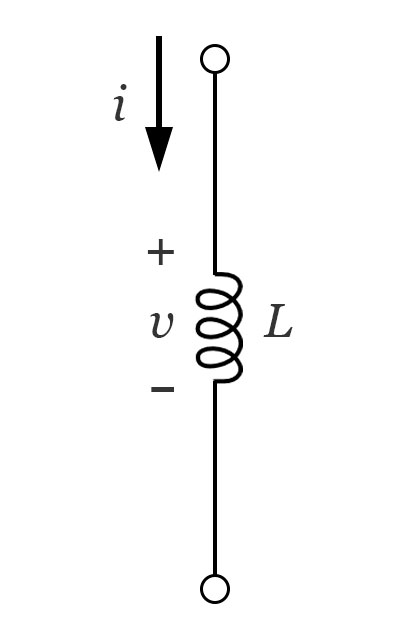
A representação gráfica de um indutor é feita através do símbolo na figura abaixo, podendo haver algumas variações nesta representação de acordo com o tipo de material que compõe o núcleo do indutor (ar, ferro, plastico, etc.).
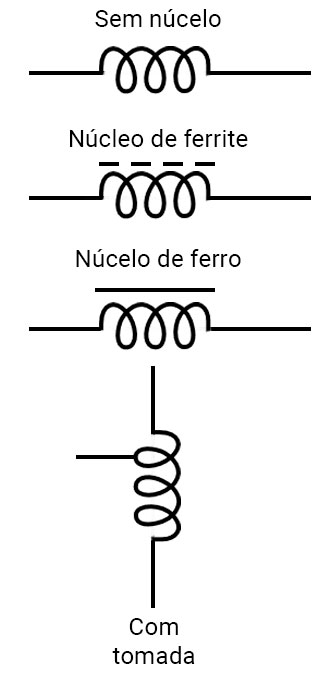
Saiba mais
Exemplos de diferentes representações de indutores em função do aspecto construtivo do núcleo.
Um indutor que possui indutância independente da corrente é conhecido por sua característica linear, cujo comportamento gráfico pode ser dado por uma linha reta.
Para este estudo, consideramos que os indutores são de natureza linear, em que a relação entre tensão e corrente foi apresentada na Equação 1. Integrando essa mesma equação, obtemos a seguinte expressão:
$$i=\frac{1}{L}\int_{t_0}^{t}v\left(t\right)dt+i(t_0)$$
(3)
Na qual:
- $$i(t_0)$$ representa a corrente total quando t varia entre $$-\infty$$ até $$t_0$$.
Cálculo da potência
O indutor é caracterizado por armazenar energia em seu campo magnético. Assim, é possível e desejável que esse valor referente à energia seja calculado. Sabe-se que a equação que expressa a potência em um componente parte da relação entre tensão e corrente, que é representada a seguir:
$$p=vi$$
(4)
Substituindo o valor de tensão (v) pelo valor da tensão calculada para o indutor, obtém-se a Equação 5:
$$p=\left(L\frac{di}{dt}\right)i\ $$
(5)
Energia armazenada
Como o intuito é o cálculo da energia armazenada, é necessário integrar a potência encontrada anteriormente, variando-a temporalmente. Tem-se, portanto, a seguinte análise:
$$w=\int_{-\infty}^{t}p\left(t\right)dt$$
(6)
$$w=\int_{-\infty}^{t}{\left(L\frac{di}{dt}\right)i\ dt}$$
(7)
$$w=\int_{-\infty}^t\left(L\frac{di}{dt}\right)i\;dt\;=\;L\;\int_{-\infty}^t\;(di)i$$
(8)
$$w=L\int_{-\infty}^{t}{\left(di\right)i\ }=\frac{{Li}^2(t)}{2}-\frac{{Li}^2(-\infty)}{2}$$
(9)
Na qual:
- $$i\left(-\infty\right)=0$$
A energia armazenada em um indutor é dada pela seguinte equação:
$$w=\frac{{Li}^2}{2}$$
(10)
A energia armazenada no indutor não é dissipada, como ocorre, por exemplo, com os resistores (elementos ativos). A energia é liberada para o circuito e pode ser recuperada posteriormente.
Indutores reais, todavia, possuem um componente resistivo, cujo valor pode variar. Através desse componente resistivo pode haver dissipação da energia armazenada, devido ao Efeito Joule.
Comentário
Para fins deste estudo, estaremos considerando os indutores como ideais, o que implica desconsiderar as eventuais perdas de energia a partir do Efeito Joule.
Atenção
Pelo Sistema Internacional de Medidas (SI), a energia é medida em Joules (J).
Associação de indutores
Para trabalhar de forma adequada com o indutor, é preciso entender como executar as associações “em série” e “em paralelo”. De acordo com a configuração do circuito, o ideal é encontrar um valor de indutância que represente o equivalente dos indutores presentes, o que possibilita a simplificação do circuito tornando mais fácil a análise da composição final. Dessa forma, temos duas possibilidades para avaliar as disposições dos componentes, em série e em paralelo.
Indutores em série
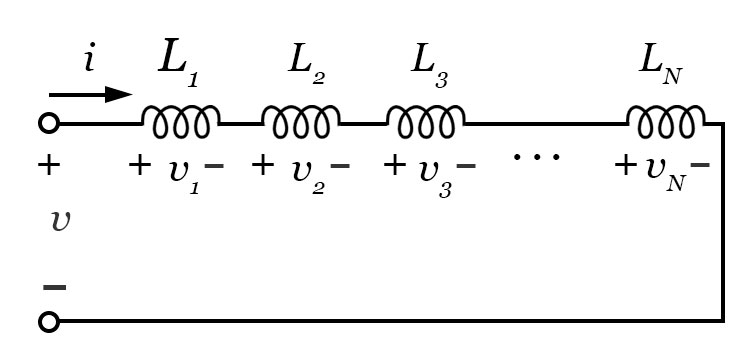
Como exemplo, considere um circuito com diversos indutores conectados em série, como mostra a imagem ao lado. Cada indutor possui um valor de tensão que, pela lei de Kirchhoff das Tensões (LKT), pode ser descrito pela equação 11:
$$v-v_2-v_3-\ldots v_N=0$$
(11)
A tensão no indutor pode ser substituída pela equação apresentada anteriormente, guiando o seguinte modelo:
$$v=L_1\frac{di}{dt}+L_2\frac{di}{dt}+L_3\frac{di}{dt}+\ldots+L_N\frac{di}{dt}$$
(12)
$$v=(L_1+L_2+L_3+\ldots+L_N)\frac{di}{dt}$$
(13)
$$L_{eq}=(L_1+L_2+L_3+\ldots+L_N)$$
(14)
Na qual:
- $$L_{eq}$$ representa a indutância equivalente do circuito série.
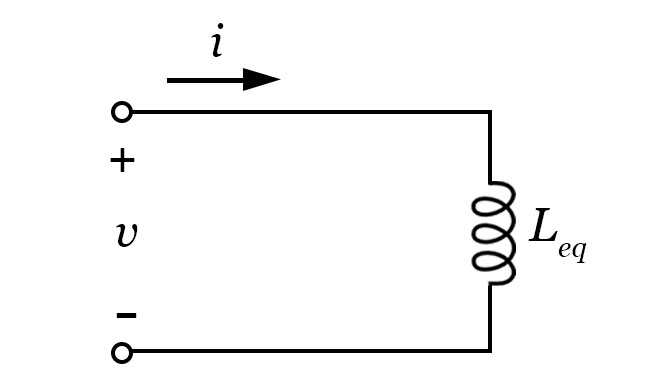
Indutores em paralelo
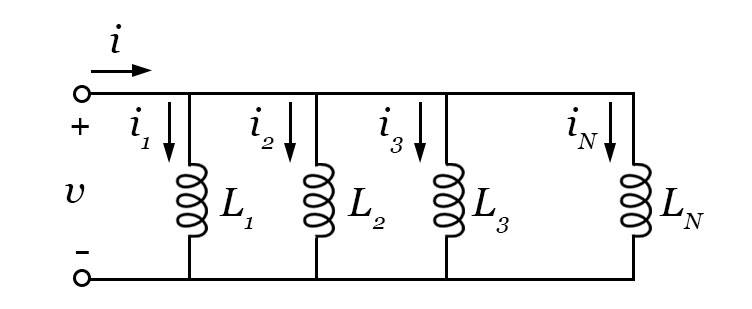
Considerando agora o circuito apresentado na imagem ao lado, cujos indutores são conectados em paralelo, deve-se aplicar a Lei de Kirchhoff das Correntes (LKC) para a análise. Dessa forma, tem-se a seguinte equação para o nó:
$$i-i_1-i_2-\ldots i_N=0$$
(15)
Obtemos a corrente no indutor integrando a equação:
$$i=\frac{1}{L}\int_{t_0}^{t}vdt+i(t_0)0$$
(16)
Como em um sistema paralelo, a tensão em um nó é igual para todos os ramos conectados a ele, enquanto as correntes se diferem. Podemos reescrever a equação da seguinte forma:
$$i=\frac{1}{L_1}\int_{t_0}^{t}vdt+i_1\left(t_0\right)+\frac{1}{L_2}\int_{t_0}^{t}vdt+i_2\left(t_0\right)+\frac{1}{L_3}\int_{t_0}^{t}vdt+i_3\left(t_0\right)+\ldots+\frac{1}{L_N}\int_{t_0}^{t}vdt+i_N(t_0)$$
(17)
Assim, rearranjando a expressão, tem-se:
$$i=\left(\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}+\ldots+\frac{1}{L_N}\right)\int_{t_0}^{t}vdt+i_1\left(t_0\right){+i}_2\left(t_0\right)+i_3\left(t_0\right)+\ldots+i_N(t_0)$$
(18)
Na qual é possível visualizar o valor equivalente da indutância por meio da equação a seguir:
$$\frac{1}{L_{eq}}=\left(\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}+\ldots+\frac{1}{L_N}\right)$$
(19)
Os valores definidos por $$i_1\left(t_0\right)$$ e demais referem-se aos valores iniciais de corrente que circulam no indutor.
Atenção
A associação entre indutores é realizada da mesma forma que a associação entre resistores. Isto é valido tanto para associações em série quanto em paralelo.
Exemplo comentado
Apresentamos, a seguir, um exercício comentado no intuito de aplicar as equações propostas neste módulo.
$$i\left(t\right)=5te^{-t}A$$
Encontre a tensão nos terminais do indutor, bem como a energia armazenada.
Como já vimos, a tensão em um indutor é dada pela seguinte expressão:
$$v=L\frac{di}{dt}$$
Dessa forma, é necessário derivar a corrente conhecida em função do tempo. Assim:
$$v=(0,2)\frac{d(5te^{-t})}{dt}$$
Sendo:
$$v=\left(0,2\right)\left[\left(5\right)e^{-t}-5te^{-t}\right]\ V$$
$$v=\left(e^{-t}-te^{-t}\right)\ V$$
$$v=e^{-t}\left(1-t\right)\ V$$
A energia armazenada no indutor, por sua vez, é dada pela seguinte equação:
$$w=\frac{{Li}^2}{2}$$
Substituindo os valores, tem-se:
$$w=\frac{{(0,2)(5te^{-t})}^2}{2}$$
$$w=\frac{0,2(25t^2e^{-2t})}{2}$$
$$w=2,5t^2e^{-2t}\ \ J$$
Tipos de indutores
De uma forma geral, os indutores podem ser construídos pela utilização de uma bobina e um material condutor. Já o material que compõe o núcleo da bobina tem a função de garantir a concentração das linhas de fluxo magnético, reduzindo as perdas. Isto confere maior grau de indutância ao indutor.
Os indutores têm aplicação em diversas áreas. Por essa razão, existem variedades quanto à geometria e seus aspectos construtivos para atender cenários particulares.
Exemplo
Indutores menores são utilizados em aplicações que requerem elevada frequência.
Há também diversos materiais aplicados ao núcleo no intuito de variar a indutância, como veremos a seguir:
São utilizados em cenários onde a elevada indutância é requerida, como por exemplo, nos circuitos integrados (os mesmos utilizados na construção de chips de computador). O material ferromagnético é caracterizado pela capacidade de concentrar as linhas de fluxo.
Indutor de núcleo laminado
Um núcleo dito laminado é construído por camadas de material (de baixa espessura e disposto um sobre o outro). Essa construção laminada reduz as perdas no componente. É amplamente usado em aplicações de baixas frequências (sistemas de potência, construção de transformadores).
Indutor de núcleo de ar
Tem o ar como composição do núcleo, ou seja, não há utilização de nenhum outro material. Neste caso, a indutância é baixa, contudo, a ausência de um material na composição do núcleo faz com que as perdas não ocorram. São componentes utilizados em alta frequência, como emissores e receptores.
Indutor com núcleo de ferrite
O material que compõe o núcleo deste indutor promove a redução das perdas. É aplicado em projetos em que se requer alta frequência, como em moduladores de frequência.
Indutor toroidal
Utiliza a ferrite como material que compõe o núcleo, conforme o tipo anterior. Porém possui formato de rosca, fazendo com que a circulação do fluxo se dê em um caminho fechado. A vantagem promovida por este componente reside na redução das perdas e no aumento no valor da indutância. Este componente é utilizado em placas integradas de computadores.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 2
Empregar o elemento capacitor
ELEMENTO CAPACITOR
Capacitores
Tal como os indutores, os capacitores são componentes passivos capazes de armazenar energia sob a forma de campo elétrico. São constituídos de duas superfícies condutoras que são separadas por um material não condutor (isolante) ou dielétrico (dessa forma não há contato entre os terminais).
Exemplo
A superfície condutora pode ser de diversos materiais como, alumínio, cerâmica, tântalo, poliéster etc. O que também se aplica ao dielétrico, onde podem ser encontrados elementos como ar, papel etc.
O funcionamento do capacitor se dá quando ele é conectado a uma fonte de tensão. Neste momento, as superfícies condutoras recebem cargas positivas e negativas tornando-se polarizadas.
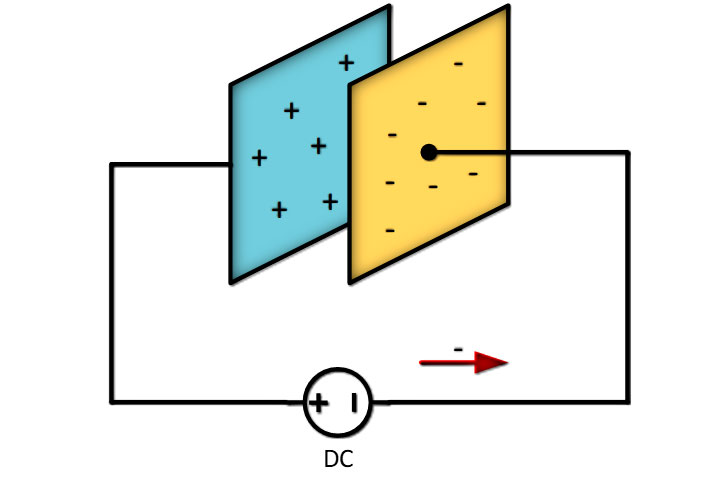
O capacitor armazena a carga depositada, que é proporcional à tensão da fonte, modelada pela equação:
$$q=Cv$$
(1)
Na qual:
- $$q$$ representa a carga armazenada;
- $$C$$ representa a capacitância em farad (F);
- $$v$$ representa a tensão aplicada.
Ou, ainda, a capacitância é descrita pela razão entre a quantidade de carga encontrada nas placas e a tensão aplicada:
$$C=\frac{q}{v}$$
(2)
É importante ressaltar que a capacitância, bem como a indutância, depende da geometria do material. E, para um capacitor de placas paralelas, esta pode ser descrita pela equação:
$$C=\frac{\varepsilon A}{d}$$
(3)
Na qual:
- $$\varepsilon$$ representa a permissividade do material dielétrico, responsável por separar as placas condutoras;
- $$A$$ representa a área de cada placa;
- $$d$$ representa a distância entre as placas condutoras.
Avaliando cada variável que compõe a capacitância, pode-se concluir que, para aumentar esse valor, é necessário aplicar as alterações apresentadas a seguir:
- Reduzir a distância entre as placas, $$d$$;
- Aumentar a área das placas, $$A$$;
- Utilizar materiais de maior permissividade, $$\varepsilon$$
Quanto à parte comercial, os valores referentes aos capacitores podem variar de pF (picofarads) à µF (microfarads), caracterizados pela composição do material construtivo do dielétrico. Podem ainda ser de valores fixos ou variáveis, como ocorre com indutores e resistores. São encontrados como mostra a imagem abaixo:
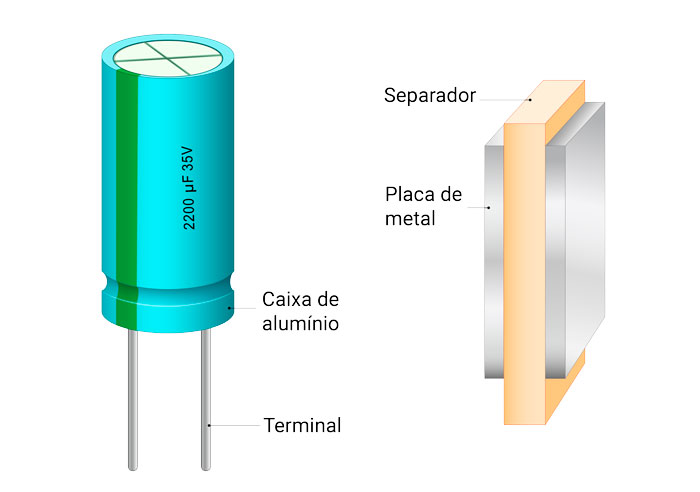
Atenção
Para um capacitor, atenta-se à convenção de sinais:
- $$v\;,\;i\;>\;0$$: o capacitor está em carregamento.
- $$v\;,\;i\;<\;0$$: o capacitor está descarregando.
Relação corrente-tensão
Como visto na equação $$C=\frac{q}{V}$$, é possível descrever a quantidade de carga armazenada pelo capacitor relacionando a capacitância e a tensão aplicada. Sabe-se que a corrente elétrica pode ser representada pela variação de cargas que atravessa o condutor em determinado instante de tempo, Equação 4:
$$i=\frac{dq}{dt}$$
(4)
Relacionando as Equações 2 e 4, e derivando a equação dos dois lados, é possível obter a Equação 5, que representa a corrente que circula pelo capacitor. Esta é válida para componentes lineares. Quando este possui características não lineares, não é possível descrever corrente e tensão por uma reta.
$$i=C\frac{dv}{dt}$$
(5)
Integrando a Equação 5, é possível obter a tensão em um capacitor, que é descrita pela Equação 6 apresentada a seguir:
$$v\left(t\right)=\frac{1}{C}\int_{-\infty}^{t}i\left(t\right)dt$$
(6)
Ou, ainda, pode-se descrever a tensão pela Equação 7, onde se observa que a tensão depende da variação da corrente no tempo, destacando assim a propriedade conhecida como memória do elemento.
$$v\left(t\right)=\frac{1}{C}\int_{-\infty}^{t}i\left(t\right)dt$$
(7)
Em que $$v(t_0)$$ descreve a tensão inicial no elemento, que pode ainda ser representada pela Equação 8.
$$v(t_0)\ =\frac{q(t_0)}{C}$$
(8)
Dadas as equações, é possível concluir:
Não havendo variação de tensão com o tempo, a corrente no capacitor é nula. Isso se aplica em tensões contínuas. Assim, para um circuito CC, o capacitor se comporta como um circuito aberto, não havendo circulação de corrente. Porém, a conexão de uma fonte nos terminais desse componente faz com que ele se carregue.
A tensão no capacitor deve ser contínua, isto é, não pode mudar de forma abrupta, como ocorre com a corrente que circula pelo indutor. Assim, o capacitor tem a característica de resistir à mudança de tensão nos terminais. Essa alteração faz com que seja necessária uma corrente muito elevada (infinita), tornando-se impraticável.
A corrente no capacitor, diferente da tensão, pode mudar de forma instantânea.
A energia armazenada no capacitor circula no circuito, ou seja, inicialmente o componente armazena energia e esta é liberada sob a forma de potência para o circuito, sem que haja dissipação, considerando capacitores ideais. Na prática, há um componente resistivo conhecido por resistência de fuga.
Associação de capacitores
Assim como os demais componentes aqui tratados, os capacitores podem ser associados para que haja redução do circuito durante a análise. Esta associação ocorre de duas formas, em série ou em paralelo, proporcionando encontrar um capacitor equivalente que represente a junção dos demais.
Capacitores em série
Para analisar uma associação de capacitores conectados em série, considere o circuito apresentado na imagem. Como vimos, em um circuito em série a corrente circulante é igual em todos os componentes, contudo a tensão se distingue.
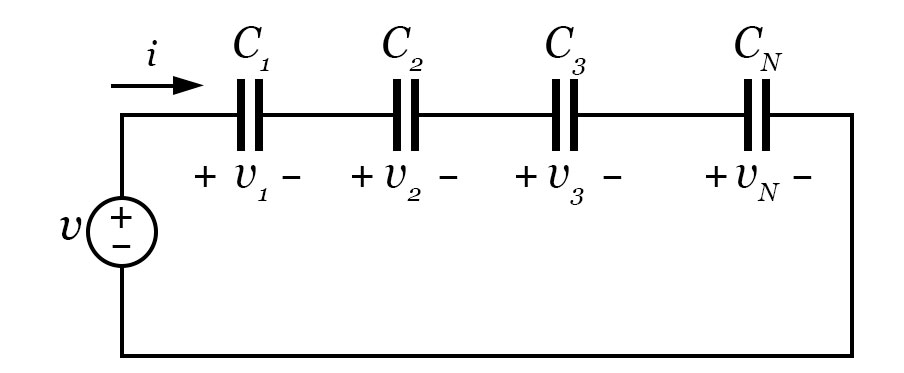
Para avaliar o valor equivalente da capacitância, aplica-se a LKC, e partindo desta obtém-se a seguinte equação:
$$v-v_1+v_2+v_3+\ldots+v_N=0$$
(9)
Pela integração do valor da corrente que circula no capacitor, é possível obter a tensão sobre ele, como mostra a equação. Assim, ao substituir esse valor na Equação 9 anterior, resulta o seguinte modelo na Equação 10:
$$v=\frac{1}{C_1}\int_{t_0}^{t}{i(t)}dt+v_1\left(t_0\right)+\frac{1}{C_2}\int_{t_0}^{t}{i(t)}dt+v_2\left(t_0\right)+\frac{1}{C_3}\int_{t_0}^{t}{i(t)}dt+v_3\left(t_0\right)+\ldots+\frac{1}{C_N}\int_{t_0}^{t}{i(t)}dt+v_N(t_0)$$
(10)
Reorganizando a Equação 10, é obtida a Equação 11:
$$v=\left(\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots+\frac{1}{C_N}\right)\int_{t_0}^{t}i\left(t\right)dt+v_1\left(t_0\right)+v_2\left(t_0\right)+v_3\left(t_0\right)+\ldots v_N(t_0)$$
(11)
Em que, por simplificação, tem-se:
$$\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots+\frac{1}{C_N}$$
(12)
Na qual:
- $$C_{eq}$$ é a capacitância equivalente;
- $$v_1\left(t_0\right)+v_2\left(t_0\right)+v_3\left(t_0\right)+\ldots v_N(t_0)$$ é a soma dos valores inicialmente armazenados pelo componente.
Capacitor em paralelo
Para analisar uma associação de capacitores conectados em paralelo, considere a seguinte imagem.
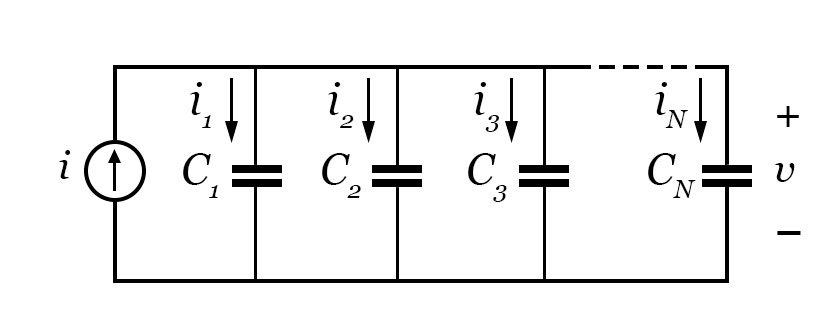
Partindo do circuito apresentado, aplica-se a LKC. Sabe-se que, em um circuito paralelo, as tensões em um nó são iguais para os ramos conectados a ele. As correntes, no entanto, diferem. Assim, é possível obter a seguinte equação:
$$i-i_1+i_2+i_3+\ldots+i_N=0$$
(13)
Conhecendo a equação que descreve a corrente que circula pelo capacitor e substituindo-a na equação acima, obtém-se a relação apresentada pela equação a seguir:
$$i=C_1\frac{dv}{dt}+C_2\frac{dv}{dt}+C_3\frac{dv}{dt}+\ldots+C_N\frac{dv}{dt}$$
(14)
Em que, após o rearranjo da expressão, são obtidas a Equação 15 e a simplificação apresentada pela Equação 16:
$$i=(C_1+C_2+C_3+\ldots+C_N)\frac{dv}{dt}$$
(15)
$$C_{eq}=(C_1+C_2+C_3+\ldots+C_N)$$
(16)
Na qual:
$$C_{eq}$$ é a capacitância equivalente do circuito paralelo.
Atenção
A associação das capacitâncias em série se dá da mesma forma que a associação das indutâncias e resistências em paralelo. De forma análoga, as capacitâncias em paralelo são obtidas por meio da soma dos valores individuais, como ocorre nas associações em série para indutores e resistores.
Potência e energia
Para calcular a potência instantânea em um capacitor, inicia-se pela relação básica entre a tensão e a corrente medidas em um elemento, como mostra a equação a seguir:
$$p=vi$$
(17)
Substituindo o valor de corrente pela Equação 5, referente à corrente que circula em um capacitor, obtém-se a potência liberada para ele, apresentada pela próxima equação:
$$p=C\frac{dv}{dt}$$
(18)
Partindo da Equação 18 e considerando as propriedades do elemento, caracterizado pelo armazenamento de energia, é desejável calcular a quantidade de energia armazenada em seu campo elétrico. Para isso, basta integrar (temporalmente) o valor referente à potência calculada. Assim, tem-se a seguinte expressão:
$$w=\int_{-\infty}^{t}p\left(t\right)dt$$
Onde, ao substituir a variável ‘p’ pela expressão de potência encontrada, são obtidas as Equações 19 e 20:
$$w=C\int_{-\infty}^{t}{v\frac{dv}{dt}dt}=C\int_{v(-\infty)}^{v(t)}vdv$$
(19)
$$w=C\frac{1}{2}{v^2|}_{v(-\infty)}^{v(t)}$$
(20)
Por observação, é possível concluir:
Em $$v(-\infty)$$, o capacitor está descarregado; dessa forma, a energia armazenada pode ser representada como segue:
$$w=C\frac{1}{2}v^2$$
(21)
Essa energia é armazenada do campo elétrico que existe entre as superfícies condutoras do capacitor.
Como o capacitor não é capaz de dissipar energia como ocorre com resistor, essa energia circula no circuito, podendo ser recuperada. Em capacitores reais, é possível observar que uma componente resistiva, ainda que baixa, promove dissipação.
Exemplos Comentados
Apresentamos alguns exercícios comentados no intuito de aplicar as equações propostas neste módulo e ajudar você a entender bem do conteúdo.
1. Considere um capacitor de 4pF para os seguintes cálculos:
a) Determinar carga armazenada, considerando que há uma fonte de 20 V entre seus terminais.
Utilizar a seguinte equação:
$$C=\frac{q}{v}$$
Isolar a variável carga, ao qual desejamos calcular:
$$q=Cv$$
Assim, substituir os valores de C e v:
$$q=4\ast{10}^{-12}\ast20=80pF$$
b) Determinar a energia armazenada neste capacitor..
Para determinar a energia armazenada, tem-se a seguinte equação:
$$w=C\frac{1}{2}v^2$$
De posse dos valores de capacitância e tensão, tem-se:
$$w=\frac{1}{2}(4\ast{10}^{-12})(20^2)=800\ pJ$$
2. Considere um capacitor de 4µF, cuja tensão em seus terminais é dada pela seguinte expressão:
$$v\left(t\right)=5\cos{\left(6000t\right)}V$$
Para esse capacitor, pede-se a corrente que circula por ele.
Por definição, a corrente que circula pelo capacitor é dada por:
$$i\left(t\right)=C\frac{dv}{dt}$$
Substituir os valores na equação:
$$i\left(t\right)=C\frac{dv}{dt}=(4\ast{10}^{-6})\frac{d(5\cos{\left(6000t\right)})}{dt}$$
$$i\left(t\right)=C\frac{dv}{dt}=(4\ast{10}^{-6})(5)(-sen\left(6000t\right))(6000)$$
$$i\left(t\right)=-0,12sen\left(6000t\right)A$$
3. Para o circuito apresentado a seguir, pede-se a capacitância equivalente:
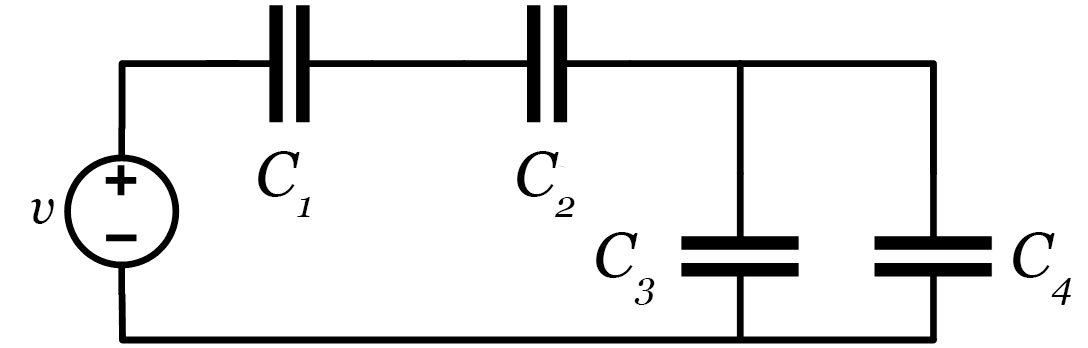
Para avaliar esse problema, é necessário dividi-lo em suas partes:
- Associação em paralelo
- Associação em série
A associação em paralelo é composta dos capacitores C3 e C4. Por definição, esta pode ser solucionada da seguinte forma:
$$C_{eq}={(C}_1+C_2+C_3+\ldots+C_N)$$
Assim, tem-se uma capacitância equivalente dada por:
$$C_{eq}={(C}_3+C_4)=C_5$$
Este resultante encontra-se em paralelo com C1 e C2 que, por definição, pode ser dado pela seguinte associação:
$$\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots+\frac{1}{C_N}$$
Assim, tem-se:
$$C_{eq}=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_5}}$$
Que traduz a capacitância equivalente desse circuito.
Considere agora os valores para as seguintes capacitâncias do circuito:
$$C_1=20mF$$
$$C_2=30mF$$
$$C_3=40mF$$
$$C_4=20mF$$
a) Defina o valor da capacitância total equivalente.
Utilizando das equações já encontradas, sabe-se que a capacitância C5, que representa o equivalente série, é dada por:
$$C_{eq}={(C}_3+C_4)=C_5=60mF$$
$$(40+20)m=C_5=60mF$$
Por sua vez, esse valor é associado em série com as demais, onde tem-se:
$$C_{eq}=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_5}}$$
Assim:
$$C_{eq}=\frac{1}{\frac{1}{60}+\frac{1}{30}+\frac{1}{20}}m=10mF$$
b) Considere que a fonte “v” é de 20V, calcule a carga total desse circuito:
Sabe-se que:
$$q=Cv$$
Dessa forma, basta que os valores sejam substituídos na equação acima:
$$q=\left(10m\right)\left(20\right)=0,2C$$
Tipos de capacitores
Assim como os indutores, os capacitores podem ser encontrados sob diversas geometrias e variações no material isolante (dielétrico), que caracteriza o tipo de aplicação a ser feita. Contudo, isso não altera sua função, que é o armazenamento de energia.
Vejamos alguns tipos de capacitores e suas características construtivas:
Caracterizado por apresentar um dielétrico, ou isolante, de pequena espessura — isto ao ser comparado aos demais modelos. É formado por duas folhas de alumínio, que são separadas por uma camada de óxido de alumínio. É importante ressaltar que este componente possui polaridade, isso significa que há uma forma adequada de instalá-lo em um circuito. Para identificar, basta que localize o terminal maior (o positivo). Em muitos casos, pode ser observada uma identificação de terminais referenciando os dois polos. A aplicação do capacitor eletrolítico pode ser feita em fontes de tensão, por exemplo, com o intuito de manter a tensão estável e filtrando possíveis ruídos.
Atenção
Se este capacitor for polarizado de forma incorreta, isto é, utilizado de maneira inversa, ele entra em curto-circuito, o que pode ser um problema, uma vez que tende a ocorrer uma explosão (modelos mais antigos) e liberar gases.
É um modelo a ser utilizado na substituição do eletrolítico (já apresentado) quando for desejável a redução do circuito. A composição do isolante é feita por óxido de tântalo, que se caracteriza por apresentar uma vida útil mais longa que os eletrolíticos. Esses capacitores estão substituindo os de alumínio em todos os tipos de circuitos em razão de seu baixo volume.
Atenção
O capacitor de tântalo requer polarização correta, pois se for utilizado de maneira inversa pode explodir. Em muitos casos, a polarização é indicada no próprio capacitor, no intuito de evitar acidentes (o terminal positivo é o maior).
Formado por camadas de poliéster e alumínio, a quantidade de folhas e suas espessuras se tornam responsáveis por definir a capacitância do capacitor. É um modelo compacto e caracterizado por ser capaz de autorregeneração. Por exemplo, em situações em que há danos entre as camadas do poliéster, geradas por sobretensão, o material que se encontra sobre a folha é capaz de evaporar e evitar o curto-circuito.
Este modelo é um dos mais largamente utilizados. Seu aspecto construtivo se dá por um disco de cerâmica, compondo a parte isolante, e por duas fitas metálicas encontradas nas faces (uma em cada lado). O capacitor cerâmico não é capaz de armazenar grandes quantidades de carga. Em geral, sua aplicação é feita nos circuitos de alta frequência e corrente contínua, como por exemplo em televisões, rádios, flashes de câmeras, roteadores e demais eletrônicos.
O aspecto construtivo deste capacitor é dado pela aplicação da mica como dielétrico e o uso de placas de prata que envolvem o dielétrico. É um componente considerado estável e não apresenta elevados valores de perda de carga. Suas aplicações englobam circuitos osciladores e circuitos ressonantes.
Atenção
Os capacitores de mica podem ou não possuir terminais. Em alguns casos, estes são soldados na própria placa do circuito promovendo boa dissipação de calor.
O material que compõe o dielétrico deste modelo de capacitor pode variar (por exemplo, cerâmica, tântalo). São componentes pequenos e por isso suas aplicações são voltadas para equipamentos eletrônicos de uma forma geral e para circuitos de robótica.
É composto por placas que podem ser de alumínio ou latão. Geralmente, o material isolante é composto de ar. O valor dos capacitores do tipo variável pode alterar e por isso eles são aplicados em circuitos que requerem sintonização, como os circuitos de rádio.
Atenção
Não se indica utilizar o capacitor variável em elevadas potências.
Atualmente o capacitor a óleo não é mais fabricado, sua aplicação era voltada para equipamentos de válvula que requerem elevada isolação. A construção deste capacitor se dava por meio de fitas de alumínio que eram enroladas em um papel embebido por óleo. De forma semelhante, o capacitor composto de papel não é mais produzido, sua construção era feita por meio de folhas metálicas e um tubo de papel embebido em cera. Os dois foram amplamente utilizados em eletrônica no passado, nos primórdios da eletrônica.
Quiz
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
MÓDULO 3
Identificar as formas de onda dos elementos passivos
A FORMA DE ONDA DOS ELEMENTOS PASSIVOS
Análise dos elementos passivos em regime permanente
A análise dos circuitos permite diversas observações em relação à sua alimentação, tal como o comportamento da fonte conectada (contínua ou alternada), se há fonte ou se este está desconectado, entre outras.
Comentário
É interessante avaliar os circuitos cuja operação se dá por meio de excitação contínua, ou seja, pela conexão de fontes cc.
Um circuito composto de elementos passivos, cuja alimentação é contínua, possui a característica de apresentar os valores de corrente e tensão estáveis após transcorrido o tempo. Após a estabilização do circuito, ou seja, ao atingir os valores constantes, é dito que ele opera em regime permanente. O tempo necessário para que esse regime seja alcançado é dado em segundos.
Capacitor como circuito aberto
Em regime permanente, o capacitor comporta-se como um circuito aberto (Módulo 2). Isso ocorre porque a tensão se estabiliza e, não havendo variação de tensão no tempo, a corrente é nula.
Indutor como curto-circuito
Em regime permanente (Módulo 1), o indutor comporta-se como um curto-circuito. A análise é feita como no capacitor e, não havendo variação da corrente no tempo, a tensão sobre esse elemento é nula.
Dadas essas duas considerações, nota-se que uma análise em regime permanente se trata de avaliar um circuito resistivo, caso este possua resistores.
Princípio da dualidade
Os indutores e capacitores são considerados elementos duais. Dois circuitos podem ser considerados duais, se as equações de malha de um deles possuem a mesma forma matemática que modela a equação nodal do outro.
Exemplo
São exemplos de grandezas duais:
- Resistência e condutância, uma vez que a condutância é o inverso da resistência.
- Tensão e corrente.
- Indutores e capacitores.
Em um indutor, há um fluxo magnético percorrendo o componente, enquanto no capacitor há cargas polarizando as placas condutivas. Para verificar a dualidade, consideram-se as equações de tensão e corrente dos dois componentes, já apresentadas nos Módulos anteriores:
$$v=L\frac{di}{dt}$$
$$i=C\frac{dv}{dt}$$
É notável que, ao alterar em uma das equações as variáveis i por v, bem como L por C (ou o oposto), as equações passam a ser equivalentes. A tabela a seguir representa valores duais para diversas grandezas elétricas:
| Valores Duais | |
|---|---|
| Tensão | Corrente |
| Carga | Fluxo |
| Resistência | Condutância |
| Indutância | Capacitância |
| curto-circuito | Circuito aberto |
| Impendância | Admitância |
| LKT | LKC |
Forma de onda
Em um circuito onde há somente resistores conectados, ao alterar o estado de uma chave, por exemplo, observa-se apenas a variação entre a presença das variáveis elétricas ou não, provocada pela descontinuidade. Nos casos em que se observa a presença de elementos passivos, essa análise se distingue.
Exemplo
Ao conectar uma fonte em um capacitor passa a existir o carregamento do componente, que ocorre em razão da polarização das placas. Esse valor aumenta gradativamente até atingir o regime permanente.
O período de variação em que o elemento sai do estado inicial até atingir o estado permanente é chamado de transitório.
Destacam-se os seguintes pontos:
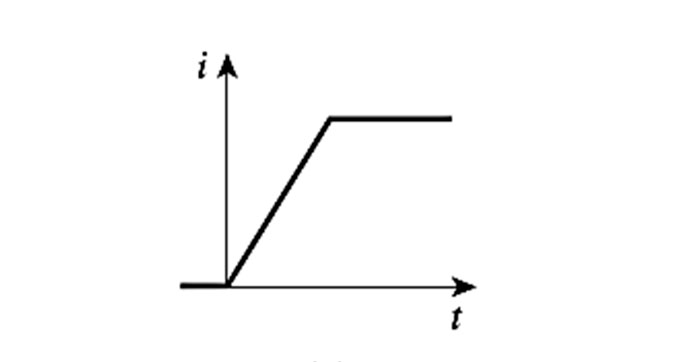
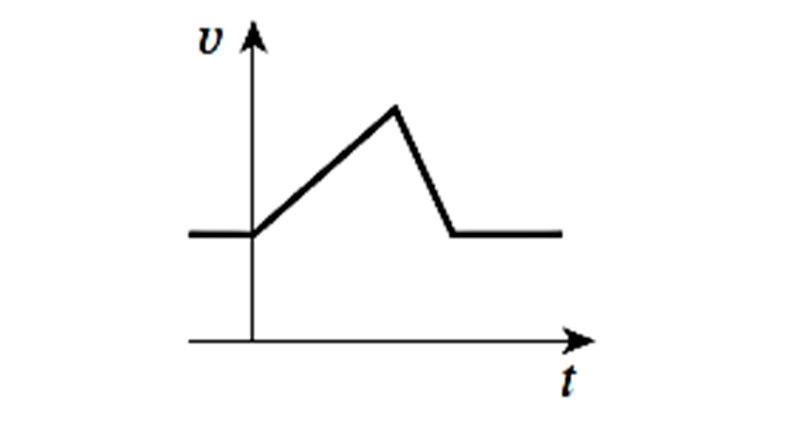
- A corrente em um indutor não pode mudar de forma instantânea, como se observa na representação abaixo:
- Observa-se uma mudança suave no valor da corrente, representada pela inclinação do gráfico.
- Conforme ocorre com a corrente em um indutor, a tensão em um capacitor não pode ser alterada de forma abrupta. Assim, observa-se o seguinte comportamento para a tensão:
Tensão e corrente
Representa a relação entre a tensão e a corrente.
Tensão no capacitor
Representa a tensão no capacitor.
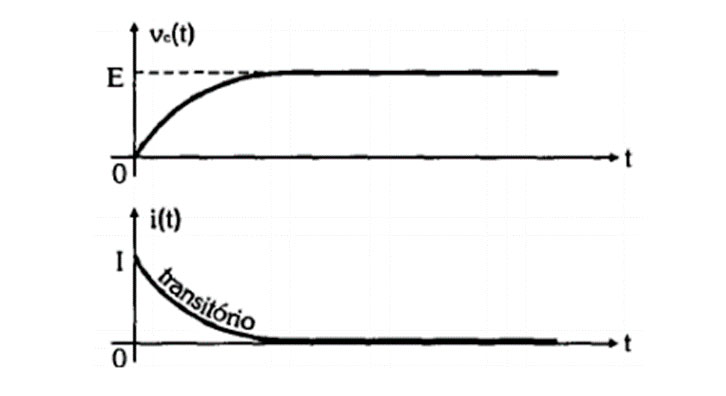
Considerando a análise de um circuito capacitivo, em que se avalia o momento de carga até o regime permanente, sabe-se que no instante inicial a corrente é máxima, enquanto a tensão é nula, o que pode ser observado nas seguintes curvas:
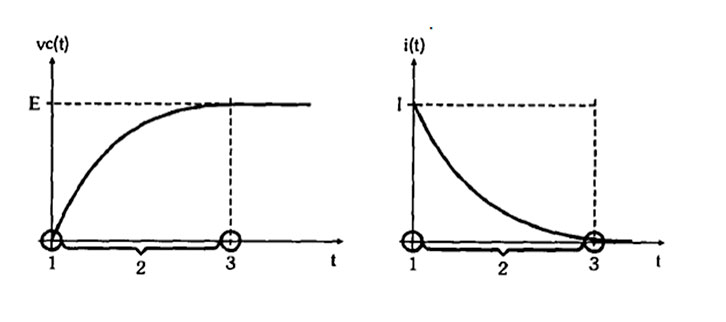
O capacitor sai do estado inicial e é carregado até alcançar o regime permanente. Em seguida, é possível observar o processo de descarga. A imagem abaixo representa o processo de transitório do capacitor para as grandezas de corrente e tensão, em que, a partir do ponto 3, este se encontra em regime permanente.
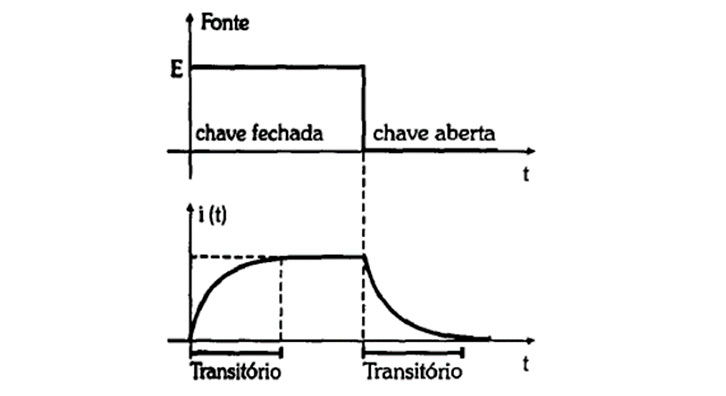
Para um indutor, o comportamento é um pouco distinto, podendo ser feitas algumas analogias. Observa-se que neste há existência de corrente, mesmo após o desligamento da fonte que o excita, o que faz desta uma característica do componente. O comportamento da corrente no indutor é similar à tensão do capacitor. À medida que o tempo passa, a corrente começa a decair.
Energia armazenada nos componentes passivos
Como sabemos, tanto o indutor quanto o capacitor são elementos caracterizados por armazenarem energia nos campos elétrico e magnético.
Saiba mais
A energia se refere ao trabalho necessário para que haja carregamento desses elementos.
Para um capacitor, a energia é armazenada no campo elétrico, dada a diferença de potencial aplicada aos terminais. Considerando as seguintes equações, que podem ser consultadas também no capítulo referente aos capacitores, a energia é calculada da seguinte forma:
$$w=C\frac{1}{2}v^2$$
Substituindo o valor da capacitância pelo valor definido: $$C=\frac{q}{v}$$, tem-se:
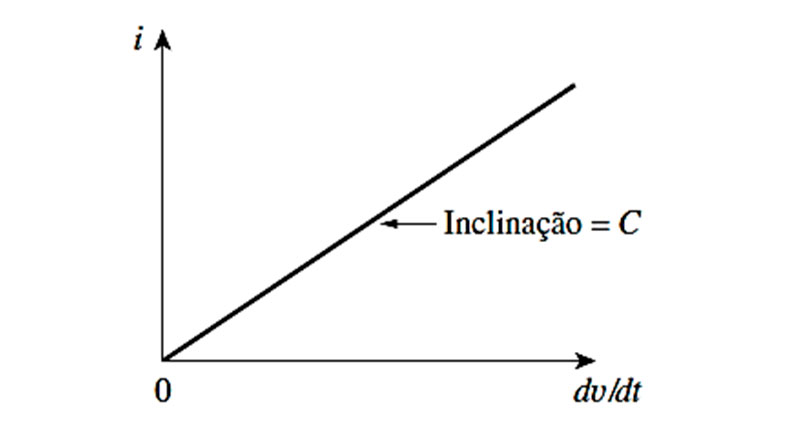
$$w=\frac{1}{2}qv$$
Na qual observa-se uma equação de comportamento linear. Assim, a energia pode ser descrita graficamente pela imagem abaixo:
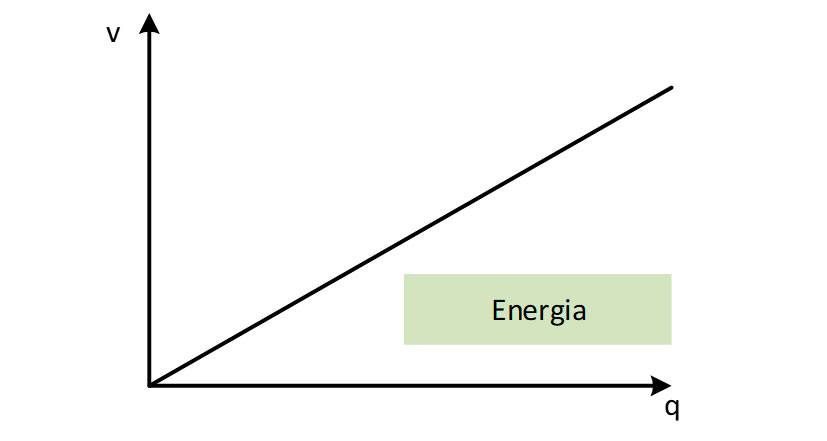
Atenção
A mesma análise pode ser feita para um indutor.
Um indutor é capaz de armazenar energia no campo magnético. Esse armazenamento se dá quando o componente é percorrido por uma corrente elétrica (a equação que descreve esse armazenamento foi citada no Módulo 1), dada por:
$$w=L\frac{1}{2}i^2$$
Essa energia é conservativa.
Circuitos singulares
Por definição, as funções singulares são aquelas que apresentam alguma descontinuidade ou que têm derivadas descontínuas. A função de singularidade serve para representar o comportamento comutativo do circuito. Sendo assim, em situações em que são observados componentes como chaves, existe uma descontinuidade, sendo então possível representar as formas de onda de corrente e tensão através da utilização das funções singulares.
Das funções mais utilizadas, podem ser citadas:
A figura mostra uma particularidade desta função, conhecida por degrau unitário. Em zero, esta função apresenta descontinuidade; em 1, muda de estado de forma abrupta. Assim, a aplicação dela pode ocorrer quando se deseja representar alterações de tensão ou corrente de modo instantâneo: em dado instante o circuito está desligado e, em seguida, passa a existir uma excitação, isto equivale a uma comutação de chaves.
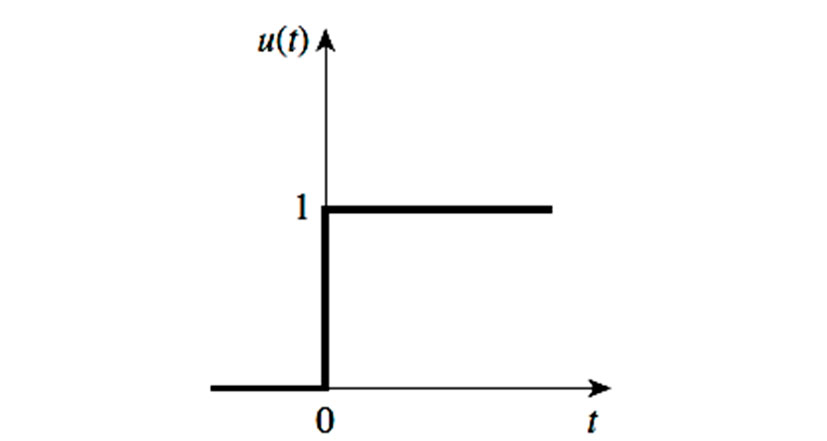
Atenção
A derivada da função degrau resulta na função impulso.
Pode também ser identificada por função delta, sendo a derivada da função degrau. Como no caso anterior, a função impulso unitário é um caso particular da função impulso, onde a amplitude atingida é 1. É importante destacar que esta é fisicamente impraticável, porém, para fins de estudo, pode representar situações como choques elétricos.
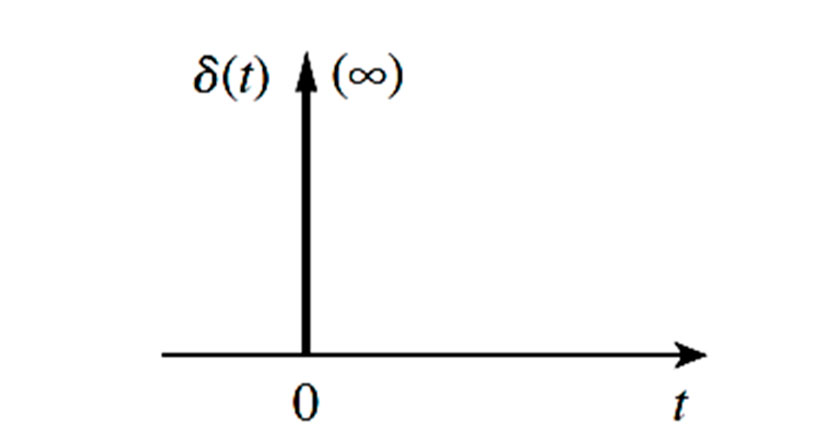
Pode ser obtida pela integração da função degrau. A imagem abaixo apresenta um caso particular: a função rampa unitária.
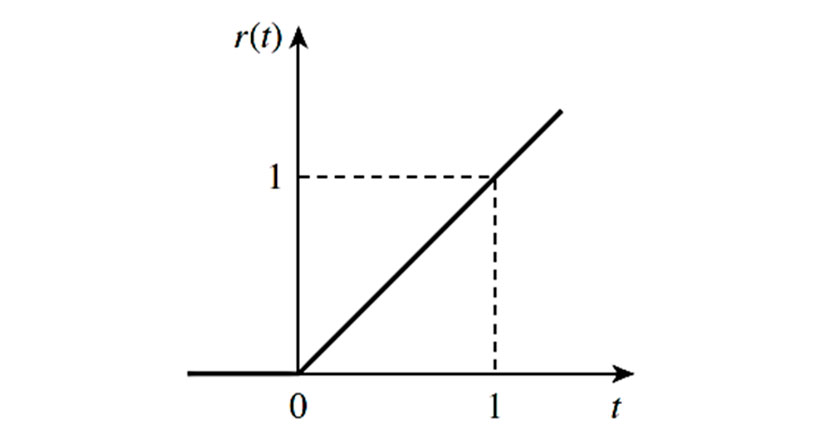
Atenção
Podemos combinar as funções de maneira a analisar de forma única cada componente do circuito elétrico.
Verificando o aprendizado
ATENÇÃO!
Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:
O conteúdo ainda não acabou.
Clique aqui e retorne para saber como desbloquear.
Conclusão
Considerações Finais
O estudo deste material teve por objetivo a apresentação dos elementos armazenadores de energia, suas características básicas e a forma como são utilizados nos circuitos elétricos. Assim, mostramos exemplos de cálculos e o uso de técnicas de solução e simplificação.
No módulo 1, foram pontuados os aspectos básicos do indutor, a forma de associá-lo, o cálculo de potência e energia. Na sequência, o módulo 2 tratou dos mesmos aspectos, no entanto, com foco no capacitor. Por fim, no módulo 3, foram esclarecidas as dualidades entre os dois componentes, as funções usadas para o seu estudo, todos acompanhados de exemplos de cálculos.
Podcast
CONQUISTAS
Você atingiu os seguintes objetivos:
Descreveu o elemento indutor
Empregou o elemento capacitor
Identificou as formas de onda dos elementos passivos