Descrição

Classificações, cálculo de escoamento em regime permanente e uniforme, energia específica, transições de seção, ressalto hidráulico, noções de cálculo em escoamento variado e seções compostas.

PROPÓSITO

Compreender o comportamento dos escoamentos em condutos livres e os procedimentos básicos para cálculo e dimensionamento.

Preparação

Antes de iniciar este conteúdo, certifique-se de que tem acesso à calculadora do seu dispositivo e tenha em mãos papel e caneta para possibilitar a resolução dos exercícios. Para solução de alguns problemas, é necessário ter acesso a um aplicativo de planilha eletrônica (ex.: Google Planilhas, Excel e OpenOffice Calc).

OBJETIVOS

Módulo 1

Calcular os parâmetros de escoamento em regime permanente e uniforme

Módulo 2

Analisar o escoamento em condutos livres por meio da energia específica

Módulo 3

Identificar o perfil do nível d’água em escoamentos variados

Módulo 4

Reconhecer a performance de seções compostas

Escoamento em condutos livres

MÓDULO 1

Calcular os parâmetros de escoamento em regime permanente e uniforme

Introdução

Cálculo em regime permanente e uniforme

Escoamentos em condutos livres, comumente chamados de canais, são objetos de estudo em diversas áreas, como saneamento, drenagem, irrigação e navegação.

Para dimensionar corretamente esses condutos, é necessário um conjunto de conhecimentos baseados na mecânica dos fluidos, que serão relembrados e aplicados aqui.

Classificações de canais livres

Existem dois tipos de escoamento estudados na Hidráulica:

Imagem: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento.

Conduto forçado

O fluido é impulsionado pela diferença de pressão, portanto, ela será diferente da atmosférica e variará ao longo da tubulação, mas a gravidade também pode contribuir.

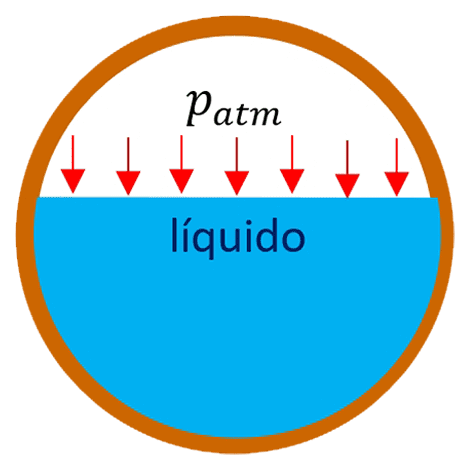
Conduto livre

O fluido é impulsionado apenas pela gravidade, e a pressão da sua superfície livre é constante e igual à atmosférica.

Neste conteúdo, apresentaremos apenas a análise de condutos livres, que incluem rios, canais, galerias, bueiros, valetas e sarjetas. Esses condutos são aplicados em drenagem, irrigação, saneamento e navegação.

Para simplificar, os condutos livres, de maneira geral, serão chamados de canais.

Os canais podem ser classificados em:

Naturais

São os cursos d’água moldados pela natureza (ex.: rios e córregos).

Artificiais

Construídos pelo homem, de seção aberta ou fechada (ex.: canais de irrigação, de navegação, galerias e bueiros).

Saiba mais

Os canais naturais tendem a possuir meandros, que são mudanças bruscas de direção, como vimos em foto. No passado, com intuito de reverter as enchentes causadas pela ocupação das margens de rios, retificava-se os canais naturais, causando aumento de velocidade e, consequentemente, diminuição da altura d’água em determinadas seções.

Com o tempo, percebeu-se que essa prática intensificava enchentes em seções mais abaixo (a jusante), transferindo o “problema” para bairros ou municípios vizinhos.

Por isso, muitos países estão, atualmente, revertendo isso, naturalizando canais que foram retificados e adotando outras medidas para evitar as enchentes.

Quanto à geometria da seção, os canais podem ser:

Prismáticos

Possuem seção transversal e declividade de fundo constantes ao longo do comprimento.

Não prismáticos

Têm variações de seção, declividade do fundo ou revestimento.

Usualmente, para possibilitar a modelagem com base nos métodos básicos, os canais não prismáticos são divididos em seções que podem ser simplificadas como trechos prismáticos. Portanto, estudaremos apenas esse tipo. O escoamento em canais pode ser classificado, em relação ao regime temporal, em permanente ou transiente e, em relação à declividade do nível d’água (N.A.), em uniforme ou variado − esse último sendo subdividido entre gradualmente e bruscamente variado.

Classificação de escoamentos em canais.

A imagem a seguir exemplifica a ocorrência de todas as possibilidades para um escoamento permanente ao longo de um mesmo canal. Após um comprimento suficientemente longo, o escoamento atinge o equilíbrio, permanecendo então o nível d’água (N.A.) constante, em relação ao fundo (paralelo).

Escoamento permanente uniforme, gradualmente e bruscamente variado.

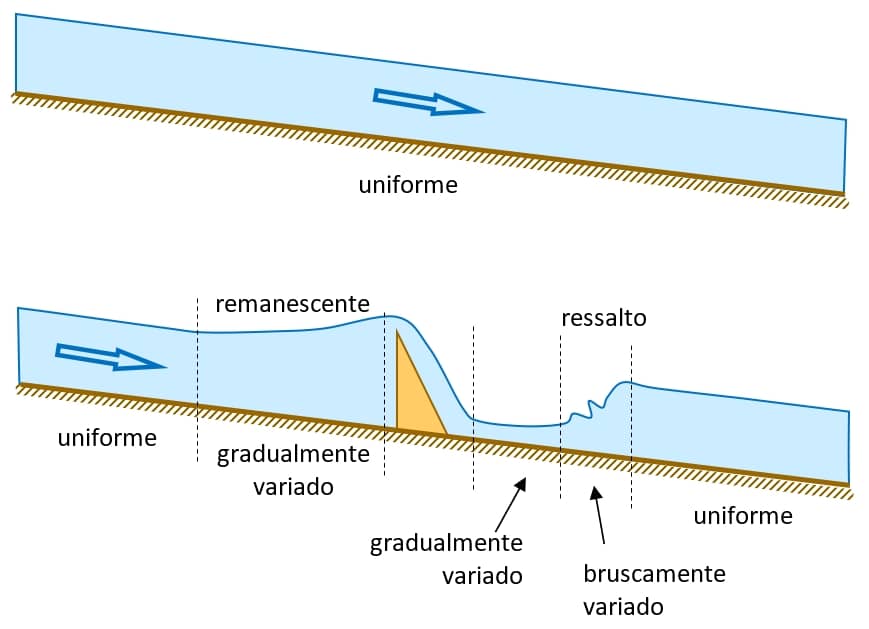
Um obstáculo tende a causar a elevação do N.A., o que se propaga para montante em um efeito denominado remanso. A descida acentuada do obstáculo (ex.: vertedor − estrutura hidráulica utilizada para medição de vazão) força uma velocidade muito elevada, sendo reestabelecida para aquela correspondente ao equilíbrio após uma variação brusca, que é chamada de ressalto hidráulico.

Principais parâmetros

Geral

Os parâmetros mais relevantes para o estudo do escoamento em canais são indicados na imagem a seguir:

Parâmetros em canais.

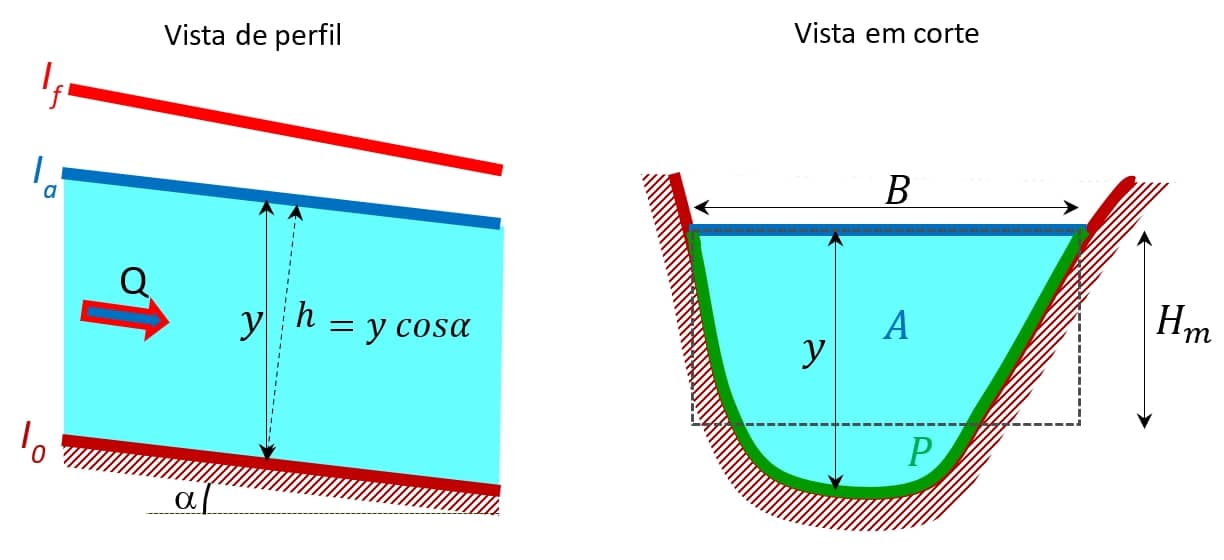
O significado de cada um desses parâmetros é detalhado no quadro a seguir:

Símbolo	Nome	Descrição
$$A$$	Área molhada	Área da seção transversal efetivamente ocupada por água
$$P$$	Perímetro molhado	Comprimento ao longo da seção transversal onde há contato entre água e revestimento do canal
$$R_h$$	Raio hidráulico	Razão entre $$A$$ e $$P,$$ $$R_h=A/P$$
$$y$$	Altura ou tirante d’água	Altura da linha d’água a partir do fundo, medida na vertical
$$h$$	Altura de escoamento	Altura da linha d’água, medida na direção perpendicular ao fundo
$$B$$	Largura de topo	Distância entre margens na altura do N.A.
$$H_m$$	Altura hidráulica ou média	Razão entre $$A$$ e $$B,$$ $$H_m=A/B.$$ Equivale à altura que, multiplicada por $$B$$, resulta em $$A$$
$$I_o$$	Declividade de fundo	Razão entre redução da cota de fundo $$\Delta z$$ e distância horizontal $$\Delta x$$ percorrida. Por possuir valores pequenos, normalmente é medida em metro por quilômetro (m/km)
$$I_a$$	Declividade da linha d’água	Análogo à $$I_o,$$ porém, referente à linha d’água
$$I_f$$	Declividade da linha de energia	Razão entre decréscimo da carga (energia) do escoamento $$\Delta H$$ e a distância horizontal percorrida $$\Delta x$$

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 1: Parâmetros geométricos em canais.
Elaborado por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento

A partir desses parâmetros, podemos calcular o número de Reynolds por:

$R e = \frac{ρ V D_{h}}{μ}$

$D_{h} = 4 R_{h}$

Equação 1

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$\rho$$ é a massa específica ($$\rho = 998 kg/m³,$$ para água à 20°C), $$V$$ é a velocidade média do escoamento na seção (em m/s), $$\mu$$ é a viscosidade ($$\mu = 0,001kg/m.s,$$ para água à 20°C) e $$D_h$$ é o diâmetro hidráulico, calculado por $$D_h=4R_h.$$ Se $$Re < 2000,$$ o escoamento é classificado como laminar e, se $$Re > 8000,$$ como turbulento. Entre esses valores ocorre uma transição.

Se você calcular o $$Re$$ para qualquer combinação de valores típicos de escoamento em canais, verá que será sempre turbulento. Sendo assim, o adimensional (sem unidade de medida) mais relevante para escoamento em canais passa a ser o número de Froude, definido por:

$F r = \frac{V}{\sqrt{g H_{m}}}$

Equação 2

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Que classifica o escoamento em:

$F r < 1$ : subcrítico (fluvial).
$F r = 1$ : crítico.
$F r > 1$ : supercrítico (torrencial).

Seções trapezoidais

Uma seção transversal trapezoidal pode ser representada por três parâmetros geométricos: largura de fundo $$b,$$ altura $$y$$ (tirante) e declividade de talude, como podemos ver na imagem a seguir. Esse último, comumente, é medido pela razão entre comprimento e altura da rampa do talude, que aqui chamaremos de $$Z.$$

Imagem 7: Parâmetros geométricos da seção trapezoidal.

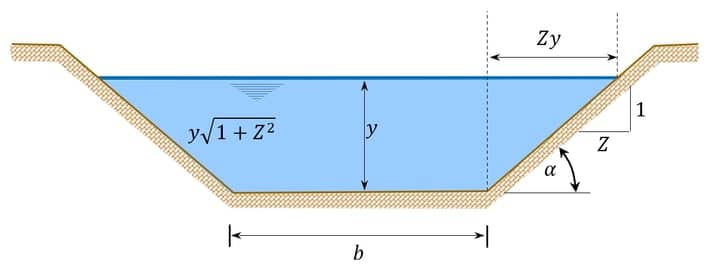
Sendo assim, a área $$A,$$ largura de topo $$B,$$ perímetro molhado $$P$$ e raio hidráulico $$R_h$$ serão obtidos por:

$A = (b + Z y) y$

$B = b + 2 Z y$

$P = b + 2 y \sqrt{1 + Z^{2}}$

$R_{h} = \frac{A}{P} = \frac{(b + Z y) y}{b + 2 y \sqrt{1 + Z^{2}}}$

Equação 3

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Observe que esses parâmetros também podem representar seção triangular $$(b=0)$$ e retangular $$(Z=0).$$

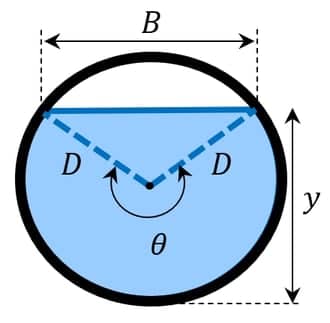
Seções circulares

As seções circulares, por sua vez, podem ser definidas apenas com o diâmetro $$D$$ e a altura.

Para simplificar, vamos fazer o equacionamento com base no ângulo interno $$\theta.$$ Sendo assim:

$A = D^{2} \frac{(θ - s e n θ)}{8}$

$B = D s e n (\frac{θ}{2})$

$P = \frac{θ D}{2}$

$R_{h} = \frac{A}{P} = D \frac{(θ - s e n θ)}{4 θ}$

$θ = 2 \arccos (1 - 2 \frac{y}{D})$

Equação 4

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Vamos ver um exemplo.

Exemplo 1

Em um canal regular de seção trapezoidal de declividade constante, com largura de fundo igual a 1,50m, inclinação dos taludes 2H:1V, a altura d’água é igual a 0,65m e a velocidade média, 0,70m/s. Classifique o escoamento com base nos números de Reynolds e Froude.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Os parâmetros da seção transversal serão:

$b = 1, 5 m$ ; $Z = 2$ (razão entre o comprimento e altura do talude) e $y = 0, 65 m$

Com base nas equações em 3:

$A = (b + Z y) y = (1, 5 + 2 \cdot 0, 65) \cdot 0, 65 = 1, 82 m^{2}$

$B = b + 2 Z y = 1, 5 + 2 \cdot 2 \cdot 0, 65 = 4, 10 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

$P = b + 2 y \sqrt{1 + Z^{2}} = 1, 5 + 2 \cdot 0, 65 \cdot \sqrt{1 + 2^{2}} = 4, 4 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Então:

$R_{h} = \frac{A}{P} = \frac{1, 85}{4, 41} = 0, 42 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela equação 1:

$D_{h} = 4 R_{h} = 4 \cdot 0, 42 = 1, 68 m$

$R e = \frac{ρ V D_{h}}{μ} = \frac{998 \cdot 0, 70 \cdot 1, 68}{10^{- 3}} = 1, 2 \cdot 10^{6}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A altura hidráulica, conforme o Quadro 1 é definida por:

$H_{m} = \frac{A}{B} = \frac{1, 82}{4, 1} = 0, 44 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

E pela equação 2:

$F r = \frac{V}{\sqrt{g H_{m}}} = \frac{0, 7}{\sqrt{9, 8 \cdot 0, 44}} = 0, 34$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Portanto:

Como $$Re>8000,$$ o escoamento é turbulento.

Como $F r < 1$ , o escoamento é subcrítico (ou fluvial).

Cálculo do escoamento permanente e uniforme

Equação da tensão cisalhante

Neste tópico, vamos equacionar o escoamento quando ele é permanente e uniforme, o que classifica a maior parte dos cálculos feitos em projetos de canais. Assumiremos uma distribuição hidrostática de pressão ao longo da profundidade, o que tem boa precisão se a declividade do fundo não tiver uma variação acentuada.

Há também uma variação da velocidade ao longo da seção transversal, que vai de zero junto à parede até um valor máximo, que estará um pouco abaixo da superfície. O valor não será máximo na superfície devido ao cisalhamento na interface ar-água.

Na imagem a seguir, é representado um trecho de canal com escoamento permanente e uniforme:

Imagem 9: Forças atuando no escoamento permanente e uniforme de canais.

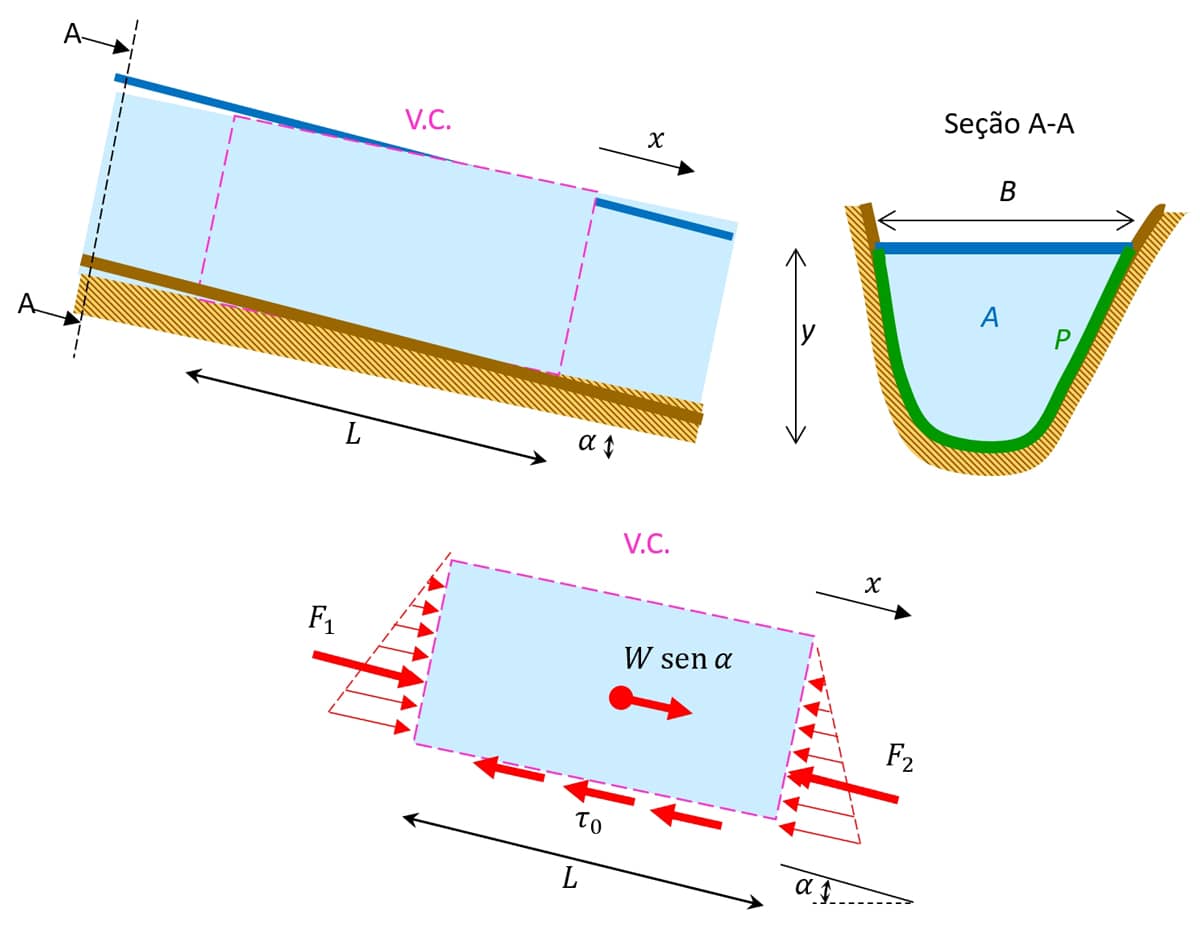
Analisaremos as forças que atuam em um volume de controle (V.C.) com comprimento L, sendo elas:

Projeção do peso $$W$$ na direção do escoamento $$(x),$$ calculado pelo peso específico $$\gamma$$ multiplicado pelo volume $V$ do $$V.C.,$$ onde $$\gamma$$ é o produto da massa específica pela gravidade $$(\gamma=\rho g).$$

Resultantes $$F_1$$ e $$F_2$$ da pressão distribuída nas aberturas de entrada e saída do $$V.C.,$$ respectivamente.

Força de resistência decorrente da tensão cisalhante $$\tau_0$$ (“atrito”) do líquido com o revestimento do canal.

Vamos desprezar a resistência causada pelo ar, na superfície.

O somatório das forças atuantes deve ser nulo, pois o escoamento é permanente:

$\sum F_{x} = F_{1} + \overset{γ \forall = γ A L}{\overset{⏞}{W}} \cdot s e n α - F_{2} - τ_{0} \cdot \overset{P L}{\overset{⏞}{A_{r}}} = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$A_r$$ é a área de contato entre o revestimento do canal e o líquido que escoa, e $V$ é o volume do $$V.C.$$ Em se tratando de escoamento uniforme (linha d’água paralela ao fundo), a altura d’água é constante, portanto, a força $$F_1$$ será igual à $$F_2,$$ considerando-se distribuição hidrostática de pressão $$(p=\rho gy).$$ Sendo assim:

$τ_{0} P L = γ A L sen α$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para pequenos ângulos de fundo − o que quase sempre ocorre para as aplicações que objetivamos −, o seno é, aproximadamente, igual à tangente que, por sua vez, é igual à declividade de fundo $$I_0$$ (Quadro 1) . Então, a expressão anterior se reduz a:

$τ_{0} = \frac{γ A I_{0}}{P} = \overset{ρ g}{\overset{⏞}{γ}} R_{h} I_{0}$

Equação 5

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$\tau_0$$ é em Pa, e $$I_0$$ em m/m.

Vamos ver um exemplo.

Exemplo 2

Qual é a tensão cisalhante na parede de um tubo de esgoto com 80cm de diâmetro e preenchido até meia seção em um trecho com declividade de 0,50m/km?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Conforme a equação (4), sendo para meia seção $$\theta=180°=π$$ (Figura 8):

$A = D^{2} \frac{(θ - sen θ)}{8} = {(0,80)}^{2} \cdot \frac{(π - sen π)}{8} = 0,25 m ²$

$P = \frac{θ D}{2} = \frac{π \cdot 0,80}{2} = 1,26 m$

$R_{h} = \frac{A}{P} = 0,20 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela equação (5), adotando a massa específica da água:

$τ_{0} = ρ g R_{h} I_{0} = 1000 \cdot 9,8 \cdot 0,2 \cdot \frac{0,5}{1000} ≅ 1,0 P a$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Esse é o valor mínimo de tensão cisalhante exigido pela norma NBR 9649 – Projeto de redes coletoras de esgoto sanitário. O objetivo dessa recomendação é forçar uma “autolimpeza” dos tubos, evitando a sedimentação nas paredes.

Equação de Manning

Um parâmetro bastante útil é a velocidade de atrito, definida como $$u^\ast=\sqrt{\tau_0/\rho}=V\sqrt{f/8}.$$ Substituindo-se essa relação da equação (5), obtemos

$V = \overset{C}{\overset{⏞}{\sqrt{\frac{8 g}{f}}}} \sqrt{R_{h} I_{0}}$

Equação 6

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Que é conhecida como equação de Chézy. Manning estabeleceu que $C = \frac{R_{h}^{1 / 6}}{n}$ originando a expressão:

$V = \frac{1}{n} R_{h}^{2 / 3} I_{0}^{1 / 2}$

$Q = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2}$

Equação 7

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Ambas são correspondentes ao Sistema Internacional de Unidades − S.I. (vazão em m³/s).

Conhecida como equação de Manning, onde $$n$$ é um coeficiente que está relacionado à rugosidade do revestimento do canal, como vemos no quadro 2.

Material	Condições
Material	Muito boa	Boa	Regular	Má
Tubos de concreto	0,012	0,013	0,015	0,016
Superfícies de argamassa de cimento	0,011	0,012	0,013	0,015
Superfícies de cimento alisado	0,010	0,011	0,012	0,013
Alvenaria de pedra argamassada	0,017	0,020	0,025	0,030
Calhas metálicas lisas (semicirculares)	0,011	0,012	0,013	0,015
Canais abertos em rocha (irregular)	0,035	0,040	0,045	-
Canais c/ fundo em terra e talude c/ pedras	0,028	0,030	0,033	0,035
Canais c/ leito pedregoso e talude vegetado	0,025	0,030	0,035	0,040
Canais com revestimento de concreto	0,012	0,014	0,016	0,018
Canais de terra (retilíneos e uniformes)	0,017	0,020	0,023	0,025
Gabião	0,022	0,030	0,035	-
Tubos de ferro galvanizado	0,013	0,014	0,015	0,017
Córregos e rios limpos, retilíneos e uniformes	0,025	0,028	0,030	0,033
Igual à anterior, porém c/ pedras e vegetação	0,030	0,033	0,035	0,040
Igual à anterior, com meandros, bancos e poços, limpos	0,035	0,040	0,045	0,050
Margens espraiadas, pouca vegetação	0,050	0,060	0,070	0,080
Margens espraiadas, muita vegetação	0,075	0,100	0,125	0,150

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 2: Valores de coeficiente de Manning.
Extraído de Porto (2004).

Determinar esses valores pode ser uma tarefa trabalhosa, pois o projetista deve comparar o tipo de revestimento com os disponíveis na literatura, levando em consideração as condições. Além disso, observa-se, pela equação de Manning, que o $$n$$ tem um impacto expressivo no cálculo, o que torna ainda mais crítica a escolha do valor a ser adotado.

Vejamos um exemplo.

Exemplo 3

Para o exemplo anterior, considerando que os tubos são de concreto em boas condições, calcule a vazão escoada.

Dados do problema anterior: tubo de esgoto com 80cm de diâmetro e preenchido até meia seção em um trecho com declividade de 0,50m/km.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Já calculamos, no exemplo anterior, que $A = 0,25 m ²$ e $R_{h} = 0,20 m$ .

Para tubo de concreto em boas condições, $$n = 0,013$$, conforme quadro 2. Segundo a equação de Manning 7:

$Q = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2} = \frac{0,25}{0,013} {(0,2)}^{2 / 3} {(\frac{0,5}{1000})}^{1 / 2} = 0,15 m^{3} / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Quando conhecemos a altura d’água (tirante) e desejamos calcular a vazão, a solução da equação 7 de Manning é simples e direta, pois podemos calcular o raio hidráulico e a área.

Quando o problema é o contrário, ou seja, conhecemos a vazão e desejamos saber a altura, o resultado não é facilmente obtido pela equação 7. Uma alternativa é implementar essa equação em uma calculadora científica ou planilha eletrônica e testar diversos valores de $$y$$ até que o $$Q$$ calculado seja o desejado, o que constitui um método de tentativa e erro.

Saiba mais

Uma alternativa de cálculo automatizado da profundidade é através de recursos de otimização disponíveis em planilhas eletrônicas como “Solver” e “Atingir meta” do Excel. Com eles, é possível fazer com que o computador procure o valor da variável de entrada $$y,$$ para que a vazão calculada seja igual a um determinado valor. Experimente fazer os próximos exemplos com esses recursos.

Veremos, a seguir, um método que possibilita o cálculo manual da altura a partir de uma determinada vazão.

Cálculo da altura

Em um projeto de canais, normalmente, os dados de partida para o dimensionamento dos condutos são:

Clique nas barras para ver as informações. Objeto com interação.

Vazão

Resultado de uma análise hidrológica, ou seja, previsão de intensidade de chuva, normalmente feita com base em estudo estatístico da série histórica em uma determinada região. Trata-se de um dado crítico, pois nem sempre se possui medições de precipitação de longo período, necessárias para uma boa previsão, que também pode ser subdimensionada devido às mudanças climáticas.

Declividade de fundo

Será função das diferenças de cotas possibilitadas pela topografia.

Tipo de revestimento

Deve ser determinado em fases iniciais do projeto, com base no tipo de empreendimento e na experiência com outros casos semelhantes.

Sendo assim, resta calcular qual será a altura d’água para uma determinada seção. Portanto, é conveniente adequarmos a equação 7 de Manning, deixando de um lado os dados de entrada e, do outro, o que deverá ser calculado:

$\frac{n Q}{\sqrt{I_{0}}} = A R_{h}^{2 / 3}$

Equação 8

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Seção retangular muito larga (b >> y)

Em uma seção retangular, a área, o perímetro molhado e o raio hidráulico são calculados por:

$A = b y$

$P = b + 2 y$

$R_{h} = \frac{A}{P} = \frac{b y}{b + 2 y}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Se o canal for muito largo, o que significa $$b\gg y,$$ o $$y$$ no denominador da fórmula de $$R_h$$ passa a ser desprezível, quando somado à $$b,$$ e, portanto:

$R_{h} ≅ \frac{b y}{b} = y$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Substituindo-se essa relação na equação de Manning 8:

$\frac{n Q}{\sqrt{I_{0}}} = (b y) y^{2 / 3}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

E isolando a altura:

$y = {(\frac{n Q}{b \sqrt{I_{0}}})}^{3 / 5}$

Equação 9

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Essa é a única condição em que é possível calcular, analiticamente, a altura d’água com cálculo exato e direto.

Seção trapezoidal (incluindo retangular e triangular)

Substituindo o raio hidráulico e a declividade de fundo conforme a equação 3, a equação anterior pode ser rearranjada como:

$K_{T y} = \frac{n Q}{b^{8 / 3} \sqrt{I_{o}}} = {(\frac{y}{b})}^{5 / 3} \frac{{[1 + (\frac{y}{b}) Z]}^{5 / 3}}{{[1 + 2 (\frac{y}{b}) \sqrt{1 + Z ²}]}^{2 / 3}}$

Equação 10

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$K_{Ty}$$ é um adimensional definido para facilitar a obtenção da altura $$y$$ em canais trapezoidais. Variando-se os valores de $$y/b$$ e $$Z,$$ é possível montar uma tabela ou gráfico que forneça, para um determinado valor de $$K_{Ty}$$ e $$Z,$$ o valor de $$y.$$

Vamos ver um exemplo.

Exemplo 4

Calcule o tirante de um canal de seção retangular com largura de 1,5m aberto em rocha em condições regulares, declividade de fundo de 0,4m/km e vazão de 0,30m³/s.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Para canal retangular, $$Z=0$$ (imagem 7). Nesse problema, $$n=0,045$$ (quadro 2).

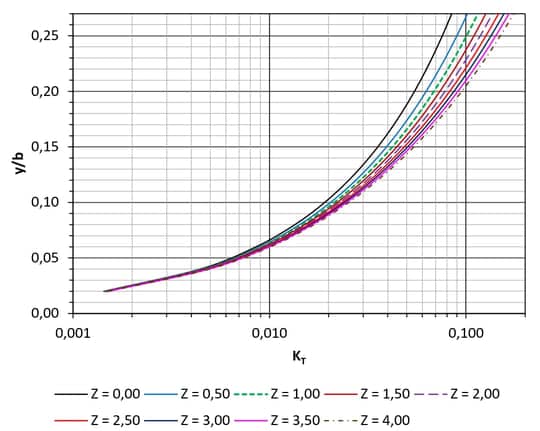
Conforme a equação 10:

$K_{T y} = \frac{n Q}{b^{8 / 3} \sqrt{I_{o}}} = \frac{0,045 \cdot 0,3}{{(1,5)}^{8 / 3} \sqrt{\frac{0,4}{1000}}} = 0,23$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Buscando esse valor no eixo das abscissas no gráfico da Figura 11 e cruzando com a primeira curva $$(Z=0),$$ obtemos:

$\frac{y}{b} = 0,56 \to y = 1,5 \cdot 0,56 = 0,84 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Observa-se que não se espera uma precisão muito elevada nesse cálculo, tendo em vista todas as variantes do problema.

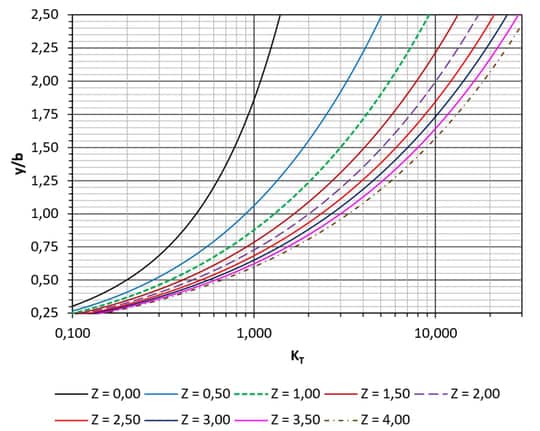
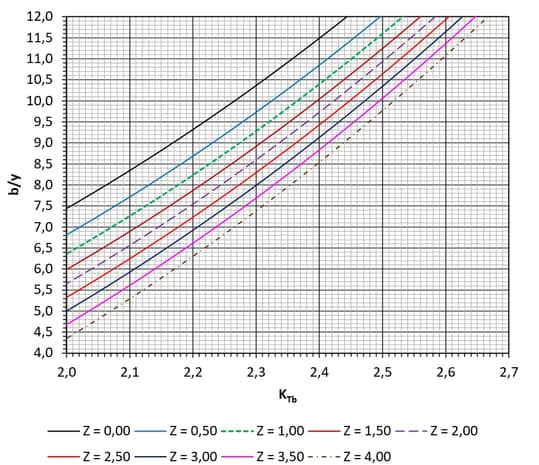
Caso o dado de entrada seja $$y$$ e quisermos calcular $$b,$$ a equação (10) pode ser reescrita obtendo-se:

$K_{T b} = {(\frac{n Q}{\sqrt{I_{o}}})}^{3 / 8} = y_{0} {[\frac{{(m + Z)}^{5}}{{(m + 2 \sqrt{1 + Z ²})}^{2}}]}^{1 / 8}$

Equação 11

Atenção! Para visualização completa da equação utilize a rolagem horizontal

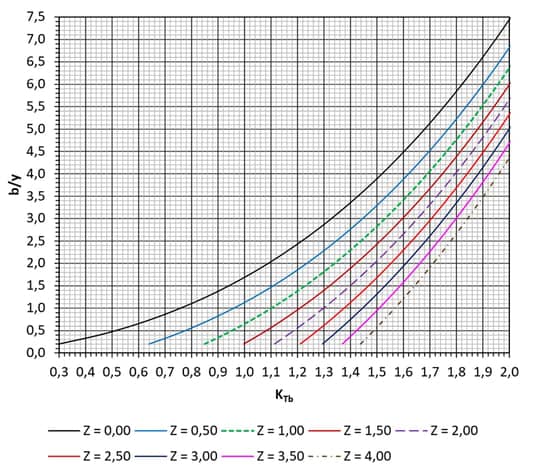
Onde $$K_{Tb}$$ é um adimensional definido para facilitar a obtenção da base $$b$$ em canais trapezoidais através da imagem 12 e da imagem 13.

Um exemplo de adoção desse caminho de cálculo é quando há uma restrição para escavação, limitando a profundidade do canal, ou seja, a altura d’água. Então, esse valor máximo passa a ser um dado de entrada, e nos resta saber qual será a largura necessária.

Canais circulares

Para seção circular, substituiremos as equações de 4 na de Manning 8:

$K_{C} = \frac{1}{D} {(\frac{n Q}{\sqrt{I_{0}}})}^{3 / 8} = {[\frac{{(θ - s e n θ)}^{5}}{2^{13} θ^{2}}]}^{1 / 8}$

$\frac{y_{0}}{D} = \frac{1}{2} (1 - \cos \frac{θ}{2})$

Equação 12

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Variando-se o valor de $$\theta$$ entre 0° e 360°, é possível montar uma tabela ou gráfico como na imagem 14, que relaciona $$y/D$$ com o adimensional $$K_C.$$

Imagem 14: Cálculo da altura d’água para canais circulares.

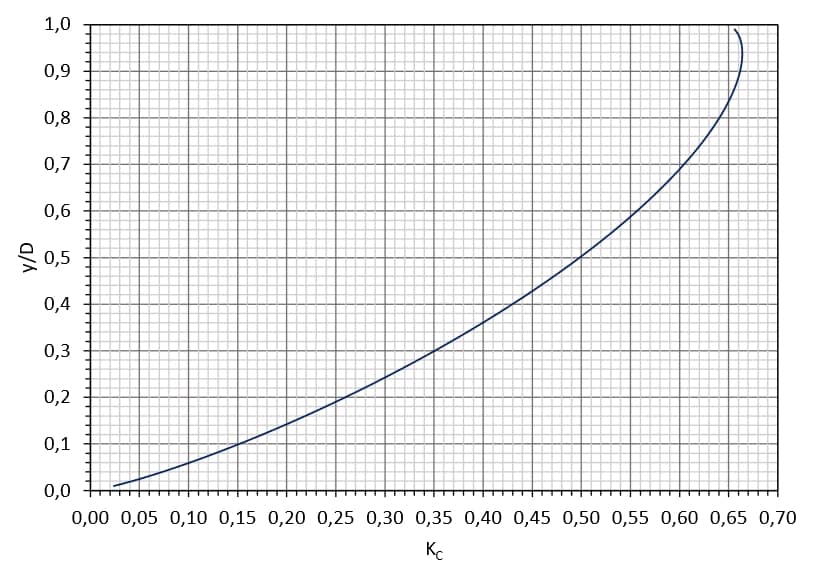
Nesse gráfico, observamos que há um valor máximo de vazão e que ele ocorre para $$y/D=0,94,$$ ou seja, quando a altura da seção circular está 94% preenchida. Nessa situação, $$K_C=0,664.$$

Vamos ver um exemplo.

Exemplo 5

Determine o tirante em uma galeria de águas pluviais de concreto com $$n = 0,013,$$ diâmetro de 1,0m e declividade de fundo de 3m/km, transportando uma vazão de 850L/s em regime permanente e uniforme.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Pela equação 12:

$K_{C} = \frac{1}{D} {(\frac{n Q}{\sqrt{I_{0}}})}^{3 / 8} = \frac{1}{1,0} \cdot {(\frac{0,013 \cdot 0,85}{\sqrt{0,003}})}^{\frac{3}{8}} = 0,55$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Consultando no gráfico da imagem 14, obtemos:

$\frac{y}{D} = 0,59 \to y = 1,0 \cdot 0,59 = 0,59 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Eficiência hidráulica de seções

Analisando-se a equação de Manning 8, constatamos que, para uma determinada área $$A,$$ a vazão $$Q$$ será máxima quando o perímetro molhado $$P$$ for mínimo, pois está no denominador do raio hidráulico $$R_h=A/P.$$ Essa seria uma condição de máxima eficiência hidráulica. Além disso, o perímetro molhado está diretamente associado ao custo da obra, pois o revestimento assume uma parcela significativa. Portanto, o mínimo perímetro molhado é uma condição desejável para otimização do dimensionamento do projeto. Para calculá-lo em uma seção trapezoidal, vamos reescrever as equações em 3, substituindo:

$m = \frac{b}{y}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$m$$ é chamado de razão de aspecto.

$A = (m + Z) y^{2} \to y = \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}}$

$P = (m + 2 \sqrt{1 + Z^{2}}) y$

$\begin{matrix} A = (m + Z) y^{2} \to y = \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}} \\ P = (m + 2 \sqrt{1 + Z^{2}}) y \end{matrix}\} \to P = (m + 2 \sqrt{1 + Z^{2}}) \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para encontrar o valor de $$m$$ para o qual $$P$$ é mínimo, faremos:

$\frac{d P}{d m} = 0$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Que fornece:

$m = \frac{b}{y} = 2 (\sqrt{1 + Z ²} - Z)$

Equação 13

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A combinação entre as equações em 3 e a equação de Manning 8 pode ser refeita, explicitando-se $$m:$$

$M = {(\frac{n Q}{\sqrt{I_{0}}})}^{3 / 8}$

$K_{m} = {[\frac{{(m + Z)}^{5}}{{(m + 2 \sqrt{1 + Z^{2}})}^{2}}]}^{1 / 8}$

$y = \frac{M}{K_{m}}$

Equação 14

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$M$$ é chamado de coeficiente dinâmico, medido em metros, e $$K_m$$ é o fator de forma (adimensional).

Portanto, se desejamos calcular uma seção com máxima eficiência hidráulica, o valor da razão de aspecto m deve ser obtida por 13, depois a altura de escoamento $$y$$ é calculada por 14. Por fim, a base é dimensionada a partir da definição da razão de aspecto, $$b=ym.$$

Vamos ver um exemplo.

Exemplo 6

Qual deve ser a razão de aspecto (razão entre base e altura) de um canal trapezoidal com taludes 2,5H:1V para que haja a máxima eficiência hidráulica?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Para a proporção entre comprimento e altura do talude do enunciado, $$Z=2,5.$$

Pela equação 13, a condição de máxima eficiência, que corresponde ao mínimo perímetro molhado, é obtida por:

$m = \frac{b}{y} = 2 (\sqrt{1 + Z ²} - Z) = 2 (\sqrt{1 + (2,5) ²} - 2,5) = 0,38$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Ou seja, a base deve ser $$b=0,38\ y.$$

Mão na Massa

Teoria na prática

Um canal deverá ser dimensionado para drenagem de uma área de 14.400m², considerando intensidade de chuva de 50mm/h. O conduto terá um comprimento de 150m, estando a montante na cota 15,56m e a jusante em 15,50m, com uma declividade constante. Após um estudo de compatibilidade com a planta urbanística do local, foi estabelecida a seção a seguir, que será revestida com concreto em boas condições. Dimensione a altura da seção para que haja uma folga de 20%.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

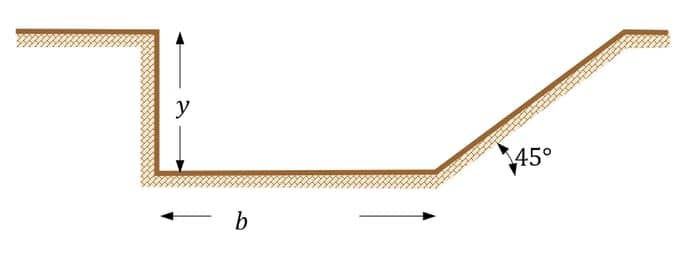
Dimensionamento de seções

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 2

Analisar o escoamento em condutos livres por meio da energia específica

Energia específica

Energia específica e ressalto hidráulico

A carga (energia) do fluido numa seção i do canal é obtida por:

$H_{i} = z_{i} + \frac{p_{i}}{γ} + α \frac{V_{i}^{2}}{2 g}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$z_i$$ e $$p_i$$ são a cota e a pressão no fundo e $$V_i$$ é a velocidade média ao longo da seção. Considerando uma distribuição hidrostática de pressão, $$p_i=\gamma y_i.$$ Além disso, para canais prismáticos, o coeficiente de correção da carga cinética $$\alpha\cong1,$$ então:

$H_{i} = z_{i} + y_{i} + \frac{V_{i}^{2}}{2 g}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Observa-se que, em canais, mesmo no escoamento mais simples possível (permanente e uniforme), $$z_i$$ diminui ao longo do escoamento, consequentemente, $$H_i$$ também. Sendo assim, para simplificar, é adotado o conceito de energia específica, definida por $$E_i=H_i-z_i.$$ A equação anterior pode ser reescrita por:

$E_{i} = y_{i} + \frac{V^{2}}{2 g}$

Equação 15

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A magnitude de $$E,$$ em uma determinada seção do canal, também pode ser definida graficamente, conforme a imagem 15, a seguir:

Imagem 15: Energia específica.

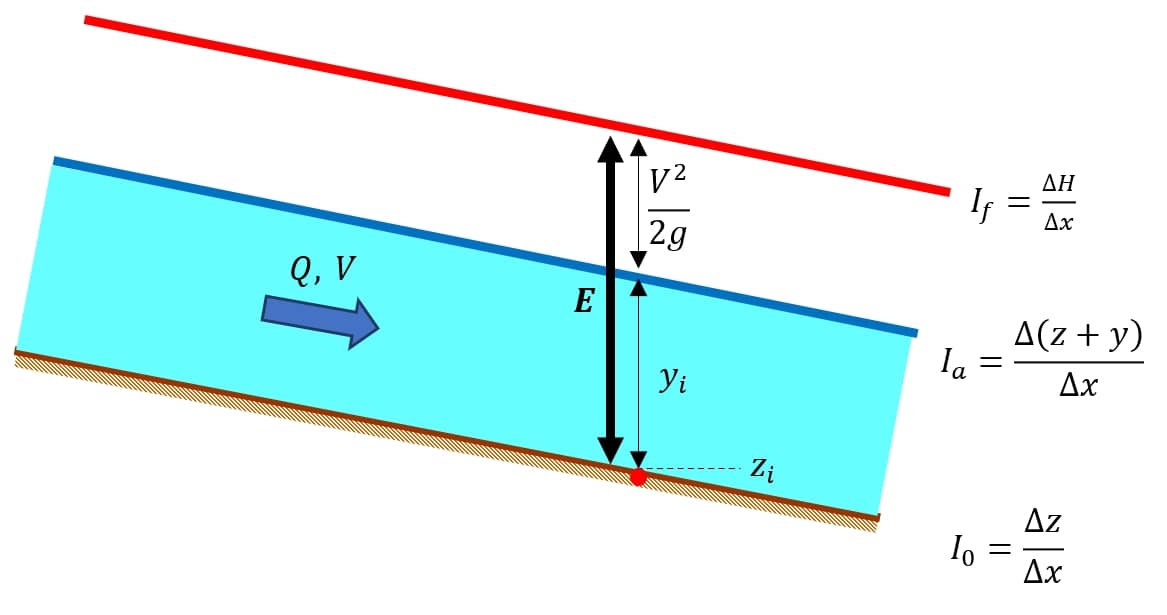
Essa é, então, uma grandeza mais conveniente de se analisar, pois em um escoamento permanente uniforme ($$y$$ e $$V$$ constantes), $$E$$ também será constante.

Conforme vimos no Módulo 1, um dos dados de entrada comum para dimensionamento de canais é a vazão, então a equação anterior pode ser reescrita, substituindo $$V=Q/A:$$

$E_{i} = y_{i} + \frac{Q^{2}}{2 g A^{2}}$

Equação 16

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Curvas de energia para canais retangulares

Para canais retangulares, $$A=by,$$ e a vazão pode ser expressa através da vazão unitária $$q=Q/b.$$ Então:

$E = y + \frac{q^{2}}{2 g y^{2}}$

Equação 17

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$q$$ é medido em m³/s.m.

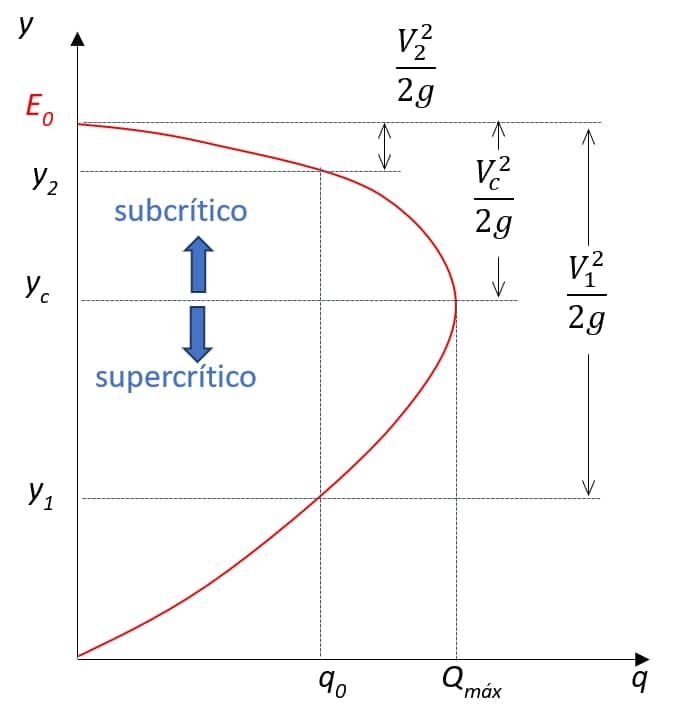
Mantendo-se $$q=q_0$$ constante, podemos traçar o gráfico de $$E=E(y),$$ com base na equação 17, conforme a imagem 16:

Analisando-se o gráfico da imagem 16, observamos aspectos interessantes sobre o escoamento:

Se $y > y_{c} (V < V_{c}) :$ escoamento subcrítico (fluvial), sendo $$y_c$$ a altura crítica, uma redução de $$E$$ (ex.: aumento brusco da cota de fundo) causará uma elevação da altura.
Se $y < y_{c} (V > V_{c}) :$ escoamento supercrítico (torrencial), ocorreria o contrário da afirmação anterior.
Para $y ≅ y_{c} :$ escoamento crítico, pequenas oscilações de $$E$$ causam grandes variações da altura, criando uma região de instabilidade.
Para uma mesma energia específica $$E_o$$ e vazão unitária $$q_0,$$ o escoamento pode ocorrer em duas alturas distintas, $$y_1$$ e $$y_2,$$ chamadas de alturas alternadas.
Para que uma determinada vazão unitária $$q_0$$ seja possível, é necessária uma energia específica mínima $$E_c$$ (crítica).

O valor mínimo de E ocorre quando $$\frac{dE}{dy}=0.$$ Para essa situação, conforme a equação (17), teremos:

$y_{c} = {(\frac{q^{2}}{g})}^{\frac{1}{3}}$

Equação 18

$E_{c} = \frac{3}{2} y_{c}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Lembre-se de que essas equações somente são válidas para canais retangulares. No entanto, as observações ressaltadas sobre o comportamento do escoamento servem para a maioria das seções utilizadas em projetos de canais.

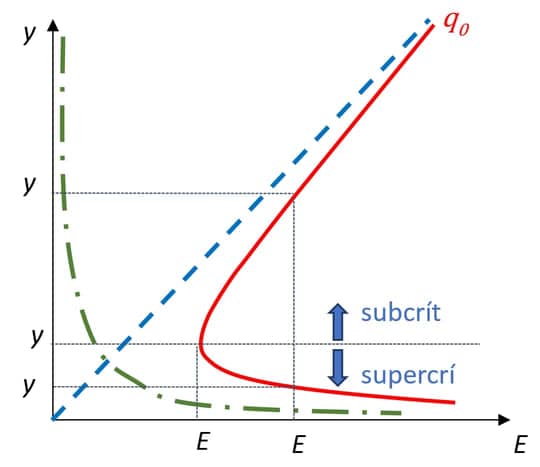
Também podemos inverter a equação 17, explicitando $$q$$ em função de $$y,$$ para então obter o gráfico da imagem 17.

Por esse gráfico, também constatamos que:

Para uma determinada energia específica disponível $$E_0,$$ a vazão máxima que pode ocorrer será:

$q_{m a x} = \sqrt{\frac{8 g}{27}} \sqrt{E_{0}}$

Equação 19

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Se $y < y_{c} :$ escoamento supercrítico (torrencial), um aumento de q causará aumento de $$y.$$
Se $y > y_{c} :$ escoamento subcrítico (fluvial), teremos o contrário da afirmação anterior.

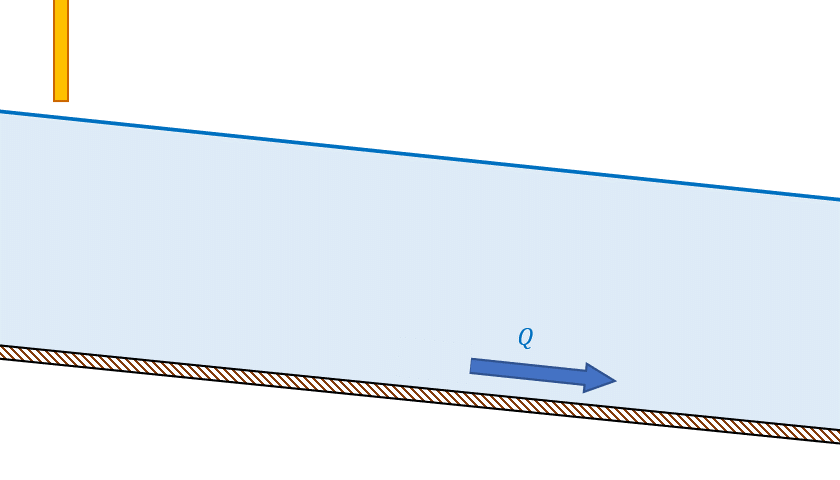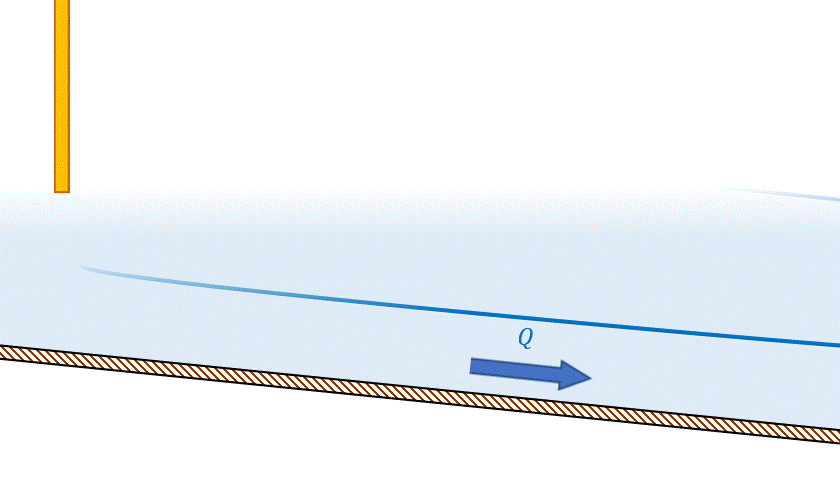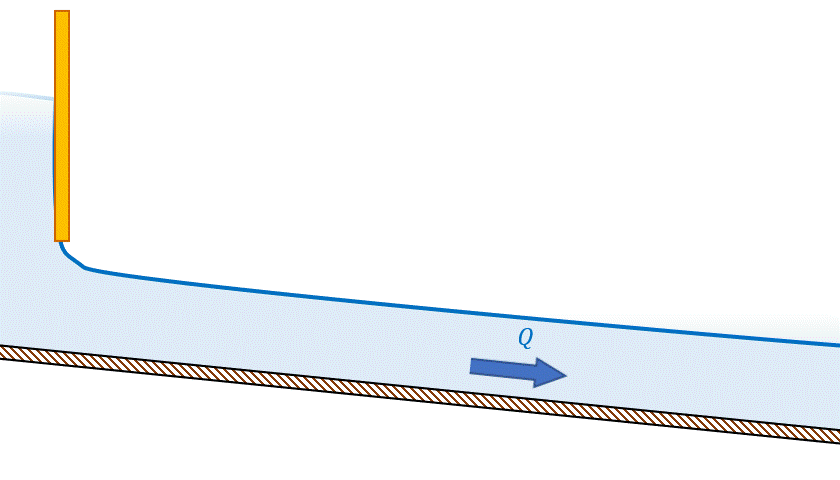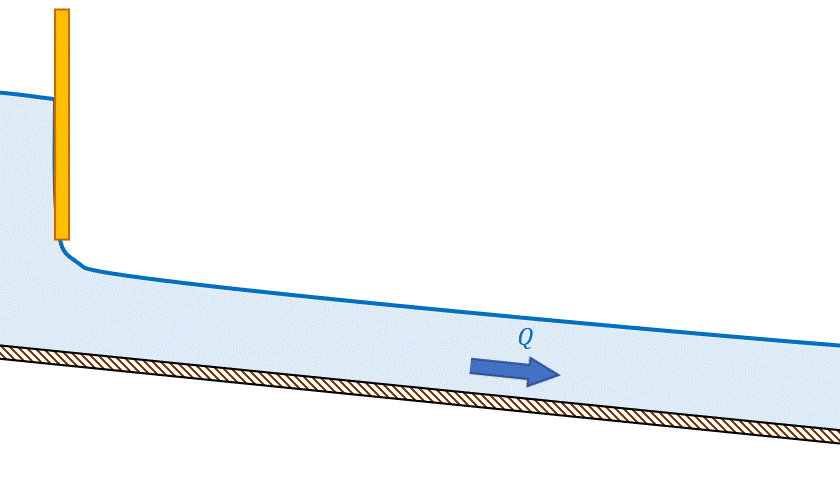
Escoamento subcrítico é influenciado pela condição de jusante: nesse regime, uma redução de vazão é acompanhada de aumento do nível d’água, o que ocorreria se uma comporta na jusante fosse parcialmente fechada, como podemos ver na imagem 18.

Imagem 18: Fechamento de comporta a jusante.

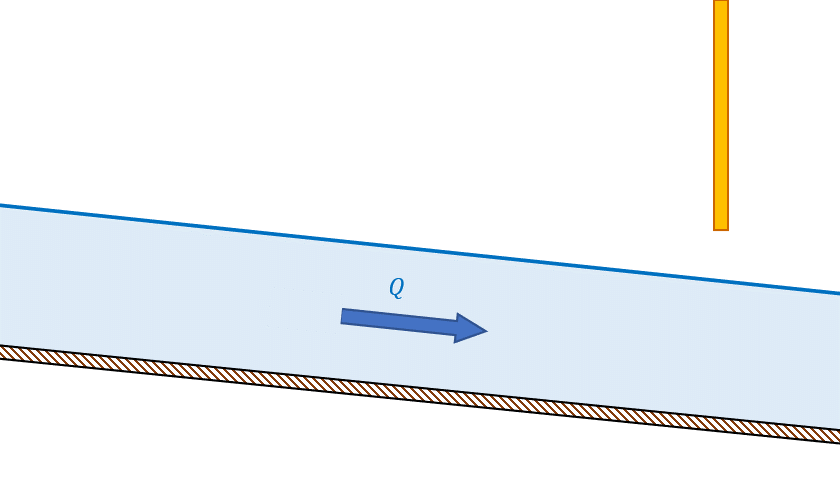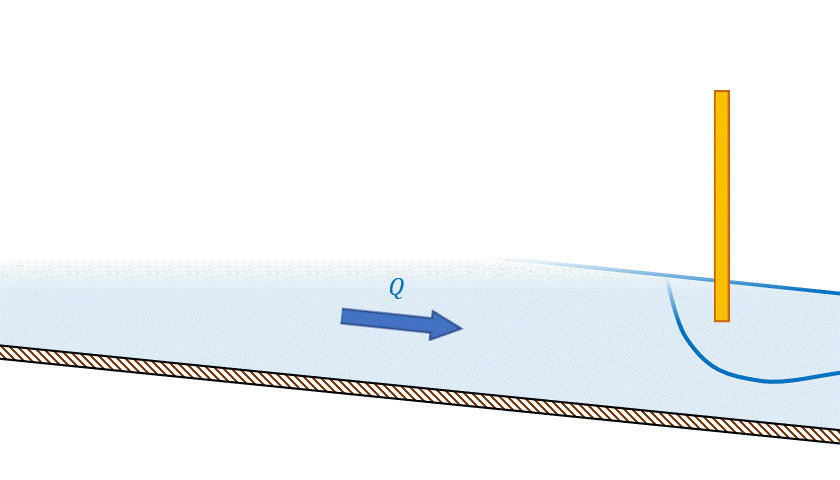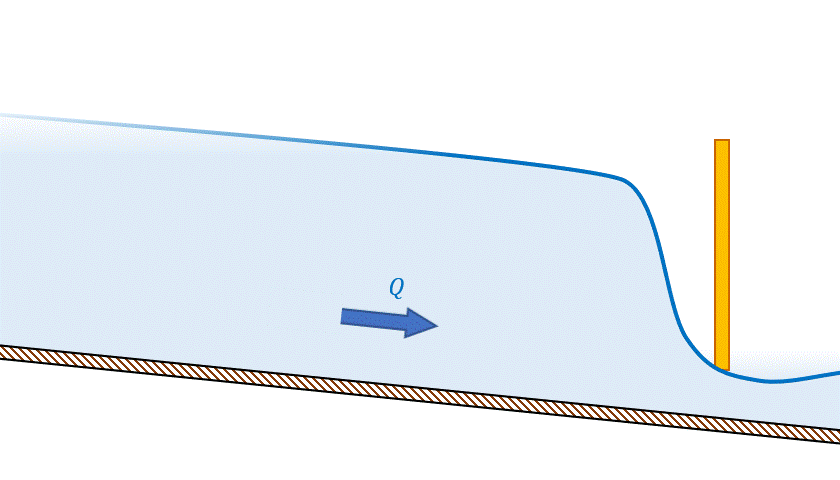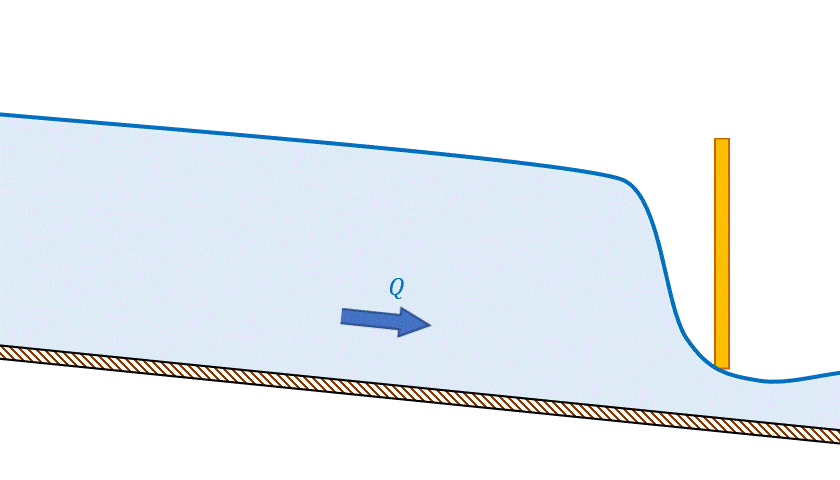
Escoamento supercrítico é influenciado pela condição de montante: nesse regime, uma redução de vazão é acompanhada de redução do nível d’água, o que ocorreria se uma comporta na montante fosse parcialmente fechada (Figura 19).

Imagem 19: Fechamento de comporta a montante.

Estado crítico

Sabemos do cálculo que o máximo ou mínimo de uma função pode ser obtido igualando-se sua derivada à zero. Calculando-se o estado crítico ($$E$$ mínimo ou $$Q$$ máximo) para qualquer tipo de seção, com base na equação 16:

$\frac{d E}{d y} = 0 \to 1 - 2 \frac{Q^{2}}{2 g A^{3}} \frac{d A}{d y} = 0 \to \frac{Q^{2}}{g A^{3}} \frac{d A}{d y} = 1$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O incremento infinitesimal da área pode ser calculado com base na largura de topo, por $$dA=B\ dy.$$ Então:

$\frac{Q^{2}}{g A^{3}} B = 1$

Equação 20

$\to \frac{{(Q / A)}^{2}}{g A} B = 1 \to \frac{V^{2}}{g \frac{A}{B}} = 1$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Substituindo a altura hidráulica (ou média) $$H_m=A/B:$$

$\to \frac{V^{2}}{g H_{m}} = 1 \to \frac{V}{\sqrt{g H_{m}}} = 1$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O termo da esquerda dessa equação é substituído por:

$F r = \frac{V}{\sqrt{g H_{m}}}$

Equação 21

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde Fr é o número de Froude. Se:

$F r = 1 :$ escoamento crítico.
$F r > 1 :$ escoamento supercrítico ou torrencial.
$F r < 1 :$ escoamento subcrítico ou fluvial.

Em caso de canal retangular, $$H_m=\frac{A}{B}=\frac{by}{b}=y.$$ Substituindo-se essa relação para $$Fr=1$$ e na fórmula de Manning, obtemos a declividade crítica, ou seja, para qual ocorre escoamento crítico em regime permanente uniforme:

$I_{c} = n^{2} g y_{c} {(\frac{2 y_{c} + b}{y_{c} b})}^{4 / 3}$

Equação 22

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde a altura crítica $$y_c$$ é obtida pela equação 18.

Vamos ver um exemplo.

Exemplo 7

Um canal retangular tem 2m de largura e é revestido em concreto com boas condições. Qual deve ser a declividade de fundo para que o escoamento permanente e uniforme de 3,5m³/s ocorra em regime crítico?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Com base na vazão unitária $$q=\frac{Q}{b}=\frac{3,5}{2}=1,75m³/s.m,$$ conforme a equação (18), a altura crítica será:

$y_{c} = {(\frac{q^{2}}{g})}^{\frac{1}{3}} = {[\frac{{(1,75)}^{2}}{9,8}]}^{\frac{1}{3}} = 0,68 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A declividade crítica é obtida pela equação (22), sendo $$n=0,013$$ (Quadro 2):

$I_{c} = n^{2} g y_{c} {(\frac{2 y_{c} + b}{y_{c} b})}^{\frac{4}{3}}$

$= {(0,013)}^{2} \cdot 9,8 \cdot 0,68 {(\frac{2 \cdot 0,68 + 2}{0,68 \cdot 2})}^{\frac{4}{3}} = 0,0038 = 3,8 m / k m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Saiba mais

O cálculo da altura e da velocidade crítica foi demonstrado aqui apenas para canais retangulares. Para outras seções, há gráficos disponibilizados na literatura indicada.

Outra opção é substituir $$A$$ e $$B$$ da equação (20) pelos correspondentes ao da seção considerada, como as equações em (3) para canal trapezoidal ou em (4) para circular. Depois disso, podemos implementar esses cálculos em uma planilha eletrônica (ex.: Excel) e calcular, com ferramentas de otimização (ex.: “Atingir meta”), o valor de y para o qual a equação (20) é atendida.

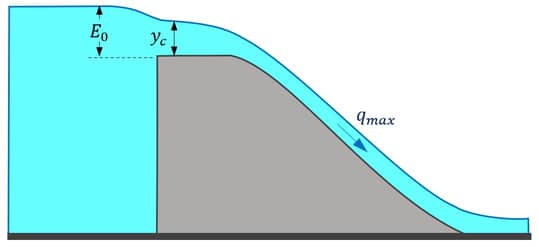
Um exemplo de situação em que pode ocorrer escoamento crítico é em vertedores semelhantes à configuração mostrada na imagem 20. No reservatório, a velocidade é nula, e a energia será igual ao N.A. Portanto, a energia específica $$E_0$$ de montante será igual à distância entre o fundo e o N.A. do reservatório, conforme a definição vista em Energia específica.

Considerando um pequeno trecho até a descida d’água, a perda de carga será desprezível. O escoamento tenderá a ocorrer na máxima vazão possível $$(q_{max}).$$ Conforme visto pelo gráfico da imagem 17, isso corresponde ao ponto de escoamento crítico.

Outra situação comum é quanto ocorre a transição do escoamento subcrítico para crítico, passando pelo crítico em um ponto intermediário, o que é exemplificado em canais de forte declividade $$(I_0>I_c)$$ alimentados por reservatórios.

Transições – elevação de fundo e contração lateral

Elevação de fundo

Com base na definição de energia específica que vimos em Energia específica, assumindo que não há perda de carga significativa ($$H$$ constante), uma elevação de fundo reduzirá a distância entre o N.A. e o fundo, reduzindo também $$E$$ (imagem 15).

Já avaliamos, em Curvas de energia para canais retangulares, a consequência da variação de $$E$$ para uma vazão unitária constante (vazão e largura constantes), tanto para regime subcrítico quanto para supercrítico.

Veremos, agora, a consequência disso no aspecto do escoamento, conforme a imagem 21:

Imagem 21: Elevação de fundo.

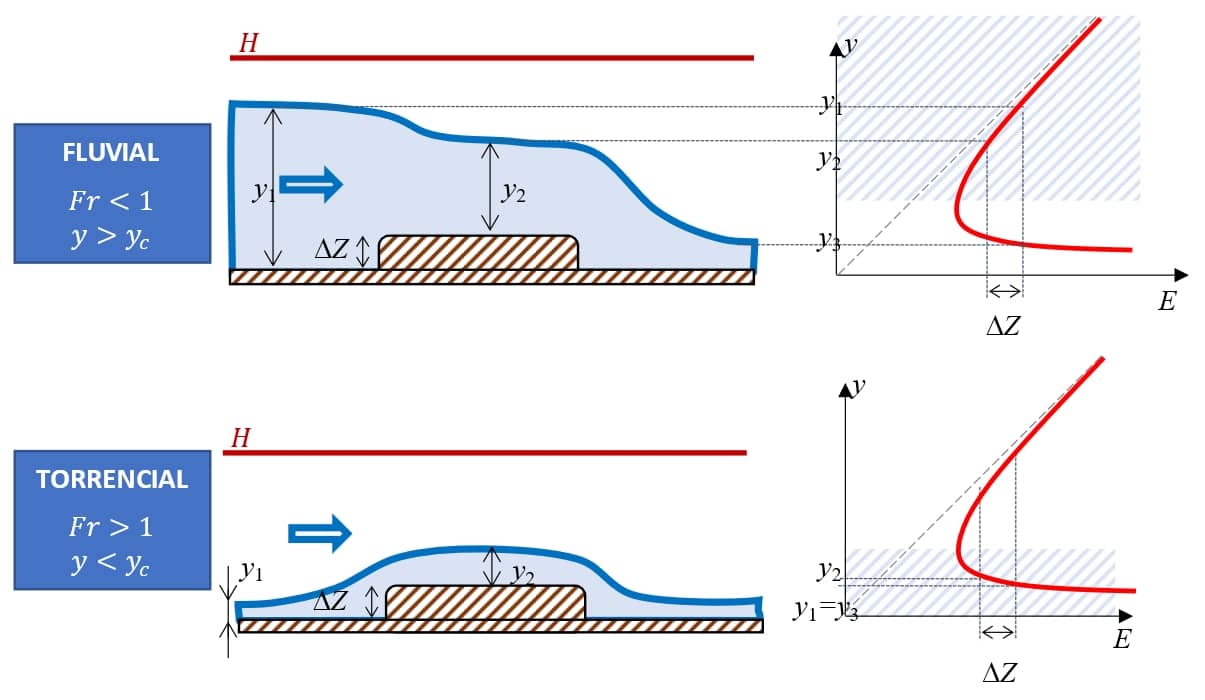
No caso de escoamento fluvial, a elevação de fundo causará redução do nível d’água. Se o $$\Delta Z$$ for suficiente, o regime crítico será atingido e, após a elevação, o escoamento caminhará para o regime supercrítico $$(y_3).$$ No entanto, essa será uma situação momentânea, forçada pela queda após a elevação. Mais adiante, o escoamento voltará para situação de equilíbrio, que ocorria antes da elevação (subcrítico, $$y_1$$).

Se a elevação de fundo forçar uma redução de $$E$$ a ponto de ficar abaixo do $$E_c$$ (energia mínima), sabemos que isso não será possível, portanto, haverá uma alteração do escoamento para montante da seção analisada, causando uma nova condição com maior energia específica.

Em caso de escoamento torrencial, o degrau causará um aumento do N.A., que voltará ao seu nível anterior após a elevação de fundo.

Contração lateral

Em caso de contração lateral da seção do canal, $$q=Q/b$$ aumentará e, assumindo que não há perda de carga, o $$E$$ se manterá constante.

A consequência disso para o escoamento fluvial e torrencial é constatada pelo gráfico da imagem 17 e observada na imagem 22.

Imagem 22: Contração lateral (redução de largura).

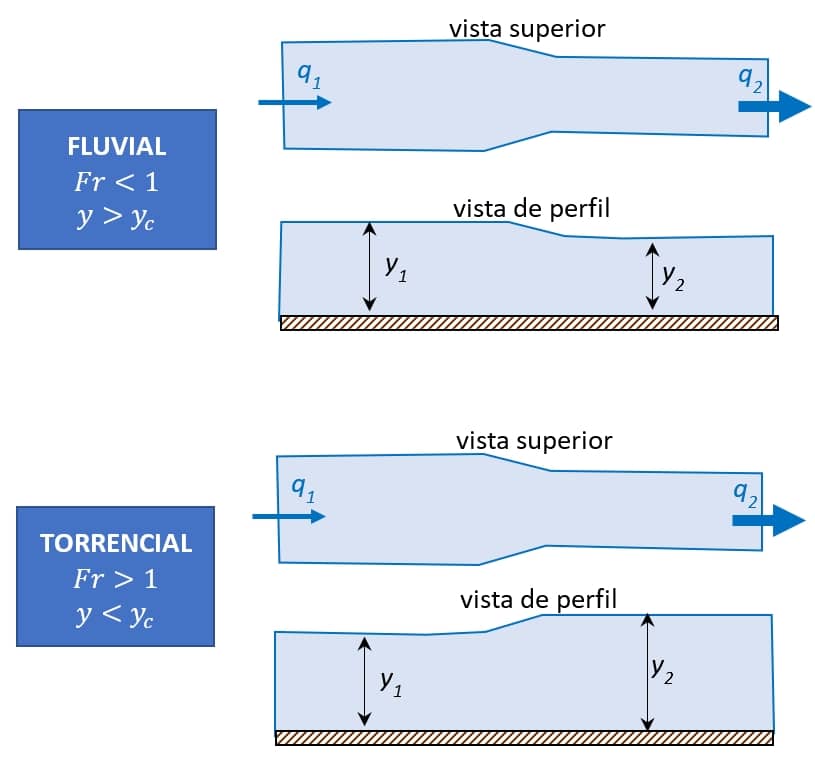
Assim como na elevação de fundo, se a contração lateral (redução de largura) tende a levar a uma condição em que a vazão unitária é superior à máxima, isso não será possível e haverá uma alteração das condições do escoamento, o que se propagará para montante. Atingindo, assim, um nível de energia específica em que seja possível alcançar o valor de $$q$$ imposto pela redução de largura.

Ressalto hidráulico

Ressalto hidráulico é um fenômeno que ocorre quando há a transição do regime supercrítico ou torrencial $$(Fr>1)$$ para o subcrítico ou fluvial $(F r < 1) .$

Imagem 23: Ressalto hidráulico – esquemático.

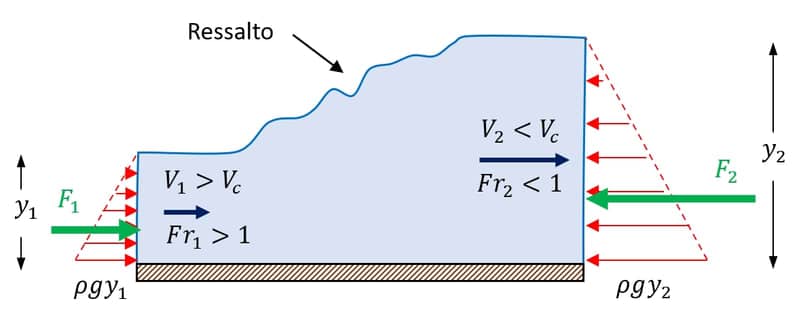
Dependendo do número de Froude a montante $$(Fr_1),$$ essa transição ocorre de maneira brusca, acompanhada de bastante turbulência (imagem 24).

Imagem 24: Tipos de ressalto em função de

F r_{1}

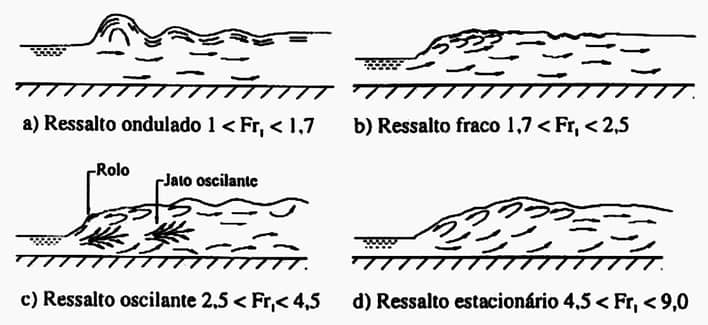
Ressaltos são, muitas vezes, provocados intencionalmente, para dissipação de energia ou mistura de produtos em estações de tratamento de água.

As alturas de água imediatamente antes e após o ressalto são chamadas de alturas conjugadas (não confundir com alturas alternadas!). Para canais retangulares, elas são calculadas por:

$\frac{y_{2}}{y_{1}} = \frac{1}{2} [\sqrt{1 + 8 F r_{1}^{2}} - 1]$

$\frac{y_{1}}{y_{2}} = \frac{1}{2} [\sqrt{1 + 8 F r_{2}^{2}} - 1]$

Equação 23

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Dependendo se a informação conhecida é o nível d’água a montante $$(y_1)$$ ou jusante $$(y_2)$$ do ressalto.

O comprimento do ressalto pode ser estimado a partir da imagem 25, com base no número de Froude da seção de montante $$(Fr_1).$$

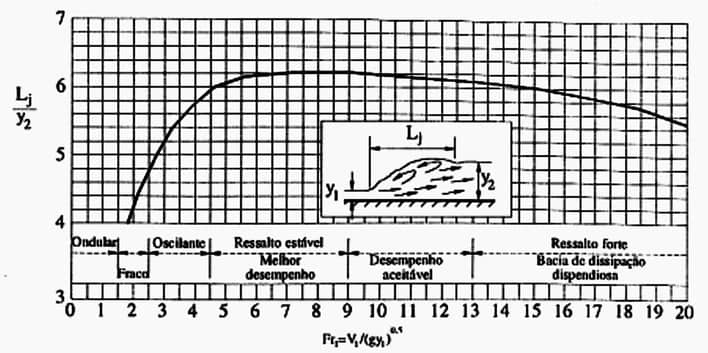
Imagem: Hidráulica Básica. Porto, 2004, pág. 345

Imagem 25: Comprimento do ressalto hidráulico

Como, muitas vezes, os ressaltos são projetados para dissipar energia, a perda obtida é calculada por:

$∆ E = \frac{{(y_{2} - y_{1})}^{3}}{4 y_{2} y_{1}}$

Equação 24

Atenção! Para visualização completa da equação utilize a rolagem horizontal

E a sua eficiência por:

$η = \frac{∆ E}{E_{1}}$

Equação 25

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Vamos ver um exemplo.

Exemplo 8

Uma comporta instalada no fundo da barragem ilustrada na figura a seguir descarrega uma vazão unitária de 2,0m³/m.s em um canal retangular com escoamento supercrítico.

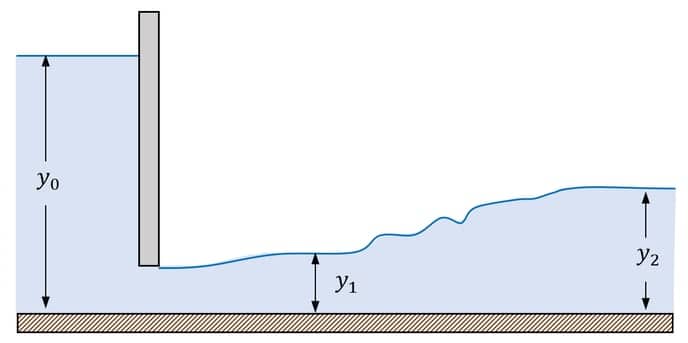
Um ressalto é formado logo após, e a altura a jusante foi medida em $$y_2 = 1,50.$$ Calcule a altura a montante do ressalto.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

A velocidade a jusante do ressalto, lembrando que a vazão unitária é $$q=\frac{Q}{b},$$ é calculada por:

$V_{2} = \frac{Q}{A_{2}} = \frac{Q}{b y_{2}} = \frac{q}{y_{2}}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O número de Froude a jusante do ressalto, para canal retangular, é calculado por:

$F r_{2} = \frac{V_{2}}{\sqrt{g y_{2}}} = \frac{q}{\sqrt{g y_{2}^{3}}} = \frac{2,0}{\sqrt{9,8 \cdot {(1,5)}^{3}}} = 0,348$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela equação 23:

$y_{1} = \frac{y_{2}}{2} [\sqrt{1 + 8 F r_{2}^{2}} - 1] = \frac{1,5}{2} [\sqrt{1 + 8 \cdot {(0,348)}^{2}} - 1] = 0,30 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Portanto, as alturas conjugadas desse ressalto são 0,30m e 1,50m.

Mão na Massa

Teoria na prática

(EPE − Analista de Pesquisa Energética − Projetos da Geração de Energia − 2010) Considere uma bacia de dissipação por ressalto hidráulico construída em um canal retangular largo, por onde escoa a vazão por metro de largura $$q = 5,0m³/s.m.$$ Sabe-se que a altura da lâmina d’água do escoamento a montante do ressalto hidráulico é $$y_1 = 0,50m$$ e o número de Froude é $${Fr}_1= 4,5.$$ O escoamento a jusante do ressalto hidráulico tem altura de lâmina d’água $$y_2\ =\ 2,0m$$ e número de Froude $${Fr}_2 = 0,60.$$ Qual é a potência dissipada por metro de largura do canal, em kW, no ressalto hidráulico?

Dados:

$E = y + \frac{V^{2}}{2 g}$ ; $Q = q \cdot b = V . A$ e $P_{d i s} 10 \cdot Q \cdot h_{p e r d a}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde:

$$E$$ é a energia específica do escoamento (m).
$$y$$ é altura da lâmina d’água ou tirante d’água (m).
$$V$$ é a velocidade do escoamento (m/s) e $$Q$$ é a vazão (m³/s).
$$b$$ é a largura do canal (m) e $$q$$ é a vazão por metro de largura do canal [m³/(s.m)].
$$A$$ é a área molhada da seção transversal (m).
$$g$$ é a aceleração da gravidade (considerar igual a 10m/s²).
$$P_{dis}$$ é a potência dissipada no ressalto hidráulico (kW).
$$h_{perda}$$ é a perda de carga no ressalto hidráulico (m).

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Dissipação de energia em ressalto

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 3

Identificar o perfil do nível d’água em escoamentos variados

Classificações de escoamento não uniforme

Escoamento variado

As equações que vimos no Módulo 1 são fundamentadas na condição de equilíbrio, quando calculamos a altura normal de escoamento $$y_n,$$ ou seja, para a qual as forças de resistência se igualam ao componente da gravidade na direção do escoamento. Naquela situação, o nível d’água é paralelo ao fundo, e o escoamento é classificado como uniforme. Quando o escoamento não é uniforme (variado), a solução das equações da hidrodinâmica se torna complexa, o que requer métodos numéricos ou iterativos. No entanto, com base em características da situação em que o trecho analisado se encontra, é possível prever o formato do perfil d’água de maneira relativamente simples.

O primeiro passo é determinar qual a altura crítica $$y_c$$ e a declividade que provoca essa altura em condição uniforme (de equilíbrio), chamada de declividade crítica $$I_c.$$ Esses parâmetros são obtidos pela solução da equação de Manning para $$Fr=1.$$

O caso de canal retangular foi desenvolvido no Módulo 2, e é o único que apresenta solução analítica direta, fornecendo então:

$y_{c} = {(\frac{q^{2}}{g})}^{\frac{1}{3}}$

$I_{c} = n^{2} g y_{c} {(\frac{2 y_{c} + b}{y_{c} b})}^{4 / 3}$

Equação 26

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Se o canal não for retangular, há gráficos disponíveis na literatura indicada para o cálculo desses parâmetros.

Comparando-se a altura d’água normal $$y_n$$ e a declividade de fundo $$I_0$$ com seus respectivos valores críticos ($$y_c$$ e $$I_c$$), é possível classificar a transição de escoamento em diversas situações.

Quanto à declividade, ela será classificada entre:

$I_{0} > I_{c}$ e $y_{n} < y_{c}$ : declividade forte − S (steep slope).

$$I_0=I_c$$ e $$y_n=y_c:$$ declividade crítica − C (critical slope).

$0 < I_{0} < I_{c}$ e $y_{n} > y_{c}$ : declividade fraca − M (mild slope).

$$I_0=0:$$ horizontal – H (horizontal).

$I_{0} < 0$ : aclive – A (adverse slope).

Embora um canal em aclive (declividade adversa) possa parecer incoerente, pois em canais o escoamento se dá pela gravidade, essa condição pode ocorrer por trechos curtos, onde a quantidade de movimento é capaz de manter o escoamento.

Uma vez definido o tipo de declividade, devemos classificar o trecho analisado em relação ao nível d’água, dividindo-o em três regiões, ordenadas de cima para baixo, conforme o quadro 3:

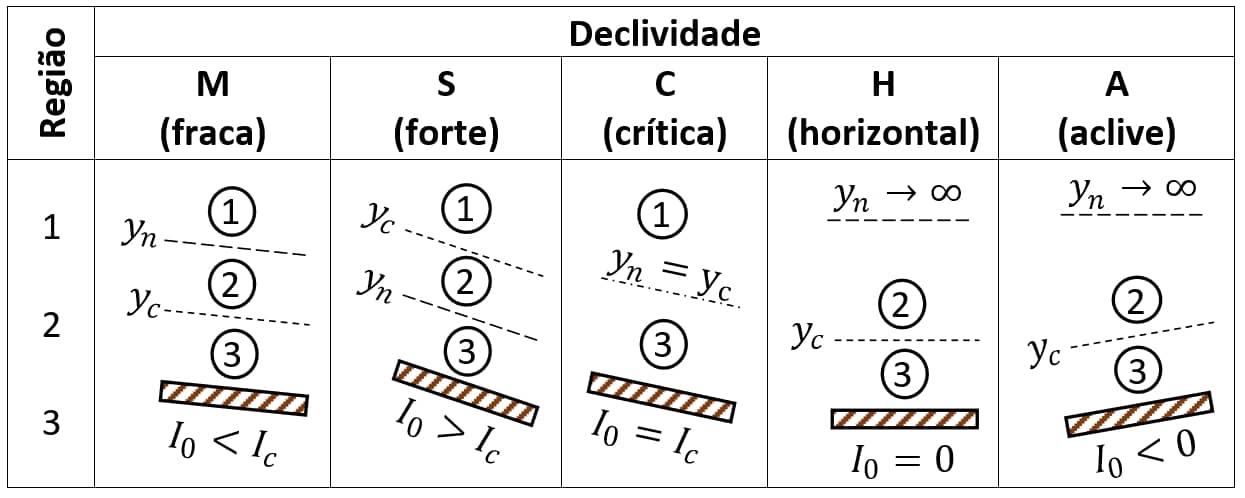
Quadro 3: Classificação quanto a altura d’água para cada tipo de declividade.
Elaborada por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento

Com base na equação de Manning, para declividade nula ou negativa, a altura normal $$y_n$$ tenderá ao infinito, pois não é possível haver um escoamento uniforme (em equilíbrio) nessas situações.

Perfis de escoamento gradualmente variado

Com base nas classificações listadas, é possível prever a forma do perfil d’água, conforme a imagem 26.

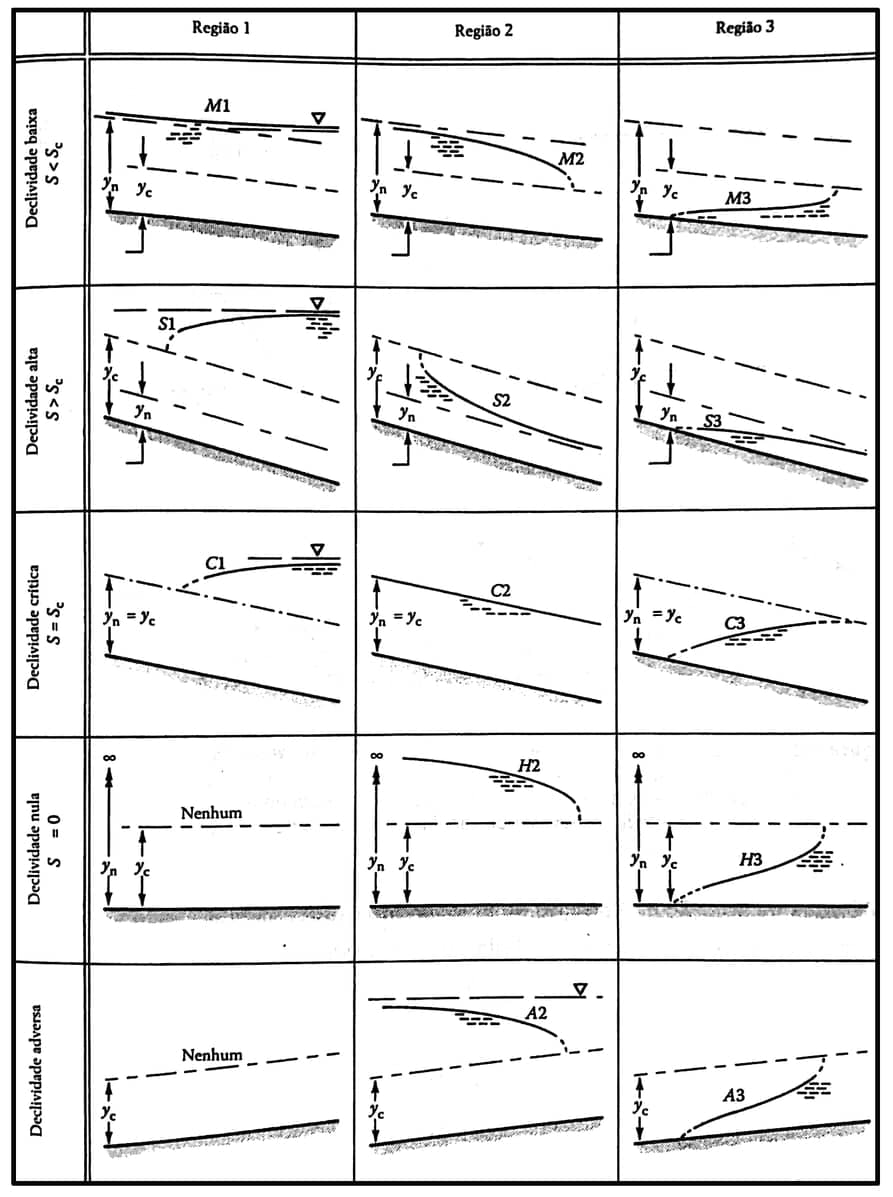
Hidráulica para Engenharia Civil e Ambiental. Chadwick, 2017.

Imagem 26: Perfis de escoamento gradualmente variado.

Conforme vimos no Módulo 2, os escoamentos subcríticos são influenciados pela condição de jusante, enquanto os supercríticos são influenciados pela condição de montante. Portanto, se a altura d’água $$y$$ está diferente da altura normal $$y_n,$$ em um escoamento subcrítico, isso será causado por algo que está na jusante (ex.: barragem) e, em caso de supercrítico, por algo que está no montante (ex.: comporta).

Vamos ver um exemplo.

Exemplo 9

A imagem a seguir mostra um canal aberto com um trecho com declividade fraca (até C) e outro com declividade forte (após C). A altura normal e a altura crítica também são representadas. Há uma comporta parcialmente fechada em B. Faça um esboço no perfil d’água nos trechos AB, BC e CD. Considere que o trecho BC é suficiente logo para que o regime volte a ser uniforme.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

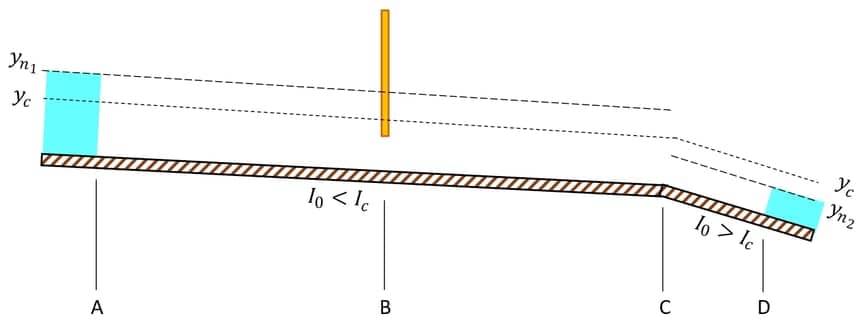
Até A, o escoamento era uniforme e subcrítico $$(y_n>y_c).$$ Sabemos que esse regime é influenciado pela condição de jusante, o que ocorrerá devido à comporta, elevando $$y.$$ Em se tratando de uma declividade fraca com $$y>y_n,$$ teremos a curva M1 (imagem 26).

A comporta causará uma altura menor que $$y_c,$$ forçando um escoamento supercrítico. Como o trecho $$BC$$ é suficiente longo para que o escoamento volte a ser subcrítico (uniforme), haverá um ressalto hidráulico (transição de supercrítico para subcrítico, conforme vimos no Módulo 2, Transições – elevação de fundo e contração lateral) em algum ponto.

Ressalto hidráulico é um escoamento bruscamente variado, porém, até chegar nele, haverá uma variação desde a altura imposta pela comporta até a altura de montante do ressalto. Nessa transição, temos um trecho de fraca declividade, com $y < y_{c}$ classificado, então, como M3 (imagem 26).

Após o ressalto, a altura voltará a ser $$y_n.$$ Se aproximando mais de $$C,$$ teremos uma redução dessa altura causada pela transição da declividade. Ou seja, $y_{c} < y < y_{n}$ ainda com declividade fraca, o que é classificado como curva M2 (imagem 26).

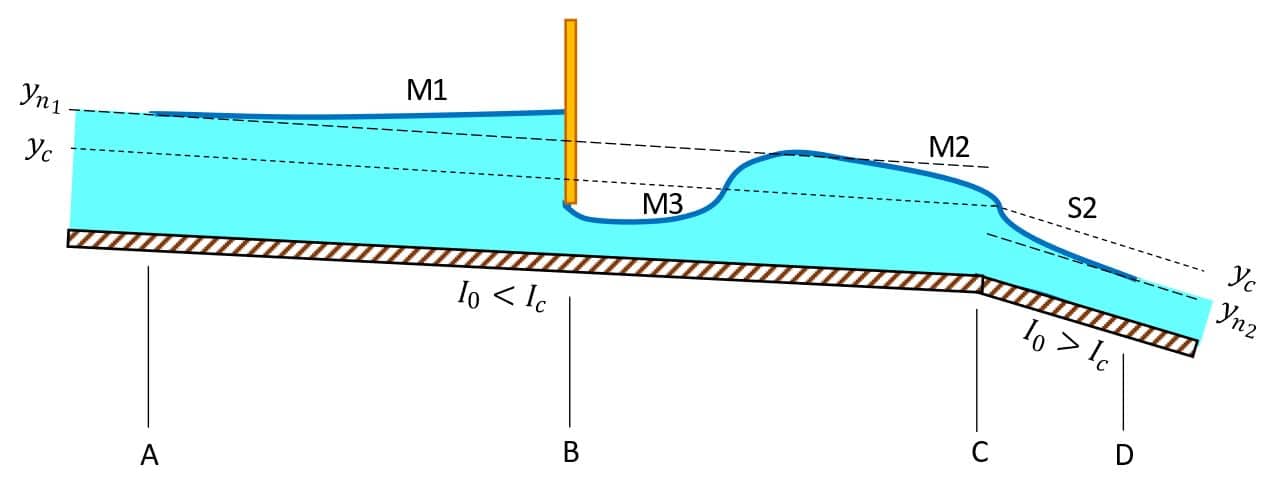
Por fim, teremos em CD uma declividade forte e um escoamento supercrítico, que é influenciado pela condição de montante, vindo então de $$y>y_c.$$ Essa condição corresponde à classificação de curva S2 (imagem 26).

O resultado do perfil com base nas classificações das curvas obtidas (M1, M3, M2 e S2) de acordo com a imagem 26 é exibido na figura a seguir.

Cálculo do perfil d’água

Conforme vimos no Módulo 2, a energia específica é definida como a distância entre o fundo do canal $$y_0$$ e o nível de energia $$y_f,$$ portanto:

$E = y_{f} - y_{0} \to \frac{d E}{d x} = \overset{- I_{f}}{\overset{⏞}{\frac{d y_{f}}{d x}}} - \overset{- I_{0}}{\overset{⏞}{\frac{d y_{0}}{d x}}}$

$\to d x = \frac{d E}{I_{0} - I_{f}}$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Esse cálculo pode ser resolvido, aproximadamente, pelo método das diferenças finitas (MEF) entre os pontos 1 e 2 consecutivos:

$Δ x = \frac{E_{2} - E_{1}}{I_{0} - {\bar{I}}_{f}}$

Equação 27

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como a declividade da linha de energia $$I_f$$ pode variar entre os pontos, adotamos o valor médio $${\bar{I}}_f$$ calculado pela equação de Manning com base na altura média $$\bar{y}.$$ Para canal retangular, a partir das equações abordadas no Módulo 1, temos:

$I_{f} = n^{2} q^{2} {(\frac{b + 2 y}{y^{5 / 2} b})}^{4 / 3}$

Equação 28

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A estratégia de cálculo consiste em partir da altura $$y$$ de jusante, obtendo a energia do ponto anterior, $$\Delta y$$ (a seguir), e calculando o incremento $$\Delta x$$ pela equação 27. Sendo assim, a cada passo, as coordenadas $$x$$ e $$y$$ de um ponto são obtidas.

Exemplo 10

Um canal retangular com 2,00m de largura tem $$n=0,013,$$ declividade de fundo de 2m/km e transporta um escoamento de 3,0m³/s. Calcule o perfil d’água do remanso causado por uma comporta de fundo que eleva a altura uniforme de 0,76m para 0,90m.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Iniciaremos nosso cálculo pela altura junto à comporta. Para cada ponto a montante, calcularemos a altura média, a energia específica (17) e sua variação, a declividade energética (28) e o incremento da posição $$x,$$ através da equação 27.

A declividade e a altura crítica são obtidas por (26):

$$y_c=0,61m $$ e $$I_c=0,0037m.$$

Como $I_{0} < I_{c}$ , trata-se de uma declividade fraca. Além disso, $$y>y_n>y_c,$$ o que classifica essa curva como M1.

O cálculo desse exemplo é detalhado no quadro 4, partindo-se de $$y_0=0,90m$$ e adotando-se $$\Delta y=-0,02m.$$ A cada passo, a energia específica é calculada conforme a equação 17 e o incremento $$\Delta x$$ pela equação 27.

$$y$$ (m)	$y_{m e d}$ (m)	$$E$$ (m)	$$\Delta E$$ (m)	$${\bar{I}}_f$$ (m/m)	$$\Delta x$$ (m)	$$x$$ (m)
0.90		1.042				0
0.88	0.89	1.028	-0.0140	0.00131	-20.29	-20.29
0.86	0.87	1.015	-0.0130	0.001394	-21.45	-41.74
0.84	0.85	1.003	-0.0120	0.001484	-23.26	-65.00
0.82	0.83	0.991	-0.0120	0.001584	-28.85	-93.85
0.80	0.81	0.979	-0.0120	0.001693	-39.09	-132.94
0.78	0.79	0.969	-0.0100	0.001813	-53.48	-186.42
0.76	0.77	0.959	-0.0100	0.001946	-185.19	-371.61

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 4: Cálculo do perfil d’água pelo step method.
Elaborado por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento

Na imagem a seguir, vemos o gráfico resultante. Percebe-se que se assemelha à curva M1.

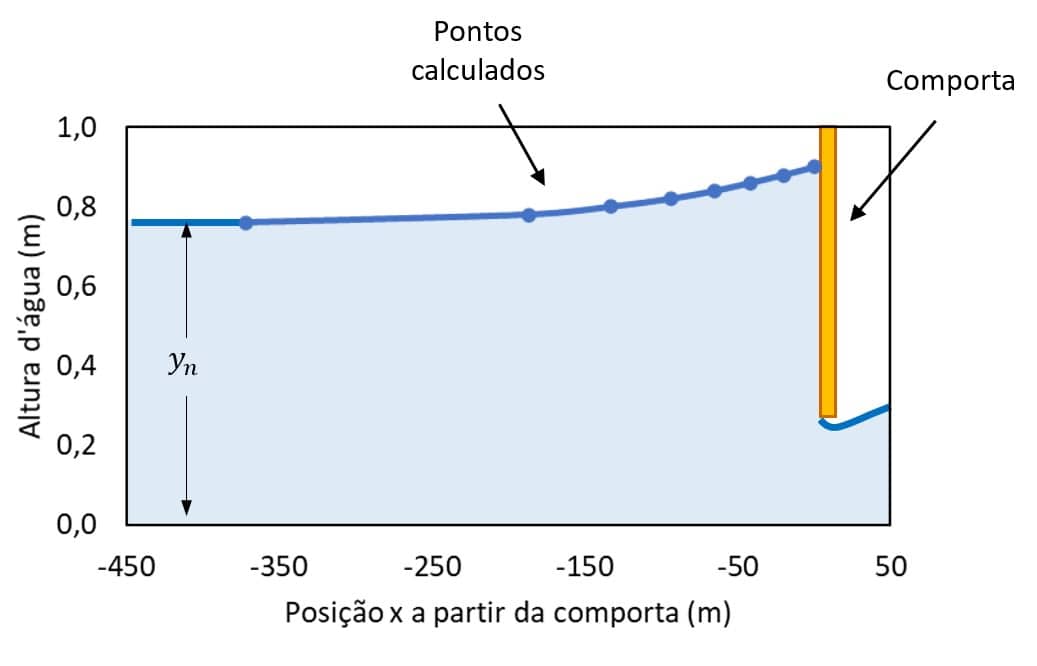
Observe que o remanso, nesse caso, se estendeu até 371,6m a montante da comporta.

Por se tratar de uma solução numérica (MDF), quanto menor o incremento $$\Delta y$$ adotado, mais preciso será o resultado.

Ondas de translação

Mudanças bruscas no escoamento de montante, para regime supercrítico, ou no de jusante, para subcrítico, tendem a provocar ondas que se propagarão ao longo do canal.

Essas ondas podem ser positivas, em caso de elevação do N.A., ou negativas, caso contrário, como podemos ver no quadro 5, a seguir.

	Montante	Jusante
Positiva
Negativa

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 5: Classificação das ondas de translação.
Elaborado por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento

A celeridade $$c$$ é definida como a velocidade de propagação da onda ao longo de um canal em relação à velocidade de escoamento. Sua dedução é feita com base na equação da continuidade e da quantidade de movimento. Para canais retangulares, será:

$c = \sqrt{\frac{g y_{2}}{2 y_{1}} (y_{1} + y_{2})}$

Equação 29

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Onde $$y_1$$ é a altura do escoamento não perturbado, ou seja, antes da onda, e $$y_2$$ é a altura resultante após a passagem da onda.

É importante ressaltar que a celeridade é a velocidade de propagação da onda em relação à do escoamento $$V_1,$$ portanto, para obter a velocidade absoluta da onda $$V_\omega$$ (em relação ao solo), devemos utilizar o conceito de velocidade relativa. Sendo assim:

$V_{ω} = V_{1} \pm c$

Equação 30

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Sendo $$c$$ somado em caso de onda de montante e subtraído em caso de onda de jusante (quadro 5).

Vamos ver um exemplo.

Exemplo 11

O colapso de uma barragem fez com que a altura d’água em um rio com escoamento a 1,5m/s elevasse subitamente de 1,20m para 2,00m, provocando uma onda de cheia. Calcule quanto tempo levará para ela alcançar um vilarejo às margens desse rio cerca de 1,0km a jusante da barragem.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Dados de entrada:

$$y_1=1,20m:$$ altura d’água não perturbada.
$$V_1=1,50m:$$ velocidade não pertubada.
$$y_2=2,00m:$$ altura com a onda.
$$L=1,0km = 1000 m:$$ distância a ser percorrida.

A celeridade é (29):

$c = \sqrt{\frac{g y_{2}}{2 y_{1}} (y_{1} + y_{2})} = \sqrt{\frac{9,8 \cdot 2,0}{2 \cdot 1,2} (1,2 + 2,0)} = 5,11 m / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como se trata de uma onda de montante, a velocidade da onda de cheia será (30):

$V_{ω} = V_{1} + c = 1,5 + 5,11 = 6,61 m / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

O tempo para alcançar o vilarejo será:

$Δ t = \frac{Δ S}{V_{ω}} = \frac{1000}{6,61} = 151 s = 2 m i n e 31 s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Mão na Massa

Teoria na prática

Um canal deverá ser projetado para escoar água do exutório de uma bacia com 117 hectares no caso extremo de 80mm/h de chuva. A topografia impões duas declividades em trechos distintos, conforme representado na figura a seguir.

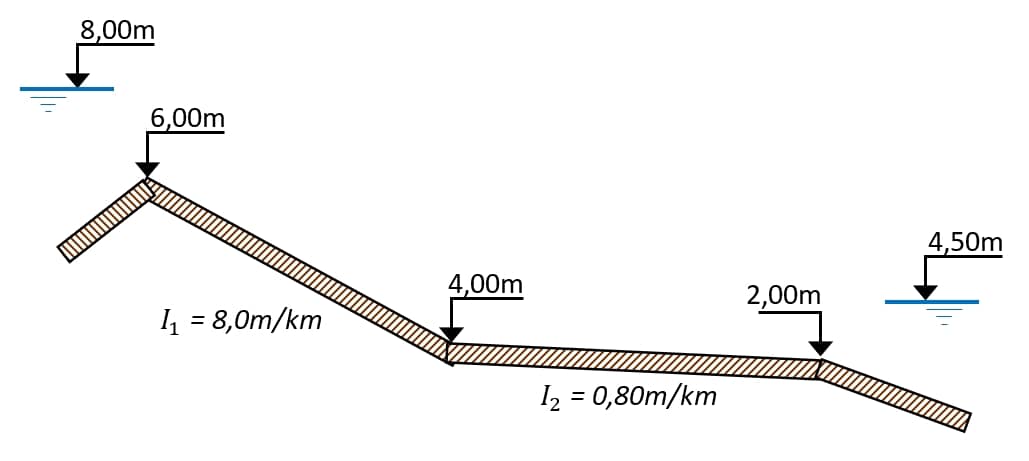
A profundidade da calha das seções deverá ser suficiente para que comporte a altura d’água, por isso é necessário prever o esboço perfil ao longo de todo o canal.

Assuma que:

o revestimento é de concreto em condições regulares;
os trechos são suficientemente longos para que seja alcançado o regime uniforme;
o tempo de chuva é suficiente para que o regime permanente seja alcançado.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Perfil d’água em escoamento gradualmente variado

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

MÓDULO 4

Reconhecer a performance de seções compostas

Observações

Seções compostas

Conforme observamos, há muitos parâmetros envolvidos no projeto de canais, o que pode permitir diferentes soluções de dimensionamento para uma mesma demanda. No entanto, há diversos detalhes que devem ser atentados, entre eles, alguns que acabam restringindo ou recomendando uma faixa de valores mais adequados.

Listaremos a seguir algumas das principais observações que devem ser atentadas, conforme destacado por Porto (2004):

Clique nas barras para ver as informações. Objeto com interação.

1. Construção

A construção do canal deve ser feita, se possível, da jusante para montante, o que permite trabalhar no “seco”, em caso de novo canal, ou em vazões mais baixas, em caso de alargamento de canal existente.

2. Incertezas quanto à rugosidade

Devido às incertezas quanto à rugosidade e ao envelhecimento do revestimento, recomenda-se adotar valores de $$n$$ 15% maiores que os encontrados na literatura.

3. Incertezas quanto à vazão

Devido às incertezas quanto à vazão que deverá ser transportada na situação mais crítica, recomenda-se deixar uma folga de segurança de 20% a 30% entre o nível d’água e o topo da seção.

4. Profundidade

A profundidade de escavação ficará limitada às condições geotécnicas do local, o que deve ser avaliado antes do dimensionamento do canal.

5. Canais com revestimento de baixa permeabilidade

Em canais com revestimento de baixa permeabilidade (ex.: concreto), devem ser instalados drenos para evitar o acúmulo de água no solo, o que causaria aumento de poropressão e, eventualmente, danificaria o revestimento.

6. Canais com revestimento rígido

Em canais com revestimento rígido, devem ser instaladas juntas de dilatação, para acomodar a deformação causada pelos ciclos de aquecimento e resfriamento diários.

7. Retificação de canais

A retificação de canais se traduz em redução do comprimento e, consequentemente, maior declividade de fundo, causando aumento da velocidade e, possivelmente, erosão do revestimento. Além disso, a maior velocidade pode causar impactos negativos em trechos a jusante.

8. Velocidade

A velocidade deve ter um valor mínimo para evitar a sedimentação de material na calha do canal, o que, em longo prazo, reduz a seção útil de escoamento. Por outro lado, velocidades muito elevadas podem causar erosão. Sendo assim, é possível encontrar na literatura faixa de valores recomendados (quadro 6).

Material	Velocidade média (m/s)
Areia muito fina	0,23 a 0,30
Areia solta-média	0,30 a 0,46
Areia grossa	0,46 a 0,61
Terreno arenoso comum	0,61 a 0,76
Terreno silte-argiloso	0,76 a 0,84
Terreno de aluvião	0,84 a 0,91
Terreno argiloso-compacto	0,91 a 1,14
Terreno argiloso duro	1,14 a 1,22
Solo cascalhado	1,22 a 1,52
Cascalho grosso, pedregulho, piçarra	1,52 a 1,83
Rochas sedimentares moles-xistos	1,83 a 2,44
Alvenaria	2,44 a 3,05
Rochas compactas	3,05 a 4,00
Concreto	4,00 a 6,00

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 6: Recomendações de faixas de velocidade.
Extraída de Porto(2004).

9. Talude vertical

Quanto mais vertical for o talude, maior será a área disponível e, consequentemente, maior a capacidade de escoamento. No entanto, essa declividade fica sujeita à estabilidade, o que depende do tipo de solo. No quadro 7, são apresentados alguns valores usuais.

Natureza das paredes	Z
Canais em terra em geral, sem revestimento	2,5 a 5,0
Canais em saibro, terra porosa	2,00
Cascalho roliço	1,75
Terra compacta, sem revestimento	1,50
Terra muito compacta, paredes rochosas	1,25
Rochas estratificadas, alvenaria de pedra bruta	0,50
Rochas compactas, alvenaria acabada, em concreto	0,00

Atenção! Para visualização completa da tabela utilize a rolagem horizontal

Quadro 7 – Valores usuais para inclinação de taludes.
Extraída de Azevedo Netto (1998)

Seções com revestimento composto

Muitas vezes, a rugosidade do revestimento não é a mesma ao longo da seção (ex.: taludes em material diferente do fundo). Nesse caso, será necessário calcular um valor único equivalente do coeficiente de Manning, com base em $$N$$ trechos de perímetro molhado e suas respectivas rugosidades $$n_i.$$

Considerando que a força total de resistência (cisalhamento) é igual à soma em cada trecho de perímetro molhado, a rugosidade equivalente é calculada por:

$n_{e} = \sqrt{\frac{\sum_{i = 1}^{N} (P_{i} {n_{i}}^{2})}{P}}$

Equação 31

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Vamos ver um exemplo.

Exemplo 12

Determine a capacidade de vazão de um canal para drenagem urbana, com 2,0m de base e 1,0m de altura d’água, declividade de fundo igual a $I_{o} = 0,001 m / m$ e taludes 1,5H:1V. O fundo corresponde a canal dragado em condições regulares, $$n = 0,030,$$ e os taludes são de alvenaria de pedra aparelhada em boas condições, $$n = 0,014.$$ Essa seção é de mínimo perímetro molhado?

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Da equação 32, a rugosidade equivalente da seção é dada por:

$n_{e} = \sqrt{\frac{P_{1} \cdot n_{1}^{2} + P_{2} \cdot n_{2}^{2}}{P_{1} + P_{2}}} = \sqrt{\frac{2,0 \cdot 0 {,030}^{2} + 2 \cdot 1,80 \cdot 0 {,014}^{2}}{2,0 + 1,80}} = 0,021$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela fórmula de Manning 7:

$Q = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2} = 3,85 m^{3} / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Para máxima eficiência hidráulica (mínimo perímetro molhado), conforme a equação 13:

$m = 2 (\sqrt{1 + Z ²} - Z) = 2 (\sqrt{1 + 1,5 ²} - 1,5) = 0,65 \neq 2$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Como o mínimo perímetro molhado (0,65m) é muito diferente do $$P$$ informado pelo enunciado, essa não é uma seção hidraulicamente eficiente.

Seções com geometria composta

A vazão em canais sofre uma grande variação entre a condição fluvial e a pluvial, ou seja, quando a chuva intensa provoca escoamentos com vazões muito superiores. Isso resulta numa dificuldade de se alcançar os limites de velocidade adequados (quadro 6). Para contornar isso, uma solução inteligente consiste em dimensionar uma seção menor, para garantir velocidade adequada em baixas vazões, e um leito secundário, que é preenchido nas cheias.

Para avaliar esse tipo de situação, dividimos em subáreas, calculando a vazão em cada uma pela equação de Manning, contabilizando como perímetro molhado apenas onde há contato de água com revestimento, ou seja, desconsiderando segmentos entre subáreas (linha GD na imagem 28). Por fim, a vazão total é obtida pela soma da calculada em cada subárea.

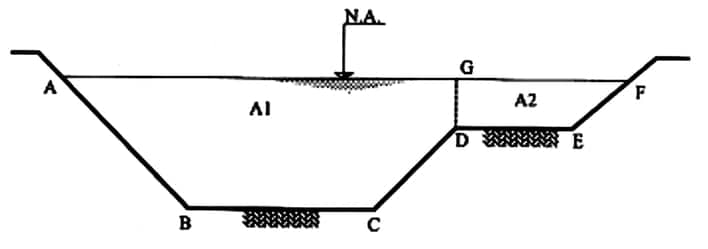
Hidráulica Básica. Porto, 2006, pág. 277.

Imagem 28: Seção com geometria composta.

No exemplo da imagem 28:

Clique nas informações a seguir. Clique nas informações a seguir.

Subárea A1

Subárea A2

Subárea A1

Calcularíamos a área $$A_1$$ de ABCDG e o perímetro molhado $$P_1$$ de ABCD (DG não representa contato com o revestimento) para então obter o raio hidráulico $$R_{h_1}$$ e calcular a vazão $$Q_1,$$ pela fórmula de Manning, $$Q_1=\frac{1}{n}A_1\ R_{h_1}^{2/3}I_0^{1/2}.$$

Subárea A2

Poderíamos realizar o mesmo procedimento anterior, ou calcular a vazão $$Q_2$$ pelos gráficos vistos no Módulo 1 (Figura 10 e Figura 11), considerando que DEF é a metade de um canal trapezoidal e, então, dividir a vazão obtida por 2.

A vazão total da seção composta seria $$Q_T=Q_1+Q_2.$$

Vamos ver um exemplo.

Exemplo 13

Determine a capacidade de vazão do canal cuja seção é mostrada na Figura 9.2. Os taludes e as bermas são de alvenaria de pedra aparelhada em condições regulares $$(n = 0,015),$$ e o fundo de concreto em boas condições $$(n = 0,014).$$ Declividade de fundo $I_{o} =1m/ km$ .

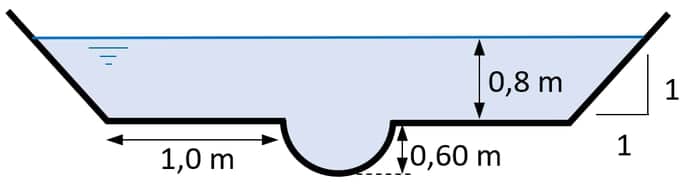
Hidráulica Básica. Porto, 2004, pág. 279. Adaptado por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Dividindo a seção em duas partes, I e II, por linhas verticais, tem-se:

Parte I, seção trapezoidal, revestimento $$n=0,015.$$
Parte II, seção composta, revestimento $$n=0,014.$$

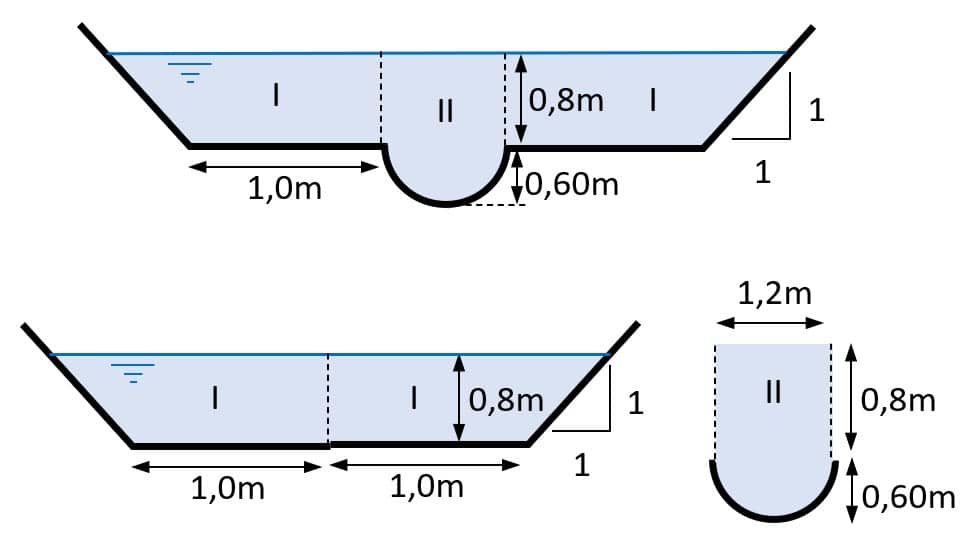
adaptado por: Gabriel de Carvalho Nascimento e Elson Antonio do Nascimento.

Parte I (união dos trapézios laterais), trapezoidal com $$b=2\cdot1,0=2,0m;$$ $$Z=1$$ e $$y = 0,8m:$$

$A = (b + Z y) y = (2 + 1 \cdot 0,8) \cdot 0,8 = 2,24 m$

$P = b + 2 y \sqrt{1 + Z^{2}} = 2 + 2 \cdot 0,8 \cdot \sqrt{1 + 1^{2}} = 4,26 m$

$R_{h} = \frac{A}{P} = \frac{2,24}{4,26} = 0,52 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela fórmula de Manning 7:

$Q_{I} = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2} = \frac{2,24}{0,015} {(0,526)}^{\frac{2}{3}} {(0,001)}^{0,5} = 3,1 m^{3} / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Parte II, fundo circular:

$A = 0,80 \cdot 1,20 + \frac{π \cdot {0,60}^{2}}{2} = 1,52 m^{2}$

$P = π \cdot 0,60 = 1,88 m$

$R_{h} = \frac{A}{P} = 0,81 m$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Pela fórmula de Manning:

$Q_{I I} = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2} = \frac{1,52}{0,014} {(0,81)}^{\frac{2}{3}} {(0,001)}^{0,5} = 3,0 m^{3} / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

A capacidade de vazão da seção total é igual a:

$Q_{t o t a l} = Q_{I} + Q_{I I} ≅ 6 m^{3} / s$

Atenção! Para visualização completa da equação utilize a rolagem horizontal

Mão na Massa

Teoria na prática

Um canal deve ser projetado para atender à demanda de água fluvial (seca) e pluvial (chuva intensa), adotando-se uma seção mista com semicírculo revestido de concreto no centro e trapézios laterais em alvenaria de pedra argamassada, ambos em condições regulares. O solo do local é saibro, o que deve definir a inclinação do talude. Por questões geotécnicas, a profundidade de escavação fica limitada a 2,0m e deve haver uma folga de 20% para a altura máxima d’água.

A vazão de projeto máxima (pluvial) corresponde à drenagem de uma área de 576 mil m² em precipitação de 100mm/h. A vazão mínima (fluvial) corresponde a 1% da máxima, quando o semicírculo da seção central estará totalmente cheio.

Com base nessas premissas, dimensione a seção do canal para declividade de 5,0m/km.

Clique no botão para ver a resolução. Objeto com interação.

RESOLUÇÃO

Dimensionamento e projeto de canais

Verificando o aprendizado

ATENÇÃO!

Para desbloquear o próximo módulo, é necessário que você responda corretamente a uma das seguintes questões:

O conteúdo ainda não acabou.

Clique aqui e retorne para saber como desbloquear.

Conclusão

Considerações Finais

Nos primeiros módulos deste conteúdo, abordamos conhecimentos básicos para cálculo do escoamento em canais em regime permanente e uniforme. Essa condição constitui a maior parte dos cálculos feitos para o dimensionamento de condutos livres para fins diversos, como drenagem e coleta de esgoto.

A análise da energia permite chegar a conclusões importantes para a previsão do comportamento do escoamento, incluindo o estudo do ressalto hidráulico, muito utilizado na jusante de vertedores, para dissipação de energia.

No módulo 3, apresentamos as noções sobre escoamento variado, fornecendo informações para prever o comportamento do nível d’água em diversas condições.

Por fim, ressaltamos aspectos relevantes para o projeto de canais, com uma visão mais abrangente de todas as etapas e os parâmetros envolvidos.

Podcast

Agora veremos um resumo sobre o conteúdo abordado.

CONQUISTAS

Você atingiu os seguintes objetivos:

Lorem ipsum dolor sit amet, consectetur adipiscing elit

Ut enim ad minim veniam, quis nostrud exercitation ullamco

Duis aute irure dolor in reprehenderit in voluptate velit esse

Referências

AZEVEDO NETTO, J. M.; FERNANDEZ Y FERNANDEZ, M.; ARAÚJO, R.; ITO, Acácio Eiji. Manual de Hidráulica. São Paulo: Edgard Blucher, 1998.

BAPTISTA, M. B.; COELHO, M. M. L.; CIRILO, J. A.; MASCARENHAS, F. C. B. (Organizadores). Hidráulica aplicada. 2. ed. Revista e ampliada. Porto Alegre: ABRH, 2003.

CHADWICK, A. Hidráulica para Engenharia Civil e Ambiental. 5. ed. Rio de Janeiro: Elsevier, 2017.

COUTO, L. M. M. Elementos da hidráulica: com EPANET e HEC-RAS. Rio de Janeiro: GEN LTC, 2018.

HOUGHTALEN, R. J. Engenharia Hidráulica. 4. ed. Londres: Pearson, 2012.

PORTO, R. M. Hidráulica básica. São Paulo: EESC-USP, 2004.

PORTO, R. M. Hidráulica básica. 5. ed. São Carlos: EESC-USP, 2006.

Explore+

Para saber mais sobre os assuntos tratados neste tema, leia:

Coeficiente de rugosidade de Manning para o rio Paracatu, de Lyra et al.
Modelagem hidrodinâmica tridimensional em canais utilizando o modelo de turbulência k-e, de Francisco Assis Souza Filho, Erika da Justa Teixeira Rocha, Ernesto Pitombeira e Iran E. Lima Neto.
Cálculo do escoamento uniforme em canais retangulares lisos a partir da formulação universal de perdas de carga: aplicação a dados experimentais, de Tarciso Cabral da Silva e Márcia Suzanna Dutra de Abreu.
Brasil em desenvolvimento: Estado, planejamento e políticas públicas, do Instituto de Pesquisa Econômica Aplicada (IPEA).
Aspectos operacionais da transposição do rio São Francisco, de Ana Beatriz Gomes Vanderlei.
Otimização de custos de adução na transposição do rio São Francisco, de Francisco Jacomé Sarmento.

Conteudista

Gabriel de Carvalho Nascimento

Currículo Lattes

Descrição

PROPÓSITO

Preparação

OBJETIVOS

Módulo 1

Módulo 2

Módulo 3

Módulo 4

Escoamento em condutos livres

MÓDULO 1

Introdução

Cálculo em regime permanente e uniforme

Classificações de canais livres

Conduto forçado

Conduto livre

Naturais

Artificiais

Saiba mais

Prismáticos

Não prismáticos

Principais parâmetros

Geral

Re=ρVDhμ

Dh=4Rh

Fr=VgHm

Seções trapezoidais

A=(b+Zy)y

B=b+2Zy

P=b+2y1+Z2

Rh=AP=b+Zyyb+2y1+Z2

Seções circulares

A=D2θ-senθ8

B=Dsenθ2

P=θD2

Rh=AP=D(θ-senθ)4θ

θ=2arccos1-2yD

Exemplo 1

Taludes

Cálculo do escoamento permanente e uniforme

Equação da tensão cisalhante

Cisalhante

∑Fx=F1+W⏞γ∀=γAL·senα-F2-τ0·Ar ⏞PL=0

τ0PL=γALsen⁡α

τ0=γAI0P=γ⏞ρgRhI0

Exemplo 2

Equação de Manning

V=8gf⏞CRhI0

V=1nRh2/3I01/2

Q=An Rh2/3 I01/2

Exemplo 3

Saiba mais

Cálculo da altura

nQI0=A Rh2/3

Seção retangular muito larga (b >> y)

A=by

P=b+2y

Rh=AP=byb+2y

Rh≅byb=y

nQI0=by y2/3

y=nQbI03/5

Seção trapezoidal (incluindo retangular e triangular)

KTy=nQb8/3 Io=yb5/31+ybZ5/31+2yb1+Z²2/3

Exemplo 4

KTb=nQIo3/8=y0m+Z5m+21+Z²21/8

Canais circulares

KC=1DnQI03/8=θ-sen⁡θ5213 θ21/8

y0D=121-cos⁡θ2

Exemplo 5

Eficiência hidráulica de seções

m=by

A=m+Zy2→ y=A1/2m+Z1/2

P=m+21+Z2y

A=m+Zy2→ y=A1/2m+Z1/2 P=m+21+Z2y → P=m+21+Z2A1/2m+Z1/2

dPdm=0

m=by=21+Z²-Z

M=nQI03/8

Km=m+Z5m+21+Z221/8

y=MKm

Exemplo 6

Mão na Massa

$R e = \frac{ρ V D_{h}}{μ}$

$D_{h} = 4 R_{h}$

$F r = \frac{V}{\sqrt{g H_{m}}}$

$A = (b + Z y) y$

$B = b + 2 Z y$

$P = b + 2 y \sqrt{1 + Z^{2}}$

$R_{h} = \frac{A}{P} = \frac{(b + Z y) y}{b + 2 y \sqrt{1 + Z^{2}}}$

$A = D^{2} \frac{(θ - s e n θ)}{8}$

$B = D s e n (\frac{θ}{2})$

$P = \frac{θ D}{2}$

$R_{h} = \frac{A}{P} = D \frac{(θ - s e n θ)}{4 θ}$

$θ = 2 \arccos (1 - 2 \frac{y}{D})$

$\sum F_{x} = F_{1} + \overset{γ \forall = γ A L}{\overset{⏞}{W}} \cdot s e n α - F_{2} - τ_{0} \cdot \overset{P L}{\overset{⏞}{A_{r}}} = 0$

$τ_{0} P L = γ A L sen α$

$τ_{0} = \frac{γ A I_{0}}{P} = \overset{ρ g}{\overset{⏞}{γ}} R_{h} I_{0}$

$V = \overset{C}{\overset{⏞}{\sqrt{\frac{8 g}{f}}}} \sqrt{R_{h} I_{0}}$

$V = \frac{1}{n} R_{h}^{2 / 3} I_{0}^{1 / 2}$

$Q = \frac{A}{n} R_{h}^{2 / 3} I_{0}^{1 / 2}$

$\frac{n Q}{\sqrt{I_{0}}} = A R_{h}^{2 / 3}$

$A = b y$

$P = b + 2 y$

$R_{h} = \frac{A}{P} = \frac{b y}{b + 2 y}$

$R_{h} ≅ \frac{b y}{b} = y$

$\frac{n Q}{\sqrt{I_{0}}} = (b y) y^{2 / 3}$

$y = {(\frac{n Q}{b \sqrt{I_{0}}})}^{3 / 5}$

$K_{T y} = \frac{n Q}{b^{8 / 3} \sqrt{I_{o}}} = {(\frac{y}{b})}^{5 / 3} \frac{{[1 + (\frac{y}{b}) Z]}^{5 / 3}}{{[1 + 2 (\frac{y}{b}) \sqrt{1 + Z ²}]}^{2 / 3}}$

$K_{T b} = {(\frac{n Q}{\sqrt{I_{o}}})}^{3 / 8} = y_{0} {[\frac{{(m + Z)}^{5}}{{(m + 2 \sqrt{1 + Z ²})}^{2}}]}^{1 / 8}$

$K_{C} = \frac{1}{D} {(\frac{n Q}{\sqrt{I_{0}}})}^{3 / 8} = {[\frac{{(θ - s e n θ)}^{5}}{2^{13} θ^{2}}]}^{1 / 8}$

$\frac{y_{0}}{D} = \frac{1}{2} (1 - \cos \frac{θ}{2})$

$m = \frac{b}{y}$

$A = (m + Z) y^{2} \to y = \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}}$

$P = (m + 2 \sqrt{1 + Z^{2}}) y$

$\begin{matrix} A = (m + Z) y^{2} \to y = \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}} \\ P = (m + 2 \sqrt{1 + Z^{2}}) y \end{matrix}\} \to P = (m + 2 \sqrt{1 + Z^{2}}) \frac{A^{1 / 2}}{{(m + Z)}^{1 / 2}}$

$\frac{d P}{d m} = 0$

$m = \frac{b}{y} = 2 (\sqrt{1 + Z ²} - Z)$

$M = {(\frac{n Q}{\sqrt{I_{0}}})}^{3 / 8}$

$K_{m} = {[\frac{{(m + Z)}^{5}}{{(m + 2 \sqrt{1 + Z^{2}})}^{2}}]}^{1 / 8}$

$y = \frac{M}{K_{m}}$

$H_{i} = z_{i} + \frac{p_{i}}{γ} + α \frac{V_{i}^{2}}{2 g}$

$H_{i} = z_{i} + y_{i} + \frac{V_{i}^{2}}{2 g}$

$E_{i} = y_{i} + \frac{V^{2}}{2 g}$

$E_{i} = y_{i} + \frac{Q^{2}}{2 g A^{2}}$

$E = y + \frac{q^{2}}{2 g y^{2}}$

$y_{c} = {(\frac{q^{2}}{g})}^{\frac{1}{3}}$

$E_{c} = \frac{3}{2} y_{c}$

$q_{m a x} = \sqrt{\frac{8 g}{27}} \sqrt{E_{0}}$

$\frac{d E}{d y} = 0 \to 1 - 2 \frac{Q^{2}}{2 g A^{3}} \frac{d A}{d y} = 0 \to \frac{Q^{2}}{g A^{3}} \frac{d A}{d y} = 1$

$\frac{Q^{2}}{g A^{3}} B = 1$

$\to \frac{{(Q / A)}^{2}}{g A} B = 1 \to \frac{V^{2}}{g \frac{A}{B}} = 1$

$\to \frac{V^{2}}{g H_{m}} = 1 \to \frac{V}{\sqrt{g H_{m}}} = 1$

$F r = \frac{V}{\sqrt{g H_{m}}}$

$I_{c} = n^{2} g y_{c} {(\frac{2 y_{c} + b}{y_{c} b})}^{4 / 3}$

$\frac{y_{2}}{y_{1}} = \frac{1}{2} [\sqrt{1 + 8 F r_{1}^{2}} - 1]$

$\frac{y_{1}}{y_{2}} = \frac{1}{2} [\sqrt{1 + 8 F r_{2}^{2}} - 1]$

$∆ E = \frac{{(y_{2} - y_{1})}^{3}}{4 y_{2} y_{1}}$

$η = \frac{∆ E}{E_{1}}$

$y_{c} = {(\frac{q^{2}}{g})}^{\frac{1}{3}}$

$I_{c} = n^{2} g y_{c} {(\frac{2 y_{c} + b}{y_{c} b})}^{4 / 3}$

$I_{0} > I_{c}$ e $y_{n} < y_{c}$ : declividade forte − S (steep slope).

$0 < I_{0} < I_{c}$ e $y_{n} > y_{c}$ : declividade fraca − M (mild slope).

$I_{0} < 0$ : aclive – A (adverse slope).

$E = y_{f} - y_{0} \to \frac{d E}{d x} = \overset{- I_{f}}{\overset{⏞}{\frac{d y_{f}}{d x}}} - \overset{- I_{0}}{\overset{⏞}{\frac{d y_{0}}{d x}}}$

$\to d x = \frac{d E}{I_{0} - I_{f}}$

$Δ x = \frac{E_{2} - E_{1}}{I_{0} - {\bar{I}}_{f}}$

$I_{f} = n^{2} q^{2} {(\frac{b + 2 y}{y^{5 / 2} b})}^{4 / 3}$

$c = \sqrt{\frac{g y_{2}}{2 y_{1}} (y_{1} + y_{2})}$

$V_{ω} = V_{1} \pm c$