Objetivos
Elementos geométricos planimétricos
Calcular os elementos geométricos planimétricos.
Superelevação e superlargura de uma rodovia
Calcular superelevação e superlargura de uma rodovia.
Elementos geométricos altimétricos
Calcular os elementos geométricos altimétricos.
Seções transversais no projeto geométrico de rodovias
Reconhecer as seções transversais mais comuns no projeto geométrico de rodovias.
Processo de projeto de rodovias
Em nosso material, unidades de medida e números são escritos juntos (ex.: 25km) por questões de tecnologia e didáticas. No entanto, o Inmetro estabelece que deve existir um espaço entre o número e a unidade (ex.: 25 km). Logo, os relatórios técnicos e demais materiais escritos por você devem seguir o padrão internacional de separação dos números e das unidades.
O eixo de uma estrada é seu alinhamento longitudinal, e sobre ele inicia-se um traçado rodoviário. Nas estradas de rodagem, o eixo localiza-se na região central da pista de rolamento. A apresentação de um projeto em planta consiste na disposição de uma série de segmentos retos, concordados pelas curvas horizontais.
Tais concordâncias podem ocorrer diretamente, com um arco de círculo ou pela inserção de um arco de espiral entre as tangentes e os arcos de círculo. Vamos conhecer, então, os elementos relacionados ao alinhamento longitudinal:
Alinhamentos retos
São os trechos retos situados entre duas curvas de concordância; por serem tangentes a essas mesmas curvas, são denominados simplesmente tangentes. Os alinhamentos retos restantes são chamados de tangentes externas.
Elementos geométricos axiais.
Em que:
- $$$\beta_{1}$$$, $$$\beta_{2}$$$, $$$\beta_{3}$$$ = São os azimutes dos alinhamentos.
- $$$AZIMUTE$$$ = É o ângulo que a direção faz com o norte magnético, medido no sentido horário.
- $$$\theta_{1}$$$, $$$\theta_{2}$$$ = São os ângulos de deflexão.
- $$$AB$$$, $$$DE$$$, $$$GH$$$ = São as tangentes.
- $$$BC$$$, $$$CD$$$, $$$EF$$$, $$$FG$$$ = São as tangentes externas.
- $$$BD$$$, $$$EG$$$ = Desenvolvimento das curvas de concordância.
Curvas horizontais
As curvas de concordância horizontal são os elementos utilizados para concordar os alinhamentos retos. Essas curvas podem ser classificadas em:
Determinadas por um arco de circunferência, como mostrado na figura a seguir. Existem pontos particulares de importância na concordância entre os trechos retos e o arco de circunferência. O ponto que passa da tangente para o arco de círculo é o ponto de curva, ou PC, e o ponto que passa da curva para a tangente seguinte é chamado de ponto de tangência, ou PT.
Curva circular simples
Quando se utilizam dois ou mais arcos de curvas circulares de raios diferentes, para concordar os alinhamentos retos.
Curva circular compostas sem transição.
Quando se empregam as espirais de transição na concordância dos alinhamentos retos.
Curva circular compostas sem transição.
Quando duas curvas se cruzam em sentidos opostos com o ponto de tangência em comum.
Curva circular reversa.
Estaqueamento
Ante a necessidade de se identificar elementos do traçado como pontos notáveis e curvas, estabeleceu-se um sistema de demarcação de pontos igualmente distanciados. Estes são chamados de estacas e distam 20m entre si.
O sistema mais utilizado para nomeá-las é a numeração sequencial das estacas, de 20 em 20m, a partir de um ponto inicial chamado de estaca 0.
Pontos notáveis situados no intervalo das estacas são identificados pela distância medida a partir da estaca menor e denominados estacas fracionárias ou intermediárias.
Para concordar dois alinhamentos retos, é mais utilizada a curva circular simples, devido à simplicidade para ser projetada e locada.
Curva horizontal circular simples.
Em que:
- PC = ponto de curva ou ponto de curvatura;
- PT = ponto de tangente ou ponto de tangência;
- PI = ponto de interseção das tangentes;
- D = desenvolvimento da curva;
- Δ = ângulo de deflexão;
- AC = ângulo central da curva;
- R = raio da curva circular;
- T = tangente externa;
- O = centro da curva;
- E = afastamento;
- G = grau da curva;
- c = corda;
- d = deflexão sobre a tangente.
Veja o detalhamento de alguns desses componentes a seguir:
São os segmentos de retas que vão do PC ao PI ou do PI ao PT. Pode-se determinar o comprimento "T" relacionando o ângulo central e o raio, dentro do triângulo PC, O, PI, obtendo-se:
$$$ T=R \cdot \operatorname{tg}\left(\frac{A C}{2}\right) $$$
É o comprimento do arco do círculo que vai desde o PC ao PT. Obtido pela regra de três entre o comprimento do desenvolvimento e o comprimento total da circunferência, conforme mostrado a seguir:
$$$ D=\frac{\pi \cdot R \cdot A C}{180^{0}} $$$
Chama-se "grau da curva circular" o ângulo central que compreende uma corda de um dado comprimento (c). O grau é independente do ângulo central.
$$$ G=2 \cdot \operatorname{arcsen}\left(\frac{c}{2 \cdot R}\right) $$$
É a distância entre o PI e a curva. Considerando o triângulo O, PC, PI, tem-se:
$$$ E=T \cdot \operatorname{tg}\left(\frac{A \cdot C}{4}\right) $$$
Para prosseguir, é necessário entender a diferença entre raio da curva e ângulo central:
Raio da curva (R)
É o raio do arco do círculo empregado na concordância, normalmente expresso em metros. É um elemento selecionado por ocasião do projeto, de acordo com as características técnicas da rodovia e a topografia da região.
Ângulo central (AC)
É o ângulo formado pelos raios que passam pelo PC e PT e que se interceptam no ponto O. Tais raios são perpendiculares nos pontos de tangência PC e PT. Este ângulo é numericamente igual a deflexão $$$(\Delta)$$$ entre os dois alinhamentos.
Roteiro de cálculo
Conhecendo-se o raio da curva (R) e o ângulo central (AC), o roteiro para o cálculo dos demais elementos da curva circular simples é o seguinte:
Determinação do valor da tangente "T".
Deduzindo o valor da tangente "T" da estaca do "PI", tem-se a estaca do "PC" ("PCD" se for curva à direita e "PCE" se for curva à esquerda).
Cálculo do Desenvolvimento "D", que é a extensão do trecho em curva.
Determinação da estaca do "PT" somando-se ao valor da estaca do "PC", o valor do Desenvolvimento "D".
São quatro as curvas que podem ser auxiliares como transição:
- A clotóide (também denominada espiral de cornu, radióide aos arcos ou espiral de Van Leber);
- A lemniscata de Bernouille;
- A curva elástica (também denominada de radióide às abscissas);
- A parábola cúbica.
Comentário
Neste estudo, vamos falar mais sobre a clotóide, que é a curva de transição especificada pelos órgãos viários brasileiros.
Por definição, a clotóide, ou espiral, é uma curva tal que os raios de curvatura em qualquer de seus pontos são inversamente proporcionais aos desenvolvimentos de seus respectivos arcos.
Curva circular com transição.
Os elementos principais da transição são:
- $$$TS$$$ ou $$$TE$$$ = ponto Tangente-Espiral: ponto de passagem do alinhamento reto para a curva espiral;
- $$$SC$$$ ou $$$EC$$$ = ponto Espiral-Curva Circular: ponto de passagem da curva circular para a curva espiral;
- $$$CS$$$ ou $$$CE$$$ = ponto Curva Circular-Espiral: ponto de passagem da curva circular para a curva espiral;
- $$$ST$$$ ou $$$ET$$$ = ponto Espiral-Tangente: ponto de passagem da curva espiral para o alinhamento reto;
- $$$PC'$$$ e $$$PT'$$$ = recuos de PC e PT originais devido à introdução da espiral;
- $$$P$$$ e $$$P'$$$ = pontos de passagem da espiral;
- $$$Rc$$$ = Raio da Curva Circular;
- $$$\Delta$$$ = ângulo central ou deflexão das tangentes $$$=\theta+2 \cdot S c$$$;
- $$$Sc$$$ = ângulo central da transição: angulo central do trecho em espiral. Este ângulo pode ser calculado pelas expressões:
$$$ \begin{aligned} &S_{c}=\frac{l_{e}}{2 \cdot R_{c}}(\text{ em radianos}) \\\\ &S_{c}=\frac{l_{e} \cdot 180^{0}}{2 \pi \cdot R_{c}}(\text{ em graus}) \end{aligned} $$$
- $$$\boldsymbol{D}_{\boldsymbol{\theta}}$$$ = Desenvolvimento do trecho circular, após a intercalação da espiral. Se for igual a zero, marca o comprimento máximo de transição na curva, em uma situação em que espirais se encontram:
$$$ D_{\theta}=\frac{\pi \cdot R_{c} \cdot \theta}{180^{0}} $$$
- $$$Le$$$ = comprimento da curva de transição: para fins práticos, o menor comprimento de transição admissível é de 30m ou equivalente à distância percorrida por um veículo, na velocidade diretriz, no tempo de 2 segundos, prevalecendo o maior. Por outro lado, o comprimento máximo de transição ocorre quando as espirais se encontram e o ângulo central da curva circular é zero.
$$$ \begin{gathered} L e_{\min} \geq 30 m \\\\ L e_{\min}=0,556 \mathrm{~V} \\\\ L e_{\operatorname{má} x}=\frac{R \cdot A C^{\mathrm{o}} . \pi}{180^{\mathrm{o}}} \end{gathered} $$$
Atenção
Uma fórmula muito utilizada para o comprimento mínimo de transição é o critério dinâmico de Barnett, que aponta a seguinte fórmula a partir do raio da curva circular em metros e da velocidade diretriz da rodovia em km/h:
$$L e_{\min }=0,036 \frac{V^{3}}{R c}$$
Em um traçado com duas curvas circulares horizontais, em que AC1 (primeiro ângulo central) é de 40° e AC2 (segundo ângulo central) é de 28°. Se a distância entre os dois pontos de inflexão é de 720m, calcule o maior raio possível para as duas curvas, sabendo que os dois raios são iguais.
A equação da tangente é a representada a seguir, em que a tangente é diretamente proporcional ao raio e ao ângulo central.
$$$ T=R \cdot \operatorname{tg}\left(\frac{A C}{2}\right) $$$
Para conseguirmos o maior raio possível, devemos usar a maior tangente dentro do espaço disponível. Ou seja, o ponto de tangente da primeira curva deve coincidir com o ponto de curvatura da segunda curva. Assim, tem-se que T1 + T2 = 720, que é a distância entre os dois pontos de inflexão. Devemos aplicar a equação da tangente às duas curvas, como a seguir:
$$$ \begin{gathered} R \cdot \operatorname{tg}\left(\frac{40}{2}\right)+R \cdot \operatorname{tg}\left(\frac{28}{2}\right)=720 \\\\ R \cdot \operatorname{tg}(20)+R \cdot \operatorname{tg}(14)=720 \\\\ R \cdot(\operatorname{tg}(20)+\operatorname{tg}(14))=720 \\\\ \mathrm{R}=1173,98 \mathrm{~m} \end{gathered} $$$
Cálculo de uma curva circular
Quando se define a velocidade diretriz para o projeto geométrico de uma estrada, busca-se estabelecer condições tais que permitam aos usuários o desenvolvimento e a manutenção de velocidades de percurso próximas a essa velocidade de referência em condições de conforto e segurança.
Essas condições de operação naturalmente, devem ser analisadas em duas situações diferentes.

Trecho em tangente
Quando percorre um trecho em tangente, um motorista experimenta alguma facilidade para efetuar pequenas manobras de ajuste lateral durante o curso do automóvel, não estando sujeito a esforços laterais devido à geometria da rodovia.

Trecho em curva
Quando percorre um trecho em curva, estes esforços laterais surgem e passam a atuar sobre o veículo. De forma geral, há uma sensação de maior confinamento imposta pelo trecho em curva a um usuário, influenciando sua disposição em manter a velocidade de operação nos trechos em tangente e em curva.
Assim, surgem os conceitos de superelevação e superlargura para minimizar o impacto negativo desses fatores inerentes aos trechos curvos, que trazem condições de operação mais homogêneas para os usuários ao longo das estradas. Vamos estudá-los, portanto!
Ao percorrer um trecho de rodovia em curva horizontal com certa velocidade, um veículo fica sujeito à ação de uma força centrífuga, que atua no sentido de dentro para fora da curva, tendendo a mantê-lo em trajetória retilínea, tangente à curva, como é mostrado na figura a seguir. Isso obriga o condutor do veículo a virar o volante no sentido da curva para manter o veículo na trajetória desejada.
Forças atuantes num veículo em curva.
Em que:
- P = peso do veículo;
- N = reação normal à superfície do pavimento, devido ao peso do veículo;
- Fa = força de atrito transversal;
- Fc = força centrífuga;
A superelevação é medida pela inclinação transversal da pista em relação ao plano horizontal, sendo expressa em proporção (m/m) ou em percentagem (%). Estando a pista inclinada com um ângulo α, a superelevação (e) pode ser expressa por:
$$$ e=\operatorname{tg} \alpha \text{ (proporção em m/m)} $$$
$$$ou$$$
$$$ e=100 \cdot \operatorname{tg} \alpha(\%) $$$
Com as leis de equilíbrio no eixo x e y, e relacionando as duas expressões, temos gerada a seguinte equação:
$$$ \frac{v^{2}}{g \cdot R} \cdot(1-f \cdot e)=e+f $$$
Em que:
- m = massa do veículo, em kg;
- v = velocidade diretriz, em m/s;
- R = raio de curvatura horizontal, em m;
- f = coeficiente de atrito transversal pneu/pavimento;
- g = aceleração da gravidade, em m/s².
Nos casos normais de rodovias rurais, o coeficiente de atrito (f) e o valor da superelevação (e) são pequenos, de modo que o produto (f. e) aproxima-se de zero. Assim, temos:
$$$ \frac{v^{2}}{g \cdot R}=e+f \quad \rightarrow \quad e=\frac{v^{2}}{g \cdot R}-f $$$
Nas unidades usuais, ou seja, R em metros, V em km/h e g = 9,8m/s², tem-se:
$$$ e=\frac{V^{2}}{127 \cdot R}-f $$$
Onde:
- e = superelevação (m/m);
- V = velocidade diretriz (km/h);
- R = raio de curvatura (m);
- f = coeficiente de atrito transversal, entre pneu/pavimento.
A relação entre f e a velocidade é dada por meio da tabela a seguir:
| $$V (km/h)$$ | $$ f_{\text{máx}} $$ |
|---|---|
| 30 | 0,2 |
| 40 | 0,18 |
| 50 | 0,16 |
| 60 | 0,15 |
| 70 | 0,15 |
| 80 | 0,14 |
| 90 | 0,14 |
| 100 | 0,13 |
| 110 | 0,12 |
| 120 | 0,11 |
Tabela: Relação entre coeficiente de atrito
transversal pneu/pavimento e velocidade.
Extraído de Manual de projeto
geométrico de rodovias rurais (DNER, 1999, p.71)
Para curvas com raios muito grandes em relação à velocidade diretriz de projeto, os efeitos da força centrífuga resultariam desprezíveis, sendo possível projetar seções transversais da pista nessas curvas nas mesmas condições consideradas para os trechos em tangente, ou seja, com abaulamentos, dispensando o uso de superelevações.
A relação ente velocidade e raio é dada por meio da tabela a seguir:
| $$V (km/h)$$ | $$ R (m) $$ |
|---|---|
| 30 | 450 |
| 40 | 800 |
| 50 | 1250 |
| 60 | 1800 |
| 70 | 2450 |
| 80 | 3200 |
| 90 | 4050 |
| >100 | 5000 |
Tabela: Relação entre velocidade diretriz e raio de
curvatura.
Extraído de Manual de projeto geométrico de rodovias rurais (DNER,
1999, p.97)
Por outro lado, pode-se relacionar as taxas de superelevação máxima em 8 ou 10%, sendo 10% reservado para as Classes 0 e I, e 8% reservado para as outras Classes.
Em regra geral, o critério para a determinação dos valores de superelevação para qualquer curva horizontal é a adotada pela seguinte equação:
$$$ e_{R}=e_{m á x}\left(\frac{2 \cdot R_{\min} n}{R}-\frac{R_{\min}^{2}}{R^{2}}\right) $$$
Onde:
- $$$\mathrm{e}_{\mathrm{R}}=$$$ superelevação a adotar para a curva com raio $$$\mathrm{R}$$$, em $$$\%$$$;
- $$$\mathrm{e}_{\mathrm{máx}}=$$$ superelevação máxima para a classe de projeto, em $$$\%$$$;
- $$$\mathrm{R}_{\min }=$$$ raio mínimo de curva para a velocidade diretriz dada, em $$$\mathrm{m}$$$;
- $$$\mathrm{R}=$$$ raio da curva circular utilizada na concordância, em $$$\mathrm{m}$$$.
As normas, manuais ou recomendações de projeto geométrico estabelecem as larguras mínimas de faixas de trânsito a adotar para as diferentes classes de projeto, levando em consideração aspectos de ordem prática, tais como as larguras máximas dos veículos de projeto e as respectivas velocidades diretrizes para o projeto.
Essas faixas de trânsito são fixadas com folgas suficientes em relação à largura máxima dos veículos, para permitir tanto sua acomodação estática, mas também suas variações de posicionamento em relação às trajetórias longitudinais.
O cálculo é feito baseado na fórmula a seguir:
$$$ \mathrm{L}=2 \cdot l+f $$$
Onde:
- $$$l$$$ = a largura do veículo padrão considerado;
- $$$f$$$ = a folga.
Curiosidade
Nos trechos em curva os veículos ocupam fisicamente espaços laterais maiores do que as suas próprias larguras.
Devido a efeitos de deformação visual às dificuldades naturais de um veículo pesado em trajetória curva, os trechos em curva horizontal provocam aparência de estreitamento da pista à frente dos usuários, provocando sensação de confinamento.
Para compensar esses fatores, os trechos em curva podem ser alargados, de forma a oferecer aos usuários melhores condições de continuidade quanto à sensação de liberdade de manobra ou melhores condições de fluidez, no que diz respeito à disponibilidade de largura de faixa de trânsito.
Denomina-se superlargura à largura adicional das faixas de trânsito, a ser projetada para os trechos em curva sendo representada pela letra S.
O método do DNER assevera que a superlargura é obtida calculando a largura total da pista necessária no trecho curvo, para o veículo de projeto adotado, deduzindo a largura básica estabelecida para a pista em tangente.
Trajetória de um veículo numa curva.
A fórmula da superlargura é dada por:
$$$ \mathrm{S}=\mathrm{Lt}-\mathrm{Lb} $$$
Em que:
$$$ L t=2(\mathrm{Gc}+\mathrm{Gl}+\mathrm{Gbd})+\frac{V}{10 \sqrt{R}} $$$
Sendo:
- S = superlargura total (m);
- R = raio da curva(m);
- Lt = largura total da pista de rolamento com duas faixas, na curva (m);
- Lb = largura da pista de rolamento com duas faixas, em tangente (m);
- Gl = folga lateral do veículo de projeto em movimento (m).
| $$Lb (m)$$ | $$Gl (m)$$ |
|---|---|
| 6,00/6,40 | 0,60 |
| 6,60/6,80 | 0,75 |
| 7,00/7,20 | 0,90 |
Tabela: Relação entre a largura da pista e a folga
lateral do veiculo.
Extraído de Manual de projeto geométrico de rodovias
rurais (DNER, 1999, p.76)
É necessário calcular também o gabarito estático do veículo de projeto (m). O Gc, pode ser calculado de acordo com a fórmula:
$$$ G c=L v+\frac{E^{2}}{2 R} $$$
Onde:
- Lv = a largura física do veículo de projeto, em metros. Para veículos de projeto semirreboques e caminhões, Lv = 2,60m.
- E = a distância entre eixos do veículo de projeto, em metros.
- R é o raio da curva circular.
Já o gabarito de balanço dianteiro GBD de um veículo, em metros, pode ser obtido da seguinte maneira:
$$$ G b d=\sqrt{R^{2}+B d(2 E+B d)}-R $$$
Atenção
Para caminhões, considera-se:
- BD = 1,20m;
- E = 6,10m.
A tabela a seguir apresenta os valores dos raios, acima dos quais é dispensável o alargamento:
| V (km/h) | 30 | 40 | 50 | 60 | 70 | 80 | 90 | >100 | Tipo de veículo |
|---|---|---|---|---|---|---|---|---|---|
| Largura básica da pista em tangente = 7,20 m | |||||||||
| R (m) | 130 | 160 | 190 | 220 | 260 | 310 | 360 | 420 | Caminhão |
| R (m) | 270 | 300 | 340 | 380 | 430 | 480 | 540 | 600 | Semirreboque |
| Largura básica da pista em tangente = 6,60 m | |||||||||
| R (m) | 340 | 430 | 550 | 680 | 840 | 1000 | Caminhão | ||
Tabela: Valores dos raios nos quais é dispensável o
alargamento.
Extraída de Manual de projeto geométrico de rodovias rurais
(DNER, 1999, p.77-79)
Calcule a superlargura em uma curva horizontal, dados os seguintes elementos:
- Largura do veículo: Lv = 2,50m;
- Distância entre os eixos do veículo: 6,50 m (E);
- Distância entre a frente do veículo e o eixo dianteiro: 1,10m (Bd);
- Raio da curva: 280 m;
- Velocidade de projeto: V = 90 km/h;
- Faixas de tráfego de 3,3 m (Lb = 6,6 m);
- Número de faixas: 2.
Vamos calcular, inicialmente, cada parcela da superlargura. Como Lb = 6,6m, Gl, de acordo com a tabela a seguir, é igual a 0,75.
| $$Lb (m)$$ | $$Gl (m)$$ |
|---|---|
| 6,00/6,40 | 0,60 |
| 6,60/6,80 | 0,75 |
| 7,00/7,20 | 0,90 |
Tabela: Relação entre a
largura da pista e a folga lateral do
veiculo.
Extraído de Manual de projeto geométrico
de rodovias rurais (DNER, 1999, p.76)
Agora, o gabarito estático do veículo, de acordo com a fórmula:
$$$ G c=L v+\frac{E^{2}}{2 R} $$$
Substituindo:
$$$ G c=2,5+\frac{6,5^{2}}{2\cdot280}=2,575 \mathrm{~m} $$$
Gbd é o balanço dianteiro do veículo, em metros, de acordo com a fórmula:
$$$ G b d=\sqrt{R^{2}+B d(2 E+B d)}-R $$$
Substituindo:
$$$ \begin{gathered} G b d=\sqrt{280^{2}+1,10(2.6,5+1,10)}-280 \\\\ G b d=0,028 \mathrm{~m} \end{gathered} $$$
Agora que temos todas as parcelas, calculemos a superlargura:
$$$ \begin{gathered} L t=2(2,575+0,75+0,028)+\frac{90}{10 \sqrt{280}} \\\\ L t=7,216 \mathrm{~m} \end{gathered} $$$
Mas:
$$$ \begin{gathered} \mathrm{S}=L t-L b \\\\ S=7,216-6,6=0,62 \mathrm{~m} \end{gathered} $$$
Resposta: A superlargura é de 0,62m. Em condições práticas, arredonda-se para o múltiplo de 0,20 m imediatamente superior.
Cálculo de superlargura de uma curva
O projeto de uma estrada em perfil é constituído de greides retos, concordados dois a dois por curvas verticais. Os greides retos são definidos pela sua declividade, que é a tangente do ângulo que fazem com a horizontal. Na prática, a declividade é expressa em porcentagem.
Perfil de uma estrada.
Em que:
PIV (ponto de interseção vertical)
É a interseção dos greides retos.
PCV (ponto de curvatura vertical)
São os pontos de tangência.
PTV (ponto de tangência vertical)
É o ponto de transição após a curva vertical e a próxima rampa.
A tarefa do projetista é adequar o perfil da futura estrada, de tal forma que os veículos a percorram em uma razoável uniformidade de operação.
Durante essa tarefa de adequação, é importante se atentar aos elementos a seguir:
É a representação, no plano vertical, das diferenças de nível, cotas ou altitudes, obtidas do resultado de um nivelamento feito ao longo do eixo de uma estrada.
São linhas de declividade uniforme que tem como finalidade substituir as irregularidades naturais do terreno, possibilitando o seu uso para fins de projeto. A sua representação, no plano vertical, corresponde a um perfil constituído por um conjunto de retas, concordado por curvas, que, no caso de um projeto rodoviário, corresponderá ao nível atribuído à estrada.
Para fazer a adequação do perfil da estrada, o projetista também precisa considerar as rampas de referências e como cada tipo de veículo passará por elas.

Veículos de passageiros
Conseguem vencer rampas de 4% a 5%, com perda de velocidade muito pequena. Em rampas de até 3%, o comportamento desses veículos é praticamente o mesmo que nos trechos em nível.

Caminhões
Rampas máximas com até 6% afetam bastante o movimento de caminhões, especialmente os pesados, quando superior a 7% só devem ser utilizadas em estradas de baixo volume de tráfego ou destinadas ao tráfego exclusivo de veículos de passeio.
Note que a perda de velocidade dos caminhões em rampas é bem maior que a dos veículos de passageiros.
A tabela a seguir apresenta valores de inclinações máximas correspondendo às classes de projeto e ao relevo da rodovia, recomendadas pelas Normas para Projeto de Estradas de Rodagem do DNER.
| Classe do projeto | Relevo | ||
|---|---|---|---|
| Plana | Ondulada | Montanhosa | |
| Classe 0 | 3 | 4 | 5 |
| Classe I | 3 | 4,5 | 6 |
| Classe II | 3 | 5 | 6 |
| Classe III | 3 | 5 a 6 | 6 a 7 |
| Classe IV | 3 | 5 a 7 | 6 a 9 |
Tabela: Valores de inclinações máximas de acordo com
as classes de projeto e ao relevo da rodovia
Elaborada por Giuseppe Miceli
Junior
Atenção
Para evitar problemas no escoamento no sentido longitudinal, é aconselhável o uso de rampas com inclinação não inferior a 0,5% em estradas.
Diferença Algébrica de Rampas ou Grau da curva (g)
É numericamente igual à diferença algébrica das declividades dos greides retos a concordar, ou seja:
$$$ g=i 1-i 2 $$$
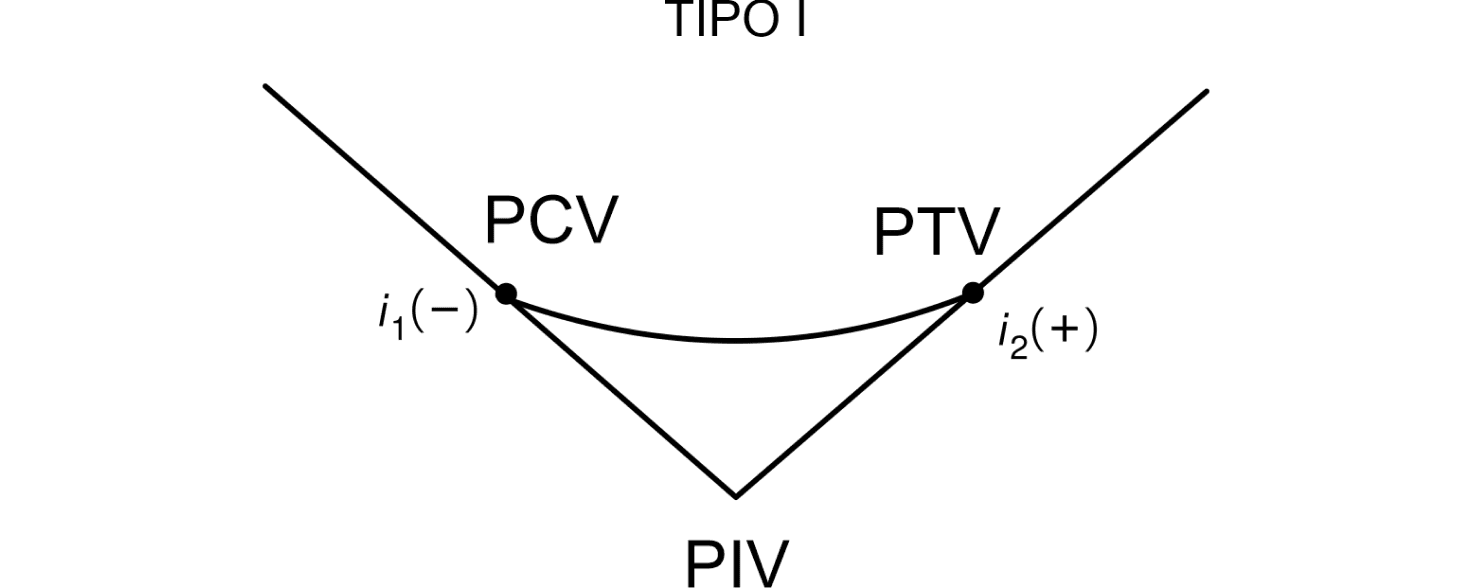
O valor do grau da curva (g) influencia no tipo da curva, veja:
Curva convexa
Quando $$$g>0$$$ significa que a curva vertical parabólica é convexa.
Curva côncava
Quando $$$g<0$$$ significa que a curva vertical parabólica é côncava.
A seguir, você pode ver exemplos de curvas côncavas e convexas.
Curvas convexas
Exemplos de curvas convexas são:
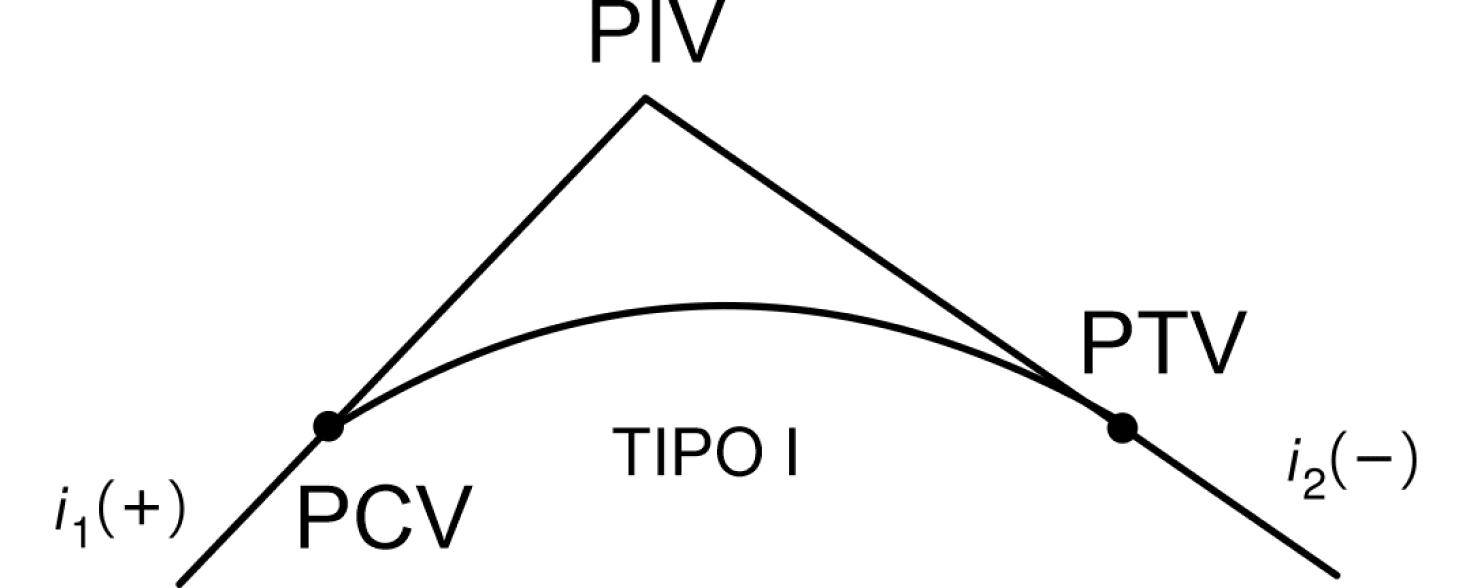
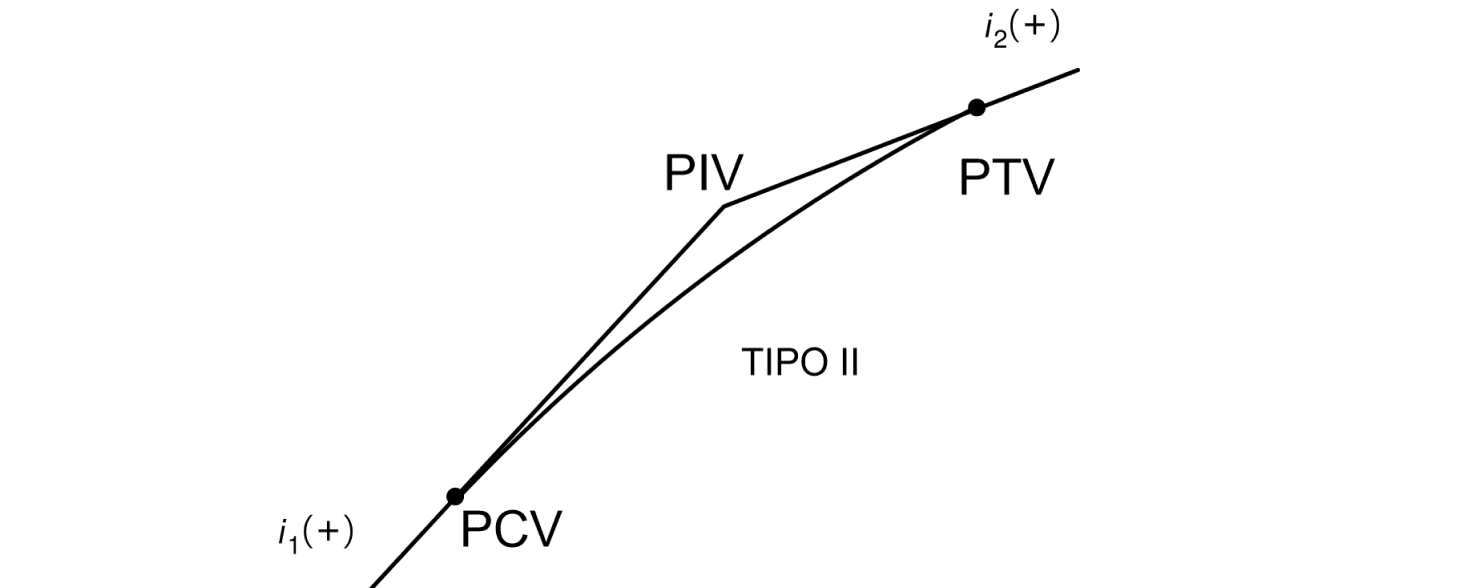
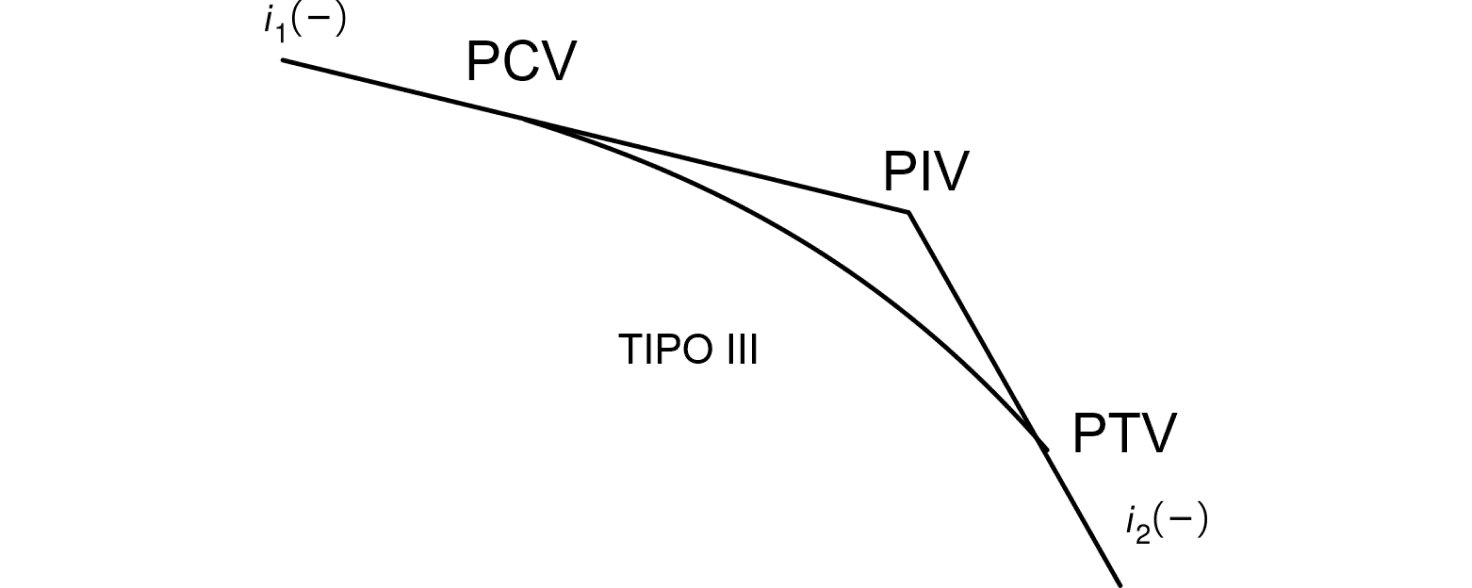
Curvas côncavas
Exemplos de curvas côncavas são:
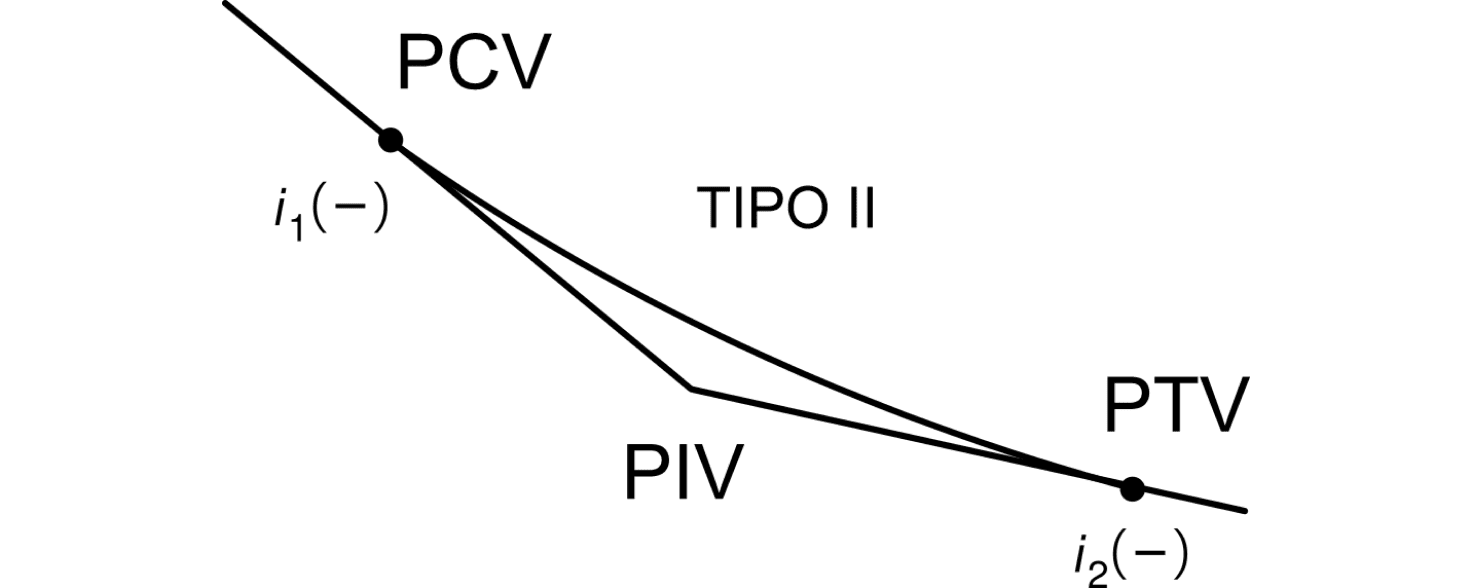
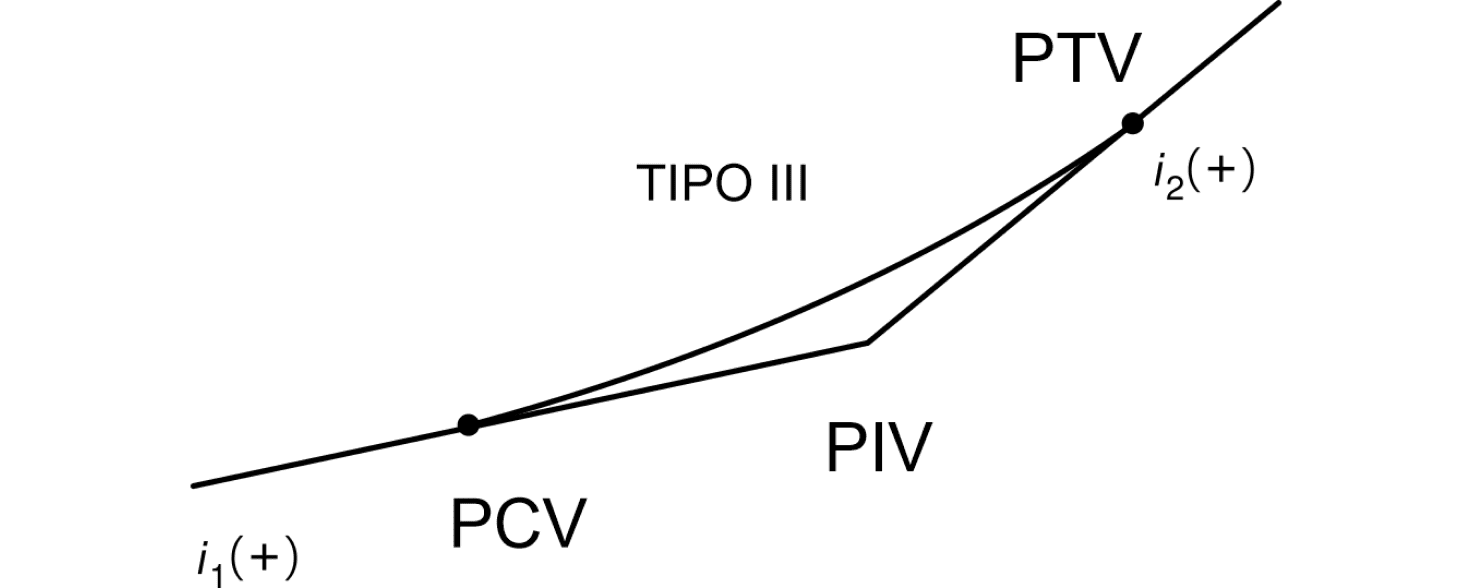
Atenção
Podem ser dispensadas curvas verticais quando a diferença algébrica entre rampas contíguas for inferior a 0,5%.
Curvas clássicas de concordância empregadas
São as seguintes:
- parábola de 2º grau;
- curva circular;
- elipse;
- parábola cúbica.
Os pontos notáveis de uma curva vertical são:
PCV
Chamado de ponto de curvatura vertical.
PIV
Chamado de ponto de inflexão vertical.
PTV
Chamado de ponto de tangência vertical.
O DNIT recomenda o uso de parábolas de 2° grau no cálculo de curvas verticais, de preferência simétricas em relação ao PIV, como mostrado na figura a seguir, em que a distância entre o PCV e o PIV, bem como entre o PIV e o PTV, sejam sempre iguais.
Parábola de 2º grau.
Flechas parciais da parábola
Em particular, no ponto PIV, temos a Flecha Máxima (F), que é a seguinte:
$$$ F=\frac{g}{2 L}\left(\frac{L}{2}\right)^{2}=\frac{g}{2 L} \cdot \frac{L^{2}}{4}=\frac{g L}{8} $$$
Que nada mais é que a equação da parábola a seguir, que tem o PCV na origem, aplicada quando x = L/2, ou seja, a distância horizontal do ponto de cálculo na metade da parábola, ou seja, x=L/2:
$$$ y=\frac{g}{2 L}(x)^{2} $$$
Esquema para cálculo de cotas e flechas da parábola.
Cálculo das estacas de uma parábola
Existem duas situações para calcular as estacas e as cotas de uma parábola simples, tendo como base a equação da parábola anteriormente definida.
Estacas
Estaca PCV = Estaca PIV – (L/2)
Estaca PTV = Estaca PIV + (L/2)
Cotas
Cota PCV = Cota PIV – i1.(L/2)
Cota PTV = Cota PIV – i2.(L/2)
Em que:
- $$$i_1$$$ é a rampa do trecho entre o PCV e o PIV;
- $$$i_2$$$ é a rampa de trecho entre o PIV e o PTV.
(Adaptado de ANTAS et al, 2010) Dada a curva apresentada na figura a seguir, e sabendo que o raio vertical é de 3.000m, a cota ascendente $$$(i_1)$$$ é de 2% e a descendente $$$(i_2)$$$ é de - 6%, calcule o grau da curva, o comprimento da curva vertical, bem como as estacas e cotas do PCV e do PTV. Sabendo ainda que a cota do PIV é 830m, na estaca 80, o PCV está na estaca 74 e o PTV, na estaca 86.
Inicialmente, vamos calcular o grau da curva:
$$$g=i1-i2=0,02–(-0,06)=0,08>0, $$$
o que nos dá uma curva convexa.
Cálculo do comprimento da curva vertical (L): multiplica-se o grau da curva pelo raio vertical:
$$$L=3000\times0,080=240m$$$
Estaca do PCV: é calculada a partir da estaca do PIV, que está na estaca 80. Assim, temos que:
$$$\text{- Estaca}\;PCV=\text{Estaca}\;PIV-\left(\frac L2\right)=80-\left(\frac{240}2\right)m=80-120\;\mathrm m$$$ (mas 120 m corresponde a 6 estacas), então, a estaca do PCV é 74.
$$$\text{- Estaca }PTV=\text{Estaca }PIV+\left(\frac L2\right)=80+\left(\frac{240}2\right)m=80+120\;\mathrm m$$$ (mas 120 m corresponde a 6 estacas), então, a estaca do PCV é 86.
$$$\text{-Cota }PCV=\text{Cota }PIV-i_1\cdot\left(\frac L2\right)=830-0,02\cdot120=830-2,4=827,60\;\mathrm m$$$
$$$\text{-Cota}\;PTV=\text{Cota }PIV+i_1\cdot\left(\frac L2\right)=830-0,08\cdot120=830-7,2=822,80\;\mathrm m$$$
cálculo de uma concordância vertical
Se considerarmos a planta e o perfil de uma rodovia, como acabamos de estudar, nem sempre conseguiremos identificar o tipo e a classificação da via.
É só percebermos duas rodovias, por exemplo:
BR-230
Corta a Amazônia.
BR-116
Corta inúmeros estados brasileiros.
Os dois trechos possuem curvas horizontais e verticais, greides, tangentes, superelevações e superlarguras em suas curvas.
A grande diferença que pode ser estabelecida está na chamada seção transversal.
Mas você sabe o que é uma seção transversal? É o que estudaremos neste módulo.
Seção transversal é a representação geométrica, no plano vertical, de alguns elementos dispostos de forma transversal ao eixo longitudinal da rodovia. Assim como os eixos longitudinais, podem ser seções transversais do terreno ou da estrada.
Seção transversal do terreno
(ou perfil transversal do terreno)
É a representação, no plano vertical, das diferenças de nível, obtidas do resultado de um nivelamento, normal em cada estaca, pertencente ao alinhamento da estrada.
Seção transversal da estrada
(ou perfil transversal da estrada)
É a representação geométrica, no plano vertical, de alguns elementos dispostos transversalmente, em determinado ponto do eixo longitudinal da estrada. Poderemos ter seção em corte, seção em aterro ou seção mista.
Tipos de seção transversal
Podem ser de três tipos: seção em corte, seção em aterro e seção mista, conforme pode ser visto a seguir.
Quando o projeto da rodovia resulta em uma estrada abaixo da superfície determinada pelo terreno natural.
Seção em corte
Quando o projeto da rodovia resulta em uma estrada acima da superfície determinada pelo terreno natural.
Seção em aterro
Quando o projeto da rodovia resulta, de um lado, uma estrada acima da superfície determinada pelo terreno natural e, por outro lado, uma estrada abaixo da superfície do terreno.
Seção mista
Elementos de uma seção transversal
Os elementos da seção transversal têm influência sobre suas características operacionais, estéticas e de segurança. Devem ser adequados aos padrões estabelecidos de velocidade, capacidade de tráfego, nível de serviço, aparência e segurança, sendo condicionados à largura e ao número de faixas de rolamento, aos acostamentos, ao canteiro central e aos taludes.
A seguir, temos dois exemplos de como seções transversais podem se apresentar.
Seção transversal típica de pista simples
Seção transversal típica de pista dupla
Pista de rolamento
Destina-se ao deslocamento dos veículos rodoviários. Como os veículos normalmente se deslocam em fila, em sentidos opostos e com movimento contínuo, a pista de rolamento contém, no mínimo, duas faixas de tráfego, sendo cada uma delas em um sentido, típico da pista simples. A faixa de tráfego deve ser capaz de conter a largura do veículo, acrescida de folgas laterais, para permitir que os veículos circulem de forma segura.
A largura da faixa de rolamento será função do veículo de projeto e da velocidade diretriz. As normas internacionais adotam como largura padrão 3,60m para faixa de rolamento, estabelecendo uma variação e 3,00 a 3,75m, conforme as velocidades consideradas.
A Tabela a seguir mostra as larguras recomendadas pelo DNIT para faixas de rolamento em pista de tangente para cada classe da rodovia.
| Classe da rodovia | Região plana | Região ondulada | Região montanhosa |
|---|---|---|---|
| 0 | 3,60 | 3,60 | 3,60 |
| I | 3,60 | 3,60 | 3,50 |
| II | 3,60 | 3,50 | 3,30 – 3,50 |
| III | 3,50 | 3,30 – 3,50 | 3,30 |
| IV-A | 3,00 | 3,00 | 3,00 |
| IV-B | 2,50 | 2,50 | 2,50 |
Tabela: Larguras das faixas de rolamento
(m).
Extraído de Manual de projeto geométrico de rodovias vicinais, DNIT.
Como saber o número mais adequado de faixas necessárias para a via?
Faça um estudo de capacidade em função do volume de tráfego ao longo da vida útil da rodovia. No mínimo, deve haver a via simples, uma para cada sentido.
Outro aspecto importante em uma pista é o chamado abaulamento, uma inclinação transversal para ambos os lados que permite uma melhora no escoamento das águas das chuvas.
A recomendação é adotar os valores a seguir, de acordo com a superfície do pavimento presente na rodovia:
- Pavimento de concreto de cimento: 1% ou, de preferência, 1,5%;
- Concreto betuminoso usinado a quente: 2%;
- Pavimento asfáltico poroso, como macadame betuminoso, tratamento superficial etc.: 2,5% a 3%;
- Revestimento primário: 3 a 4%.
Acostamento
São faixas que ladeiam as pistas de rolamento. Geralmente, proporcionam estacionamento, repouso, suporte lateral para veículos e até mesmo o tráfego de pedestres, bicicletas ou mesmo veículos de tração animal. Trata-se de um elemento de seção transversal imprescindível para a segurança de tráfego.
Dica
Da mesma forma que a faixa de rolamento, o valor desejável para a largura do acostamento será função da velocidade diretriz e do volume do tráfego.
Condição ideal de largura do acostamento é aquela que prevê espaço apenas para estacionamento do veículo de projeto, mantendo um aspecto contrastante, de alguma forma, com a pista de rolamento.
A tabela a seguir mostra as larguras recomendadas pelo DNIT para faixas de acostamento, em pista de tangente, para cada classe da rodovia.
| Classe da rodovia | Região plana | Região ondulada | Região montanhosa |
|---|---|---|---|
| 0 | 3,50 | 3,00 – 3,50 | 3,00 – 3,50 |
| I | 3,00 – 3,50 | 2,50 | 2,50 |
| II | 2,50 | 2,50 | 2,50 |
| III | 2,50 | 2,00 | 1,50 |
| IV-A | 1,30 | 1,30 | 0,80 |
| IV-B | 1,00 | 1,00 | 0,50 |
Tabela: Largura das faixas de acostamento
(m).
Extraída de Manual de projeto geométrico de rodovias vicinais, DNIT.
Elementos de drenagem
Têm como objetivo a condução no sentido longitudinal das águas para que sejam lançadas no terreno natural.
Exemplo
O exemplo mais comum é a sarjeta, cuja seção faz parte da seção transversal da rodovia.
Os elementos de drenagem podem ter forma retangular, triangular ou trapezoidal. Caberá ao projeto de drenagem a verificação da seção necessária que atenda ao escoamento das águas da rodovia.
Os tipos de revestimentos mais recomendados são:
- Concreto;
- Alvenaria de tijolo ou de pedra;
- Pedra arrumada;
- Vegetação.
Podem ainda ter cobertura de grama ou serem construídas de concreto simples, dependendo da velocidade de escoamento e do tipo de solo. Terrenos permeáveis ou fluxos de água com altas velocidades ensejam sempre seu revestimento com concreto simples.
A seguir, você vai conhecer alguns tipos de sarjetas trapezoidais e triangulares.
Valetas de proteção de aterro
Nas imagens a seguir, é possível ver dois exemplos de valetas de proteção de aterro.
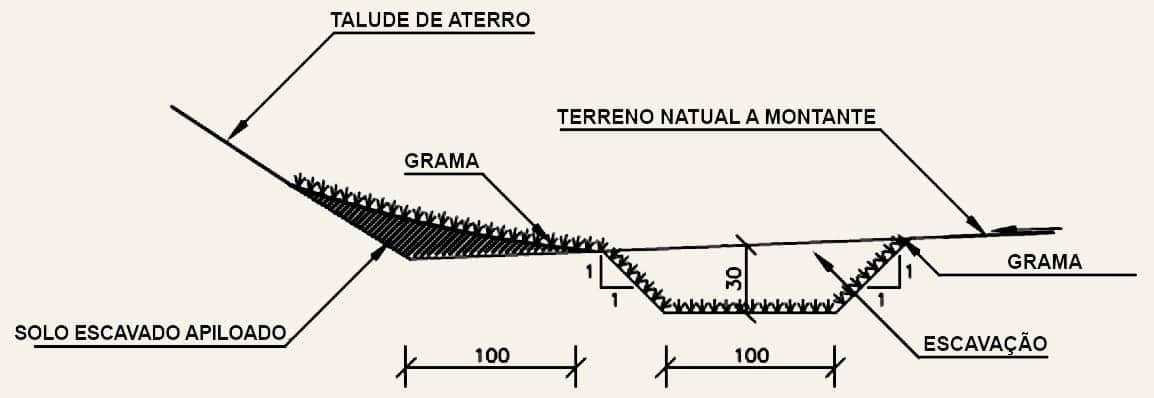
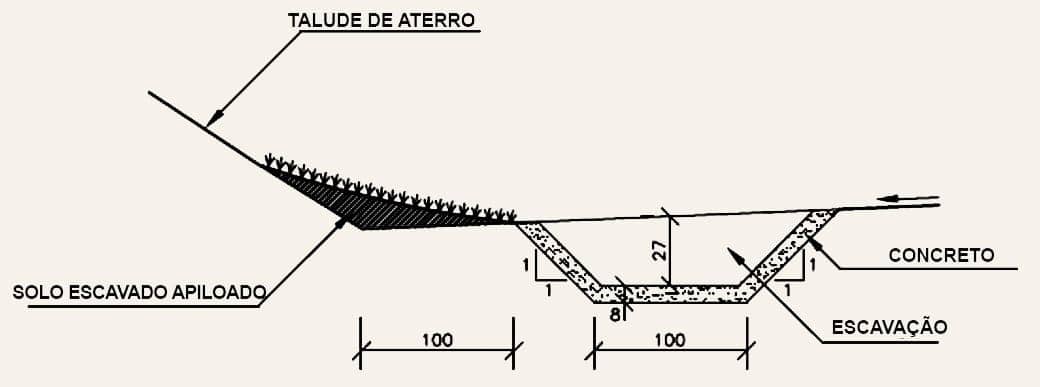
Sarjetas de pé-de-corte
Nas imagens a seguir, é possível ver dois exemplos de sarjetas de pé-de-corte, para proteção de taludes de corte.
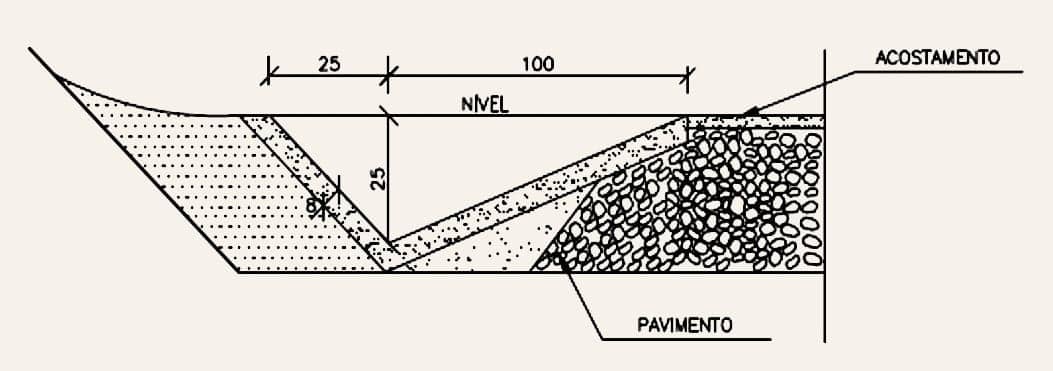
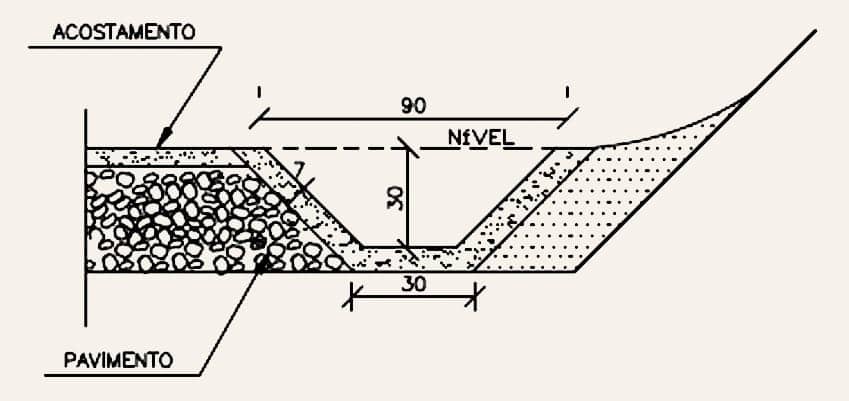
Talude
Formam o contorno lateral do corpo da estrada. Podem ser realizados em rocha ou em solo, e sua construção deve ser objeto de um cuidadoso estudo de estabilidade, de forma a buscar a melhor solução para sua construção.
Parte da preocupação do engenheiro geotécnico é a definição da inclinação desses taludes.
Em uma seção transversal, o ponto mais alto dos taludes é chamado de crista, e o ponto mais baixo, de pé. Taludes muito elevados são normalmente compartimentados a fim de reduzir os efeitos da erosão causada pelo deslocamento das águas.
A seguir, temos algumas inclinações sugeridas para taludes em rocha e em solo:
Inclinação de 1H:1V, ou seja, um metro na horizontal para um na vertical, correspondendo a um ângulo de 45°.
Inclinação de 1H:8V, ou seja, um metro na horizontal para oito na vertical.
Inclinação de 1,5H:1V a 2H:1V, ou seja, 1,5 a 2 metros na horizontal para um na vertical.
inclinação de 4H:1V, ou seja, quatro metros na horizontal para um na vertical.
Previstas em pistas duplas, têm a função de separar fisicamente as correntes de tráfego de sentidos opostos, o que pode ocorrer por meio de um canteiro central ou por separador físico contínuo, para prover segurança ao usuário, ao se evitar o choque de veículos em sentidos opostos. No caso do canteiro central, pode possuir uma largura de, no mínimo, 6 a 7 metros, sendo uma largura ideal entre 10 a 12 metros.
Espaços criados na rodovia compreendidos entre os limites externos dos passeios ou entre os pés-de-cortes e as cristas dos aterros.
Também podem ser citados como elementos:
Defensas e barreiras
Estruturas acessórias colocadas próximas aos bordos das plataformas de pistas simples com o fim de conter veículos desgovernados que possam sair da plataforma.

Defensas
São estruturas rígidas ou deformáveis, conforme o projeto.

Barreiras
São geralmente muros contínuos de concreto usados como separadores centrais em pistas duplas.
Gabarito
Porção no espaço dentro da rodovia em que não deve haver qualquer impedimento de obstáculos ao deslocamento de veículos.
Geralmente, o gabarito vertical mínimo desejável é de 5,50m e o absoluto pode variar entre 5,50 e 4,50m.
Faixa de domínio
Define a área pertencente à rodovia, sendo estabelecida com a previsão de uma futura duplicação. Pressupõe-se uma folga de 10m além da crista dos cortes e dos pés dos aterros.
O cálculo de áreas é muito útil para o desenvolvimento do projeto de terraplenagem, pois dele define-se os volumes de um trecho da rodovia.
Existem vários métodos de cálculo:
Método geométrico
Dividindo a seção transversal em figuras geométricas conhecidas.
Método analítico
Usando fórmulas, em que não se consideram a superelevação e a superlargura.
Processo mecânico
Por meio do planímetro.
Processo computacional
Com o auxílio de programas como o Civil 3D e o AutoCAD.
Vamos estudar, então, o método analítico simplificado: Embora o processo simplificado leve a erros por admitir o terreno em nível, é um processo usado, pois nos permite avaliar com rapidez os volumes de terraplanagem.
Método de cálculo analítico simplificado.
$$$ A=b \cdot h+n \cdot h^{2} $$$
Em que:
- $$$b$$$ e $$$h$$$ são as dimensões do trapézio;
- $$$n$$$ é a inclinação do talude (n/1).
Para a seção de corte, adota-se entre n=2/3 a n=1; para a seção de aterro, n=3/2.
Uma rodovia classe II de duas faixas, plana, com acostamentos nos dois sentidos e folga de 40cm de cada lado para a instalação de uma sarjeta, é construída sobre aterro. A altura média do aterro é de 2m. Calcule o volume de terraplenagem por cada quilômetro dessa rodovia se a seção transversal ao longo de uma estaca é como mostra a imagem a seguir:
Cálculo de um volume de terraplenagem
Neste conteúdo, conhecemos os processos de projeto geométrico de rodovias.
No primeiro módulo, identificamos e reconhecemos os elementos geométricos planimétricos de uma rodovia: curvas circulares simples e de transição, tangentes e elementos do traçado horizontal.
No segundo módulo, identificamos e reconhecemos e superelevação e superlargura de uma rodovia, calculando-as e aplicando-as em um traçado.
No terceiro módulo, identificamos e reconhecemos os elementos geométricos altimétricos de uma rodovia: greides retos e curvas verticais parabólicas.
No último módulo, conhecemos as seções transversais mais comuns no projeto geométrico de rodovias, conhecendo as formas mais simples de calcular sua área.
Com tais conhecimentos, você terá todas as condições necessárias para continuar o seu estudo de projeto de rodovias.
Agora, o especialista Giuseppe Miceli Junior encerra o tema falando sobre os principais tópicos abordados.